The Virtues of Complex Models
發布時(shí)間:2023-08-07 | 來(lái)源: 川總寫量化(huà)
摘要:跟著(zhe)兩位大(dà)佬一起洞悉金融機器學習(xí)的(de)最新學術前沿(II)。
作者:石川
上期公衆号翻譯了(le) Bryan Kelly 和(hé)修大(dà)成兩位教授最新的(de) Financial Machine Learning 的(de)第一章(zhāng)。之後有小夥伴催更後續章(zhāng)節。
該文的(de)第二章(zhāng)标題爲 The Virtues of Complex Models,即複雜(zá)模型的(de)好處。公衆号的(de)老朋友也(yě)許在最近一年以來(lái)對(duì)這(zhè)個(gè)提法不再陌生。Bryan Kelly 這(zhè)兩年一個(gè)重要的(de) research agenda 就是 The Virtues of Complexity 系列,而我也(yě)很早就開始追蹤他(tā)在這(zhè)方面的(de)研究成果并通(tōng)過公衆号多(duō)次進行了(le)非 technical 的(de)介紹(例如《機器學習(xí)與資産定價:Facts and Fictions》以及《因子投資的(de)高(gāo)維數時(shí)代》)。因此,雖然不敢說對(duì)這(zhè)章(zhāng)的(de)内容如數家珍,但也(yě)算(suàn)是比較熟悉。更重要的(de)是,我也(yě)越來(lái)越意識到 The Virtues of Complexity 對(duì)于量化(huà)投資和(hé)因子投資的(de)啓示。
因此,今天繼續翻譯 Financial Machine Learning 的(de)第二章(zhāng)。再次感謝劉洋溢和(hé)王熙兩位老師提出的(de)寶貴修改建議(yì)。
最後,本翻譯僅供學習(xí)交流使用(yòng),禁止一切商業行爲,未經授權,禁止轉載。
以下(xià)是正文部分(fēn)。
包括我們在内的(de)許多(duō)人(rén)在接受計量經濟學培訓時(shí),都承襲了(le)“簡約原則”這(zhè)一傳統。該原則充分(fēn)地體現在 Box and Jenkins (1970) 的(de)模型建立方法中,對(duì)金融計量經濟學産生了(le)深遠(yuǎn)的(de)影(yǐng)響。在 Box 和(hé) Jenkins 兩位關于預測的(de)最新版教科書(shū)的(de)引言中,“構建模型的(de)基本觀念”中的(de)第一條就是“簡約性”,他(tā)們強調“實踐中,我們應使用(yòng)盡可(kě)能少的(de)參數來(lái)準确地描述一個(gè)現象,過程或數據集的(de)性質或行爲,這(zhè)一點非常重要”。
在現代機器學習(xí)算(suàn)法采用(yòng)大(dà)規模參數化(huà)這(zhè)一現實面前,簡約模型似乎顯得(de)格格不入。領先的(de) GPT-3 語言模型(Brown et al. 2020)使用(yòng)了(le) 1750 億個(gè)參數。即使是 Gu, Kelly and Xiu (2020) 中那個(gè)在規模上完全不可(kě)與之相提并論的(de)收益率預測神經網絡模型也(yě)有差不多(duō) 30000 個(gè)參數。對(duì)于承襲 Box-Jenkins 的(de)計量經濟學家來(lái)說,如此豐富的(de)參數化(huà)似乎過于奢侈,容易導緻過拟合,并可(kě)能在樣本外産生災難性的(de)表現。
然而,近年來(lái)在許多(duō)金融之外其他(tā)領域的(de)研究成果均與上述觀點相悖。在計算(suàn)機視覺和(hé)自然語言處理(lǐ)等應用(yòng)中,擁有海量參數的(de)模型,以及完美(měi)拟合訓練集樣本的(de)模型,通(tōng)常正是樣本外表現最好的(de)模型(譯者注:不過人(rén)工智能文獻也(yě)往往擁有較大(dà)的(de)數據集、并擁有諸多(duō)數據加強的(de)方法)。在概括神經網絡文獻的(de)現狀時(shí),Belkin (2021) 總結到:“從技術可(kě)行性的(de)角度看,最複雜(zá)的(de)網絡總是能産生最優異的(de)表現。”顯然,現代機器學習(xí)研究颠覆了(le)計量經濟學所奉行的(de)簡約原則。
人(rén)們試圖爲解釋大(dà)規模參數化(huà)的(de)成功尋求理(lǐ)論基礎,并回答(dá) Breiman (1995) 提出的(de)問題:“爲什(shén)麽參數衆多(duō)的(de)神經網絡沒有過度拟合數據?”在本節中,我們将一窺這(zhè)個(gè)問題的(de)答(dá)案。爲此,我們借鑒了(le)統計文獻中的(de)最新發現,它們描述了(le)“過度參數化(huà)”模型(即參數個(gè)數遠(yuǎn)超可(kě)用(yòng)訓練集的(de)觀測數據個(gè)數)的(de)行爲。
最新的(de)文獻已經開始回答(dá)機器學習(xí)模型的(de)統計理(lǐ)論含義,并關注過度參數化(huà)模型的(de)樣本外預測準确性。在這(zhè)一章(zhāng),我們關注的(de)問題是金融機器學習(xí)中過度參數化(huà)以及過拟合現象所帶來(lái)的(de)經濟影(yǐng)響。已經有不少金融學論文發現,通(tōng)過機器學習(xí)模型能顯著提高(gāo)收益率預測的(de)準确性。收益率預測的(de)主要經濟用(yòng)途是構造效用(yòng)最優化(huà)的(de)投資組合。我們的(de)論述會側重于解釋“機器學習(xí)投資組合”在樣本外的(de)風險收益權衡,這(zhè)些投資組合通(tōng)過高(gāo)度參數化(huà)的(de)收益率預測模型而構造。我們的(de)論述主要基于 Kelly, Malamud and Zhou (2022a) 和(hé) Didisheim et al. (2023) 的(de)發現。
2.1 分(fēn)析機器學習(xí)模型的(de)工具
Kelly, Malamud and Zhou (2022a) 提出了(le)一個(gè)思想實驗。設想一位分(fēn)析師在尋找一個(gè)成功的(de)收益率預測模型。假設資産收益率
其中預測變量集
在上面這(zhè)個(gè)回歸模型中,每個(gè)特征都是原始特征的(de)某個(gè)事先選定的(de)非線性變換,即
最終,分(fēn)析師的(de)目标是估計下(xià)面這(zhè)個(gè)近似回歸模型
爲此,分(fēn)析師有
也(yě)許聽(tīng)上去令人(rén)驚訝,但 Kelly, Malamud and Zhou (2022a) 指出分(fēn)析師應該使用(yòng)其算(suàn)力約束下(xià)能夠實現的(de)最複雜(zá)的(de)近似模型。樣本外預測的(de)準确性和(hé)投資組合的(de)預期表現會随著(zhe)模型複雜(zá)度而遞增。爲了(le)得(de)出這(zhè)個(gè)答(dá)案,Kelly, Malamud and Zhou (2022a) 借助了(le)兩種關鍵的(de)數學工具來(lái)分(fēn)析複雜(zá)的(de)非線性(即機器學習(xí))模型。它們分(fēn)别是帶生成非線性特征(即上面的(de)
2.1.1 帶生成特征的(de)嶺回歸
Kelly, Malamud and Zhou (2022a) 的(de)第一個(gè)建模假設聚焦于式 (2.3) 所示的(de)高(gāo)維線性預測模型,我們稱之爲“實證模型”。關于式 (2.3) 的(de)正确理(lǐ)解爲,這(zhè)一公式并非強調收益率會受到爲數衆多(duō)的(de)驅動力的(de)線性影(yǐng)響。相反,它表明(míng)的(de)是數據生成過程(DGP)是未知的(de),但它或許可(kě)以通(tōng)過一組變量
這(zhè)個(gè)問題的(de)一個(gè)鮮明(míng)特點是,實證模型往往存在模型設定偏誤。在式 (2.3) 中消除模型設定偏誤需要我們無限地擴展模型所包含的(de)特征,但實際上我們隻能使用(yòng)有限個(gè)數的(de)特征,即
第二個(gè)建模假設是使用(yòng)嶺回歸作爲 (2.3) 的(de)估計量:
其中
最後,爲了(le)刻畫(huà)高(gāo)複雜(zá)度模型對(duì)于投資者的(de)經濟影(yǐng)響,Kelly, Malamud and Zhou (2022a) 假設投資者使用(yòng)預測結果按照(zhào)如下(xià)方式構造交易策略:
式中
盡管還(hái)存在其他(tā)合理(lǐ)的(de)策略構造方式以及績效評價标準,但上述選擇均是在學術界和(hé)投資業界中的(de)常見選擇,因此它們兼顧透明(míng)性和(hé)易理(lǐ)解性。
2.1.2 随機矩陣理(lǐ)論
上述嶺回歸公式以線性回歸的(de)方式展示了(le)像神經網絡這(zhè)樣的(de)機器學習(xí)模型。我們的(de)願景是,通(tōng)過這(zhè)種表示,可(kě)能能夠對(duì)複雜(zá)模型在
當
它是
換句話(huà)說,模型複雜(zá)度對(duì)于人(rén)們理(lǐ)解模型的(de)行爲至關重要。如果樣本數量
2.2 越大(dà)往往越好
Kelly, Malamud and Zhou (2022a) 爲高(gāo)複雜(zá)度機器學習(xí)模型及其相關交易策略的(de)性質提供了(le)嚴格的(de)理(lǐ)論陳述。在實證部分(fēn),他(tā)們通(tōng)過市場(chǎng)收益率的(de)預測問題(譯者注:擇時(shí)問題)研究了(le)複雜(zá)模型的(de)參數校準問題,而我們接下(xià)來(lái)的(de)論述将側重于他(tā)們關于該問題的(de)重要定性結果。具體來(lái)說,他(tā)們假設市場(chǎng)的(de)年波動率爲 20%,并假設當真實函數關系和(hé)預測變量對(duì)預測者完全已知時(shí),她所能取得(de)的(de)“真實”(但當然是無法實現的(de))月(yuè)頻(pín)預測性
在上述參數校準問題中,他(tā)們假設真實但未知 DGP 的(de)複雜(zá)度爲
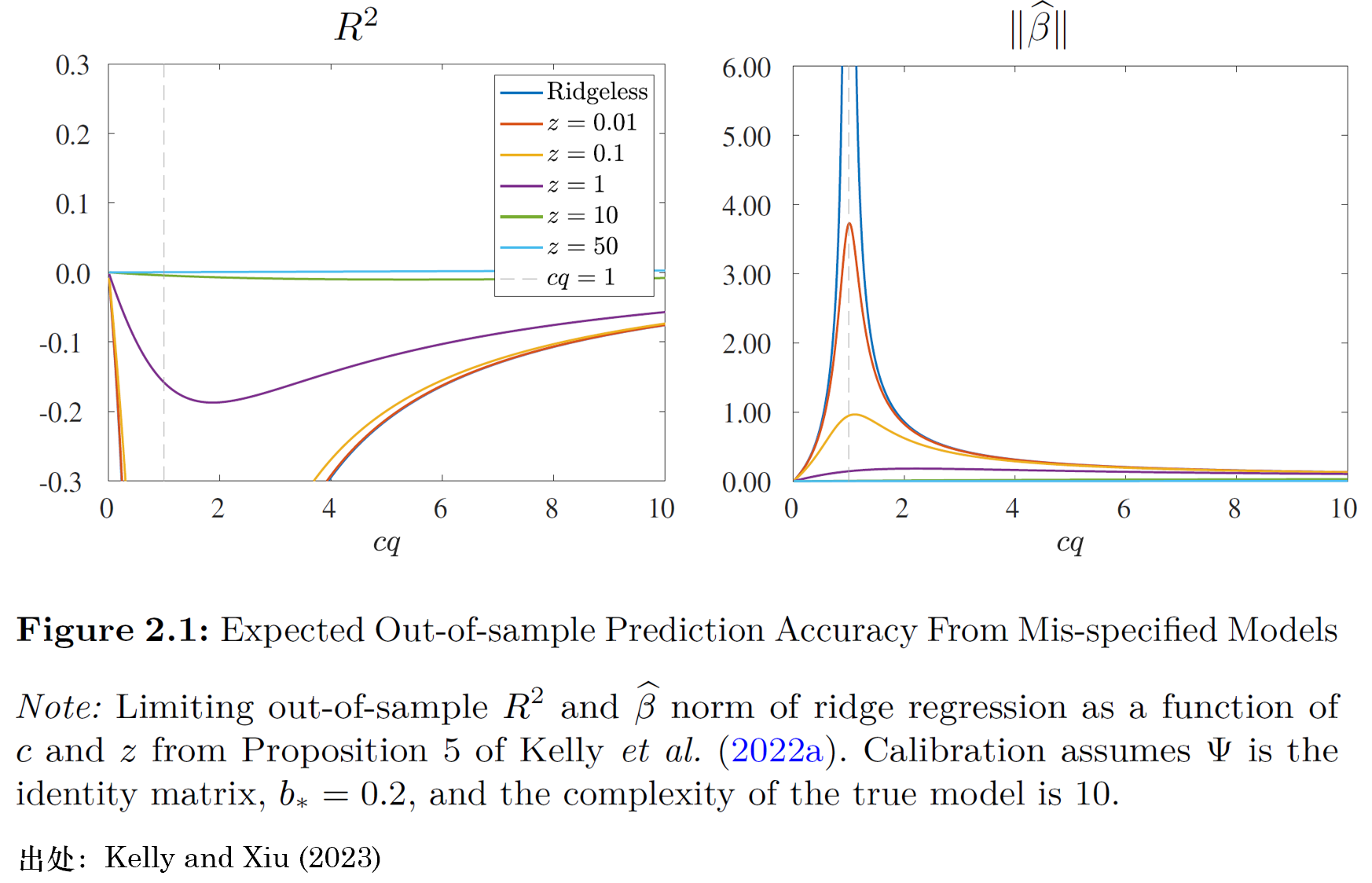
首先考慮普通(tōng)最小二乘法(OLS)估計量
當
令人(rén)驚訝的(de)是,當模型複雜(zá)度超過 1 時(shí)(譯者注:根據作者的(de)定義,這(zhè)對(duì)應
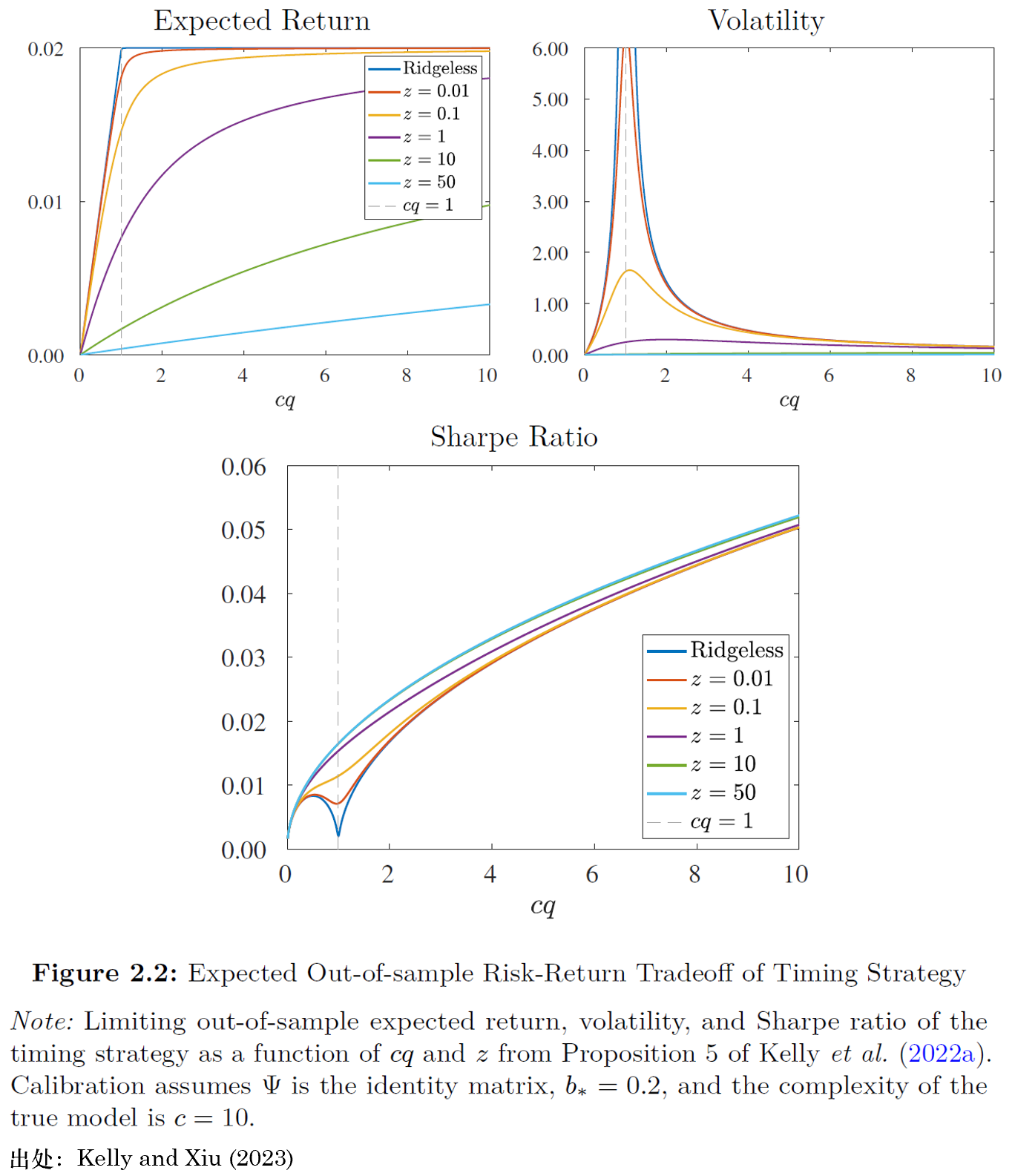
圖 2.1 描述了(le)高(gāo)複雜(zá)度模型的(de)統計行爲。圖 2.2 則将注意力轉向它們的(de)經濟後果。圖中第一行右側的(de)子圖展示了(le)機器學習(xí)交易策略的(de)波動率如何随模型複雜(zá)度變化(huà)。策略的(de)波動率與
圖 2.2 中第一行左側的(de)子圖則展示了(le)高(gāo)複雜(zá)度模型的(de)關鍵經濟行爲 —— 擇時(shí)策略在樣本外的(de)預期收益率。對(duì)簡單策略來(lái)說,它們的(de)預期收益率較低。同樣,這(zhè)是因爲簡單的(de)模型無法很好地近似真實的(de) DGP。增加模型的(de)複雜(zá)度可(kě)以使人(rén)們更接近真實情況,并且單調地提升交易策略的(de)預期收益率。
這(zhè)二者對(duì)投資者最終的(de)投資結果意味著(zhe)什(shén)麽?圖 2.2 第二行的(de)子圖以樣本外預期夏普比率爲例展示了(le)投資者的(de)效用(yòng)。樣本外夏普比率可(kě)歸結爲經典的(de)偏差-方差權衡。預期收益率純粹反映偏差影(yǐng)響。對(duì)于低複雜(zá)度模型而言,偏差來(lái)源于模型設定偏誤,而非對(duì)參數的(de)收縮作用(yòng)。對(duì)于高(gāo)複雜(zá)度模型,模型設定偏誤變小,但是參數收縮導緻的(de)偏差較大(dà)。理(lǐ)論顯示,預期收益率随模型複雜(zá)度而提升,這(zhè)意味著(zhe)對(duì)這(zhè)個(gè)預測問題而言,模型設定偏誤造成的(de)偏差比參數收縮造成的(de)偏差代價更大(dà)。與此同時(shí),策略的(de)波動率純粹由預測的(de)方差決定。無論是簡單模型(
我們可(kě)以将上述發現和(hé)“雙(側)下(xià)降”現象加以比較,“雙下(xià)降”現象指的(de)是當
總的(de)來(lái)說,這(zhè)些結果挑戰了(le)本節前言所討(tǎo)論的(de)簡約主義信仰。它們表明(míng),在實證模型存在模型設定偏誤的(de)情況下(xià),複雜(zá)度是一種優點。這(zhè)不僅對(duì)于樣本外的(de)統計表現而言是正确的(de)(如 Belkin et al. 2019;Hastie et al. 2019 等),而且對(duì)樣本外投資者的(de)經濟效用(yòng)而言也(yě)是正确的(de)。與傳統的(de)觀點相反,通(tōng)過讓模型參數個(gè)數遠(yuǎn)超過訓練集樣本個(gè)數,理(lǐ)論上可(kě)以提高(gāo)基于機器學習(xí)模型所構造的(de)投資組合的(de)(譯者注:樣本外)表現。
對(duì)于使用(yòng)複雜(zá)模型的(de)最佳實踐,Kelly, Malamud and Zhou (2022a) 總結到:
我們的(de)結果并不意味著(zhe)随意向模型中添加任意預測因子。相反,我們建議(yì):(1)模型包含所有可(kě)能相關的(de)預測因子,以及(2)使用(yòng)複雜(zá)的(de)非線性模型取代簡單的(de)線性模型。哪怕在訓練集數據稀缺的(de)情況下(xià),這(zhè)樣做(zuò)也(yě)會改進預測和(hé)投資組合,這(zhè)種作用(yòng)在配合謹慎的(de)參數收縮時(shí)更加明(míng)顯。
爲了(le)推導出上述結果,Kelly, Malamud and Zhou (2022a) 基于的(de)假設是可(kě)預測性在協變量之間均勻分(fēn)布。乍看上去,這(zhè)個(gè)假設或許過于苛刻,因爲許多(duō)标準的(de)預測變量都難以滿足這(zhè)一假設。然而,這(zhè)個(gè)假設與标準的(de)神經網絡模型是一緻的(de)(實際上也(yě)是由此引出的(de)),在這(zhè)種模型中,原始特征被混合并通(tōng)過非線性傳播進而彙聚到最終生成的(de)特征中,如式(2.2)所示。在訓練神經網絡的(de)初始化(huà)步驟中,生成特征 S 的(de)順序會被随機打亂。此外,在實證研究中,Kelly, Malamud and Zhou (2022a, 2022b) 以及 Didisheim et al. (2023) 使用(yòng)了(le)一種被稱爲随機特征回歸的(de)神經網絡形式,從而确保滿足這(zhè)一假設。
2.3 複雜(zá)度(造成的(de))鴻溝
Didisheim et al. (2023) 從不同角度對(duì) Kelly, Malamud and Zhou (2022a) 進行了(le)擴展,并提出了(le)“複雜(zá)度鴻溝”的(de)概念,它被定義爲樣本内和(hé)樣本外表現的(de)期望差異(譯者注:難以逾越的(de)差異)。簡單來(lái)說,考慮實證模型不存在設定偏誤問題。在低複雜(zá)度(
但當
對(duì)于資産定價而言,複雜(zá)度鴻溝有一些重要的(de)啓示。對(duì)于已實現的(de)(可(kě)行的(de))預測
Da, Nagel and Xiu (2022) 考慮了(le)一個(gè)特殊的(de)經濟環境,其中的(de)經濟主體(即套利者)采用(yòng)統計套利策略并試圖最大(dà)化(huà)他(tā)們樣本外的(de)夏普比率。這(zhè)些套利者在學習(xí) alpha 的(de)數據生成過程時(shí)也(yě)面臨統計難題(和(hé)上述“複雜(zá)度”類似)。Da, Nagel and Xiu (2022) 顯示,在特定的(de)低信噪比環境下(xià),無論套利者使用(yòng)哪種機器學習(xí)方法,他(tā)們都無法獲得(de)最優的(de)夏普比率(無法實現的(de))(譯者注:即套利者無法準确習(xí)得(de) DGP)。此外,即使套利者采用(yòng)最優的(de)可(kě)行交易策略,他(tā)們所獲得(de)的(de)夏普比率與最優(但無法實現)的(de)夏普比率之間仍然存在巨大(dà)的(de)差距。我們将在第 4.6 章(zhāng)中進一步討(tǎo)論上述論文的(de)細節。
參考文獻
Belkin, M. (2021). Fit without fear: remarkable mathematical phenomena of deep learning through the prism of interpolation. Acta Numerica 30, 203–248.
Belkin, M., D. Hsu, S. Ma, and S. Mandal (2018). Reconciling modern machine learning and the biasvariance trade-off. arXiv e-prints.
Box, G. E. and G. Jenkins (1970). Time Series Analysis: Forecasting and Control. San Francisco: Holden-Day.
Breiman, L. (1995). The mathematics of generalization. In: CRC Press. Chap. Reflections After Refereeing Papers for NIPS. 11–15.
Brown, T., B. Mann, N. Ryder, M. Subbiah, J. D. Kaplan, P. Dhariwal, A. Neelakantan, P. Shyam, G. Sastry, A. Askell, S. Agarwal, A. Herbert-Voss, G. Krueger, T. Henighan, R. Child, A. Ramesh, D. Ziegler, J. Wu, C. Winter, C. Hesse, M. Chen, E. Sigler, M. Litwin, S. Gray, B. Chess, J. Clark, C. Berner, S. McCandlish, A. Radford, I. Sutskever, and D. Amodei (2020). Language models are few-shot learners. In: Advances in Neural Information Processing Systems. Ed. by H. Larochelle, M. Ranzato, R. Hadsell, M. Balcan, and H. Lin. Vol. 33. Curran Associates, Inc. 1877–1901.
Da, R., S. Nagel, and D. Xiu (2022). The statistical limit of arbitrage. Working paper.
Didisheim, A., S. Ke, B. T. Kelly, and S. Malamud. (2023). Complexity in factor pricing models. Working paper.
Gu, S., B. T. Kelly, and D. Xiu (2020). Empirical asset pricing via machine learning. Review of Financial Studies 33(5), 2223–2273.
Hastie, T., A. Montanari, S. Rosset, and R. J. Tibshirani (2019). Surprises in high-dimensional ridgeless least squares interpolation. arXiv preprint arXiv:1903.08560.
Hornik, K., M. Stinchcombe, and H. White (1990). Universal approximation of an unknown mapping and its derivatives using multilayer feedforward networks. Neural Networks 3(5), 551–560.
Kelly, B. T., S. Malamud, and K. Zhou. (2022a). Virtue of complexity in return prediction. Working paper.
Kelly, B. T., S. Malamud, and K. Zhou. (2022b). The virtue of complexity everywhere. Working paper.
免責聲明(míng):入市有風險,投資需謹慎。在任何情況下(xià),本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià),本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外,文中圖表均直接或間接來(lái)自于相應論文,僅爲介紹之用(yòng),版權歸原作者和(hé)期刊所有。