Augmented Fama-MacBeth Regression

發布時(shí)間：2023-06-05 | 來(lái)源: 川總寫量化(huà)

作者：石川

摘要：增強版 Fama-MacBeth Regression 是研究 nontradable factor 的(de)利器。

因子有 tradable factors 和(hé) nontradable factors 之分(fēn)。對(duì)于前者而言，常見的(de)做(zuò)法是直接用(yòng)公司特征構造 managed portfolios；而對(duì)于後者，Fama-MacBeth two-pass regression 往往是首選，即在第一步中在時(shí)序上用(yòng)資産（超額）收益率對(duì)因子取值回歸來(lái)估計 $\beta$ ，第二步中每期在截面上用(yòng)資産（超額）收益率對(duì) $\beta$ 回歸估計因子 risk premia 和(hé)資産的(de) pricing errors。令 $\beta_{i,t-1}$ 表示 $t-1$ 期資産 $i$ 的(de)因子暴露向量， $r_{i,t}$ 表示 $t$ 期資産 $i$ 的(de)超額收益率，則上述第二步截面回歸模型可(kě)以表示爲（爲了(le)簡化(huà)符号，假設不帶截距項）：

$\displaystyle r_{i,t}=\beta_{i,t-1}^\prime f_t+\alpha_{i,t}$

式中 $f_t$ 爲 $t$ 期因子收益率向量，殘差 $\alpha_{i,t}$ 則爲資産 $i$ 的(de) pricing error。按照(zhào)傳統做(zuò)法，隻需在每期 $t$ 進行截面回歸，然後就可(kě)以對(duì) $f_i$ 和(hé) $\alpha_{i,t}$ 進行相應的(de)檢驗。故事到此似乎就結束了(le)。不過，既然本文的(de)題目帶個(gè)“augmented”，下(xià)面我們就來(lái)看看上述過程有什(shén)麽痛點。

在上述過程中，如果 nontradable factors 數量衆多(duō)（比如遠(yuǎn)遠(yuǎn)超過 ad-hoc 模型中通(tōng)常使用(yòng)的(de) 3 – 5 個(gè)因子）且高(gāo)度相關，那麽回歸估計就會有巨大(dà)的(de)誤差。因此，一個(gè)自然的(de)想法就是對(duì)因子進行降維處理(lǐ)。這(zhè)時(shí)，我們便可(kě)以請出這(zhè)幾年非常火的(de) IPCA（工具變量 PCA）方法（Kelly, Pruitt, and Su 2019）。該方法将 $\beta$ 視爲原始（高(gāo)維）協變量的(de)線性組合，即：

$\displaystyle\beta_{i,t}=\Gamma c_{i,t}$

其中 $L\times 1$ 維向量 $c_{i,t}$ 表示 $t$ 期資産 $i$ 在 $L$ 個(gè)原始高(gāo)維協變量（工具變量）的(de)取值， $\Gamma$ 是 $K\times L$ 維矩陣，将原始工具變量通(tōng)過 $K$ 個(gè)線性組合降爲到 $K$ 個(gè)因子，得(de)到資産 $i$ 對(duì) $K$ 個(gè)因子的(de)暴露向量 $\beta_{i,t}$ 。加入 IPCA 之後，Fama-MacBeth 第二步的(de)截面回歸變爲

$\displaystyle r_{i,t}=(\Gamma c_{i,t-1})^\prime f_t+\alpha_{i,t}$

在實際應用(yòng)中， $c_{i,t}$ 已知。我們可(kě)以通(tōng)過最小化(huà)所有資産的(de) pricing errors 來(lái)估計 $\Gamma$ 。在上述目标下(xià)，最優化(huà)問題的(de)目标函數等價于

$\displaystyle\min_{\Gamma, \left\{f_t\right\}}\frac{1}{2}\sum_{i,t}\left(r_{i,t}-(\Gamma c_{i,t-1})^\prime f_t \right)^2$

值得(de)一提的(de)是，雖然上述最優化(huà)問題中的(de)變量包括 $\Gamma$ 和(hé)每期的(de) $f_t$ 。但是，一旦給定 $\Gamma$ ， $\beta$ 實際上就确定了(le)，而一旦 $\beta$ 确定了(le)，使得(de) pricing errors 最小的(de)因子收益率 $f_t$ 自然而然就得(de)到了(le)。上述邏輯保證了(le) $\Gamma$ 和(hé) $f_t$ 之間内在的(de) economic connection。那麽至此，我們是否 augmented 完了(le)呢(ne)？（Hint：既然問了(le)，當然還(hái)沒有。）

在第二節中，我們将 IPCA 加入到 Fama-MacBeth 中，将原始 $L$ 個(gè)工具變量通(tōng)過 $K$ 個(gè)線性組合轉化(huà)成 $K$ 個(gè)因子，從而實現了(le)降維。但是從數學表達式中不難看出，每個(gè)因子都是 $L$ 個(gè)變量的(de)某種組合。在現實中， $L$ 很可(kě)能是高(gāo)維的(de)（幾百甚至上千），而我們雖然指望數據發聲，但同時(shí)有先驗告訴我們 $L$ 中的(de)某些工具變量和(hé) $\beta$ 沒什(shén)麽關系，因此在 $\Gamma$ 中不應該發揮作用(yòng)（即對(duì)應的(de)列應該都是元素零）。在這(zhè)樣的(de)背景下(xià)，我們希望在構造 $\Gamma$ 的(de)時(shí)候，引入稀疏性（sparsity），得(de)到 Sparse IPCA。

爲此，在估計 $\Gamma$ （以及 $f_t$ ）的(de)時(shí)候加入罰項：

$\displaystyle\min_{\Gamma, \left\{f_t\right\}}\frac{1}{2}\sum_{i,t}\left(r_{i,t}-(\Gamma c_{i,t-1})^\prime f_t \right)^2+\lambda\sum_{l=1}^L\lVert\Gamma_l\rVert_2+\sum_t\lVert f_t\rVert_2^2$

式中 $\Gamma_l$ 表示 $\Gamma$ 的(de)第 $l$ 列，且

$\displaystyle\lVert\Gamma_l\rVert_2=\sqrt{\Gamma_{1,l}^2+\Gamma_{2,l}^2+\cdots+\Gamma_{K,l}^2}$

目标函數中第一個(gè)罰項（式中第二項）可(kě)理(lǐ)解爲 column-wise group lasso。如果第 $l$ 個(gè)工具變量對(duì)估計 $\beta$ 沒有幫助，那麽 $\Gamma$ 中的(de)第 $l$ 列将會爲零。目标函數中的(de)第二個(gè)罰項（式中第三項）是出于技術方面的(de)考慮而加上的(de)。注意，目标函數中的(de)第一項是 pricing errors，在縮放 $\Gamma$ 時(shí)，我們總能通(tōng)過擴大(dà) $f_t$ 來(lái)保證第一項不變。因此，如果目标函數中沒有第二個(gè)罰項，那麽将會出現這(zhè)樣的(de)結果，即在不改變 pricing errors 的(de)前提下(xià) $\Gamma$ 将會變得(de)非常小從而使正則化(huà)失去本來(lái)的(de)作用(yòng)。目标函數中置于 $f_t$ 的(de)罰項正是爲了(le)避免上述情況發生而出現。最後，由于加入了(le)罰項，我們需要對(duì)超參數 $\lambda$ 調優。對(duì)于每個(gè)給定的(de) $\lambda$ ，求解最優化(huà)問題可(kě)得(de)到對(duì)應的(de) $\Gamma$ 和(hé) $f_t$ 時(shí)序。由資産定價理(lǐ)論可(kě)知，因子構造的(de) OOS 夏普比率平方應該盡可(kě)能大(dà)，而夏普比率可(kě)以表示爲：

$\displaystyle\sqrt{\mu_f^\prime\Sigma_f\mu_f}$

其中 $\mu_f$ 是因子預期收益率， $\Sigma_f$ 是因子協方差矩陣，它們均可(kě)通(tōng)過因子收益率時(shí)序估計得(de)到。因此可(kě)以以此爲目标确定最優的(de) $\lambda$ 。

Okay！以上就完成了(le)“augmented”部分(fēn)的(de)介紹。即我們從 Fama-MacBeth two-pass regression 出發，首先加入了(le) IPCA 實現了(le)降維，然後又在 IPCA 基礎上進而使用(yòng) Sparse IPCA 從而确保聚焦于隻和(hé) $\beta$ 有關的(de)變量，最後通(tōng)過經濟學理(lǐ)論爲依據進行超參數調優。

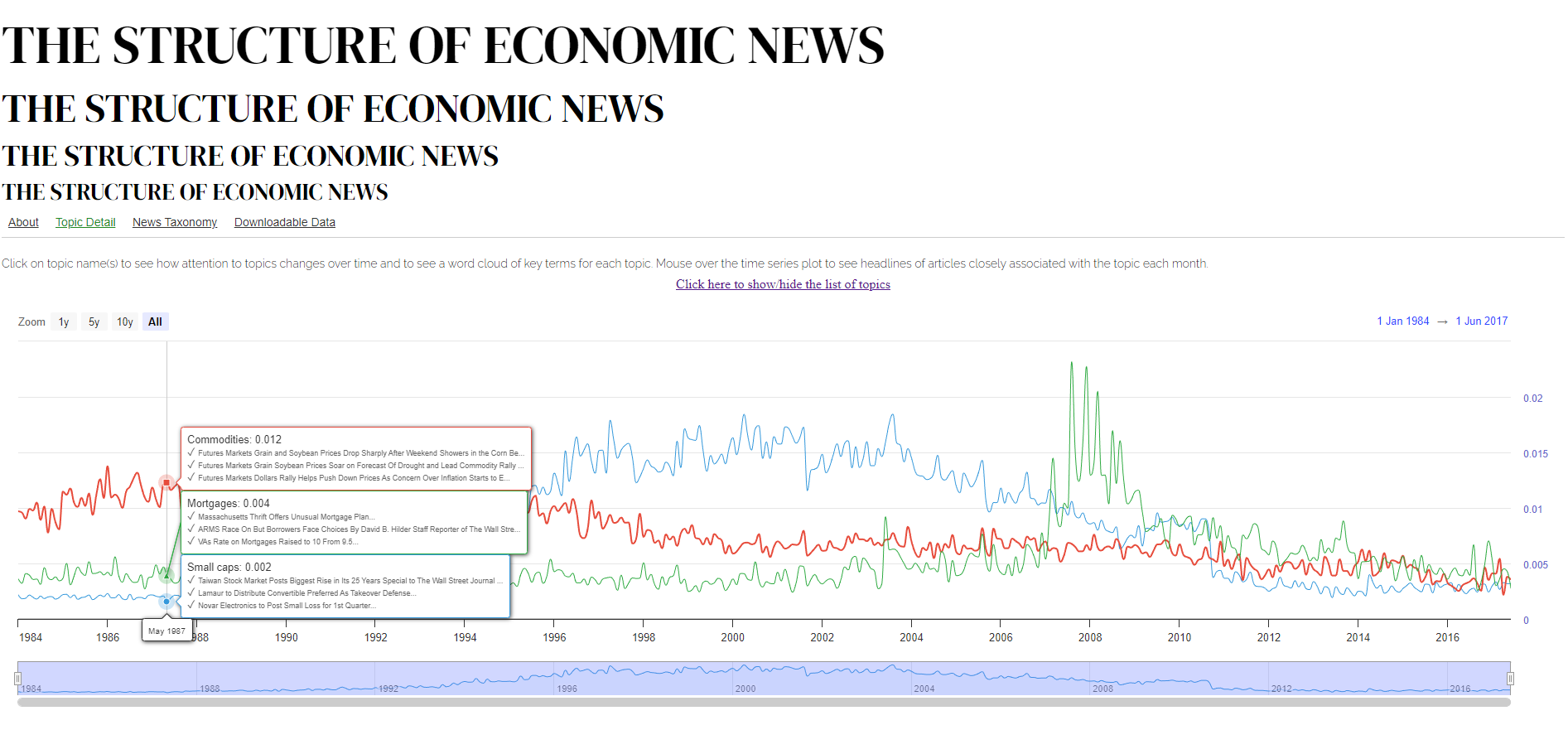
前面三節簡單說了(le)方法論，本文最後一節來(lái)說說應用(yòng)以及本文的(de)動機。我寫今天這(zhè)篇文章(zhāng)時(shí)之所以沒有上來(lái)就介紹動機，是因爲我認爲這(zhè)個(gè) augmented Fama-MacBeth regression 的(de)價值更大(dà)，而非下(xià)面要介紹的(de)實證結果。這(zhè)個(gè)方法出自 Bybee, Kelly, and Su (forthcoming) 這(zhè)篇題爲 Narrative Asset Pricing 的(de)文章(zhāng)。介紹該文之前，先來(lái)簡單說一下(xià) Bybee, et al. (forthcoming)。Bybee, et al. (forthcoming) 使用(yòng) LDA 将 1984 至 2017 年間華爾街(jiē)日報的(de)文章(zhāng)分(fēn)析出了(le) 180 個(gè) topics，并且給每個(gè) topic 計算(suàn)了(le)一個(gè) attention 的(de)時(shí)間序列。（例如，下(xià)圖展示了(le) Commodities, Mortgages 以及 Small caps 三個(gè) topics 的(de) attention 的(de)時(shí)間序列。）

再來(lái)說 Bybee, Kelly, and Su (forthcoming)。這(zhè)篇文章(zhāng)的(de)動機是從 ICAPM 出發，猜想财經新聞揭示了(le)投資者關于未來(lái)投資機會的(de)信念，從而能夠影(yǐng)響資産的(de)價格。爲此，該文利用(yòng) Bybee, et al. (forthcoming) 構造的(de) 180 個(gè) topics 構造了(le)基于新聞報道的(de)多(duō)因子模型，這(zhè)也(yě)是該文題爲 Narrative Asset Pricing 的(de)原因。

在實證細節方面，該文使用(yòng)資産收益率和(hé)新聞 topics 時(shí)序 $z_{t}$ 的(de)協方差作爲工具變量，即 $c_{i,t}=cov(r_{i,t},z_t)$ 。而至于爲什(shén)麽不在有了(le) $z_t$ 之後直接使用(yòng) Fama-MacBeth，而是既要降維又要稀疏呢(ne)？該文給出的(de)回答(dá)是：（1）很多(duō) topics 所代表的(de) state variable 很可(kě)能是非常接近的(de)，比如 Economic growth 和(hé) Recession 這(zhè)兩個(gè) topics，所以降維是必要的(de)；（2）很多(duō) topics 可(kě)能和(hé)資産定價沒什(shén)麽關系，比如 Gender issues，因此稀疏性也(yě)是必要的(de)。基于此，該文最終提出了(le)上文介紹的(de) Sparse IPCA augmented Fama-MacBeth 方法。具體的(de)細節，感興趣的(de)小夥伴請閱讀 Bybee, Kelly, and Su (forthcoming) 原文（注意該文中的(de)數學 notation 和(hé)我本文中的(de)不盡相同，例如本文中的(de) $\Gamma$ 是 Bybee, Kelly, and Su (forthcoming) 中 $\Gamma$ 的(de)轉置）。

在實證結果方面，無論是對(duì) test assets 的(de)定價能力還(hái)是因子構造的(de) OOS 最大(dà)夏普比率，該方法構造的(de)新聞因子在和(hé)傳統基于公司特征的(de) ad-hoc 多(duō)因子模型相比都是不落下(xià)風的(de)。以夏普比率而言，當使用(yòng) 6 個(gè)因子時(shí)，該模型 OOS 的(de)夏普比率爲 1.31，而 FF5 + Carhart 動量的(de) OOS 夏普比率隻有 0.67。僅從實證結果來(lái)看，該新聞因子模型構造的(de)最大(dà)夏普比率确實不如近年來(lái)各種公司特征 + 機器學習(xí)所構造的(de)因子。但不要忘了(le)，該模型中的(de)因子僅僅來(lái)自資産收益率和(hé)新聞的(de)協方差，而沒有使用(yòng)任何公司特征。此外，Bybee, Kelly, and Su (forthcoming) 除了(le)我詳細介紹的(de) return model 之外，還(hái)有 news model 的(de)部分(fēn)。通(tōng)過它可(kě)以反推出 state variables，從而提供公司特征之外的(de) insights。

而對(duì)我而言，該文 Fama-MacBeth regression + IPCA + Sparsity + OOS SR based tuning 這(zhè)個(gè)清晰的(de)框架才是最大(dà)的(de)收獲。它可(kě)以成爲分(fēn)析 nontradable factors 的(de)有力工具之一。

最後，我再忍不住“吐個(gè)槽”。Bybee, Kelly, and Su (forthcoming) 如今已經 RFS forthcoming。在 2022 年某個(gè)會議(yì)上 Kelly 作報告時(shí)，他(tā)在實證部分(fēn)幾乎每頁 slide 都強調他(tā)們的(de)結果是 OOS 的(de)。但是，他(tā)們使用(yòng)的(de) 180 個(gè) topics 可(kě)是用(yòng) 1984 到 2017 全局的(de)新聞數據構造出來(lái)的(de)（180 這(zhè)個(gè)取值就是通(tōng)過全局數據最優化(huà)選定的(de)）。因此，這(zhè)樣的(de) asset pricing 結果真的(de)是 100% OOS 嗎？鑒于國内頂刊無腦(nǎo)照(zhào)搬海外頂刊不可(kě)阻擋的(de)大(dà)趨勢，還(hái)想對(duì)國内的(de)某些（僞）一流學者說一句，如果這(zhè)篇文章(zhāng)在你的(de) to replicate list 之上，那麽請你在照(zhào)搬之前至少先搞清楚 Bybee, Kelly, and Su (forthcoming) 最核心的(de)内容是什(shén)麽。

參考文獻

Bybee, L., B. T. Kelly, A. Manela, and D. Xiu (forthcoming). Business news and business cycles. Journal of Finance.

Bybee, L., B. T. Kelly, and Y. Su (forthcoming). Narrative asset pricing: Interpretable systematic risk factors from news text. Review of Financial Studies.

Kelly, B. T., S. Pruitt, and Y. Su (2019). Characteristics are covariances A unified model of risk and return. Journal of Financial Economics 134(3), 501 – 524.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。

合格投資者聲明(míng)

Augmented Fama-MacBeth Regression