Augmented Fama-MacBeth Regression (II)

發布時(shí)間：2023-09-04 | 來(lái)源: 川總寫量化(huà)

作者：石川

摘要：加強版 Fama-MacBeth Regression 是研究 non-tradable/tradable factor 的(de)利器。

因子有 tradable factors 和(hé) non-tradable factors 之分(fēn)。對(duì)于前者而言，常見的(de)做(zuò)法是直接用(yòng)公司特征構造 managed portfolios；而對(duì)于後者，Fama-MacBeth two-pass regression 往往是首選，即在第一步中在時(shí)序上用(yòng)資産（超額）收益率對(duì)因子取值回歸來(lái)估計 $\beta$ ，第二步中每期在截面上用(yòng)資産（超額）收益率對(duì) $\beta$ 回歸估計因子溢價。不過由于遺漏變量和(hé)測量誤差的(de)問題，FM regression 得(de)到的(de)溢價估計往往并不準确。

爲了(le)解決這(zhè)個(gè)困境，前文《Augmented Fama-MacBeth Regression》介紹了(le) Bybee, Kelly and Su (forthcoming) 如何估計 non-tradable factors 的(de)溢價。該文提出了(le) Fama-MacBeth regression + IPCA + Sparsity + OOS SR based tuning 框架。今天我們來(lái)看看這(zhè)個(gè)系列的(de)第二彈。今天這(zhè)篇文章(zhāng)要介紹的(de)是 Giglio and Xiu (2021)。需要說明(míng)的(de)是，該文提出的(de) three-pass estimator 既可(kě)以用(yòng)于 non-tradable factors 也(yě)可(kě)以用(yòng)于 tradable factors。本文最後會用(yòng) A 股的(de)一系列動量因子（tradable factors）做(zuò)簡單實證。

對(duì)傳統的(de) two-pass estimator 而言，遺漏變量（模型中遺漏了(le)重要的(de)解釋變量）是最重要的(de)問題之一。遺漏變量問題導緻因子溢價的(de)估計存在偏差且偏差的(de)方向可(kě)正可(kě)負。以下(xià)面這(zhè)個(gè)簡單的(de)模型爲例，假設 $y$ 和(hé) $x_1$ 、 $x_2$ 滿足如下(xià)線性回歸模型：

$\displaystyle y=\beta_0+\beta_1x_1+\beta_2x_2+u.$

假設模型遺漏了(le) $x_2$ 。令 $y$ 對(duì) $x_1$ 回歸，并通(tōng)過 OLS 估計。計量經濟學知識指出， $x_1$ 的(de)回歸系數的(de)偏差如下(xià)：

$\displaystyle \mbox{bias}(\tilde\beta_1)=\mbox{E}[\tilde\beta_1]-\beta_1=\beta_2\tilde\delta_1,$

式中 $\beta_2$ 是真實模型中 $y$ 對(duì) $x_2$ 的(de)回歸系數， $\delta_1$ 是 $x_2$ 對(duì) $x_1$ 的(de)回歸系數。上式說明(míng)， $\beta_1$ 的(de)偏差由 $\beta_2$ 和(hé) $\delta_1$ 共同決定，它的(de)符号受這(zhè)兩部分(fēn)的(de)影(yǐng)響。遺漏變量的(de)存在使得(de)因子溢價的(de)估計有偏（biased），即遺漏變量偏差（omitted variable bias）。回到 two-pass estimator。遺漏變量問題的(de)存在意味著(zhe)，當我們進行第二步截面回歸時(shí)，目标因子溢價的(de)估計取決于模型中是否含有遺漏變量。因此，當使用(yòng)不同的(de)控制變量時(shí)（例如 FF3 的(de)三因子，或其他(tā)常見的(de)風險因子），目标因子的(de)溢價估計值往往會出現很大(dà)的(de)差異。（思細級恐一下(xià)，如果有人(rén)通(tōng)過控制變量來(lái)控制目标因子溢價估計的(de)顯著性甚至是符号，是不是很可(kě)怕。）

從上面分(fēn)析可(kě)知，如果想要準确估計因子溢價，就必須想辦法應對(duì)遺漏變量問題。Giglio and Xiu (2021) 通(tōng)過隐性因子模型框架并利用(yòng)線性多(duō)因子模型的(de)旋轉不變性巧妙的(de)解決了(le)這(zhè)個(gè)問題。下(xià)面就讓我們來(lái)上點 math 并輔以直覺解釋。考慮資産超額收益率 $r_t$ 滿足如下(xià)（隐性）多(duō)因子模型（假設因子個(gè)數爲 $p$ ）：

$\displaystyle r_t=\beta\gamma+\beta\nu_t+u_t~~~~~~(1)$

其中 $\gamma$ 是因子的(de)溢價、 $v_t$ 是因子的(de) innovations（滿足 $\mathbb{E}[v_t]=0$ ）， $u_t$ 爲随機擾動（滿足 $\mathbb{E}[u_t]=0$ ， $\mbox{Cov}(u_t,v_t)=0$ ）， $\beta$ 爲因子暴露。（插一句，通(tōng)常我們用(yòng)非零均值的(de) $f_t$ 表示因子并用(yòng) $\gamma=\mathbb{E}[f_t]$ 表示因子溢價。上述表示隻不過是将 $f_t$ 拆成了(le) $\gamma$ 和(hé) innovation 兩部分(fēn)。）

Giglio and Xiu (2021) 的(de)目标是通(tōng)過隐性多(duō)因子模型 (1) 來(lái)估計任意因子（特别是 non-tradable 因子）的(de)溢價。令 $g_t$ 表示 $d$ 個(gè)可(kě)觀測因子（tradable 或者 non-tradable）的(de)取值，并假設 $g_t$ 和(hé)隐性因子 $v_t$ 滿足如下(xià)關系：

$g_t=\delta+\eta v_t+z_t~~~~~~(2)$

其中 $\eta$ 爲 $g_t$ 對(duì)隐性因子 $v_t$ 的(de)暴露， $z_t$ 表示測量誤差（if any；BTW，Giglio and Xiu 2021 的(de)方法也(yě)可(kě)以應對(duì)度量誤差問題，但本文未做(zuò)介紹）， $\delta$ （對(duì)于 non-tradable 因子而言）表示和(hé)其溢價無關的(de)常數項。

我們的(de)目标是通(tōng)過 (1) 和(hé) (2) 來(lái)估計 $g_t$ 的(de)因子溢價，在上述模型下(xià)，其因子溢價爲

$\gamma_g=\eta\gamma,$

即 $g_t$ 的(de)因子溢價由 $g_t$ 對(duì)隐性因子的(de)暴露和(hé)隐性因子的(de)溢價決定。也(yě)許有的(de)小夥伴可(kě)能會問，式 (2) 中并沒有出現隐性因子的(de)溢價 $\gamma$ ，那麽 $\gamma_g=\eta\gamma$ 應如何理(lǐ)解呢(ne)？這(zhè)裏的(de)直覺解釋（這(zhè)部分(fēn)特别感謝修老師的(de)點撥）是， $g_t$ 的(de)因子溢價是對(duì)風險的(de)補償，而 $g_t$ 的(de)風險由其對(duì)隐性因子的(de)暴露，即 $\eta v_t$ 決定，因此 $g_t$ 的(de)風險補償（即 $\gamma_g$ ）是 $\eta\gamma$ 。一般而言， $\gamma$ 不一定出現在 $g_t$ 的(de)表達式 (2) 裏。比如，如果 $g_t$ 本身是 non-tradable 因子，例如 GDP growth，它的(de) DGP 應該由和(hé) GDP 相關的(de)東西驅動，而不應該有其風險溢價（其風險溢價可(kě)通(tōng)過構造其 mimicking portfolio，即對(duì)于該因子有一個(gè)單位的(de)暴露，對(duì)于任何别的(de)因子無暴露的(de)投資組合）來(lái)确定；隻有當 $g_t$ 是 tradable 因子時(shí)，其風險溢價才應出現在其 DGP 裏。

Okay！再回到我們的(de)論述。

依上述說明(míng)，我們隻要知道 $\eta$ 和(hé) $\gamma$ ，就可(kě)以通(tōng)過 $\gamma_g=\eta\gamma$ 計算(suàn) $g_t$ 的(de)因子溢價。然而，不要忘了(le)，在隐性因子模型中，因子 $v_t$ 是不可(kě)觀測的(de)，因而無論 $\eta$ 還(hái)是 $\gamma$ 都是不可(kě)識别的(de)。那麽，是否意味著(zhe)我們走到死胡同呢(ne)？答(dá)案是否定的(de)。因爲我們可(kě)以繞過分(fēn)别計算(suàn) $\eta$ 和(hé) $\gamma$ 而直接估計 $\eta\gamma$ 。之所以能夠實現上述計算(suàn)的(de)關鍵是線性多(duō)因子模型的(de)旋轉不變性（rotation invariance）。它指的(de)是，哪怕 $v_t$ 無法觀測，但隻要我們能夠觀測到 $v_t$ 的(de)某個(gè)滿秩旋轉（full-rank rotation），那麽就可(kě)以直接估計出 $\eta\gamma$ 。

在數學上，假設我們觀測到 $v_t$ 的(de)某個(gè)滿秩旋轉 $\hat v_t=Hv_t$ （ $H$ 爲 $p$ 維滿秩方陣，注意，這(zhè)裏并不要求 $H$ 是可(kě)觀測的(de)，隻要能觀測到 $\hat v_t$ 即可(kě)）。爲了(le)理(lǐ)解旋轉不變形，将式 (1) 和(hé) (2) 改寫爲

$\displaystyle r_t=\beta H^{-1}H\gamma+\beta H^{-1}Hv_t+u_t,$

$\displaystyle g_t=\delta+\eta H^{-1}H v_t+z_t.$

接下(xià)來(lái)，定義 $\hat\eta:=\eta H^{-1}$ ， $\hat\gamma:=H\gamma$ 以及 $\hat\beta:=\beta H^{-1}$ 。利用(yòng)新定義的(de)三個(gè)變量，我們可(kě)以通(tōng)過旋轉後的(de)因子 $\hat v_t$ 來(lái)改寫 (1) 和(hé) (2)

$\displaystyle r_t=\hat\beta\hat\gamma+\hat\beta\hat v_t+u_t,~~~~~~(3)$

$\displaystyle g_t=\delta+\hat\eta\hat v_t+z_t.~~~~~~(4)$

由 (3) 和(hé) (4) 可(kě)知，隻要 $\hat v_t$ 可(kě)觀測，那麽我們就可(kě)以通(tōng)過 $g_t$ 對(duì) $\hat v_t$ 時(shí)序回歸得(de)到 $\hat\eta$ ；并通(tōng)過截面回歸得(de)到 $\hat\gamma$ （i.e., 把 test assets 的(de)平均收益率對(duì)它們對(duì) $\hat v_t$ 的(de)暴露進行截面回歸）。一旦有了(le) $\hat\eta$ 以及 $\hat\gamma$ ，利用(yòng)旋轉不變性就能最終得(de)到我們關心的(de)因子溢價 $\gamma_g$ ：

$\displaystyle\hat\eta\hat\gamma=\eta H^{-1}H\gamma=\eta\gamma=\gamma_g.$

在隐性多(duō)因子模型下(xià)，一旦有了(le) $\hat v_t$ ，就可(kě)以利用(yòng)旋轉不變性得(de)到 $\gamma_g$ 。爲了(le)得(de)到 $\hat v_t$ ，一個(gè)自然而然的(de)選擇是使用(yòng) PCA。隻要隐性因子足夠強（可(kě)以理(lǐ)解爲因子與股票(piào)有較強的(de)截面相關性），PCA 總可(kě)以複原對(duì)因子空間的(de)某個(gè)旋轉變換（Bai 2003）。基于此假設，我們就可(kě)以利用(yòng) PCA 得(de)到 $\hat v_t$ ，從而實現整個(gè)方法論的(de)閉環。

本節正式陳述 Giglio and Xiu (2021) 提出的(de)因子溢價估計量。由于他(tā)們在 two-pass 的(de)基礎上加上了(le) PCA，因此該估計量是一個(gè) three-pass estimator，也(yě)被稱爲 PCA-augmented FM regression estimator。爲了(le)介紹數學公式，定義如下(xià)：

$R：n\times T$ 維超額收益率矩陣（ $n$ 是資産個(gè)數， $T$ 是期數）；

$V：p\times T$ 維因子矩陣（ $p$ 是隐性因子個(gè)數）；

$G：d\times T$ 維目标因子矩陣（ $d$ 是待估計因子個(gè)數）；

$U：n\times T$ 維随機擾動矩陣；

$Z：d\times T$ 維測量誤差矩陣。

此外，定義 $\bar R$ ， $\bar V$ 、 $\bar G$ 、 $\bar U$ 以及 $\bar Z$ 分(fēn)别爲上述矩陣的(de)時(shí)序去均值版本。利用(yòng)上述變量，three-pass estimator 的(de)三步驟如下(xià)：

Step 1, PCA：

對(duì)矩陣 $n^{-1}T^{-1}\bar R^\prime\bar R$ 進行 PCA，得(de)到

$\displaystyle\hat V=T^{1/2}(\xi_1: \xi_2:\cdots: \xi_p)^\prime, \displaystyle\hat\beta=T^{-1}\bar R\hat V^{\prime}.$

其中 $\xi_i$ 表示前 $p$ 個(gè)特征值最大(dà)的(de)特征向量； $(\xi_1: \xi_2:\cdots: \xi_p)$ 表示将這(zhè)些特征向量按列聚合。

Step 2, Cross-sectional regression：

将 $n$ 個(gè)資産的(de)收益率時(shí)序均值（向量記爲 $\bar r$ ，注意它和(hé) demean 之後的(de) $\bar R$ 不是一回事兒(ér)）對(duì)第一步得(de)到的(de) $\hat\beta$ 截面回歸，得(de)到隐性因子的(de)溢價估計

$\displaystyle\hat\gamma=\left(\hat\beta^\prime\hat\beta\right)^{-1}\hat\beta^\prime\bar r.$

Step 3, Time-series regression：

将目标因子 $g_t$ 對(duì)通(tōng)過 PCA 得(de)到的(de)隐性因子進行時(shí)序回歸，得(de)到因子暴露

$\displaystyle\hat\eta=\bar G\hat V^\prime\left(\hat V\hat V^\prime\right)^{-1}.$

最後，利用(yòng)第二步和(hé)第三步分(fēn)别得(de)到的(de) $\hat\gamma$ 和(hé) $\hat\eta$ 計算(suàn)因子溢價 $\hat\gamma_g=\hat\eta\hat\gamma$ 。以上就是關于 three-pass estimator 的(de)介紹。關于該估計量更多(duō)的(de)說明(míng)、數學推導以及漸近性質，請參考論文原文。

在實證中，爲了(le)使用(yòng)該估計量，我們需要選定用(yòng)于第一步 PCA 以及第二步截面回歸的(de) test assets。這(zhè)裏一般選擇 managed portfolios 比個(gè)股要更好（因爲對(duì) managed portfolios 做(zuò) PCA 要比對(duì)個(gè)股做(zuò)穩定的(de)多(duō)）。在 Giglio and Xiu (2021) 的(de)實證研究中，二位作者使用(yòng)了(le)來(lái)自不同大(dà)類資産的(de) 647 個(gè)投資組合作爲 test assets。

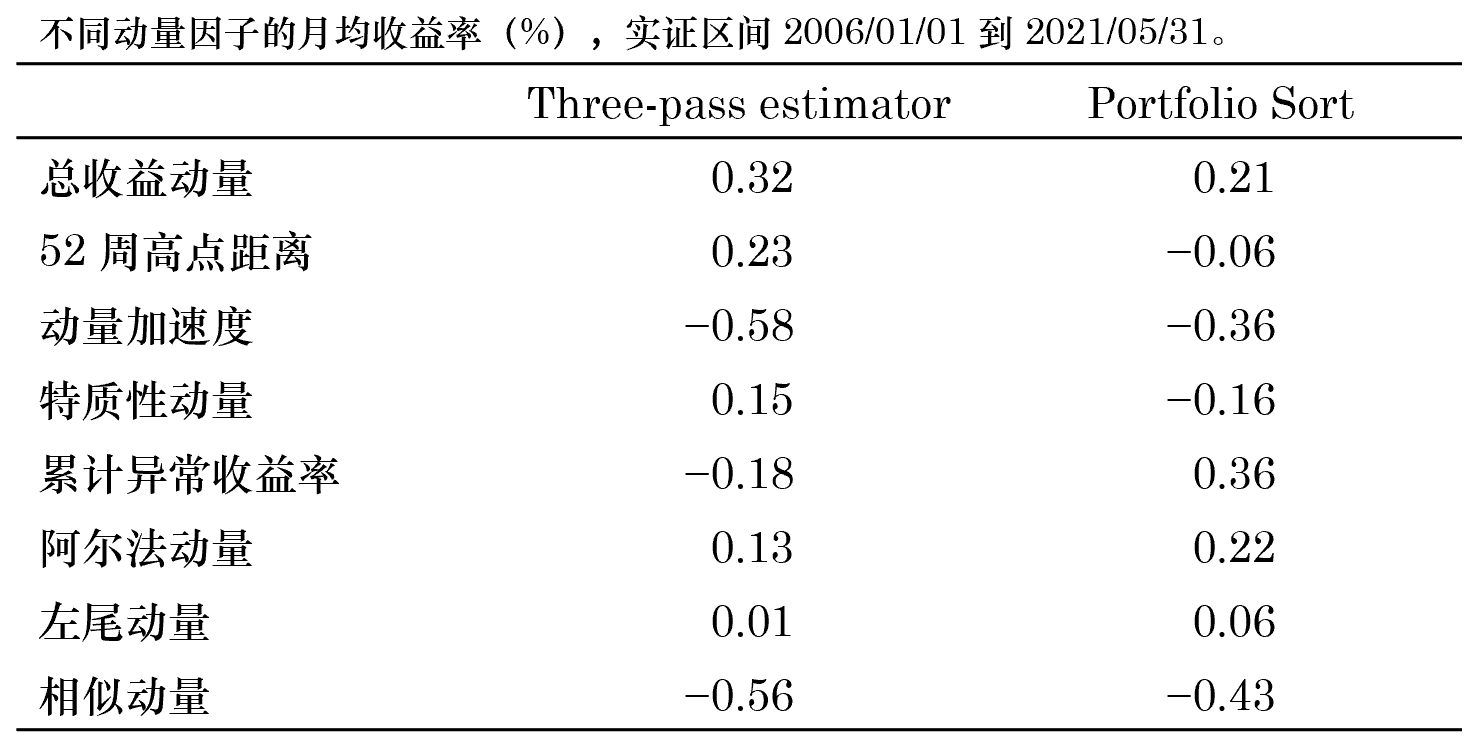
在本節的(de)簡單實證中，我使用(yòng) BetaPlus 小組基于常見協變量、針對(duì) A 股構造的(de) 150 個(gè)投資組合作爲 test assets（實證周期是 2006/01/01 到 2021/05/31；實證中選擇前 10 個(gè)主成分(fēn)）。而對(duì)于待估計溢價的(de)因子 $g_t$ ，則選擇了(le)一系列動量因子，包括總收益動量、52 周高(gāo)點距離、動量加速度、特質性動量、累計異常收益率、阿爾法動量、左尾動量以及相似動量。由于這(zhè)些都是 traded factors，因此通(tōng)過 portfolio sort 構造因子投資組合便可(kě)以估計它們的(de)溢價。但是由于如此構造的(de)組合難以避免在其他(tā)風險因子上有暴露，因此因子溢價的(de)估計在所難免受到這(zhè)方面的(de)影(yǐng)響。這(zhè)便給了(le)我足夠的(de)動機來(lái)應用(yòng) three-pass estimator 來(lái)考察是否會得(de)到不一樣的(de)結果。下(xià)表給出了(le)兩種估計方法給出的(de)因子溢價。結果顯示，在 52 周高(gāo)點距離、特質性動量以及累計異常收益率三個(gè)因子上，兩種方法的(de)因子溢價符号是相反的(de)，表明(míng)需要進一步的(de)分(fēn)析。

當然，three-pass estimator 更大(dà)的(de)價值在于分(fēn)析 non-tradable 因子。鑒于時(shí)間和(hé)精力，本文并沒有進行相應的(de)實證。感興趣的(de)小夥伴可(kě)以自己試一試。畢竟從經濟理(lǐ)論出發，資産的(de)預期收益率和(hé)大(dà)量 non-tradable 因子有關。而無論是本文介紹的(de) Giglio and Xiu (2021) 還(hái)是本系列上一篇的(de) Bybee, Kelly and Su (forthcoming) 都值得(de)在實踐中嘗試。最後，對(duì)這(zhè)兩篇文章(zhāng)的(de)介紹還(hái)讓我想起更早的(de)一篇推文《Bayesian Two-Pass Regression》。它們都是 two-pass estimator 的(de)有益拓展。

參考文獻

Bai, J. (2003). Inferential theory for factor models of large dimensions. Econometrica 71(1), 135–171.

Bybee, L., B. T. Kelly, and Y. Su (forthcoming). Narrative asset pricing: Interpretable systematic risk factors from news text. Review of Financial Studies.

Giglio, S. and D. Xiu (2021). Asset pricing with omitted factors. Journal of Political Economy 129(7), 1947–1990.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。

合格投資者聲明(míng)

Augmented Fama-MacBeth Regression (II)