Risk-Return Tradeoffs (I)

發布時(shí)間：2023-09-27 | 來(lái)源: 川總寫量化(huà)

作者：石川

摘要：隐性多(duō)因子模型如何成爲研究資産定價的(de)重要範式？且聽(tīng) Kelly and Xiu (2023) 娓娓道來(lái)。

上期文章(zhāng)介紹了(le) Giglio and Xiu (2021) 提出的(de) three-pass estimator。它在 Fama-MacBeth regression 的(de)基礎上加入了(le) PCA，是近年來(lái)通(tōng)過 PCA 研究隐性因子模型的(de)代表之一。

在隐性因子模型中，因子暴露和(hé)因子都是不可(kě)觀測的(de)，而是需要通(tōng)過統計手段估計得(de)到（因此按照(zhào) FF 方法構造的(de) HML 就不是隐性因子）。在這(zhè)方面，對(duì)（大(dà)量）資産的(de)協方差矩陣進行 PCA 就是最重要的(de)工具之一，而這(zhè)背後的(de)理(lǐ)論基礎正是源自 APT。這(zhè)樣得(de)到的(de)因子也(yě)被稱爲統計因子（statistical factors）。

當然，如果僅僅是從資産的(de)協方差矩陣出發，那麽能夠利用(yòng)的(de)信息将會十分(fēn)有限（即隻用(yòng)了(le)收益率信息）。爲了(le)利用(yòng)到更多(duō)的(de)信息（例如 firm characteristics），可(kě)以将因子暴露直接建模爲特征的(de)函數，即 $\beta(X)$ 。這(zhè)就是 Bryan Kelly 等人(rén)提出的(de) Instrument-PCA（IPCA）模型。在數學上，它近似等價于對(duì)使用(yòng)這(zhè)些特征構造的(de)一大(dà)堆 managed portfolios 的(de)收益率的(de)協方差矩陣進行 PCA，因此和(hé)直接對(duì)資産協方差矩陣進行 PCA 有異曲同工之妙。不過工具變量（那些 characteristics）的(de)引入使該模型成爲條件因子模型，因此能夠更好地刻畫(huà)資産收益率的(de)時(shí)變性。

鋪墊了(le)這(zhè)麽多(duō)，是因爲今天我想翻譯一下(xià) Kelly and Xiu (2023) 的(de)第四章(zhāng)（Risk-Return Tradeoffs）—— 對(duì)，我把第三章(zhāng)跳過去了(le)。第四章(zhāng)中涉及的(de)最重要兩篇文章(zhāng)就是 Giglio and Xiu (2021) 以及 Kelly et al. (2019) 的(de) IPCA 模型。此外，由于原著的(de)第四章(zhāng)内容過于豐富，本文隻覆蓋到其中的(de) 4.3 節。後面的(de)三小節将會在後續推文中介紹。

再次感謝王熙和(hé)劉洋溢對(duì)内容的(de)反饋。本翻譯僅供學習(xí)交流使用(yòng)，禁止一切商業行爲，未經授權，禁止轉載。

最後，祝各位中秋、國慶節快(kuài)樂(yuè)。

以下(xià)是正文部分(fēn)。

上一章(zhāng)主要關注于監督預測模型而沒有考慮風險和(hé)收益率之間的(de)權衡，因此它們并不是資産定價模型。本章(zhāng)将通(tōng)過無監督和(hé)半監督學習(xí)方法提出因子定價模型，它們明(míng)确地考慮了(le)風險和(hé)收益率之間的(de)權衡問題。

4.1 套利定價理(lǐ)論基礎

Ross (1976) 的(de)套利定價理(lǐ)論（APT）爲數據驅動的(de)和(hé)基于機器學習(xí)的(de)因子模型分(fēn)析奠定了(le)基礎。它表明(míng)，通(tōng)過部分(fēn)模型設定 —— 本質上隻需假設線性因子結構，因子數量固定，以及無套利這(zhè)一基礎的(de)經濟假設 —— 我們便能方便地通(tōng)過研究因子組合來(lái)學習(xí)資産定價模型，并了(le)解收益率中哪部分(fēn)是可(kě)以分(fēn)散化(huà)的(de)，而哪部分(fēn)則不能。換句話(huà)說，APT 爲關于風險與收益率權衡的(de)實證分(fēn)析提供了(le)一個(gè)藍圖，而無需使用(yòng)者了(le)解導緻資産定價因子背後的(de)機制。因此，我們可(kě)以利用(yòng)機器學習(xí)方法進行隐性因子分(fēn)析，從而得(de)出關于實證資産定價現象的(de)全新見解。

我們還(hái)推薦讀者參閱 Giglio et al. (2022a) 關于收益率因子模型的(de)綜述。在這(zhè)篇綜述中，幾位作者依照(zhào)因子是否是可(kě)觀測的(de)、 $\beta$ 值是否是可(kě)觀測的(de)或兩者都是不可(kě)被觀測這(zhè)幾條标準将文獻分(fēn)類。針對(duì)可(kě)觀測的(de)因子或 $\beta$ ，學者們已經提出了(le)很多(duō)時(shí)序和(hé)截面回歸方法。在本章(zhāng)中，我們聚焦于一個(gè)更具挑戰性的(de)情況，即因子和(hé) $\beta$ 都是隐性的(de)（或最多(duō)隻是部分(fēn)可(kě)觀測的(de)），以便能夠深入探討(tǎo)一些機器學習(xí)因子建模的(de)技術細節。

4.2 無條件因子模型

Ross (1976) 的(de) APT 是以如下(xià)這(zhè)個(gè)統計因子模型爲前提：

$R_t=\alpha+\beta F_t+\epsilon_t, ~~~~~~(4.1)$

其中 $N\times 1$ 維向量 $R_t$ 表示單個(gè)資産的(de)超額收益 $R_{i,t}$ ， $N\times K$ 維矩陣 $\beta$ 表示這(zhè)些資産對(duì) $K$ 個(gè)隐性因子 $F_t$ 的(de)暴露， $F_t$ 的(de)非零均值 $\gamma=\mathbb{E}[F_t]$ 則可(kě)以被理(lǐ)解爲因子的(de)風險溢價（譯者注：即因子收益率，這(zhè)一結論成立的(de)充分(fēn)條件是因子可(kě)以被交易），最後 $N\times 1$ 維向量 $\epsilon_t$ 則表示均值爲零的(de)随機擾動。

另外， $N\times 1$ 維截距向量 $\alpha$ 表示定價誤差。它們是資産預期收益率中無法被對(duì)風險因子的(de)暴露所解釋的(de)部分(fēn)。Ross (1976) 的(de) APT 以及其後繼者們（例如 Huberman 1982, Ingersoll 1984, Chamberlain and Rothschild 1983）指出，無近似套利條件等價于

$\displaystyle \alpha^\prime\mbox{Var}(\epsilon_t)^{-1}\alpha\lesssim_P 1,~~\mbox{as}~~N\rightarrow\infty.~~~~~~(4.2)$

上式意味著(zhe)，承擔特質性風險的(de)補償并不會随著(zhe)投資範圍的(de)擴大(dà)而激增（譯者注：根據原著腳注的(de)說明(míng)， $a \lesssim_P b$ 代表 $a=O_P(b)$ ，其意思爲随著(zhe)樣本量趨于無窮大(dà)， $a$ 的(de)增長(cháng)率不會超過 $b$ 的(de)某個(gè)固定的(de)倍數。此外，在後文中，原著使用(yòng) $a\asymp_P b$ 表示 $a \lesssim_P b$ 以及 $b \lesssim_P a$ 兩個(gè)條件同時(shí)滿足）。

4.2.1 使用(yòng) PCA 估計因子

受 APT 的(de)啓發，Chamberlain and Rothschild (1983)，Connor and Korajczyk (1986) 以及 Connor and Korajczyk (1988) 均主張，當因子和(hé)因子暴露均無法觀測時(shí)，使用(yòng)主成分(fēn)分(fēn)析（PCA）作爲因子模型的(de)估計方法。爲此，一個(gè)等價但更方便的(de)處理(lǐ)方法是對(duì)去均值之後的(de)收益率 $\bar{R}=R-(\frac{1}{T}\sum_{t=1}^TR_t)\iota^\prime_T$ 進行奇異值分(fēn)解（SVD）：

$\displaystyle\bar{R}=\sum_{j=1}^{\widehat{K}}\sigma_j\varsigma_j\xi_j^\prime+\widehat{U},~~~~~~(4.3)$

其中 $\{\sigma_j\}$ 、 $\{\varsigma_j\}$ 以及 $\{\xi_j\}$ 分(fēn)别表示 $\bar{R}$ 的(de)前 $\widehat{K}$ 個(gè)奇異值，以及左、右奇異向量， $\widehat{K}$ 爲 $R_t$ 中因子個(gè)數的(de)任意一緻估計量（例如 Bai and Ng 2002）， $\widehat{U}$ 爲殘差矩陣， $\iota_T$ 表示其元素均爲 $1$ 的(de) $T\times 1$ 維向量。通(tōng)過上述奇異值分(fēn)解可(kě)以得(de)到因子變化(huà) $V_t=F_t-\mathbb{E}[F_t]$ 和(hé)風險暴露 $\beta$ 的(de)估計值

$\begin{array}{l} \displaystyle\widehat{V}=T^{1/2}(\xi_1,\xi_2,\cdots,\xi_{\widehat{K}})^\prime,\\ \displaystyle\widehat{\beta}=T^{-1/2}(\sigma_1\varsigma_1,\sigma_2\varsigma_2,\cdots,\sigma_{\widehat{K}}\varsigma_{\widehat{K}}).~~~~~~(4.4) \end{array}$

上述因子估計值是标準化(huà)的(de)，因而滿足 $\widehat{V}\widehat{V}^\prime=T\mathbb{I}_{\widehat{K}}$ 。類似的(de)，我們也(yě)可(kě)以将 $\widehat{\beta}$ 标準化(huà)，使其滿足 $\widehat{\beta}^\prime\widehat{\beta}=N\mathbb{I}_{\widehat{K}}$ 。在隐性因子模型中，存在一個(gè)基本的(de)不确定性，即旋轉因子并同時(shí)反向旋轉因子暴露不改變數據生成過程。因此，因子及其暴露的(de)可(kě)識别性僅限于一個(gè)可(kě)逆的(de)線性變換（即旋轉）。鑒于此，不同的(de)标準化(huà)會産生等價的(de)因子和(hé)因子暴露估計量，它們之間可(kě)以通(tōng)過某種旋轉而相互轉換。在所有因子都是普遍性的(de)假設下(xià)，即 $\lambda_K(\beta^\prime\beta)\asymp_P N$ ，Bai (2003) 證明(míng)了(le) PCA 估計的(de)一緻性并推導出它們在該假設下(xià)的(de)漸近分(fēn)布。

Connor and Korajczyk (1988) 最早使用(yòng)大(dà)約 1500 支股票(piào)研究了(le)隐性因子模型的(de)表現。他(tā)們發現，盡管基于 PCA 的(de)因子模型比起 CAPM 模型更能解釋樣本中的(de)風險和(hé)收益率，但它依然會産生很大(dà)且顯著的(de)定價誤差。一般來(lái)說，無條件因子模型很難描述個(gè)股級别的(de)數據。基于該研究以及其他(tā)相關研究，無條件隐性因子模型（及其通(tōng)過 PCA 的(de)估計）自 Connor and Korajczyk (1988) 之後便淡出了(le)人(rén)們的(de)視線。Kelly et al. (2019) 利用(yòng)最新的(de)數據也(yě)證實了(le)上述發現。他(tā)們顯示，在橫跨 1962—2014 年的(de) CRSP 股票(piào)面闆數據中，PCA 在估計個(gè)股風險溢價方面極不穩健。

近年來(lái)，利用(yòng) PCA 對(duì)收益率因子建模再次回到了(le)人(rén)們的(de)視線之中。這(zhè)個(gè)現象在很大(dà)程度上源于這(zhè)樣一個(gè)事實：盡管 PCA 在描述個(gè)股股票(piào)面闆數據時(shí)效果不理(lǐ)想，但它在對(duì)投資組合的(de)面闆數據建模方面取得(de)了(le)巨大(dà)的(de)成功。例如，Kelly et al. (2019), Kozak et al. (2018) 以及 Pukthuanthong et al. (2019) 均表明(míng)，通(tōng)過 PCA 分(fēn)析異象投資組合的(de)面闆數據而得(de)到的(de)因子模型能夠對(duì)這(zhè)些很好地爲這(zhè)些組合定價，表現爲經濟意義很小的(de)定價誤差。這(zhè)些分(fēn)析是建立在 Geweke and Zhou (1996) 的(de)早期工作之上，他(tā)們使用(yòng) Gibbs 抽樣法從投資組合級别數據中提取隐性因子。

對(duì)于隐性因子模型而言，由于該模型的(de)不确定性（譯者注：即可(kě)以通(tōng)過旋轉得(de)到等價的(de)模型），它的(de)一個(gè)潛在的(de)缺點是人(rén)們難以解釋估計出的(de)因子。然而，當我們關注的(de)對(duì)象不受旋轉影(yǐng)響時(shí)，使用(yòng)隐性因子模型就會變得(de)非常方便。下(xià)面我們就來(lái)看這(zhè)樣一個(gè)例子。

4.2.2 風險溢價的(de)三步法估計量

因子的(de)風險溢價等于均衡狀态下(xià)投資者因暴露于該因子的(de)風險而要求的(de)補償。許多(duō)理(lǐ)論經濟模型是基于一些不可(kě)交易因子（即因子本身并非某個(gè)投資組合），如消費、GDP 增長(cháng)、通(tōng)貨膨脹、流動性和(hé)氣候風險等，來(lái)開發的(de)。爲了(le)估計一個(gè)不可(kě)交易因子的(de)風險溢價，我們需要構建一個(gè)模拟該因子的(de)投資組合并估計其預期收益率。爲了(le)便于闡述，假設某個(gè)不可(kě)交易因子 $G_t$ 與資産的(de)截面關系如下(xià)：

$\displaystyle G_t=\xi+\eta V_t+Z_t,~~~~~~(4.5)$

其中 $Z_t$ 是測量誤差且 $V_t=F_t-\mathbb{E}[F_t]$ 。在這(zhè)個(gè)模型中， $G_t$ 的(de)風險溢價爲 $\eta\gamma$ 。由于 $G_t$ 往往是源自某些經濟理(lǐ)論，因此它的(de)模拟組合和(hé)風險溢價可(kě)能在經濟上是可(kě)解釋的(de)。此外，盡管 $V_t$ 、 $\eta$ 以及 $\gamma$ 的(de)可(kě)識别性僅限于可(kě)逆的(de)線性變換（旋轉），但 $\eta V_t$ 以及 $\eta\gamma$ 卻不受旋轉的(de)影(yǐng)響，因而是可(kě)以被識别的(de)。爲了(le)理(lǐ)解這(zhè)一點，由 Bai and Ng (2002) 可(kě)知存在矩陣 $H$ 使得(de) $\widehat{V}_t\xrightarrow{P} HV_t$ （對(duì)任意 $t$ ）。如果我們利用(yòng) $HV_t$ 表示 $R_t$ 和(hé) $G_t$ 的(de)數據生成過程，那麽 $V_t$ 的(de)風險溢價可(kě)以表示爲 $H\gamma$ ，且 $G_t$ 對(duì) $HV_t$ 的(de)暴露變爲 $\eta H^{-1}$ ，然而模拟組合的(de)因子突變以及 $G_t$ 的(de)風險溢價卻不受上述旋轉的(de)影(yǐng)響，即 $\eta H^{-1}HV_t=\eta V_t$ 以及 $\eta H^{-1}H\gamma=\eta\gamma$ 。

通(tōng)過将 Fama-MacBeth 回歸與 PCA 相結合，Giglio and Xiu (2021) 提出一個(gè)三步法估計量來(lái)對(duì) $\eta\gamma$ 進行推斷。該估計量的(de)第一步是使用(yòng) PCA 并根據式 (4.4) 估計因子和(hé)暴露。第二步通(tōng)過 Fama-MacBeth 回歸求解隐性因子的(de)風險溢價：

$\displaystyle \widehat{\gamma}=\frac{1}{T}\sum_{t=1}^T\left(\widehat{\beta}^\prime\widehat{\beta}\right)^{-1}\widehat{\beta}^\prime R_t.~~~~~~(4.6)$

第三步則是計算(suàn) $G_t$ 對(duì)隐性因子的(de)暴露：

$\displaystyle\widehat{\eta}=\frac{1}{T}\sum_{t=1}^T G_t\widehat{V}_t^\prime.$

最終， $G_t$ 的(de)風險溢價估計量爲 $\widehat{\eta}\widehat{\gamma}$ 。

Giglio and Xiu (2021) 進一步給出了(le)該估計量的(de)漸近性質。他(tā)們對(duì)基于 PCA 結果的(de) Fama-MacBeth 回歸的(de)漸近分(fēn)析爲風險溢價、随機貼現因子（Giglio et al. 2021b）以及 $\alpha$ （Giglio et al. 2021a）等變量進行統計推斷鋪平了(le)道路，這(zhè)些變量均是人(rén)們使用(yòng)隐性因子模型進行資産定價時(shí)的(de)重要研究對(duì)象。

三步法估計量和(hé)基于 PCA 回歸的(de)模拟投資組合密切相關。後者是使用(yòng) $G_t$ 對(duì) $R_t$ 的(de)主成分(fēn)回歸以構造其因子模拟投資組合，并通(tōng)過計算(suàn)其平均收益率而得(de)到 $G_t$ 的(de)風險溢價。使用(yòng)主成分(fēn)而非 $R_t$ 中的(de)原始資産是一種正則化(huà)形式。這(zhè)種觀點鼓勵人(rén)們在構造模拟投資組合時(shí)，采用(yòng)機器學習(xí)中的(de)其他(tā)正則化(huà)方法，如嶺回歸和(hé) LASSO 回歸。

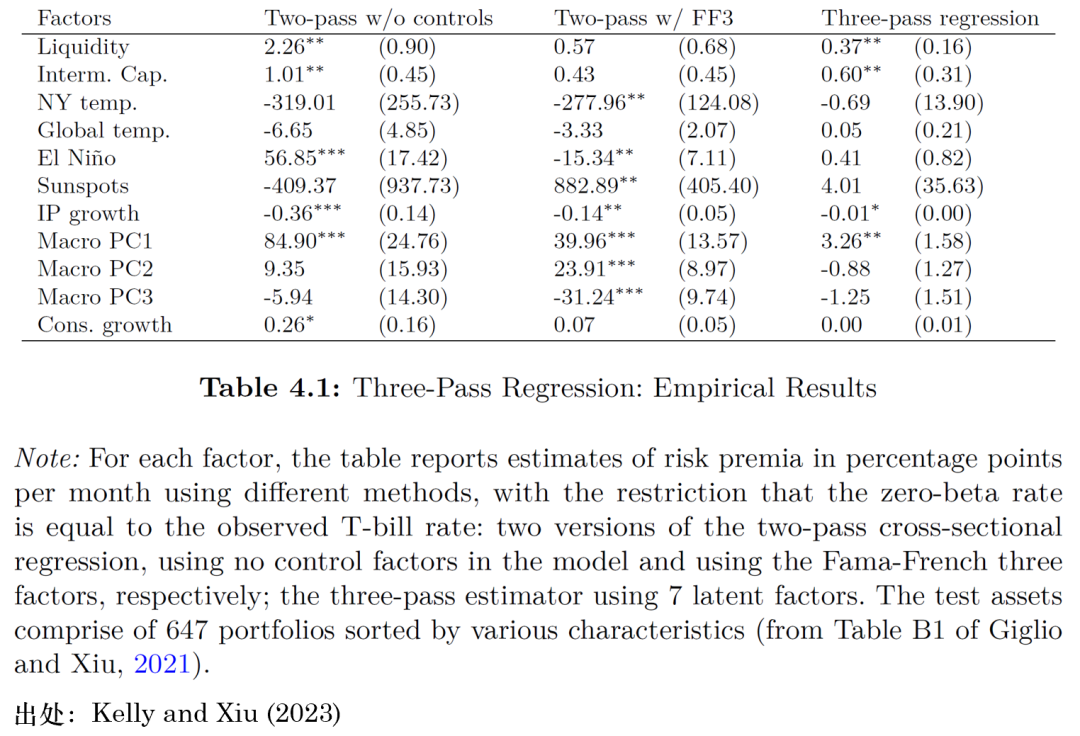
在實證研究方面，表 4.1 彙總了(le)使用(yòng)不同方法對(duì)若幹不可(kě)交易因子的(de)風險溢價估計，其中包括 Ludvigson and Ng (2010) 中的(de)工業生産增長(cháng)的(de) AR(1) 沖擊（IP），以及 279 個(gè)宏觀金融變量的(de)前三個(gè)主成分(fēn)的(de) VAR(1) 沖擊，Pástor and Stambaugh (2003) 的(de)流動性因子，He et al. (2017) 的(de)中介資本因子，Novy-Marx (2014) 的(de)四個(gè)氣象因子，以及 Malloy et al. (2009) 的(de)一個(gè)綜合消費因子。

表格中的(de)結果清晰展示了(le)傳統兩步法回歸中存在的(de)兩個(gè)問題：遺漏變量偏誤以及測量誤差偏誤。兩步法估計量依賴于研究者選擇哪些基準因子作爲控制變量。然而，就這(zhè)方面而言，經濟理(lǐ)論往往無法提供足夠的(de)指引。遺漏控制變量通(tōng)常會導緻風險溢價估計量出現偏誤。以流動性和(hé)中介資本因子爲例，對(duì)于前者而言，當使用(yòng)單變量的(de)兩步法回歸時(shí)，其風險溢價估計值爲每月(yuè) 226 個(gè)基點，而一旦使用(yòng) FF3 因子作爲控制變量，其風險溢價則變爲 57 個(gè)基點；類似地，對(duì)于後者而言，兩種情況下(xià)的(de)風險溢價分(fēn)别爲 101 和(hé) 43 個(gè)基點。

式 (4.5) 也(yě)可(kě)用(yòng)來(lái)分(fēn)析噪聲因子（ $\eta=0$ ）和(hé)弱因子（ $\eta$ 很小）這(zhè)兩類特殊情況，它們的(de)存在往往會影(yǐng)響兩步法回歸中關于因子溢價的(de)推斷（這(zhè)種現象最初由 Kan and Zhang (1999) 提出）。例如，來(lái)自 Novy-Marx (2014) 的(de)四個(gè)因子看上去确實能夠在常規預測回歸檢驗中預測收益率，但它們與股票(piào)市場(chǎng)的(de)經濟聯系似乎無關。盡管如此，使用(yòng) FF3 爲控制變量的(de)兩步法回歸顯示其中三個(gè)因子都有顯著的(de)風險溢價。宏觀因子（例如上述主成分(fēn)或消費增長(cháng)）也(yě)屬于弱因子。三步法能夠解決遺漏變量偏差和(hé)測量誤差問題，這(zhè)是因爲它的(de)第一步估計了(le)隐性因子，并在第二步将它們作爲截面回歸時(shí)的(de)控制變量，最後在第三步通(tōng)過時(shí)序回歸來(lái)消除測量誤差。得(de)益于這(zhè)種穩健性，表 4.1 最後兩列展示的(de)估計值（譯者注：來(lái)自三步法估計量）似乎更具經濟合理(lǐ)性。

4.2.3 PCA 延伸

雖然 PCA 是發現因子的(de)最常見方法，但也(yě)還(hái)存在其他(tā)一些具備獨特特點的(de)拓展。例如，Giglio et al. (2021a) 采用(yòng)矩陣補全來(lái)估計因子模型，以應對(duì)不平衡面闆收益率數據的(de)問題。假設 $\Omega$ 是一個(gè) $N\times T$ 維矩陣，當且僅當 $R_{i,t}$ 不缺失時(shí)， $\Omega$ 中的(de)第 $(i, t)$ 個(gè)元素等于 $1$ 。矩陣補全算(suàn)法解決了(le)以下(xià)凸優化(huà)問題：

$\displaystyle\widehat{X}=\arg\min_X\parallel(R-X)\circ\Omega\parallel^2+\lambda\parallel X\parallel_n,$

其中 $\circ$ 表示哈達瑪乘積（譯者注：即兩個(gè)形狀一樣的(de)矩陣中相同位置的(de)元素相乘）， $\parallel X\parallel_n=\sum_{i=1}^{\min\{N,T\}}\psi_i(X)$ 且 $\psi_i(X)$ 表示 $X$ 的(de)第 $i$ 大(dà)的(de)奇異值， $\lambda$ 則是一個(gè)調優參數。通(tōng)過懲罰 $X$ 奇異值的(de) $\ell_1$ 範數，該算(suàn)法試圖僅使用(yòng)非缺失的(de)元素來(lái)找到 $R$ 的(de)一個(gè)低秩近似。所估計的(de) $\widehat{X}$ 是具有低秩結構的(de) $R$ 的(de)完整矩陣，對(duì)它進行奇異值分(fēn)解便能夠獲得(de)隐性因子以及因子暴露。

标準 PCA 實現方法是對(duì)去均值後的(de)超額收益矩陣 $\bar{R}$ 進行奇異值分(fēn)解。該處理(lǐ)方法通(tōng)過收益率的(de)樣本中心二階矩來(lái)估計隐性因子和(hé) $\beta$ 值。Lettau and Pelger (2020b) 指出，PCA 僅使用(yòng)二階矩的(de)信息導緻了(le)因子模型的(de)估計值并非是有效的(de)（譯者注：即估計量的(de)方差并非最小）。資産定價理(lǐ)論暗示了(le)資産預期收益率和(hé)因子暴露 $\beta$ 之間的(de)關系（例如，基于無條件的(de)歐拉方程 (1.2)）。因此，他(tā)們認爲，更加重視收益數據一階矩中包含的(de)因子暴露信息能夠提高(gāo) PCA 估計量的(de)整體性能。基于該想法，他(tā)們提出了(le)“風險溢價 PCA”（RP-PCA）估計量，該估計量通(tōng)過對(duì)非中心化(huà)的(de)收益率二階矩應用(yòng) PCA 而得(de)到，即 $T^{-1}\sum_{t=1}^{T} R_tR_t^\prime+\lambda(T^{-1}\sum_{t=1}^{T}R_t)(T^{-1}\sum_{t=1}^{T}R_t)^\prime$ ，其中 $\lambda >-1$ 是調優參數。Connor and Korajczyk (1988) 同樣使用(yòng)了(le)非中心化(huà)的(de) PCA，但僅限于 $\lambda = 0$ 的(de)情況，而标準的(de) PCA 則對(duì)應著(zhe) $\lambda = -1$ 的(de)情況。

Lettau and Pelger (2020a) 建立了(le) RP-PCA 的(de)漸近理(lǐ)論，并指出在沒有定價誤差且因子是普遍存在的(de)情況下(xià)，它比 PCA 估計量更有效。雖然标準 PCA 方法對(duì)定價誤差的(de)存在并不敏感，但由于定價誤差存在時(shí)資産預期收益率不再和(hé)因子暴露一一對(duì)應，因此該誤差可(kě)能會導緻 RP-PCA 估計量出現偏移。我們猜測，如果施加了(le)無近似套利的(de)經濟約束 (4.2)，該偏移則是可(kě)以漸近忽略的(de)，因爲在這(zhè)種情況下(xià) $\alpha$ 足夠小，從而不會對(duì)因子及因子暴露的(de)漸近估計産生偏差。

Giglio et al. (2021b) 指出一個(gè)因子的(de)強度取決于測試資産的(de)選擇。如果所有的(de)測試資産都是對(duì)市場(chǎng)暴露爲零的(de)多(duō)空對(duì)沖組合，那麽即便是市場(chǎng)因子也(yě)會被認爲是一個(gè)弱因子。爲了(le)解決風險溢價估計中的(de)弱因子問題，該文提出了(le)一個(gè)基于監督 PCA 來(lái)選擇檢驗資産的(de)方法（如第 3.5.2 節所述）。此外，這(zhè)個(gè)方法可(kě)以被用(yòng)來(lái)檢測随機貼現因子模型中的(de)缺失因子。

4.2.4 有哪些因子？

人(rén)們爲了(le)解釋股票(piào)預期收益率截面差異，已經找到了(le)數百個(gè)潛在的(de)候選因子。然而，其中很多(duō)因子在控制了(le)其他(tā)因子之後便對(duì)資産定價而言沒有增量的(de)解釋力，因而是冗餘的(de)。有些因子甚至自身就是完全無用(yòng)的(de)，沒有任何解釋力。

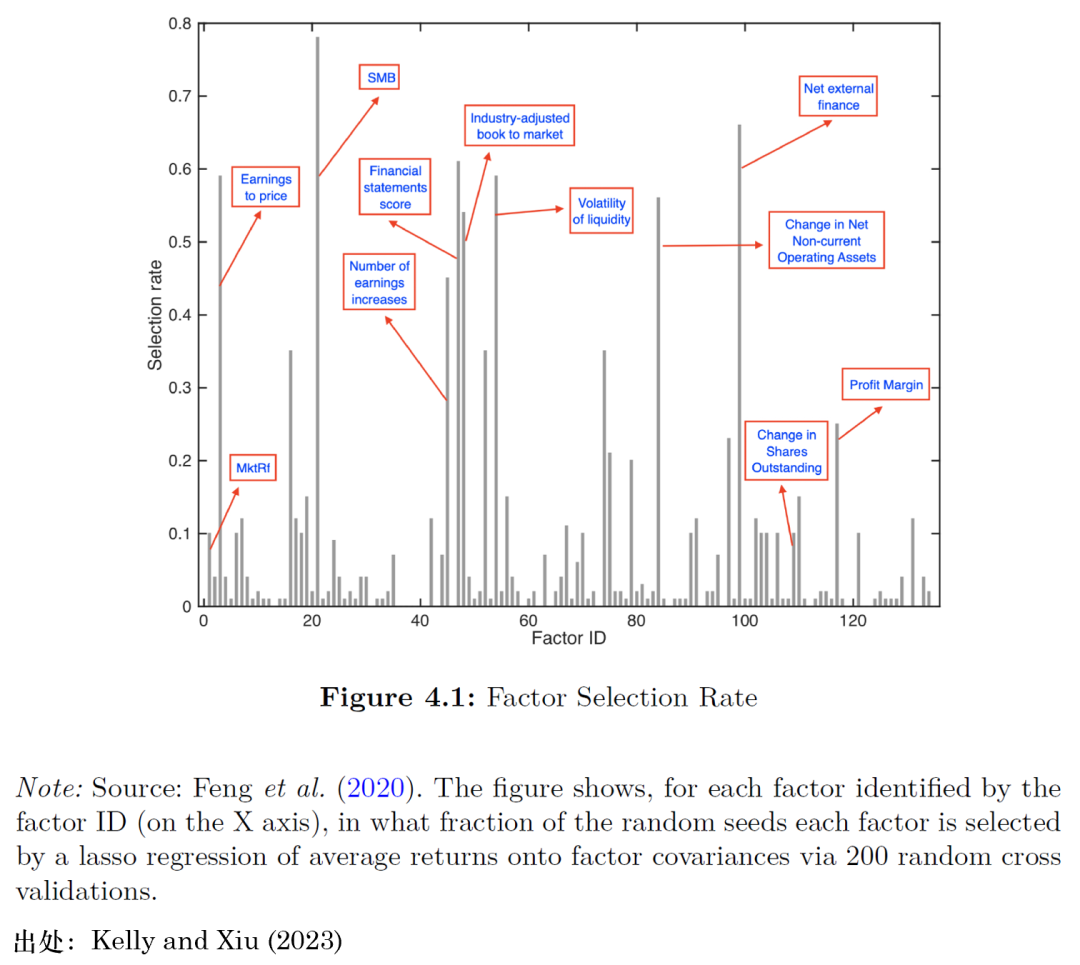
機器學習(xí)方法可(kě)以通(tōng)過降維和(hé)變量選擇來(lái)解決冗餘和(hé)無用(yòng)因子問題。例如，通(tōng)過将平均收益率對(duì)因子協方差進行 LASSO 回歸可(kě)以獲得(de)一個(gè)簡約的(de)因子集，它們能夠在截面上很好地爲資産定價。與此同時(shí)，錯誤選擇也(yě)是難以避免的(de)：過度拟合可(kě)能導緻選出無用(yòng)的(de)因子；相對(duì)解釋力較弱的(de)因子可(kě)能被遺漏；冗餘的(de)因子也(yě)有可(kě)能被選出從而取代真正的(de)因子。Feng et al. (2020) 的(de)發現（圖 4.1）顯示，在交叉驗證時(shí)采用(yòng)不同的(de)随機種子（即随機将樣本數據分(fēn)割爲多(duō)個(gè)子集）會對(duì) LASSO 回歸的(de)結果産生重大(dà)的(de)影(yǐng)響。

Feng et al. (2020) 将 Chernozhukov et al. (2018) 的(de)雙機器學習(xí)框架和(hé)兩步法橫截面回歸相結合，提出了(le)一個(gè)能夠識别與資産定價密切相關的(de)因子的(de)方法，并同時(shí)給出了(le)其估計量的(de)漸近分(fēn)布。通(tōng)過該分(fēn)布，他(tā)們可(kě)以對(duì)這(zhè)些因子進行推斷。

在實證方面，Feng et al. (2020) 遞歸地使用(yòng)他(tā)們的(de)推斷方法，以此區(qū)分(fēn)文獻中介紹的(de)有用(yòng)因子和(hé)無用(yòng)及冗餘因子。他(tā)們的(de)實證發現顯示，如果從 1994 年開始逐年應用(yòng)他(tā)們的(de)方法，那麽在 120 多(duō)個(gè)候選因子中隻有 17 個(gè)因子是有用(yòng)的(de)，而其他(tā)大(dà)多(duō)數因子則是冗餘或無用(yòng)的(de)。

另有文獻從模型不确定性和(hé)模型平均的(de)角度考慮因子模型的(de)選擇問題，相關的(de)研究包括 Avramov et al. (2023) 和(hé) Chib et al. (2023)。Avramov et al. (2023) 認爲，關于夏普比率取值的(de)先驗觀點将左右因子和(hé)預測變量的(de)選擇。總體上，貝葉斯所考慮到的(de)模型不确定性是未來(lái)金融機器學習(xí)領域中一個(gè)有趣的(de)研究方向。

4.3 條件因子模型

前一節重點關注了(le)歐拉方程 (1.2) 的(de)無條件版本（通(tōng)過空集代替信息集 $\mathbb{I}_t$ ，或去掉條件），即因子暴露和(hé)風險價格都是靜态的(de)，不随時(shí)間變化(huà)。通(tōng)常，當我們改變條件信息集時(shí)，因子也(yě)會随之而改變，這(zhè)是因爲資産的(de)條件矩會發生變化(huà)。我們不能完全否定如下(xià)這(zhè)種情況，即當我們去掉條件時(shí)，資産的(de)因子暴露和(hé)預期收益率不會發生變化(huà) —— 在這(zhè)種特殊情況下(xià)，條件和(hé)無條件模型是相同的(de)。然而，實證研究表明(míng)資産的(de)協方差在時(shí)間序列中是高(gāo)度可(kě)預測的(de)，并且大(dà)量的(de)證據表明(míng)資産的(de)預期收益率也(yě)是可(kě)預測的(de)。換句話(huà)說，我們可(kě)以排除“條件靜态”（譯者注：因子暴露和(hé)風險價格不随給定信息集而變化(huà)）這(zhè)一特殊情況。

是選擇條件還(hái)是無條件模型？這(zhè)是在研究收益率因子模型時(shí)要考慮的(de)問題。我們的(de)觀點是，研究者都應盡可(kě)能努力構建一個(gè)有效的(de)條件模型。條件模型往往目标遠(yuǎn)大(dà) —— 它們描述了(le)資産價格的(de)狀态依賴性，從而更精細地捕捉了(le)市場(chǎng)的(de)行爲。然而，提出條件模型的(de)要求也(yě)更高(gāo)，它需要研究者提供相關數據來(lái)總結當前的(de)條件。這(zhè)種條件信息集涉及的(de)方面可(kě)能非常廣泛，并且可(kě)能需要更豐富的(de)參數化(huà)模型來(lái)捕捉微妙的(de)條件行爲。當相關的(de)條件信息不可(kě)用(yòng)時(shí)，使用(yòng)簡單的(de)無條件模型，研究者在無需了(le)解詳細的(de)市場(chǎng)動态的(de)情況下(xià)便能夠理(lǐ)解基本的(de)資産行爲。因此，早期關于收益率因子分(fēn)析的(de)文獻大(dà)多(duō)使用(yòng)了(le)無條件模型（如前一節所述）。在本節中，我們将討(tǎo)論的(de)重點放在條件模型的(de)構建上。

與式 (4.1) 類似，向量形式的(de)條件隐性因子模型爲

$\displaystyle R_{t+1}=\alpha_t+\beta_tF_{t+1}+\epsilon_{t+1},~~~~~~(4.7)$

其中因子暴露和(hé)定價誤差均随條件信息集 $\mathbb{I}_t$ 變化(huà)。

4.3.1 IPCA

如不加入額外的(de)約束，模型則會因爲式 (4.7) 右側的(de)自由度太高(gāo)而無法被識别。Kelly et al. (2019) 利用(yòng)工具變量主成分(fēn)分(fēn)析（IPCA）将因子暴露（以及資産的(de)定價錯誤）和(hé)觀測變量聯系在一起，取得(de)了(le)一定的(de)進展。IPCA 模型的(de)形式爲：

$\displaystyle R_{t+1}=\underbrace{Z_t\Gamma_{\alpha}}_{\alpha_t} + \underbrace{Z_t\Gamma_{\beta}}_{\beta_t}F_{t+1}+\epsilon_{t+1},~~~~~~(4.8)$

其中 $N\times L$ 矩陣 $Z_t$ 表示 $N$ 個(gè)資産在L個(gè)可(kě)觀測特征（“工具變量”）的(de)取值。 $K\times 1$ 維向量 $F_{t+1}$ 表示隐性因子。Harvey and Ferson (1999) 以及近期的(de) Gagliardini et al. (2016) 也(yě)通(tōng)過可(kě)觀測變量的(de)時(shí)變函數爲因子暴露建模，但他(tā)們的(de)因子是完全可(kě)觀測的(de)。

IPCA 模型的(de)核心是其對(duì) $\beta_t$ 的(de)設定。首先最重要的(de)是，時(shí)變的(de)工具變量直接将條件性引入到條件因子暴露中。更爲根本的(de)是，納入工具變量允許多(duō)因子模型受到更多(duō)數據的(de)影(yǐng)響，這(zhè)與僅從收益率數據估算(suàn)因子結構的(de)無條件隐性因子方法（如 PCA）有所不同。此外，将因子暴露錨定到可(kě)觀察的(de)變量上，使得(de)我們在識别多(duō)因子模型時(shí)通(tōng)過數據部分(fēn)替代未識别的(de)參數。

模型中 $L\times K$ 維矩陣 $\Gamma_{\beta}$ 将潛在大(dà)量的(de)公司特征（ $L$ 維）映射到少數幾個(gè)風險因子（ $K$ 維）的(de)暴露上。當估計 $\Gamma_{\beta}$ 時(shí)，我們的(de)目标是尋找公司特征的(de)少數幾個(gè)線性組合，以使它們盡可(kě)能地代表隐性的(de)因子暴露結構。爲了(le)更好地理(lǐ)解這(zhè)一點，試想一下(xià) $\Gamma_{\beta}$ 是一個(gè) $L$ 維的(de)單位矩陣的(de)情況。這(zhè)時(shí)，容易證明(míng) $F_t$ 包含了(le) $L$ 個(gè)隐性因子（它們的(de)收益率正比于 $R_{t+1}^\prime Z_t$ ）且特征決定了(le)資産對(duì)這(zhè)些因子的(de)暴露值。這(zhè)不禁讓人(rén)想起 Rosenberg (1974) 以及 MSCI Barra 多(duō)因子模型（Barra 模型是業界一個(gè)常用(yòng)的(de)風險因子模型）。在 Barra 模型中， $Z_t$ 包括了(le)幾十個(gè)公司特征和(hé)行業指标。當特征 $L$ 的(de)數量很大(dà)時(shí)，自由參數的(de)數量等于因子實現值的(de)數量 $\{F_t\}$ ，或 $L\times T$ ，這(zhè)通(tōng)常比樣本數要多(duō)。Barra 模型中的(de)因子存在顯著的(de)冗餘（少量的(de)主成分(fēn)能夠捕獲了(le)它們的(de)大(dà)部分(fēn)共同變化(huà)），這(zhè)表明(míng)它的(de)過度參數化(huà)以及非有效性。

IPCA 通(tōng)過對(duì)特征空間降維來(lái)解決這(zhè)個(gè)問題。如果許多(duō)公司特征都關于股票(piào)風險敞口提供了(le)帶噪聲的(de)信号，那麽将它們聚合成線性組合能夠在剝離出信号的(de)同時(shí)一并抵消掉噪聲。

資産風格遷移問題，例如股票(piào)從小市值變成大(dà)市值或者從成長(cháng)股變爲價值股，對(duì)使用(yòng)簡單的(de)時(shí)間序列方法研究個(gè)股條件預期收益率模型提出了(le)極大(dà)的(de)挑戰。對(duì)此，常規的(de)解決方法是構造一些投資組合，每個(gè)組合中的(de)資産在特定公司特征上的(de)平均值在時(shí)序上相對(duì)穩定。然而，如果我們需要用(yòng)多(duō)個(gè)公司特征來(lái)準确描述資産時(shí)，上述方法就變得(de)不切實際。IPCA 的(de)解決方案是将因子暴露（ $\beta$ ）視爲影(yǐng)響股票(piào)風險和(hé)收益率的(de)公司特征的(de)函數。IPCA 通(tōng)過資産的(de)因子暴露來(lái)跟蹤資産風格遷移，而因子暴露又由公司特征而确定。這(zhè)使得(de)模型能夠根據特征的(de)取值來(lái)識别資産，不再需要研究者手動将資産劃分(fēn)到不同的(de)投資組合。因此，該模型無需通(tōng)過構造特設（ad-hoc）的(de)投資組合便能夠處理(lǐ)高(gāo)維度的(de)資産體系（即個(gè)股）。

最後，式 (4.8) 所示的(de) IPCA 設定還(hái)考慮了(le)這(zhè)樣一種可(kě)能，即（公司）特征代表 $\alpha$ 而非 $\beta$ 。傳統的(de)資産定價模型假設資産之間的(de)預期收益率差異僅僅是歸因于其風險敞口的(de)差異。然而，一旦 $L\times 1$ 維系數向量 $\Gamma_{\alpha}$ 不爲零，則意味著(zhe)股票(piào)層面的(de)特征能夠以一種和(hé)風險暴露對(duì)應之外的(de)方式來(lái)預測收益率（譯者注：即預測風險暴露之外的(de)超額收益率）。IPCA 在控制住公司特征對(duì)因子暴露的(de)作用(yòng)的(de)前提下(xià)，以盡可(kě)能解釋資産預期收益率截面差異爲目标，通(tōng)過公司特征的(de)線性函數（ $\Gamma_{\alpha}$ ）來(lái)估計 $\alpha$ 。如果特征和(hé)資産平均收益率的(de)關系與特征與風險因子暴露之間的(de)關系存在差異（譯者注：即預期收益不僅僅由對(duì)風險因子的(de)暴露決定），IPCA 便會得(de)到一個(gè)非零的(de)估計 $\Gamma_{\alpha}$ ，從而識别出錯誤定價（即因持有資産而獲得(de)的(de)與資産系統性風險敞口無關的(de)額外補償）。

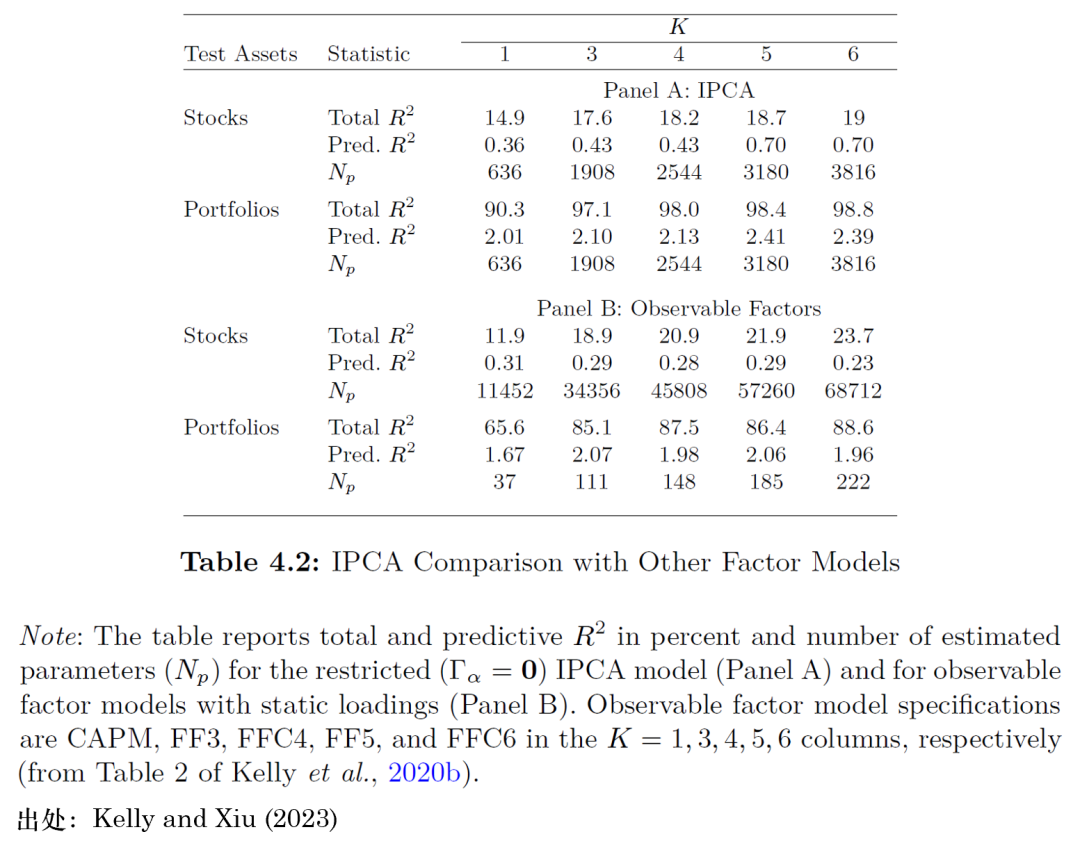
表 4.2 将使用(yòng)不同數量隐性因子的(de) IPCA 模型（面闆A）與文獻中的(de)其他(tā)主要多(duō)因子模型進行了(le)比較。第一組比較模型包括預先指定的(de)可(kě)觀察因子，并逐一使用(yòng)資産進行時(shí)間序列回歸這(zhè)一傳統方法進行估計。K=1 表示 CAPM 模型，K=3 表示包括市場(chǎng)、SMB 以及 HML 的(de) Fama and French (1993) 三因子模型（以下(xià)簡稱“FF3”），K=4 表示 Carhart (1997，“FFC4”) 模型，它在 FF3 模型中加入了(le)動量因子 MOM，K=5 代表 Fama and French (2015，“FF5”) 五因子模型，它在 FF3 模型中加入了(le)盈利 RMW 和(hé)投資 CMA 因子，K=6（“FFC6”）則在 FF5 之上加入了(le)動量 MOM 因子。在表 4.2 的(de)結果中，所有 IPCA 模型都是在施加 $\Gamma_{\alpha} = 0$ 的(de)約束下(xià)而估計得(de)到，且所有時(shí)序回歸中都沒有包含截距項。

表 4.2 報告了(le)基于同期因子已實現收益率計算(suàn)的(de)總體 $R^2$ 、預測性 $R^2$ （用(yòng)因子收益率均值代替已實現值）以及每個(gè)模型中所需估計參數的(de)數量（ $N_p$ ）。我們同時(shí)彙報了(le)模型對(duì)個(gè)股以及基于特征構造的(de)投資組合的(de)定價表現。表中的(de)統計數據是樣本内的(de)計算(suàn)結果。當考慮股票(piào)時(shí)，基于可(kě)觀察因子的(de)模型的(de)總體 $R^2$ 略高(gāo)于 IPCA 模型。然而，爲了(le)實現這(zhè)一點，基于可(kě)觀察因子的(de)模型所需要估計的(de)參數數量遠(yuǎn)遠(yuǎn)超過 IPCA 模型。在這(zhè)個(gè)包含 11452 支股票(piào)、37 個(gè)工具變量和(hé) 599 個(gè)月(yuè)的(de)樣本中，可(kě)觀察因子模型所需估計的(de)參數是 IPCA 模型的(de) 18 倍（ $\approx 11452/(37 + 599)$ ）。換言之，IPCA 模型與主流多(duō)因子模型在刻畫(huà)個(gè)股系統性風險方面的(de)表現十分(fēn)接近，而 IPCA 模型将需要估計的(de)參數個(gè)數減少了(le)将近 95%。與此同時(shí)，IPCA 模型比可(kě)觀測因子模型提供了(le)關于股票(piào)風險補償更加準确的(de)刻畫(huà)，一如預測性 $R^2$ 所表明(míng)的(de)那樣。對(duì)于基于特征構造的(de)投資組合而言，無論是總體 $R^2$ 還(hái)是預測性 $R^2$ ，IPCA 模型都優于可(kě)觀測因子模型。

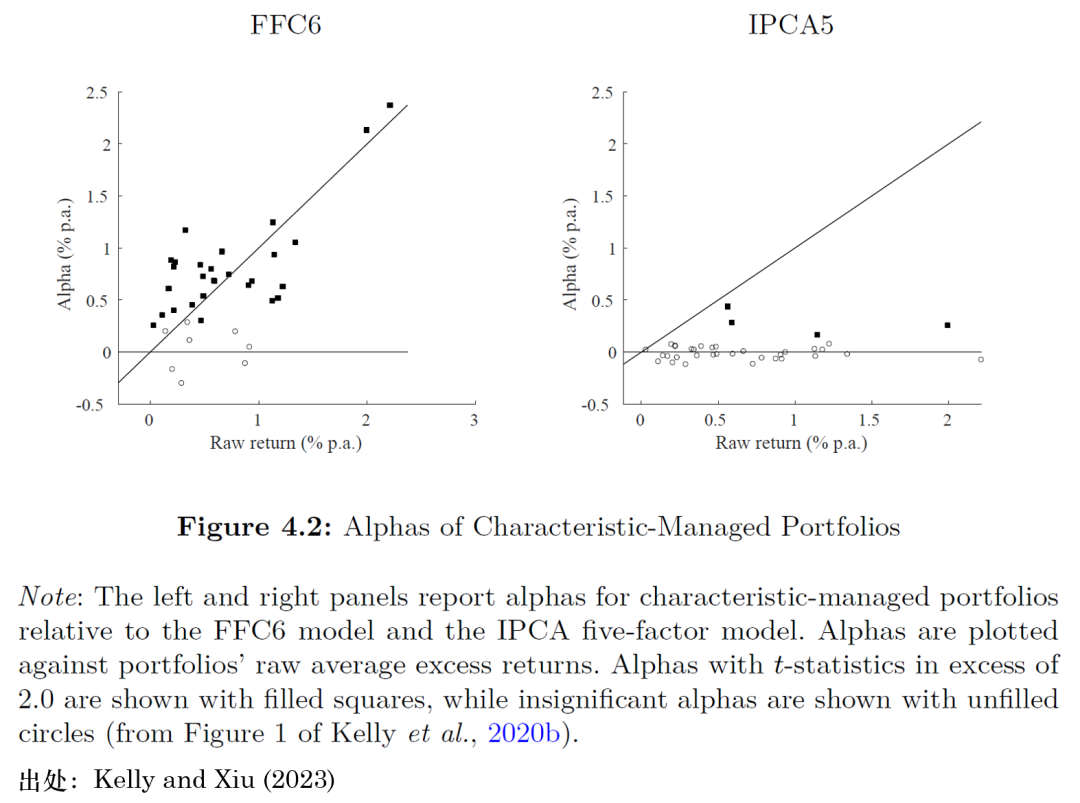
圖 4.2 比較了(le)兩類模型對(duì) 37 個(gè)基于特征構造的(de)“異象”投資組合的(de)平均定價誤差。在左側的(de)子圖中，縱坐(zuò)标是這(zhè)些異象組合相對(duì)于 FFC6 模型的(de)超額收益率 $\alpha$ ，橫坐(zuò)标是其原始的(de)平均收益率，可(kě)以看到它們和(hé) 45 度線相重疊（譯者注：說明(míng) FFC6 無法解釋這(zhè)些異象）。圖中實心正方形表示 t-statistic 超過 2.0 的(de) $\alpha$ ，空心圓圈表示不顯著的(de) $\alpha$ 。當使用(yòng) FFC6 作爲定價模型時(shí)，有 29 個(gè)特征投資組合獲得(de)了(le)顯著的(de) $\alpha$ 。這(zhè)些 $\alpha$ 圍繞著(zhe) 45 度線排列，表明(míng)它們的(de)平均收益率無法被 FFC6 模型中的(de)可(kě)觀測因子解釋。右側的(de)子圖展示了(le)包含五個(gè)隐性因子的(de) IPCA 模型的(de)情況。此時(shí)，僅有 4 個(gè)特征投資組合的(de)條件 $\alpha$ 顯著不爲零（但經濟意義很小）。基于上述結果，我們可(kě)以得(de)出如下(xià)結論：相對(duì)于具有可(kě)觀察因子的(de)資産定價模型而言，包含隐性因子的(de) IPCA 模型對(duì)一系列股票(piào)投資組合的(de)定價效果更好。

上述 IPCA 框架已被應用(yòng)于多(duō)種市場(chǎng)的(de)截面資産定價問題之中，包括國際股票(piào)（Langlois 2021; Windmueller 2022）、公司債券（Kelly et al. forthcoming）、股票(piào)指數期權（Büchner and Kelly 2022）、特定單一股票(piào)期權（Goyal and Saretto 2022）以及貨币（Bybee et al. 2023a）市場(chǎng)。此外，它還(hái)被用(yòng)來(lái)分(fēn)析價格趨勢信号的(de)盈利能力（Kelly et al. 2021）以及叙事資産定價模型（Bybee et al. forthcoming）。

參考文獻

Avramov, D., S. Cheng, L. Metzker, and S. Voigt (2023). Integrating factor models. Journal of Finance 78(3), 1593–1646.

Bai, J. (2003). Inferential theory for factor models of large dimensions. Econometrica 71(1), 135–171.

Bai, J. and S. Ng (2002). Determining the number of factors in approximate factor models. Econometrica 70(1), 191–221.

Büchner, M. and B. T. Kelly (2022). A factor model for option returns. Journal of Financial Economics 143(3), 1140–1161.

Bybee, L., B. T. Kelly, and Y. Su. (forthcoming). Narrative asset pricing: Interpretable systematic risk factors from news text. Review of Financial Studies.

Chamberlain, G. and M. Rothschild (1983). Arbitrage, factor structure, and mean-variance analysis on large asset markets. Econometrica 51(5), 1281–1304.

Chernozhukov, V., D. Chetverikov, M. Demirer, E. Duflo, C. Hansen, W. K. Newey, and J. Robins (2018). Double/debiased machine learning for treatment and structure parameters. The Econometrics Journal 21(1), C1–C68.

Chib, S., L. Zhao, and G. Zhou (2023). Winners from winners: A tale of risk factors. Management Science.

Connor, G. and R. A. Korajczyk (1986). Performance measurement with the arbitrage pricing theory: A new framework for analysis. Journal of Financial Economics 15(3), 373–394.

Connor, G. and R. A. Korajczyk (1988). Risk and return in an equilibrium APT: Application of a new test methodology. Journal of Financial Economics 21(2), 255–289.

Feng, G., S. Giglio, and D. Xiu (2020). Taming the factor zoo: A test of new factors. Journal of Finance 75(3), 1327–1370.

Gagliardini, P., E. Ossola, and O. Scaillet (2016). Time-varying risk premium in large cross-sectional equity data sets. Econometrica 84(3), 985–1046.

Geweke, J. and G. Zhou (1996). Measuring the pricing error of the arbitrage pricing theory. Review of Financial Studies 9(2), 557–587.

Giglio, S., B. T. Kelly, and D. Xiu (2022a). Factor models, machine learning, and asset pricing. Annual Review of Financial Economics 14, 1–32.

Giglio, S., Y. Liao, and D. Xiu (2021a). Thousands of alpha tests. Review of Financial Studies 34(7), 3456–3496.

Giglio, S. and D. Xiu (2021). Asset pricing with omitted factors. Journal of Political Economy 129(7), 1947–1990.

Giglio, S., D. Xiu, and D. Zhang (2021b). Test assets and weak factors. Tech. rep. Yale University and University of Chicago.

Goyal, A. and A. Saretto (2022). Are equity option returns abnormal? IPCA says No. Working paper.

Harvey, C. R. and W. E. Ferson (1999). Conditioning variables and the cross-section of stock returns. Journal of Finance 54(4), 1325–1360.

He, Z., B. T. Kelly, and A. Manela (2017). Intermediary asset pricing: New evidence from many asset classes. Journal of Financial Economics 126(1), 1–35.

Huberman, G. (1982). A simple approach to arbitrage pricing theory. Journal of Economic Theory 28(1), 183–191.

Ingersoll, J. E. (1984). Some results in the theory of arbitrage pricing. Journal of Finance 39(4), 1021–1039.

Kelly, B. T., T. Moskowitz, and S. Pruitt (2021). Understanding momentum and reversal. Journal of Financial Economics 140(3),726–743.

Kelly, B. T., D. Palhares, and S. Pruitt (forthcoming). Modeling corporate bond returns. Journal of Finance.

Kelly, B. T., S. Pruitt, and Y. Su (2019). Characteristics are covariances: A unified model of risk and return. Journal of Financial Economics 134(3), 501–524.

Kozak, S., S. Nagel, and S. Santosh (2018). Interpreting factor models. Journal of Finance 73(3), 1183–1223.

Lettau, M. and M. Pelger (2020a). Estimating latent asset-pricing factors. Journal of Econometrics 218, 1–31.

Lettau, M. and M. Pelger (2020b). Factors that fit the time series and cross-section of stock returns. Review of Financial Studies 33(5), 2274–2325.

Ludvigson, S. C. and S. Ng (2010). A factor analysis of bond risk premia”. In: Handbook of Empirical Economics and Finance. Ed. By A. Ulah and D. E. A. Giles. Vol. 1. Chapman and Hall, Boca Raton, FL. Chap. 12. 313–372.

Malloy, C. J., T. J. Moskowitz, and A. Vissing-Jorgensen (2009). Longrun stockholder consumption risk and asset returns. Journal of Finance 64(6), 2427–2479.

Novy-Marx, R. (2014). Predicting anomaly performance with politics, the weather, global warming, sunspots, and the stars. Journal of Financial Economics 112(2), 137–146.

Pástor, L. and R. F. Stambaugh (2003). Liquidity risk and expected stock returns. Journal of Political Economy 111(3), 642–685.

Pukthuanthong, K., R. Roll, and A. Subrahmanyam (2019). A protocol for factor identification. Review of Financial Studies 32(4), 1573–1607.

Rosenberg, B. (1974). Extra-market components of covariance in security returns. Journal of Financial and Quantitative Analysis 9(2), 263–274.

Ross, S. A. (1976). The arbitrage theory of capital asset pricing. Journal of Economic Theory 13(3), 341–360.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。

合格投資者聲明(míng)

Risk-Return Tradeoffs (I)