Ledoit and Wolf 的(de)協方差矩陣收縮之旅

發布時(shí)間：2023-11-22 | 來(lái)源: 川總寫量化(huà)

作者：石川

摘要：本文簡要且有側重地回顧 Ledoit 和(hé) Wolf 兩位在協方差估計方面多(duō)年的(de)嘗試。

協方差矩陣是資産配置的(de)重要輸入之一；對(duì)它的(de)準确估計對(duì)于求解權重的(de)最優化(huà)問題至關重要。然而衆所周知的(de)是，樣本協方差矩陣并非一個(gè)很好的(de)估計量（estimator），尤其是在收益率的(de)期數 $T$ 并非遠(yuǎn)遠(yuǎn)超過資産的(de)個(gè)數 $N$ 的(de)情況下(xià)。

我們以 Frobenius norm 來(lái)衡量兩個(gè)矩陣的(de)差距。對(duì)于矩陣 $A$ 和(hé) $B$ 來(lái)說，其定義爲：

$\displaystyle ||A-B||_{F}=\sqrt{\sum_{i,j}|a_{ij}-b_{ij}|^2},$

其中 $a_{ij}$ 和(hé) $b_{ij}$ 分(fēn)别爲 $A$ 和(hé) $B$ 中第 $i$ 行第 $j$ 列的(de)元素。就協方差估計而言，我們希望估計量和(hé)真實協方差矩陣之間的(de) Frobenius norm 越小越好。

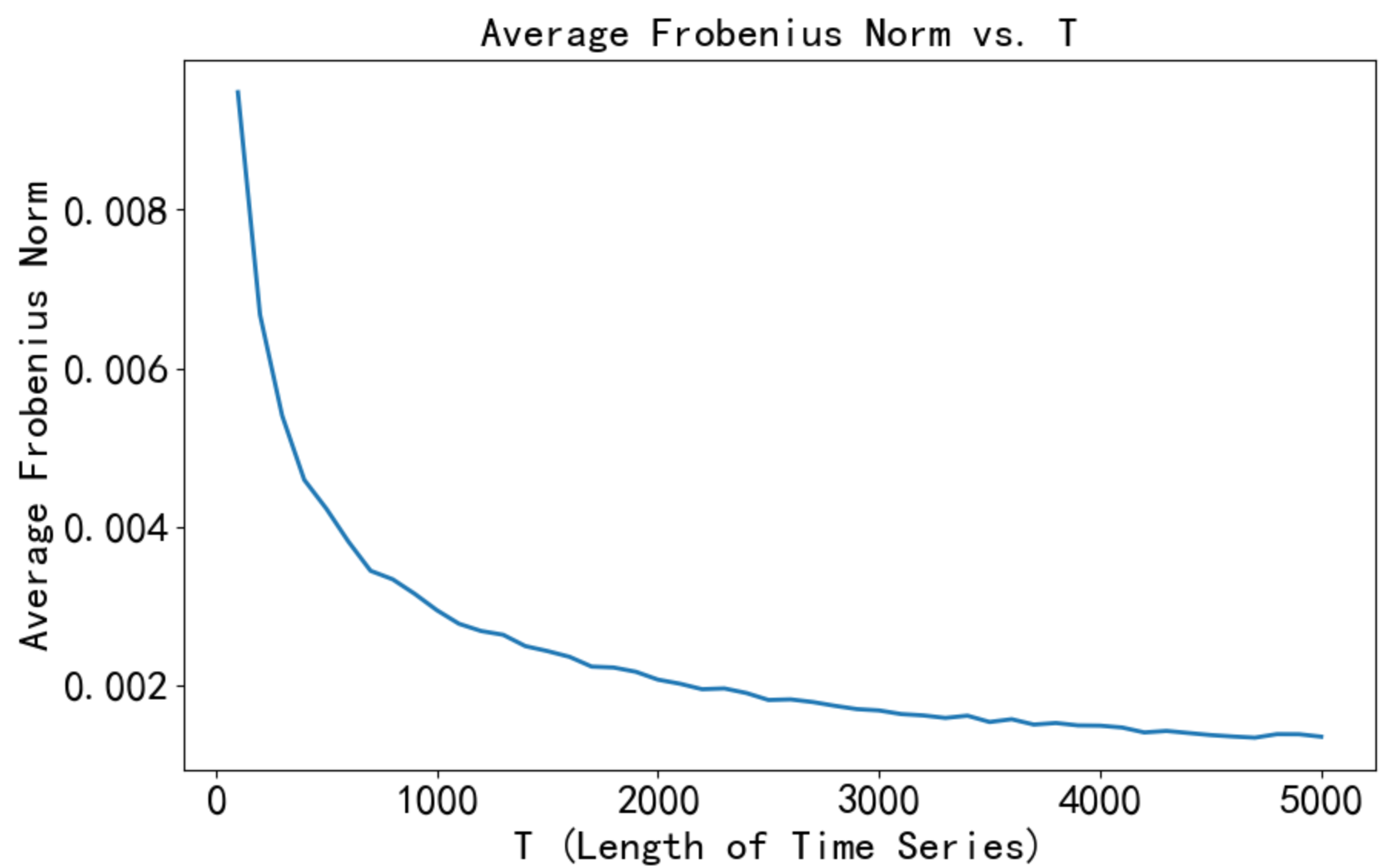
下(xià)面假設 DGP 已知并通(tōng)過模拟說明(míng) $T$ 和(hé) $N$ 的(de)關系如何影(yǐng)響上述差異。爲此，令 $N=50$ ，并且收益率滿足均值爲零的(de)多(duō)元正态分(fēn)布，并随機生成一個(gè)正定的(de)協方差矩陣作爲真實的(de)協方差矩陣。之後，令 $T$ 的(de)取值從 100 到 5000（步長(cháng) 100），且對(duì)每個(gè) $T$ 進行 $M=1000$ 次模拟。在每次模拟中，計算(suàn)樣本協方差矩陣和(hé)真實協方差矩陣的(de) Frobenius norm，并取 1000 次的(de)均值作爲該 $T$ 下(xià)的(de)誤差。結果如下(xià)圖所示。它意味著(zhe)，對(duì)于區(qū)區(qū) $N=50$ 個(gè)标的(de)，我們也(yě)需要 $T=5000$ 期的(de)數據（對(duì)于日頻(pín)就是差不多(duō) 20 年）才能比較放心的(de)使用(yòng)樣本協方差矩陣。

但顯然，這(zhè)種數據量的(de)需求是奢侈的(de)；而且實際資産配置中，标的(de)個(gè)數也(yě)可(kě)能遠(yuǎn)遠(yuǎn)超過 50。因此，我們需要更好的(de)協方差矩陣估計量（當然，如果你的(de)标的(de)個(gè)數很少，比如配置因子且因子個(gè)數 < 10，那麽使用(yòng)更複雜(zá)的(de)估計量取代樣本協方差矩陣所能獲得(de)的(de)益處比較有限）。這(zhè)就要請出今天的(de)主角：Olivier Ledoit 和(hé) Michael Wolf。這(zhè)兩位在過去 15 到 20 年的(de)時(shí)間裏緻力于利用(yòng)收縮技術（shrinkage）提出更好的(de)協方差矩陣估計量，其研究範圍從線性收縮到非線性收縮，從靜态模型到動态模型，從 empirical Bayes 到多(duō)因子模型。

今天這(zhè)篇文章(zhāng)就來(lái)（非常）簡要地回顧一下(xià)。需要說明(míng)的(de)是，本文涉及的(de)重點自然反映了(le)我個(gè)人(rén)的(de)偏好（比如我會聚焦在靜态模型的(de)情況，即假設不同時(shí)刻的(de)收益率滿足 IID），而希望了(le)解進一步信息的(de)小夥伴請參考兩位作者自己寫的(de)綜述文章(zhāng) Ledoit and Wolf (2022)。此外，就協方差矩陣估計量而言，除了(le)這(zhè)兩位外，學界還(hái)有大(dà)量重要發現，但它們并非本文關注的(de)重點（again，再次反映了(le)我個(gè)人(rén)的(de)偏好）。

先說說線性收縮。我接觸到 Ledoit 和(hé) Wolf 這(zhè)兩位就是從他(tā)們把樣本協方差矩陣往單位矩陣收縮（Ledoit and Wolf 2004b）開始。他(tā)們兩位受到 James and Stein (1961) 将樣本均值向零收縮的(de)啓發，提出将樣本協方差矩陣向單位矩陣（的(de)某個(gè)縮放版本）收縮。

令 $X_T$ 表示 $T\times N$ 維收益率矩陣（爲了(le)簡化(huà)下(xià)面的(de)數學表達，假設它每一列都是 demean 的(de)）。因此，樣本協方差矩陣爲

$\displaystyle S_T=\frac{1}{T}X_T^\prime X_T.$

将其向單位矩陣（的(de)某個(gè)縮放版本）收縮，由此得(de)出估計量

$\displaystyle\hat{\Sigma}_T=w\mu_T\mathbb{I}_T+(1-w)S_T,$

其中 $w$ 是最優縮放系數， $\mu_T\mathbb{I}_T$ 爲縮放的(de)目标（它表示單位矩陣乘以某個(gè)系數）。系數 $\mu_T$ 是真實協方差矩陣 $\Sigma_T$ 對(duì)角線元素的(de)均值（即所有資産方差的(de)均值），實際使用(yòng)中可(kě)以通(tōng)過樣本方差估計。因此，上述估計量的(de)含義就是把樣本協方差矩陣中對(duì)角線上的(de)元素向其均值收縮。

上述線性收縮方法後來(lái)在很多(duō)領域得(de)到了(le)應用(yòng)。不過對(duì)于金融數據而言，人(rén)們期望盡可(kě)能利用(yòng)金融數據的(de)實際特性來(lái)決定收縮的(de)目标（記爲 $F_T$ ），以取代 $\mu_T\mathbb{I}_T$ ，即

$\displaystyle\hat{\Sigma}_T=wF_T+(1-w)S_T.$

因此，上一節的(de)一個(gè)自然的(de)延伸就是尋找其他(tā) $F_T$ 。和(hé)使用(yòng)單位矩陣作爲收縮目标相比，這(zhè)些延伸可(kě)以理(lǐ)解爲從數據出發來(lái)确定 $F_T$ ，因而得(de)到的(de)估計量可(kě)以被視爲經驗貝葉斯估計量。

在這(zhè)方面，一個(gè)自然的(de)想法是利用(yòng) CAPM 模型。如果 CAPM 成立，那麽資産超額收益率和(hé)市場(chǎng)組合的(de)超額收益率滿足

$r_{it}=\alpha_i+\beta_{i}r_{mt}+e_{it},$

其中 $r_{it}$ 和(hé) $r_{mt}$ 分(fēn)别表示資産 $i$ 和(hé)市場(chǎng)組合的(de)超額收益率。利用(yòng)該單因子模型，我們可(kě)以把資産的(de)協方差矩陣表述爲

$\displaystyle\Sigma_T=\sigma_m^2\beta_T\beta_T^\prime+\Delta_T,$

其中 $\sigma_m^2$ 是市場(chǎng)組合的(de)方差， $\Delta_T$ 是一個(gè)對(duì)角陣，表示随機擾動的(de)方差。通(tōng)過上述關系，我們可(kě)以通(tōng)過樣本數據來(lái)估計相應的(de)量，并得(de)到對(duì)應的(de)收縮對(duì)象 $F_T$ 。Ledoit and Wolf (2003) 對(duì)使用(yòng) CAPM 來(lái)确定 $F_T$ 進行了(le)分(fēn)析。

此外，考慮到 CAPM 并不是描述資産收益率的(de)完美(měi)模型，我們也(yě)可(kě)以進行其他(tā)嘗試。比如，Ledoit and Wolf (2004a) 假設所有資産的(de)相關系數相同，并定義 $F_T$ 如下(xià)

$\displaystyle f_{ij}=\sqrt{\sigma_i\sigma_j}\rho,$

其中 $\sigma_i$ 和(hé) $\sigma_j$ 分(fēn)别爲資産 $i$ 和(hé) $j$ 的(de)标準差， $\rho$ 爲共同的(de)相關系數，在實際中可(kě)以通(tōng)過所有資産兩兩相關系數的(de)均值估計。

再來(lái)說說非線性收縮。爲了(le)便于理(lǐ)解，讓我們從譜分(fēn)解（特征分(fēn)解）的(de)角度重述一下(xià)向單位矩陣收縮的(de)情況，即

$\displaystyle\hat{\Sigma}_T=w\mu_T\mathbb{I}_T+(1-w)S_T.$

不難看出，該估計量等價于先對(duì)樣本協方差矩陣做(zuò)特征分(fēn)解，然後再對(duì)由特征值構造的(de)對(duì)角陣進行相同程度的(de)收縮，即

$\displaystyle\hat{\Sigma}_T=U_T\Delta^\star_T U_T^\prime,$

其中 $U_T$ 是特征向量矩陣，而對(duì)角陣 $\Delta^\star_T$ 中的(de)元素爲 $\delta^\star_{T,i}=w\mu_T+(1-w)\lambda_{T,i}$ 。換句話(huà)說，爲了(le)得(de)到 $\hat{\Sigma}_T$ ，我們把每個(gè)原始特征值 $\lambda_{T,i}$ 以同樣的(de)收縮強度（ $w$ ）往 $\mu_T$ 收縮，然後再利用(yòng)特征向量來(lái)計算(suàn) $\hat{\Sigma}_T$ 即可(kě)。回顧一下(xià)， $\mu_T$ 是所有資産方差的(de)均值，而所有資産的(de)方差之和(hé)等于特征值之和(hé)，因此 $\mu_T$ 也(yě)是特征值的(de)均值。所以上述收縮背後的(de)邏輯就是讓特征值向其均值靠攏。

有了(le)這(zhè)個(gè)鋪墊，就不難理(lǐ)解非線性收縮，即對(duì)不同的(de)特征值進行不同程度的(de)收縮，即通(tōng)過某些方法最優的(de)确定 $\Delta^\star_T$ 中對(duì)角線的(de)元素。這(zhè)背後的(de)數學十分(fēn)複雜(zá)，感興趣的(de)小夥伴可(kě)查閱 Ledoit and Wolf (2015, 2020) 等。

最後，我們再來(lái)簡要介紹一下(xià)利用(yòng)多(duō)因子模型來(lái)構造協方差矩陣估計量。在這(zhè)方面，一個(gè)自然的(de)想法是延伸上面的(de) CAPM，轉而使用(yòng)多(duō)因子模型構造目标 $F_T$ ，然後進行某種收縮。但是兩位作者研究發現這(zhè)條路并不是很好走，尤其是當考慮動态模型的(de)情況時(shí)。爲此，他(tā)們采取了(le)直接基于多(duō)因子模型來(lái)估計協方差矩陣的(de)方法（例如，Barra）。

在這(zhè)方面，De Nard, Ledoit, and Wolf (2021) 同時(shí)考慮了(le)靜态和(hé)動态模型。爲了(le)簡化(huà)，我們以靜态模型爲例（即 factor loading 不随時(shí)間變化(huà)）。假設資産超額收益率滿足某個(gè)多(duō)因子模型，則其協方差矩陣可(kě)以表述爲（非常類似 CAPM 的(de)情況，隻不過拓展到多(duō)因子）

$\displaystyle\Sigma=B^\prime\Sigma_f B+\Sigma_u,$

其中 $B$ 是因子暴露矩陣， $\Sigma_f$ 是因子協方差矩陣， $\Sigma_u$ 是随機擾動的(de)方差矩陣。在實際使用(yòng)中，我們需要通(tōng)過樣本數據估計因子暴露、因子收益率以及随機擾動。由于因子的(de)個(gè)數往往很低，因此分(fēn)析的(de)重點是估計 $\Sigma_u$ 。De Nard, Ledoit, and Wolf (2021) 給出了(le) $\Sigma_u$ 的(de)非線性收縮估計量。

在估計 $\Sigma_u$ 時(shí)，關于它是否是對(duì)角陣的(de)假設會在一定程度上影(yǐng)響最終 $\hat{\Sigma}_T$ 估計量的(de)結果。在 Ross 最早提出 APT 的(de)時(shí)候，他(tā)考慮的(de)是精确（exact）因子模型，即不同資産的(de)随機擾動不相關、 $\Sigma_u$ 是對(duì)角陣。不過後來(lái)人(rén)們把它擴展到了(le)近似（approximate）因子模型，即允許擾動有弱相關性，因此 $\Sigma_u$ 不再是對(duì)角陣。De Nard, Ledoit, and Wolf (2021) 的(de)研究發現，在近似因子模型假設下(xià)，對(duì) $\Sigma_u$ 進行非線性收縮，從而得(de)到的(de)協方差矩陣的(de)估計量結果更優。

另外值得(de)一提的(de)是，對(duì)于使用(yòng)多(duō)因子模型估計協方差矩陣而言，使用(yòng)哪些因子以及不同因子會對(duì)估計結果産生怎樣的(de)影(yǐng)響注定是繞不過去的(de)坎。然而真實定價模型裏有哪些因子是未知的(de)，因此我們大(dà)概率會使用(yòng)一個(gè)設誤的(de)版本。De Nard, Ledoit, and Wolf (2021) 指出，在近似因子模型假設下(xià)對(duì) $\Sigma_u$ 估計時(shí)，他(tā)們的(de)算(suàn)法能從殘差中識别出因模型設誤造成的(de)殘餘因子結構，因此依然能夠給出準确的(de)估計。這(zhè)從一定程度上削弱了(le)無法合理(lǐ)準确指定多(duō)因子模型所造成的(de)影(yǐng)響。

面對(duì)形形色色的(de)收縮估計量，小夥伴不禁會問，到底選擇哪一個(gè)。在實際使用(yòng)中，一個(gè)有效的(de)經驗法則是根據 $N$ 和(hé) $T$ 的(de)取值來(lái)選取适當的(de)方法。例如，Ledoit 和(hé) Wolf 指出，當 $N$ 很小時(shí)，收縮的(de)作用(yòng)并不明(míng)顯；又比如當 $N$ 和(hé) $T$ 均大(dà)于 50 時(shí)，非線性收縮将會比線性收縮更具優勢。

除此之外，在比較協方差矩陣估計量時(shí)，一個(gè)常用(yòng)的(de)方法是構造最小方差（minimum variance）投資組合，并考察每個(gè)估計量構造的(de)組合在樣本外實際方差的(de)大(dà)小（Ledoit and Wolf 2017）。由于最小方差投資組合僅僅利用(yòng)協方差矩陣作爲輸入，因此它不會受到預期收益率估計誤差的(de)影(yǐng)響。

本文簡要且有側重地回顧了(le) Ledoit 和(hé) Wolf 兩位在協方差估計方面多(duō)年的(de)嘗試。他(tā)們的(de)方法從線性收縮到非線性收縮，從靜态到動态模型，不僅提高(gāo)了(le)協方差矩陣估計的(de)準确性，也(yě)極大(dà)地擴展了(le)其應用(yòng)的(de)範圍。沿著(zhe)他(tā)們二位已經鋪好的(de)道路，我們能在估計協方差矩陣的(de)道路上走得(de)更遠(yuǎn)。

參考文獻

De Nard, G., O. Ledoit, and M. Wolf (2021). Factor models for portfolio selection in large dimensions: The good, the better and the ugly. Journal of Financial Econometrics 19(2), 236-257.

James, W. and C. Stein (1961). Estimation with quadratic loss. Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, vol. 1. Oakland, CA, USA: University of California Press, pp. 361-380.

Ledoit, O. and M. Wolf (2003). Improved estimation of the covariance matrix of stock returns with an application to portfolio selection. Journal of Empirical Finance 10(5), 603-621.

Ledoit, O. and M. Wolf. (2004b). A well-conditioned estimator for large-dimensional covariance matrices. Journal of Multivariate Analysis 88(2), 365-411.

Ledoit, O. and M. Wolf (2015). Spectrum estimation: A unified framework for covariance matrix estimation and PCA in large dimensions. Journal of Multivariate Analysis 139, 360-384.

Ledoit, O. and M. Wolf (2017). Nonlinear shrinkage of the covariance matrix for portfolio selection: Markowitz meets Goldilocks. Review of Financial Studies 30(12), 4349-4388.

Ledoit, O. and M. Wolf (2020). Analytical nonlinear shrinkage of large-dimensional covariance matrices. Annals of Statistics 48(5), 3043-3065.

Ledoit, O. and M. Wolf (2022). The power of (non-)linear shrinkage: A review and guide to covariance matrix estimation. Journal of Financial Econometrics 20(1), 187-218.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。

合格投資者聲明(míng)

Ledoit and Wolf 的(de)協方差矩陣收縮之旅