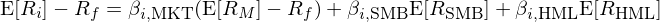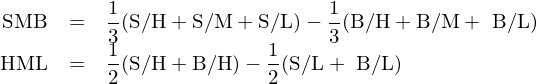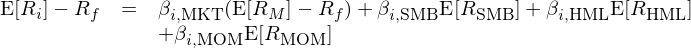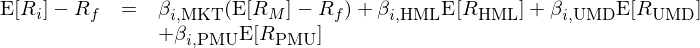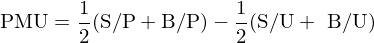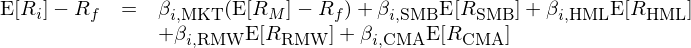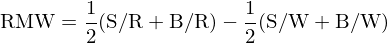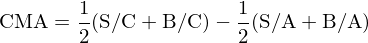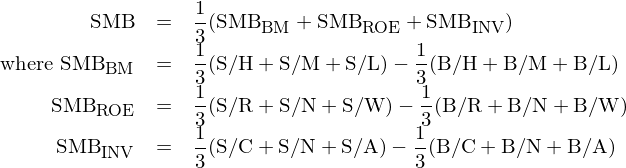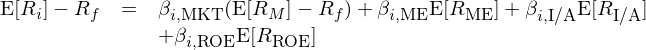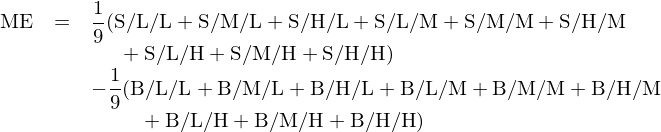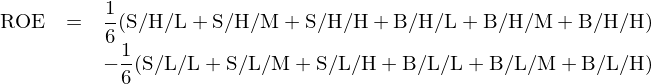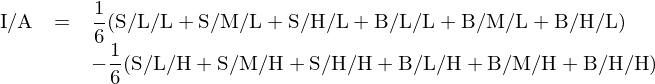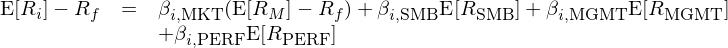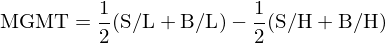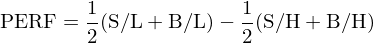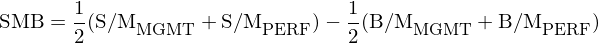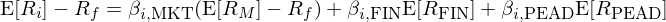主流多(duō)因子模型巡禮
發布時(shí)間:2020-09-01 | 來(lái)源: 川總寫量化(huà)
特别說明(míng):本文節選自石川、劉洋溢、連祥斌所著《因子投資:方法與實踐》,有删改。
0 引言
在過去相當長(cháng)的(de)一段時(shí)間内,公衆号陸續介紹了(le)很多(duō)因子投資的(de)内容,目的(de)是爲小夥伴們搭建因子投資的(de)知識體系。這(zhè)些内容涵蓋了(le)因子、異象以及資産定價的(de)方方面面,且很多(duō)都是最前沿的(de)研究。不過,仔細回顧之後,我發現公衆号尚未對(duì)主流的(de)多(duō)因子模型進行梳理(lǐ)。究其原因,可(kě)能是我感覺大(dà)家對(duì) Fama-French 三因子模型或 q-factor 模型這(zhè)些都太熟悉了(le);也(yě)可(kě)能是因爲随著(zhe)人(rén)們對(duì)資産定價理(lǐ)解的(de)越來(lái)越深入,在截面模型面前,這(zhè)些基于時(shí)序回歸的(de)模型已風光(guāng)不再。然而,無論是爲了(le)完善知識體系,還(hái)是爲了(le)了(le)解資産定價研究發展的(de)曆史進程,通(tōng)過一篇文章(zhāng)來(lái)梳理(lǐ)學術界提出的(de)主流多(duō)因子模型仍然顯得(de)十分(fēn)必要,因此就有了(le)本文。在我看來(lái),本文是因子投資知識體系中必不可(kě)少的(de)一塊 building block;也(yě)希望它能成爲各位小夥伴因子投資工具箱中一篇順手的(de)參考文獻。
自 Fama and French (1993) 發表并提出第一個(gè)多(duō)因子模型以來(lái),學術界對(duì)多(duō)因子模型的(de)研究經曆了(le)近 30 年。其間,很多(duō)新的(de)模型先後被提出,它們對(duì)人(rén)們認知市場(chǎng)産生了(le)深遠(yuǎn)的(de)影(yǐng)響。下(xià)表總結了(le)當下(xià)學術界主流的(de)多(duō)因子模型,其中最“年長(cháng)”的(de) Fama-French 三因子模型已經“高(gāo)齡”27 歲,而最“年輕”的(de) Daniel-Hirshleifer-Sun 三因子模型卻還(hái)是個(gè)“小嬰兒(ér)”。
有必要說明(míng)的(de)是,本文并沒有考慮 Barillas and Shanken (2018) 通(tōng)過統計學手段的(de)檢驗而“攢”出來(lái)的(de)六因子模型,也(yě)并沒有将 Hou et al. (2020) 在 Hou, Xue, and Zhang (2015) 基礎上提出的(de) q5 模型納入。雖說新模型的(de)提出是爲了(le)取代老模型,但目前學術界就各個(gè)模型的(de)孰優孰劣尚未達成一緻。正如 Fama-French 三、五因子模型如今依然是實證資産定價研究中被使用(yòng)最廣泛的(de)定價模型,而像 Hou-Xue-Zhang 四因子模型和(hé) Daniel-Hirshleifer-Sun 三因子模型這(zhè)些完全從不同角度推出的(de)模型也(yě)極大(dà)地豐富了(le)人(rén)們對(duì)資産定價及因子投資的(de)理(lǐ)解。下(xià)文就将對(duì)上述 7 個(gè)模型逐一說明(míng)。
1 Fama-French 三因子模型
Fama and French (1993) 三因子模型是基于 Fama and French (1992) 水(shuǐ)到渠成的(de)結果。自上世紀 70 年代以來(lái),CAPM 開始遭到各種質疑,而 Fama and French (1992) 将各種 CAPM 無法解釋的(de)異象進行了(le)整合,徹底颠覆了(le)人(rén)們對(duì) CAPM 的(de)看法。當然,CAPM 數學上足夠簡單優雅,且在業務上非常容易解釋,因此它還(hái)是資産定價的(de)一個(gè)很好的(de)出發點,隻是人(rén)們再也(yě)無法忽視不能夠被 CAPM 解釋的(de)其他(tā)系統性風險因子。
爲了(le)摒棄一個(gè)舊(jiù)模型,唯有提出一個(gè)新模型。Fama and French (1993) 在 CAPM 的(de)基礎上加入了(le)價值(High-Minus-Low,即 HML)和(hé)規模(Small-Minus-Big,即 SMB)兩因子,提出了(le) Fama-French 三因子模型,它也(yě)是多(duō)因子模型的(de)開山鼻祖:
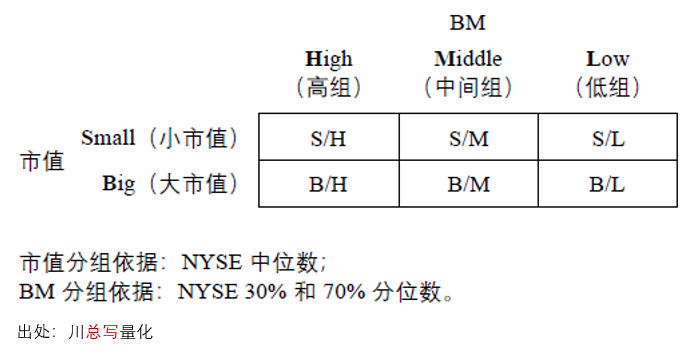
式中 E[R_i] 表示股票(piào) i 的(de)預期收益率,R_f 爲無風險收益率,E[R_M] 爲市場(chǎng)組合預期收益率,E[R_SMB] 和(hé) E[R_HML] 分(fēn)别爲規模因子(SMB)以及價值因子(HML)的(de)預期收益率,β_MKT、β_SMB 和(hé) β_HML 爲個(gè)股 i 在相應因子上的(de)暴露。爲構建價值和(hé)規模因子,Fama and French (1993) 使用(yòng) book-to-market ratio(BM)和(hé)市值進行了(le)下(xià)圖所示的(de) 2 × 3 獨立雙重排序。在排序時(shí),他(tā)們以紐約證券交易所(NYSE)中上市公司的(de)市值中位數爲界,把 NYSE、納斯達克(NASDAQ)以及美(měi)國證券交易所(AMEX)的(de)上市公司分(fēn)成小市值(Small)和(hé)大(dà)市值(Big)兩組。類似的(de),以 NYSE 中上市公司 BM 的(de) 30% 和(hé) 70% 分(fēn)位數爲界,把這(zhè)三大(dà)交易所的(de)上市公司分(fēn)成三組:BM 高(gāo)于 70% 分(fēn)位數的(de)爲 High 組、BM 低于 30% 分(fēn)位數的(de)爲 Low 組、位于中間的(de)爲 Middle 組。
通(tōng)過以上劃分(fēn)後得(de)到 6 個(gè)組,分(fēn)别記爲 S/H、S/M、S/L、B/H、B/M 以及 B/L。将每組中的(de)股票(piào)收益率按市值加權得(de)到 6 個(gè)投資組合;利用(yòng)它們,Fama and French (1993) 使用(yòng)如下(xià)方法構造 HML 和(hé) SMB 兩因子:
在每年六月(yuè)末,使用(yòng)上一财年最新的(de)财務數據對(duì)股票(piào)重新排序并對(duì)這(zhè)兩個(gè)因子進行再平衡。Fama-French 三因子模型被提出後逐步便取代了(le) CAPM 成爲資産定價的(de)第一範式。而上述雙重排序以及以此衍生出來(lái)的(de)多(duō)重劃分(fēn)來(lái)構建因子組合也(yě)成爲學術界競相模仿的(de)對(duì)象。
2 Carhart 四因子模型
Fama-French 三因子模型雖然有足夠的(de)開創性,但是“适用(yòng)性”卻有限,有很多(duō)其無法解釋的(de)異象。在衆多(duō)異象中,最顯著的(de)當屬截面動量異象。該異象最初由 Jegadeesh and Titman (1993) 提出,但卻被 Eugene Fama 自己的(de)學生 Carhart 發揚光(guāng)大(dà)。說句題外話(huà):Eugene Fama 從來(lái)不否認動量的(de)存在,正如他(tā)從來(lái)不承認動量作爲一個(gè)正式的(de)因子。無獨有偶,Fama 的(de)另一個(gè)弟(dì)子 Cliff Asness 博士論文研究的(de)也(yě)是動量。Asness 曾提到他(tā)和(hé) Fama 說他(tā)希望研究動量,Fama 泰然的(de)回應道 “如果它在那,就去寫吧”。
回到 Jegadeesh and Titman (1993)。假如當前爲 t 月(yuè),該文使用(yòng) t - 12 到 t - 1 這(zhè) 11 個(gè)月(yuè)之間的(de)總收益率将所有股票(piào)排序,并選擇總收益率高(gāo)的(de)構建了(le)赢家組合(Winner)、總收益率低的(de)構建了(le)輸家組合(Loser),并發現做(zuò)多(duō)赢家做(zuò)空輸家獲得(de)的(de)多(duō)/空投資組合可(kě)以獲得(de)超額收益。之所以特意規避到最近的(de)一個(gè)月(yuè)是爲了(le)規避市場(chǎng)短期存在反轉現象。受到 Jegadeesh and Titman (1993) 的(de)啓發,Carhart (1997) 在 Fama-French 三因子模型中加入了(le)截面動量因子(取動量英文單詞前三個(gè)字母、記爲 MOM)并提出了(le) Carhart 四因子模型:
上式中 E[R_MOM] 爲動量因子的(de)收益率,β_MOM 爲個(gè)股 i 在動量因子上的(de)暴露。在實際使用(yòng)中,Carhart (1997) 使用(yòng) NYSE、NASDAQ 以及 AMEX 的(de)全部股票(piào),每月(yuè)末将它們按 t - 12 到 t - 1 這(zhè) 11 個(gè)月(yuè)的(de)總收益率排序,并通(tōng)過做(zuò)多(duō)排名前 30% 同時(shí)做(zuò)空排名後 30% 的(de)股票(piào)構建動量因子。值得(de)一提的(de)是,Carhart 并未使用(yòng)動量和(hé)市值進行雙重排序,且在計算(suàn)動量因子收益率時(shí),多(duō)空兩頭内的(de)股票(piào)均采用(yòng)等權配置。
3 Novy-Marx 四因子模型
2013 年,Novy-Marx 職業生涯 so far 的(de)代表作 Novy-Marx (2013) 橫空出世。而伴随該文提出的(de)盈利因子,一個(gè)四因子模型也(yě)浮出了(le)水(shuǐ)面:
其中 E[R_PMU] 是盈利因子的(de)預期收益率(PMU 是 Profitability-Minus-Unprofitability 的(de)縮寫,代表盈利),β_PMU 爲個(gè)股 i 在該因子上的(de)暴露。除盈利因子外,該模型還(hái)包括市場(chǎng)、價值(HML)以及動量(UMD)因子。有意思的(de)是,Novy-Marx 使用(yòng) UMD(Up-Minus-Down 的(de)首字母縮寫)代表動量因子,因此上式中 E[R_UMD] 和(hé) β_UMD 分(fēn)别爲動量因子的(de)預期收益以及個(gè)股 i 在該因子上的(de)暴露。在使用(yòng)時(shí),動量因子的(de)投資組合每月(yuè)進行再平衡,而價值和(hé)盈利因子每年六月(yuè)末使用(yòng)最新的(de)财務數據重新構建投資組合。
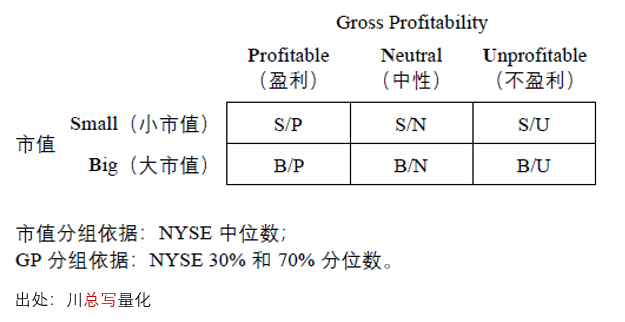
如何衡量企業的(de)盈利能力呢(ne)?Novy-Marx (2013) 出于各種原因,認爲毛利潤(Gross Profitability,簡稱 GP)要比淨利潤更好。不過在兩年後,他(tā)就被另一個(gè)位大(dà)佬 Ray Ball 回擊了(le)(Ball et al. 2015),具體見《建設性怼人(rén)》。抛開争議(yì),在構建盈利因子時(shí),Novy-Marx (2013) 追随了(le) Fama and French (1993) 的(de)腳步,分(fēn)别使用(yòng)相應的(de)指标與市值進行雙重排序法。由此可(kě)知,該模型中的(de)動量因子和(hé) Carhart 四因子模型中的(de)動量因子不同,因爲後者的(de)動量因子是通(tōng)過單變量排序構造。下(xià)面重點介紹一下(xià)盈利因子(PMU)的(de)構建(下(xià)圖)。
以 NYSE 中上市公司的(de) GP 的(de) 30% 和(hé) 70% 分(fēn)位數爲界,把 NYSE、NASDAQ 以及 AMEX 三大(dà)所上市公司依據 GP 高(gāo)低分(fēn)爲盈利(Profitability,即 GP 在 70% 分(fēn)位數之上)、中性(Neutral,即 GP 介于 30% 和(hé) 70% 分(fēn)位數之間)以及不盈利(Unprofitability,即 GP 在 30% 分(fēn)位數之下(xià))三組。這(zhè)三組和(hé)市值高(gāo)低一起劃分(fēn)共得(de)到 6 個(gè)投資組合:S/P、S/N、S/U、B/P、B/N 以及 B/U。每個(gè)組合中的(de)股票(piào)均按其市值确定權重。
與 Fama-French 三因子以及 Carhart 四因子模型不同的(de)是,Novy-Marx (2013) 在構建因子時(shí)進行了(le)行業中性處理(lǐ),即在做(zuò)多(duō)一支股票(piào)的(de)同時(shí)按同等權重做(zuò)空該股票(piào)所屬的(de)行業指數,從而得(de)到行業中性化(huà)後的(de)投資組合。最後,由于盈利和(hé)預期收益率正相關,因此使用(yòng)盈利組 S/P 和(hé) B/P 和(hé)不盈利組 S/U 和(hé) B/U 的(de)收益率之差構建盈利因子:
4 Fama-French 五因子模型
接下(xià)來(lái)看看頗受争議(yì)的(de) Fama-French 五因子模型。原因嘛,公衆号的(de)老朋友想必不再陌生了(le)。需要背景知識的(de)小夥伴請看《q-factor 往事》以及《從 Factor Zoo 到 Factor War,實證資産定價走向何方》。2015 年,Eugene Fama 和(hé)老搭檔 Ken French 在他(tā)們的(de)三因子模型基礎上添加了(le)盈利和(hé)投資兩個(gè)因子,提出了(le)新的(de)五因子模型:
式中 E[R_RMW] 和(hé) E[R_CMA] 分(fēn)别爲盈利和(hé)投資因子的(de)預期收益率,β_RMW 和(hé) β_CMA 分(fēn)别爲個(gè)股 i 在這(zhè)兩個(gè)因子上的(de)暴露。每年六月(yuè)末,使用(yòng)最新财務數據對(duì)股票(piào)重新排序并對(duì)規模、價值、盈利和(hé)投資這(zhè)四個(gè)因子投資組合進行再平衡。從某種程度上說,Fama-French 五因子模型是他(tā)們向學界各種異象妥協的(de)結果。随著(zhe)諸多(duō)無法被三因子模型解釋的(de)異象相繼被提出,他(tā)們意識到了(le)在定價模型中加入新因子的(de)必要性。五因子模型正是這(zhè)個(gè)背景下(xià)的(de)産物(wù),而它也(yě)自然而然的(de)接過了(le)三因子模型的(de)槍,成爲實證資産定價中的(de)第一 benchmark(至少在很長(cháng)時(shí)間内)。
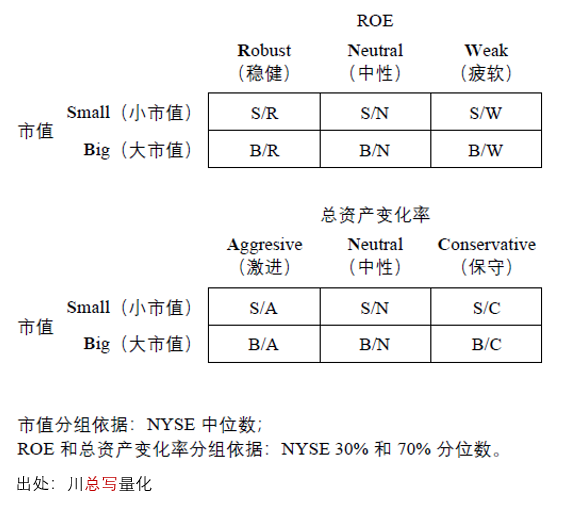
該五因子模型背後的(de)動機是股息貼現模型(Dividend Discount Model,簡稱 DDM),而構建因子的(de)變量則可(kě)以追溯到 Fama and French (2006) 這(zhè)篇研究盈利和(hé)投資的(de)文章(zhāng)。該模型的(de)金融學含義已經在《從 Factor Zoo 到 Factor War,實證資産定價走向何方》做(zuò)過介紹,本文不再贅述。在構建因子時(shí),對(duì)于新加入的(de)盈利和(hé)投資因子,依次使用(yòng) ROE 以及過去一年總資産變化(huà)率和(hé)市值進行 2 × 3 雙重排序,分(fēn)别得(de)到六個(gè)投資組合(下(xià)圖)。
首先以 NYSE 中上市公司的(de) ROE 的(de) 30% 和(hé) 70% 分(fēn)位數爲界,把 NYSE、NASDAQ 以及 AMEX 三大(dà)所上市公司依據 ROE 高(gāo)低分(fēn)爲穩健(Robust,即 ROE 在 70% 分(fēn)位數之上)、中性(Neutral,即 ROE 介于 30% 和(hé) 70% 分(fēn)位數之間)以及疲軟(Weak,即 ROE 在 30% 分(fēn)位數之下(xià))三組。這(zhè)三組和(hé)市值高(gāo)低獨立排序共得(de)到 6 個(gè)投資組合:S/R、S/N、S/W、B/R、B/N 以及 B/W,每個(gè)投資組合的(de)收益率使用(yòng)各組成分(fēn)股收益率的(de)市值加權得(de)到。對(duì)于盈利因子,由于預期盈利和(hé)預期收益率正相關,因此使用(yòng)穩健組 S/R 和(hé) B/R 和(hé)疲軟組 S/W 和(hé) B/W 的(de)收益率之差構建盈利因子(Robust-Minus-Weak,簡稱 RMW):
類似的(de),對(duì)于投資因子,以 NYSE 中上市公司總資産變化(huà)率的(de) 30% 和(hé) 70% 分(fēn)位數爲界,把三大(dà)所上市公司依據總資産變化(huà)率高(gāo)低分(fēn)爲 激進(Aggressive,即總資産變化(huà)率在 70% 分(fēn)位數之上)、中性(Neutral,即總資産變化(huà)率介于 30% 和(hé) 70% 分(fēn)位數之間)以及保守(Conservative,即總資産變化(huà)率在 30% 分(fēn)位數之下(xià))三組。用(yòng)這(zhè)三組和(hé)市值高(gāo)低進行雙重排序就得(de)到 6 個(gè)投資組合:S/A、S/N、S/C、B/A、B/N 以及 B/C。由于預期投資和(hé)預期收益率負相關,因此使用(yòng)保守組 S/C 和(hé) B/C 和(hé)激進組 S/A 和(hé) B/A 的(de)收益率之差構建投資因子(Conservative-Minus-Aggressive,簡稱 CMA):
最後值得(de)一提的(de)是規模因子(SMB)的(de)構建方法。與 Fama-French 三因子模型不同,在五因子模型中,BM、ROE 以及總資産變化(huà)率分(fēn)别用(yòng)來(lái)和(hé)市值進行雙重排序,一共得(de)到了(le) 18 個(gè)投資組合。在這(zhè)種情況下(xià),如果還(hái)像三因子模型一樣,僅使用(yòng) BM 和(hé)市值的(de)分(fēn)組來(lái)構建規模因子就難言合理(lǐ) —— 人(rén)們一定會質疑爲什(shén)麽不用(yòng)市值和(hé) ROE 或總資産變化(huà)率的(de)分(fēn)組組合。顯然,Fama and French (2015) 考慮到了(le)這(zhè)個(gè)問題,因此他(tā)們選擇綜合上述三個(gè)變量各自和(hé)市值雙重排序得(de)到的(de)小市值和(hé)大(dà)市值組合來(lái)構建規模因子。最終,規模因子(SMB)爲:
5 Hou-Xue-Zhang 四因子模型
說完了(le) Fama-French 五因子,就不能不提把它當靶子打的(de) q-factor model(Hou, Xue, and Zhang 2015),也(yě)被稱爲 Hou-Xue-Zhang 四因子模型。(背景知識依然見《q-factor 往事》以及《從 Factor Zoo 到 Factor War,實證資産定價走向何方》。)Hou, Xue, and Zhang (2015) 從實體投資經濟學理(lǐ)論出發提出了(le)一個(gè)四因子模型。由于實體投資經濟學理(lǐ)論又被稱爲 q-theory,因此該模型也(yě)被學術界稱爲 q-factor model。該模型包含市場(chǎng)、規模、投資和(hé)盈利四因子:
式中 E[R_ME]、E[R_I/A] 和(hé) E[R_ROE] 分(fēn)别爲規模、投資和(hé)盈利因子的(de)預期收益,β_ME、β_I/A 和(hé) β_ROE 爲股票(piào) i 在相應因子上的(de)暴露。在使用(yòng)中需要明(míng)确的(de)是,規模和(hé)投資因子的(de)排序變量每年六月(yuè)末更新,而盈利因子的(de)排序變量每月(yuè)末更新;但所有因子的(de)投資組合均是月(yuè)度再平衡。
Hou-Xue-Zhang 四因子模型是受到 Cochrane (1991) 啓發,源于公司投資的(de)經濟學原理(lǐ)。該論文的(de)作者之一張橹教授曾在清華金融評論上撰文介紹過這(zhè)個(gè)模型的(de)來(lái)龍去脈,對(duì)其的(de)具體解釋請參考《從 Factor Zoo 到 Factor War,實證資産定價走向何方》,本文不再贅述。在實證研究中,Hou, Xue, and Zhang (2015) 使用(yòng) ROE 和(hé)總資産變化(huà)率作爲代表盈利和(hé)投資的(de)指标。在構建因子時(shí),爲了(le)體現上述條件預期收益率的(de)關系,他(tā)們使用(yòng)市值、單季度 ROE 和(hé)總資産變化(huà)率進行 2 × 3 × 3 獨立三重排序,其中市值按紐交所中位數劃分(fēn)、ROE 和(hé)總資産變化(huà)率按紐交所 30% 和(hé) 70% 分(fēn)位數進行劃分(fēn)。
獨立三重排序共得(de)到 18 個(gè)投資組合,每個(gè)組合内的(de)股票(piào)按照(zhào)市值加權。令 c_1、c_2、c_3 依次代表每個(gè)投資組合在市值、ROE 和(hé)總資産變化(huà)率三個(gè)變量上的(de)劃分(fēn),其中 c_1 取值爲 S 或 B 代表小、大(dà)市值,c_2 和(hé) c_3 取值爲 H、M、L 代表高(gāo)、中、低三檔;令數學符号 c_1/c_2/c_3 代表上述三個(gè)變量某個(gè)劃分(fēn)交集得(de)到的(de)分(fēn)組。例如 S/H/H 代表由小市值、高(gāo) ROE 和(hé)高(gāo)總資産變化(huà)率股票(piào)構成的(de)分(fēn)組。依照(zhào)上述數學符号,使用(yòng)這(zhè) 18 個(gè)投資組合,規模(記爲 ME)、盈利(記爲 ROE)、投資(記爲 I/A)三因子的(de)定義如下(xià):
由上述公式可(kě)知,規模因子(ME)是等權做(zuò)多(duō) 9 個(gè)小市值組合(S/c_2/c_3)、同時(shí)等權做(zuò)空 9 個(gè)大(dà)市值組合(B/c_2/c_3);盈利因子(ROE)是等權做(zuò)多(duō) 6 個(gè)高(gāo) ROE 組合(c_1/H/c_3),同時(shí)等權做(zuò)空 6 個(gè)低 ROE 組合(c_1/L/c_3);投資因子(I/A)是等權做(zuò)多(duō) 6 個(gè)低總資産變化(huà)率組合(c_1/c_2/L),同時(shí)等權做(zuò)空 6 個(gè)高(gāo)總資産變化(huà)率組合(c_1/c_2/H)。以上介紹的(de) 4 個(gè)多(duō)因子模型都還(hái)是從傳統的(de)經濟學和(hé)金融學理(lǐ)論出發的(de);而接下(xià)來(lái)的(de)兩個(gè)則打破了(le)這(zhè)個(gè)慣例,均屬于從行爲金融學角度對(duì)資産定價進行的(de)探索。
6 Stambaugh-Yuan 四因子模型
Stambaugh and Yuan (2017) 在市場(chǎng)和(hé)規模因子的(de)基礎上,引入管理(lǐ)因子和(hé)表現因子,構建了(le)四因子模型:
式中 E[R_MGMT] 和(hé) E[R_PERF] 分(fēn)别爲管理(lǐ)和(hé)表現因子的(de)預期收益率;β_MGMT 和(hé) β_PERF 爲個(gè)股 i 在相應因子上的(de)暴露。在使用(yòng)中,規模、管理(lǐ)和(hé)表現三個(gè)因子投資組合的(de)再平衡頻(pín)率均爲月(yuè)頻(pín)。在上述四因子模型中,管理(lǐ)因子和(hé)表現因子均源自關于錯誤定價的(de)研究。錯誤定價意味著(zhe)價格較内在價值的(de)偏離,當價格高(gāo)于内在價值時(shí)資産被高(gāo)估,當價格低于内在價值時(shí)資産被低估。被高(gāo)估的(de)資産在未來(lái)由于價格的(de)修正會出現較低的(de)收益率,反之被低估的(de)資産在未來(lái)則會獲得(de)更高(gāo)的(de)收益率。爲了(le)從錯誤定價中尋找因子的(de)靈感,首先要找到衡量股票(piào)價格是否被高(gāo)估或低估的(de)指标。
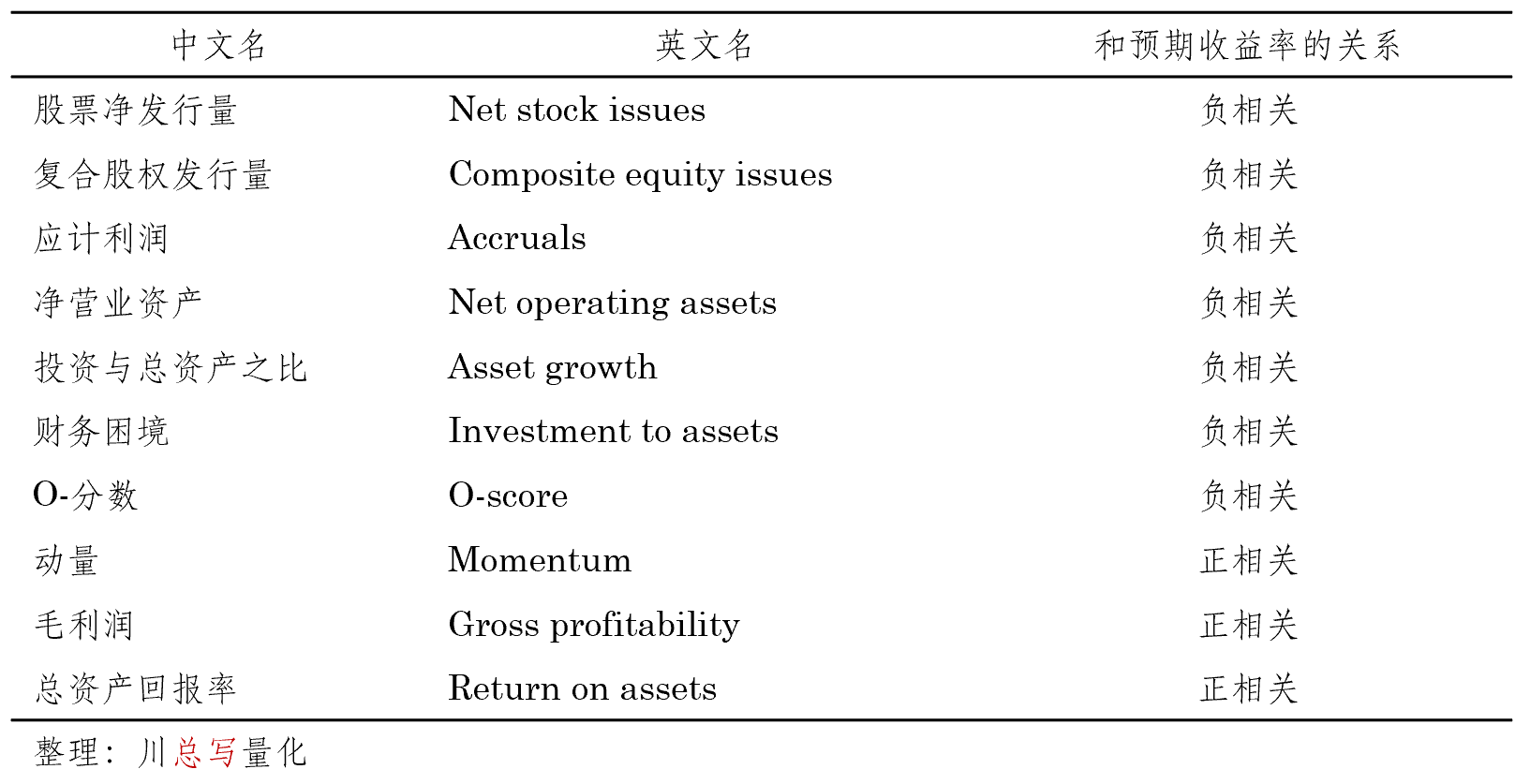
爲此,Stambaugh and Yuan (2017) 延續了(le)兩位作者以及他(tā)們的(de)另外一位合作者餘劍峰教授在早期關于錯誤定價的(de)一系列研究,以 11 個(gè) Fama-French 三因子模型無法解釋的(de)異象爲基礎,構建了(le)錯誤定價指标。這(zhè)麽做(zuò)背後的(de)邏輯是,異象的(de)超額收益反映了(le)其投資組合内股票(piào)的(de)收益中無法被 Fama-French 三因子模型解釋的(de)超額收益,即個(gè)股的(de)錯誤定價。因此,異象變量取值的(de)高(gāo)低就可(kě)以用(yòng)來(lái)描述錯誤定價的(de)方向(被高(gāo)估或是低估)和(hé)大(dà)小。這(zhè) 11 個(gè)異象包括:
将這(zhè) 11 個(gè)異象根據它們之間的(de)相關性分(fēn)成兩組,使得(de)每組内的(de)異象之間相關性更高(gāo),而分(fēn)屬兩組的(de)異象相關性較低。第一組包含股票(piào)淨發行量、複合股權發行量、應計利潤、淨營業資産、總資産增長(cháng)率以及投資與總資産之比 6 個(gè)異象。這(zhè) 6 個(gè)異象變量均和(hé)上市公司的(de)管理(lǐ)決策相關,使用(yòng)它們構建的(de)因子被稱爲管理(lǐ)因子。第二組包含另外 5 個(gè)異象,即财務困境、O-分(fēn)數、動量、毛利率以及總資産回報率。它們均和(hé)上市公司的(de)表現有關,使用(yòng)它們構建的(de)因子被稱爲表現因子。
在每月(yuè)末,對(duì)于這(zhè)兩組中的(de)每一個(gè)異象,使用(yòng)異象變量在截面上對(duì)股票(piào)排序。排序時(shí),從每個(gè)異象指标和(hé)未來(lái)預期收益率的(de)相關性方向(即正、負相關)出發,将被高(gāo)估的(de)股票(piào)排在前面、被低估的(de)股票(piào)排在後面。如果異象變量和(hé)收益率呈負相關(比如應計利潤),則按變量取值從大(dà)到小排序,取值最高(gāo)的(de)排第一、第二高(gāo)的(de)排第二、以此類推、取值最小的(de)排最後。反之,如果異象變量和(hé)收益率呈正相關(比如動量),則按變量取值從小到大(dà)排序,取值最低的(de)排第一、第二低的(de)排第二、以此類推、取值最高(gāo)的(de)排最後。使用(yòng)全部異象變量對(duì)股票(piào)排序後,每支股票(piào)就有 11 個(gè)分(fēn)數。把管理(lǐ)和(hé)表現兩組内的(de) 6 個(gè)和(hé) 5 個(gè)異象排名取平均,就得(de)到每支股票(piào)在兩組内各自的(de)綜合排名。綜合排名越高(gāo),說明(míng)該股票(piào)價格越被高(gāo)估,其未來(lái)預期收益越低;綜合排名越低,說明(míng)該股票(piào)價格越被低估,其未來(lái)預期收益越高(gāo)。
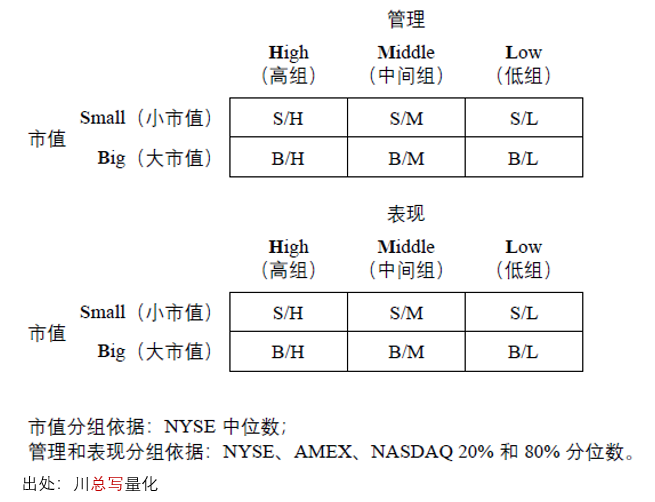
有了(le)股票(piào)在管理(lǐ)和(hé)表現這(zhè)兩個(gè)變量上的(de)排名,接下(xià)來(lái)使用(yòng)市值和(hé)這(zhè)兩個(gè)變量依次進行 2 × 3 雙重排序,構建管理(lǐ)、表現以及市值三個(gè)因子。有意思的(de)是,Stambaugh and Yuan (2017) 的(de)做(zuò)法和(hé)學術界的(de)傳統做(zuò)法又有不少差異。在使用(yòng)市值排序時(shí),該模型和(hé)其他(tā)多(duō)因子模型一緻,使用(yòng) NYSE 包含股票(piào)的(de)市值中位數将所有股票(piào)分(fēn)爲大(dà)、小市值兩組。然而,對(duì)于管理(lǐ)和(hé)表現這(zhè)兩個(gè)變量則是将三大(dà)交易所的(de)股票(piào)混合在一起,使用(yòng)所有股票(piào)在這(zhè)兩個(gè)變量上各自的(de) 20% 和(hé) 80% 分(fēn)位數劃分(fēn)成高(gāo)、中、低三組。這(zhè)種做(zuò)法和(hé)其他(tā)多(duō)因子模型的(de)處理(lǐ)有兩點不同:(1)劃分(fēn)的(de)斷點沒有使用(yòng) NYSE 股票(piào)的(de)分(fēn)位數,而是全部股票(piào)的(de)分(fēn)位數;(2)劃分(fēn)阈值沒采取傳統的(de) 30% 和(hé) 70% 分(fēn)位數而是另辟蹊徑采用(yòng)了(le) 20% 和(hé) 80% 的(de)分(fēn)位數。Stambaugh and Yuan (2017) 對(duì)上述處理(lǐ)并無太多(duō)解釋。然而,Hou et al. (2019) 卻對(duì)此提出了(le)質疑。該文複現了(le)上述方法并同時(shí)按照(zhào)傳統的(de) NYSE 30% 和(hé) 70% 分(fēn)位數的(de)方法構造了(le)管理(lǐ)和(hé)表現因子。結果發現,這(zhè)兩個(gè)錯誤定價因子對(duì)雙重排序的(de)構造方式十分(fēn)敏感。構建管理(lǐ)和(hé)表現兩因子的(de)雙重排序如下(xià)圖所示。
以管理(lǐ)因子爲例,雙重排序得(de)到 6 個(gè)投資組合,每個(gè)投資組合中的(de)股票(piào)均采用(yòng)市值加權配置。對(duì)于管理(lǐ)變量,由于低組表示被低估的(de)股票(piào)、高(gāo)組表示被高(gāo)估的(de)股票(piào),因此通(tōng)過做(zuò)多(duō)兩個(gè)低組、做(zuò)空兩個(gè)高(gāo)組就可(kě)以構建管理(lǐ)因子(MGMT)的(de)投資組合:
按照(zhào)同樣的(de)邏輯,使用(yòng)表現變量和(hé)市值的(de)雙重排序得(de)到的(de) 6 個(gè)投資組合(同樣的(de),投資組合采用(yòng)市值加權),構建表現因子(PERF)的(de)投資組合如下(xià):
最後來(lái)看 Stambaugh-Yuan 四因子模型中的(de)規模因子,它的(de)構建方法與傳統方法差異更大(dà)。上述分(fēn)别使用(yòng)管理(lǐ)和(hé)表現分(fēn)别與市值進行雙重排序,共得(de)到 12 個(gè)投資組合。爲構建規模因子,Stambaugh and Yuan (2017) 摒棄了(le)管理(lǐ)和(hé)表現兩變量的(de)高(gāo)、低組共 8 個(gè)組合,而僅使用(yòng)剩餘的(de) 4 個(gè)組合。換句話(huà)說,管理(lǐ)和(hé)表現分(fēn)别與市值雙重排序,得(de)到各自的(de) S/M 和(hé) B/M 組合。将兩個(gè) S/M 組合取平均并做(zuò)多(duō),将兩個(gè) B/M 組合取平均并做(zuò)空,以此構建規模因子(SMB)的(de)投資組合:
上式中,下(xià)标 MGMT 和(hé) PERF 分(fēn)别代表由管理(lǐ)和(hé)表現與市值雙重排序得(de)到的(de) S/M 或 B/M 投資組合。對(duì)于這(zhè)種構造方法,二位作者的(de)解釋是,傳統的(de)雙重排序方法會中性化(huà)錯誤定價對(duì)市值的(de)影(yǐng)響。然而,由于套利不對(duì)稱性(Stambaugh, Yu, and Yuan 2015),比如難以做(zuò)空,導緻價格被高(gāo)估的(de)股票(piào)的(de)錯誤定價難以被消除。此外,大(dà)量實證結果顯示,錯誤定價在小市值股票(piào)中更爲突出。這(zhè)些特點使得(de)傳統的(de)構造方法無法在規模因子的(de)多(duō)、空兩頭對(duì)稱地消除錯誤定價的(de)影(yǐng)響,造成規模因子有被高(gāo)估的(de)偏誤,因此不宜采用(yòng)。正因如此,Stambaugh and Yuan (2017) 才采用(yòng)了(le)不同的(de)方法構造規模因子。他(tā)們的(de)實證表明(míng),如此構造的(de)規模因子比傳統方法得(de)到的(de)規模因子有更高(gāo)的(de)風險溢價。
7 Daniel-Hirshleifer-Sun 三因子模型
Daniel, Hirshleifer, and Sun (2020) 提出的(de) Daniel-Hirshleifer-Sun 三因子模型是把行爲金融學應用(yòng)于資産定價的(de)另一個(gè)嘗試。該文從長(cháng)、短兩個(gè)時(shí)間尺度上提出兩個(gè)行爲因子(behavioral factors),與市場(chǎng)因子一起構成了(le)一個(gè)複合三因子模型:
式中 E[R_FIN] 和(hé) E[R_PEAD] 分(fēn)别代表長(cháng)周期和(hé)短周期的(de)兩個(gè)行爲因子的(de)預期收益;β_FIN 以及 β_PEAD 爲個(gè)股 i 在相應因子上的(de)暴露。在使用(yòng)中,FIN 因子的(de)投資組合每年六月(yuè)更新;PEAD 因子的(de)投資組合每月(yuè)更新。這(zhè)兩個(gè)行爲因子旨在捕捉由于過度自信(overconfidence)和(hé)有限注意力(limited attention)造成的(de)錯誤定價,從而解釋學術界之前發現的(de)大(dà)量選股異象。從行爲金融學的(de)角度出發,股票(piào)收益率之間的(de)共同運動通(tōng)常有兩個(gè)原因:(1)股票(piào)錯誤定價上的(de)共性;(2)投資者對(duì)于股票(piào)基本面新息的(de)錯誤反應上的(de)共性。
前者指出不同的(de)股票(piào)實際上暴露在一些共同的(de)風格風險上,而情緒沖擊會造成同一類風格的(de)股票(piào)收益率的(de)共同運動,因此同一類風格上的(de)股票(piào)存在相關性很高(gāo)的(de)錯誤定價。後者說明(míng)由于認知偏差,投資者難以對(duì)股票(piào)基本面方面的(de)新息做(zuò)出及時(shí)、正确的(de)反應,因此也(yě)會導緻錯誤定價。由于錯誤定價可(kě)以預測未來(lái)收益率,這(zhè)意味著(zhe)可(kě)以使用(yòng)行爲因子來(lái)構建一個(gè)多(duō)因子模型,以期更好的(de)解釋股票(piào)預期收益率之間的(de)截面差異。這(zhè)就是 Daniel, Hirshleifer, and Sun (2020) 的(de)研究動機。
此外,該文進一步指出市場(chǎng)上的(de)絕大(dà)多(duō)數異象可(kě)按照(zhào)時(shí)間尺度分(fēn)爲短和(hé)長(cháng)兩大(dà)類。短時(shí)間尺度的(de)異象大(dà)多(duō)來(lái)自投資者的(de)有限注意力,而長(cháng)時(shí)間尺度的(de)異象大(dà)多(duō)來(lái)自投資者的(de)過度自信。爲此三位作者提出了(le)捕捉長(cháng)尺度異象的(de) FIN 因子和(hé)捕捉短尺度異象的(de) PEAD 因子。關于 FIN 和(hé) PEAD 因子的(de)具體構造方法,請參考前文《一個(gè)加入行爲因子的(de)複合模型》。本文不再贅述。
8 結語
以上七節系統梳理(lǐ)了(le)學術界主流的(de)多(duō)因子模型。有必要強調的(de)是,在這(zhè)些多(duō)因子模型中,除了(le)市場(chǎng)因子外,所有的(de)風格因子的(de)構造方法都是首先通(tōng)過排序法得(de)到多(duō)個(gè)投資組合,繼而選擇其中一些做(zuò)多(duō)、另一些做(zuò)空的(de)方式。在這(zhè)個(gè)過程中,通(tōng)過排序法劃分(fēn)得(de)到的(de)每個(gè)投資組合内部的(de)股票(piào)均是按市值加權來(lái)配置的(de)。一旦有了(le)投資組合的(de)收益率之後,在計算(suàn)因子收益率時(shí),使用(yòng)的(de)則是這(zhè)些投資組合收益率的(de)簡單平均 —— 無論是多(duō)頭還(hái)是空頭,不同投資組合之間是等權配置。這(zhè)種處理(lǐ)方式正是學術界構建因子投資組合時(shí)的(de)慣例。唯一的(de)例外是 Carhart 四因子模型中的(de)動量因子,該因子采用(yòng)單變量排序、且多(duō)空兩個(gè)投資組合均采用(yòng)等權重構造。
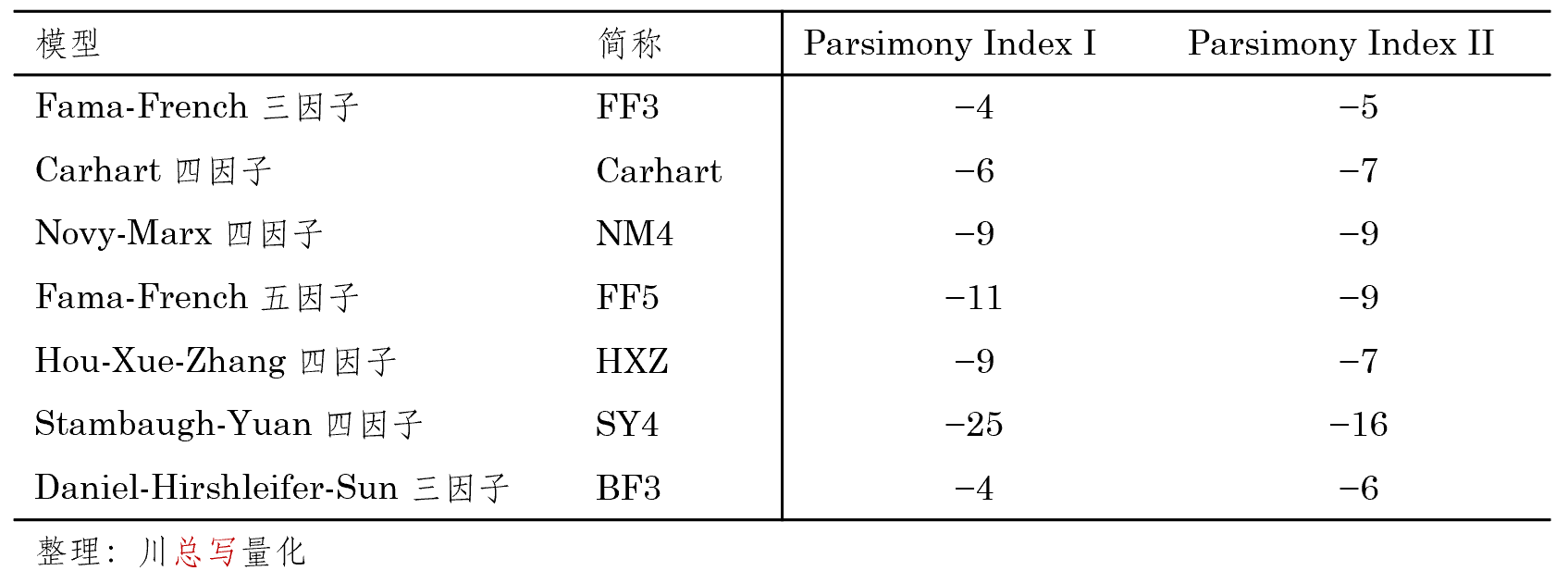
作爲本文的(de)結語,以下(xià)給出關于上述模型的(de)四點簡要討(tǎo)論。第一個(gè)討(tǎo)論是關于不同模型之間的(de) PK,即誰更能解釋股票(piào)的(de)預期收益。關于這(zhè)方面的(de)綜合 PK,感興趣的(de)小夥伴可(kě)以參考 Hou et al. (2019) 一文,該文對(duì)不同的(de)模型進行了(le)全方位無死角的(de)比較。結果嘛,你懂(dǒng)的(de)。第二個(gè)討(tǎo)論和(hé)上一條密切相關,即新提出的(de)模型往往比舊(jiù)模型有更多(duō)的(de)因子,或在構建因子時(shí)使用(yòng)了(le)更多(duō)的(de)指标(比如 Stambaugh-Yuan 四因子模型用(yòng)了(le) 11 個(gè)異象),因此它們優于老的(de)模型是意料之中的(de),否則也(yě)發表不出來(lái)。那麽問題來(lái)了(le):是否模型越複雜(zá)越好呢(ne)?利用(yòng) Daniel, Hirshleifer, and Sun (2020) 的(de)作者 Lin Sun 給出的(de)定義,計算(suàn)上述模型的(de)簡約指數,如下(xià)表所示,其中數值越低說明(míng)模型越複雜(zá)。從表中不難看到,新的(de)模型往往比舊(jiù)的(de)模型更加複雜(zá)。
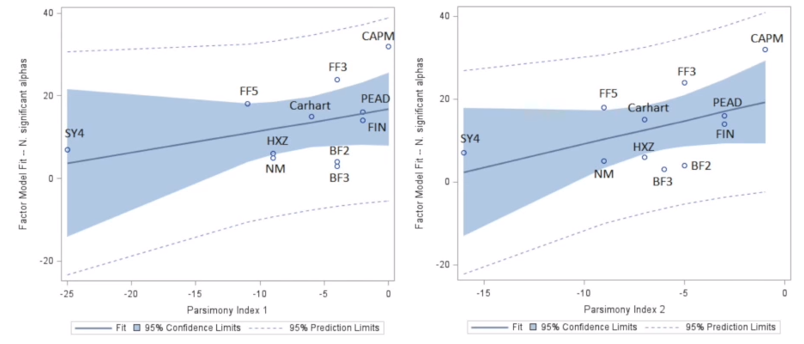
而顯然,越複雜(zá)的(de)模型越能解釋異象(下(xià)圖)。因此,在提出多(duō)因子模型時(shí),應該盡可(kě)能的(de)遵循簡約法則。在簡約法則的(de)指導思想下(xià),一個(gè)優秀的(de)因子模型通(tōng)常有較少的(de)因子或者基本面或量價特征;而作爲使用(yòng)者,我們應該盡量搞清楚每一個(gè)因子背後代表的(de)風險。
第三點思考是來(lái)自多(duō)因子模型背後的(de)含義。前文提到,最開始的(de)多(duō)因子模型背後的(de)動機均來(lái)自傳統金融學或經濟學原理(lǐ),而過去幾年中最新的(de)兩個(gè)模型卻都是來(lái)自行爲金融學,這(zhè)也(yě)許代表了(le)新的(de)研究風向。我猜學界有大(dà)佬對(duì)此可(kě)能很不高(gāo)興。不過不容否認的(de)是,行爲金融學确實受到了(le)越來(lái)越多(duō)的(de)關注和(hé)認可(kě)。比如,剛剛卸任的(de) AFA 主席正是行爲金融學大(dà)佬、Daniel, Hirshleifer, and Sun (2020) 作者之一的(de) David Hirshleifer。關于最後一點思考,讓我們來(lái)和(hé)文章(zhāng)開頭呼應下(xià)。本文介紹的(de) 7 個(gè)模型均是時(shí)序多(duō)因子模型(Fama and French 2020)。大(dà)量新鮮出爐、還(hái)冒著(zhe)熱(rè)氣的(de)研究成果表明(míng)通(tōng)過 portfolio sort 構建因子組合,通(tōng)過時(shí)序回歸計算(suàn)因子暴露并不能很好的(de)解釋股票(piào)的(de)預期收益率(見《A new norm?》、《Which beta?》、《Which beta II?》、《Which test assets?》)。
也(yě)許終有一天這(zhè)些模型将淡出人(rén)們的(de)視線。然而在那之前,它們依然是我們理(lǐ)解資産定價的(de)重要途徑;它們不應該被遺忘,因爲上述所有模型,都在曆史的(de)浪潮中見證了(le)金融學發展的(de)黃(huáng)金時(shí)代。
參考文獻
Ball, R., J. Gerakos, J. T. Linnainmaa, and V. V. Nikolaev (2015). Deflating profitability. Journal of Financial Economics 117(2), 225 – 248.
Barillas, F. and J. Shanken (2018). Comparing asset pricing models. Journal of Finance 73(2), 715 – 754.
Carhart, M. M. (1997). On persistence in mutual fund performance. Journal of Finance 52(1), 57 – 82.
Cochrane, J. H. (1991). Production-based asset pricing and the link between stock returns and economic fluctuations. Journal of Finance 46(1), 209 – 237.
Daniel, K. D., D. A. Hirshleifer, and L. Sun (2020). Short- and long-horizon behavioral factors. Review of Financial Studies 33(4), 1673 – 1736.
Fama, E. F. and K. R. French (1992). The cross-section of expected stock returns. Journal of Finance 47(2), 427 – 465.
Fama, E. F. and K. R. French (1993). Common risk factors in the returns on stocks and bonds. Journal of Financial Economics 33(1), 3 – 56.
Fama, E. F. and K. R. French (2006). Profitability, investment and average returns. Journal of Financial Economics 82(3), 491 – 518.
Fama, E. F. and K. R. French (2015). A five-factor asset pricing model. Journal of Financial Economics 116(1), 1 – 22.
Fama, E. F. and K. R. French (2020). Comparing cross-section and time-series factor models. Review of Financial Studies 33(5), 1891 – 1926.
Hou, K., H. Mo, C. Xue, and L. Zhang (2019). Which factors? Review of Finance 21(1), 1 – 35.
Hou, K. H. Mo, C. Xue, and L. Zhang (2020). An augmented q-factor model with expected growth. Review of Finance forthcoming.
Hou, K., C. Xue, and L. Zhang (2015). Digesting anomalies: An investment approach. Review of Financial Studies 28(3), 650 – 705.
Jegadeesh, N. and S. Titman (1993). Returns to buying winners and selling losers: Implications for stock market efficiency. Journal of Finance 48(1), 65 – 91.
Novy-Marx, R. (2013). The other side of value: The gross profitability premium. Journal of Financial Economics 108(1), 1 – 28.
Stambaugh, R. F., J. Yu, and Y. Yuan (2015). Arbitrage asymmetry and the idiosyncratic volatility puzzle. Journal of Finance 70(5), 1903 – 1948.
Stambaugh, R. F. and Y. Yuan (2017). Mispricing factors. Review of Financial Studies 30(4), 1270 – 1315.
免責聲明(míng):入市有風險,投資需謹慎。在任何情況下(xià),本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià),本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外,文中圖表均直接或間接來(lái)自于相應論文,僅爲介紹之用(yòng),版權歸原作者和(hé)期刊所有。