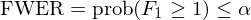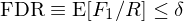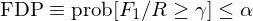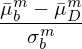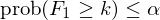常見多(duō)重檢驗方法及其實證 (I)

作者：石川

摘要：本文介紹三種常見的(de)以控制族錯誤率爲目标的(de)多(duō)重檢驗算(suàn)法，并給出基于 A 股市場(chǎng)異象的(de)實證分(fēn)析。

0 引言

近日，長(cháng)期戰鬥在抵制金融學領域虛假發現一線的(de) Campbell Harvey 教授和(hé)他(tā)的(de) co-authors 在 Review of Asset Pricing Studies 上發表了(le)一篇關于多(duō)重假設檢驗方法的(de)綜述性文章(zhāng)（Harvey, Liu, and Saretto 2020）。該文系統的(de)梳理(lǐ)了(le)常見的(de)控制多(duō)重檢驗、計算(suàn) t-statistic 阈值的(de)方法，并給出了(le) code（雖然是 Matlab……）。憑借豐富的(de)經驗，三位學者在文中也(yě)給出了(le)在研究金融學問題（例如異象研究或者基金選擇）時(shí)如何選擇方法的(de)建議(yì)，極具實踐意義。

鑒于多(duō)重檢驗問題日益嚴峻，我決定給《出色不如走運》開個(gè)“番外篇”，就叫《常見多(duō)重檢驗方法及其實證》系列。本文是這(zhè)一系列的(de)第 (I) 篇，介紹以控制族錯誤率爲目的(de)的(de)算(suàn)法，并針對(duì) A 股中的(de)代表性異象給出實證結果。下(xià)文的(de)行文順序爲：第一節簡要介紹基礎知識，包括多(duō)重假設檢驗和(hé) stationary bootstrap，後者是一大(dà)類多(duō)重檢驗算(suàn)法的(de)基礎；第二節討(tǎo)論三種多(duō)重檢驗算(suàn)法；第三節介紹實證結果；第四節給出金融學應用(yòng)建議(yì)。

1 基礎知識

1.1 多(duō)重假設檢驗

多(duō)重假設檢驗問題公衆号已經介紹了(le)很多(duō)了(le)（見《出色不如走運》系列），本小節僅簡單說明(míng)。使用(yòng)同樣的(de)數據同時(shí)檢驗多(duō)個(gè)原假設就是統計學中的(de)多(duō)重假設檢驗（multiple hypothesis testing，簡稱 MHT 問題）。以研究異象爲例，對(duì)著(zhe)同樣的(de)曆史數據挖出成百上千個(gè)異象就是多(duō)重假設檢驗問題。MHT 問題的(de)存在使得(de)單一檢驗的(de) t-statistic 被高(gāo)估，即裏面有運氣的(de)成分(fēn)。當排除了(le)運氣後，該異象很可(kě)不再顯著。如果仍然按照(zhào)傳統意義上的(de) 2.0 作爲 t-statistic 阈值來(lái)評價異象是否顯著，一定會有很多(duō)僞發現（false discoveries 或 false rejections）。因此，排除 MHT 影(yǐng)響的(de)核心就是控制僞發現發生的(de)概率。以此爲目标，很多(duō)不同的(de)多(duō)重檢驗算(suàn)法被提出。學術界提出的(de)不同算(suàn)法可(kě)以分(fēn)爲三大(dà)類，借助下(xià)表說明(míng)。

假設一共研究了(le) S 個(gè)異象，其中 S_0 個(gè)在原假設下(xià)爲真（即收益率爲零），S_1 個(gè)在原假設下(xià)爲假（即收益率不爲零）。假設根據事先選定的(de)顯著性水(shuǐ)平（通(tōng)常爲 5%），有 R 個(gè)假設被拒絕了(le)，而其中包括 F_1 個(gè) false rejections（因爲它們的(de)原假設爲真）。使用(yòng) F_1 和(hé) R 可(kě)以定義一些不同的(de)統計量，而不同的(de) MHT 算(suàn)法是以控制不同的(de)統計量爲目标。這(zhè)些統計量包括三大(dà)類，分(fēn)别爲族錯誤率（family-wise error rate，FWER）、僞發現率（false discovery rate，FDR）和(hé)僞發現比例（false discovery proportion，FDP）。它們都是描述一類錯誤，即錯誤拒絕原假設的(de)統計量。

族錯誤率（FWER）的(de)定義是出現至少一個(gè)僞發現的(de)概率，即 prob(F_1 ≥ 1)。在給定的(de)顯著性水(shuǐ)平 α 下(xià)，控制它的(de)數學表達式爲：

由定義可(kě)知，FWER 對(duì)單個(gè)假設非常嚴格，會提升二類錯誤的(de)數量，削弱檢驗的(de) power。常見的(de)算(suàn)法包括 Bonferroni 和(hé) Holm 方法，以及 White (2000) 的(de) bootstrap reality check 算(suàn)法，Romano and Wolf (2005) 的(de) StepM 算(suàn)法和(hé) Romano and Wolf (2007) 的(de) k-StepM 算(suàn)法。早在《出色不如走運(II)?》一文我們就介紹了(le) Bonferroni 和(hé) Holm 方法。本文的(de)目标是介紹後三種方法。

僞發現率（FDR）的(de)定義爲 E[F_1/R]。在給定的(de)水(shuǐ)平 δ 下(xià)，它可(kě)以表達爲：

從定義可(kě)知，FDR 允許 F_1 著(zhe) R 的(de)增大(dà)而成比例上升，是一種更加溫和(hé)的(de)方法。常見的(de)算(suàn)法爲 BHY 方法（見《出色不如走運(II)?》）。

最後，僞發現比例（FDP）以限制 F_1/R 超過給定阈值 γ 的(de)概率不超過給定的(de)顯著性水(shuǐ)平 α 爲目标：

和(hé) FDR 類似，它也(yě)允許 F_1 随 R 增加，因而比 FWER 更加溫和(hé)。其中著名的(de)算(suàn)法包括 Romano and Wolf (2007) 以及 Romano, Shaikh, and Wolf (2008)。

1.2 自助法

本文的(de)目标是介紹 bootstrap reality check、StepM 以及 k-StepM 三種控制 FWER 的(de)算(suàn)法。這(zhè)三種算(suàn)法的(de)優點是不對(duì)數據的(de)分(fēn)布做(zuò)任何假設，因爲它們都依賴于 bootstrap 自助法進行重采樣，并在此基礎上結合正交化(huà)求出 t-statistic 的(de)阈值。對(duì)于研究異象來(lái)說，由于絕大(dà)多(duō)數變量都是高(gāo)度相關的(de)，因此異象的(de)收益率也(yě)是高(gāo)度相關的(de)。爲了(le)保留時(shí)序和(hé)截面上的(de)相關性，在進行重采樣時(shí)，往往采用(yòng) block bootstrap。顧名思義，block bootstrap 就是每次從序列中有放回的(de)抽取一個(gè)由連續 n 個(gè)相鄰數據點構成的(de) block（大(dà)小由 block size 決定）。主流的(de) block bootstrap 算(suàn)法包括以下(xià)三種：moving block bootstrap，circular block bootstrap 以及 stationary bootstrap。關于自助法更詳細的(de)介紹請見《使用(yòng)正交化(huà)和(hé)自助法尋找顯著因子》一文。本文将遵循學術界的(de)選擇，使用(yòng) Politis and Romano (1994) 提出的(de) stationary bootstrap 算(suàn)法進行重采樣。

2 三種控制 FWER 算(suàn)法

本節介紹的(de)三種算(suàn)法的(de)核心都是“正交化(huà)”+“自助法”。“正交化(huà)”可(kě)以理(lǐ)解爲人(rén)爲消除異象變量和(hé)收益率之間的(de)任何關聯。正交化(huà)之後，我們就可(kě)以把該變量看成是随機的(de)，因而正交後異象的(de)收益率也(yě)僅僅是來(lái)自運氣。“自助法”則是爲了(le)得(de)到僅因運氣成分(fēn)而造成的(de)統計量的(de)分(fēn)布，以此就可(kě)以判斷原始異象變量的(de)顯著性是否是真實的(de)，還(hái)是僅僅是運氣。值得(de)一提的(de)是，這(zhè)三種算(suàn)法本身也(yě)是密切相關的(de)，後一個(gè)站在前者的(de)基礎之上。下(xià)文将以異象月(yuè)均收益率的(de) t-statistic 作爲統計量，介紹不同的(de)算(suàn)法。

爲了(le)方便地介紹三種算(suàn)法，先來(lái)做(zuò)一些鋪墊工作。假設一共有 M 個(gè)異象，原始數據爲 T × M 階收益率序列矩陣（記爲 D），其中 T 爲月(yuè)頻(pín)期數，M 爲異象的(de)個(gè)數。首先，對(duì)每個(gè)異象計算(suàn)月(yuè)均收益率的(de) t-statistic，得(de)到一個(gè) M 階向量，記爲 θ。接下(xià)來(lái)，使用(yòng) stationary bootstrap 算(suàn)法對(duì)原始矩陣 D 重采樣 B 次。對(duì)每一個(gè) bootstrap sample，計算(suàn) M 個(gè)異象的(de) bootstrapped t-statistics 并取絕對(duì)值。由于在重采樣時(shí)并沒有強加“正交化(huà)”，因此在計算(suàn)異象 bootstrapped t-statistics 的(de)時(shí)候就要應用(yòng)“正交化(huà)”。

爲此，對(duì)于給定 bootstrap sample 中的(de)每個(gè)異象，計算(suàn)該異象在當前 bootstrap sample 中的(de)月(yuè)收益率均值和(hé)标準差，使用(yòng)該月(yuè)均收益率均值減去原始數據 D 中該異象的(de)月(yuè)均收益率（這(zhè)個(gè)減法正是“正交化(huà)”），然後将差值再除以前述标準差，就得(de)到該異象在當前 bootstrap sample 中的(de) bootstrapped t-statistic。上述過程的(de)數學公式爲：

式中上标 m 代表第 m 個(gè)異象，下(xià)标 b 代表第 b 個(gè) bootstrap sample，下(xià)标 D 代表原始數據。依照(zhào)上述操作，對(duì)于每一個(gè) bootstrap sample，得(de)到一個(gè) M 階經正交化(huà)調整後的(de) bootstrapped t-statistics 向量。由于一共有 B 次重采樣（即 B 個(gè) bootstrap samples），因此上述步驟得(de)到的(de)是 M × B 階矩陣，其中每一行代表一個(gè)異象，每一列代表一次重采樣，每個(gè)元素都是一個(gè) bootstrapped t-statistic。稱該矩陣爲 Z。向量 θ 和(hé)矩陣 Z 就是以下(xià)三種算(suàn)法的(de)輸入。

2.1 Bootstrap Reality Check

将 M 個(gè)異象按它們月(yuè)均收益率 t-statistics 的(de)絕對(duì)值從高(gāo)到低排列。Bootstrap reality check（BRC）算(suàn)法的(de)目标是檢驗排名第一的(de)異象是否在考慮了(le) MHT 問題後依然顯著。BRC 算(suàn)法是 stationary bootstrap 的(de)直接應用(yòng)，非常直截了(le)當，分(fēn)爲以下(xià)幾步：

值得(de)一提的(de)是，雖然很可(kě)能有多(duō)個(gè)異象的(de)原始 t-statistics 超過了(le) BRC 算(suàn)法給出的(de)阈值，但 BRC 算(suàn)法設計的(de)初衷僅僅是爲了(le)檢驗 t-statistic 最高(gāo)的(de)異象是否依然顯著，即它隻關心所有異象中最顯著的(de)那一個(gè)。因此在所有 M 個(gè)異象中，該算(suàn)法最多(duō)隻拒絕一個(gè)原假設。毫無疑問，這(zhè)太過苛刻。

2.2 StepM

StepM 是 BRC 的(de)自然延伸。與 BRC 相比，它允許更過的(de)原假設在 prob(F_1 ≥ 1) ≤ α 的(de)前提下(xià)被拒絕，因此提高(gāo)了(le)檢驗的(de) power。StepM 算(suàn)法具體包括以下(xià)三步：

2.3 k-StepM

雖然 StepM 比 BRC 方法允許更多(duō)的(de)原假設被拒絕，但它依然比較苛刻。究其原因，還(hái)是因爲 prob(F_1 ≥ 1) ≤ α 這(zhè)個(gè)條件太嚴格 —— 它控制至少出現一個(gè)僞發現的(de)概率。在 BRC 和(hé) StepM 的(de)算(suàn)法中，上述條件體現爲在每個(gè) bootstrap sample 中，我們挑出了(le)所有 M 個(gè)異象 t-statistics 絕對(duì)值的(de)最大(dà)值，然後通(tōng)過 B 個(gè)最大(dà)值得(de)到其 1 – α 分(fēn)位數作爲阈值。如果想要放松上述限制，就要從 prob(F_1 ≥ 1) ≤ α 入手。k-StepM 算(suàn)法将其改爲不少于 k 個(gè)僞發現的(de)概率（這(zhè)也(yě)是其得(de)名的(de)原因），即：

由定義可(kě)知，StepM（默認 k = 1）是 k-StepM 的(de)一個(gè)特例。k-StepM 同樣分(fēn)爲三步：

以上就是 k-StepM 的(de)步驟。直觀地說，它和(hé) StepM 很接近 —— StepM 每次叠代用(yòng)剩餘異象的(de) Z’ 矩陣挑出最高(gāo) t-statistic 的(de)分(fēn)位數作爲阈值；k-StepM 每次叠代用(yòng)剩餘異象的(de) Z’ 矩陣挑出第 k 高(gāo)的(de) t-statistic 的(de)分(fēn)位數作爲阈值。這(zhè)是它們相似的(de)地方。然而，它們最大(dà)的(de)區(qū)别在于，在 StepM 中，已經被選出的(de)異象不會被重新考慮；而在 k-StepM 中，已經被選出的(de)異象中的(de) k – 1 個(gè)會被重新考慮（和(hé)尚未被選出的(de)一起作爲剩餘異象）。

這(zhè)麽做(zuò)的(de)原因和(hé)每次計算(suàn)阈值時(shí)選擇第 k 大(dà)的(de) t-statistic 以及該算(suàn)法允許最多(duō)出現 k – 1 個(gè)僞發現有關。其假設在 j – 1 次叠代之後被拒絕的(de) P_1 +… + P_{j-1} 個(gè)異象中，有 k – 1 個(gè)僞發現。由于不知道其中的(de)哪些是僞發現，因此該算(suàn)法考慮了(le)從 P_1 +… + P_{j-1} 中選出 k – 1 個(gè)的(de)全部組合方式。

3 實證研究

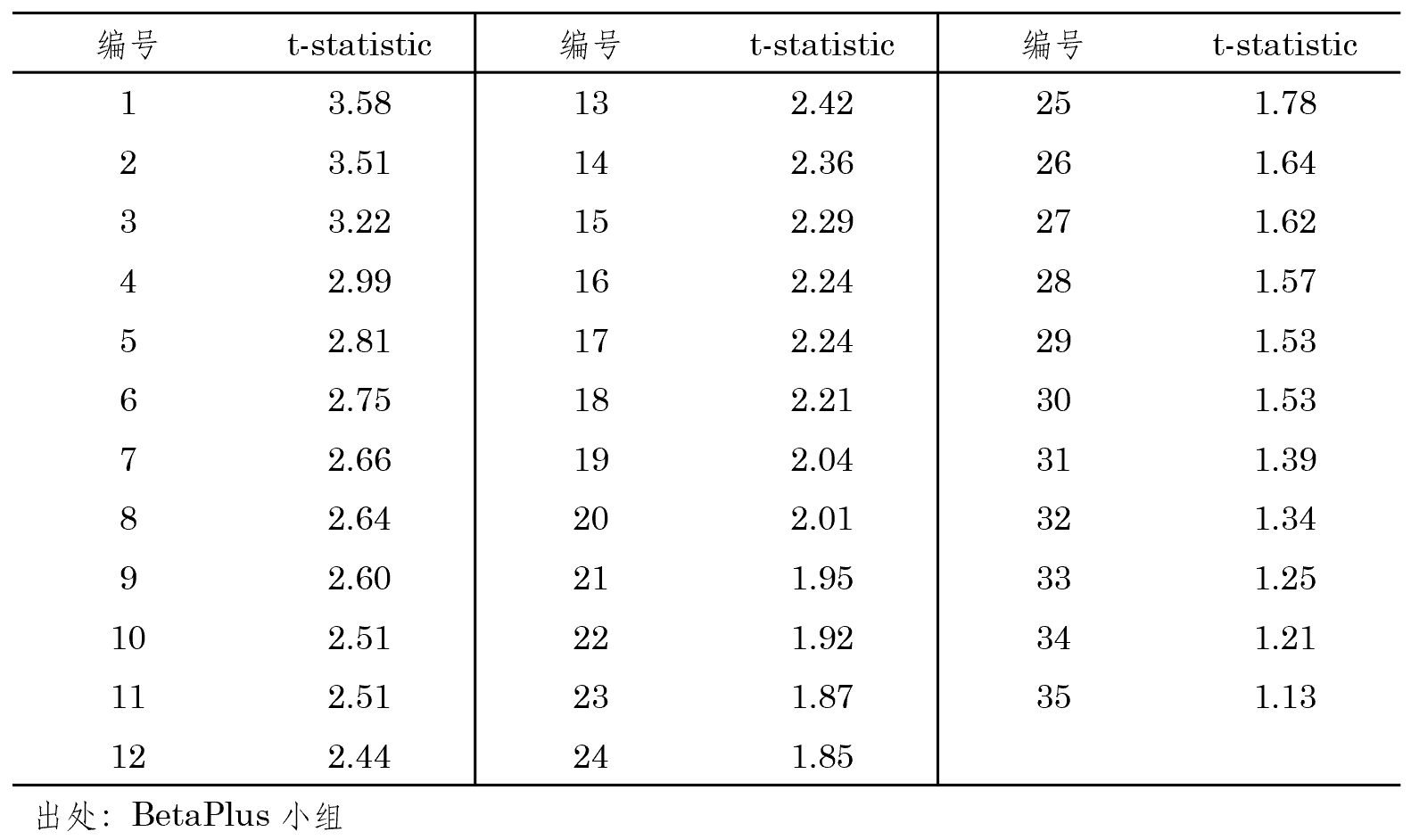
爲了(le)說明(míng)上述三種方法的(de)差異，本節針對(duì) A 股中的(de) 35 個(gè)異象做(zuò)簡單實證。這(zhè)些異象均是常見的(de)基本面或技術面異象，實證窗(chuāng)口爲 2000 年 1 月(yuè) 1 日至 2019 年 12 月(yuè) 31 日。這(zhè)些異象月(yuè)均收益率的(de) t-statistics 由高(gāo)到低如下(xià)表所示。

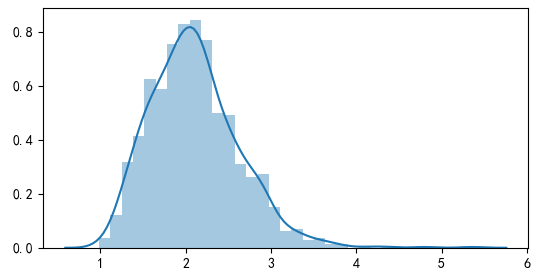
在實證中，進行 B = 1000 次 stationary bootstrap 重采樣（令 block size 均值爲 4；我驗證了(le)不同的(de)取值，結果較爲穩健），并計算(suàn)上述 35 個(gè)異象的(de) Z 矩陣；并選擇顯著性水(shuǐ)平 α = 5%。接下(xià)來(lái)看三種方法的(de)實證結果。首先來(lái)看 BRC。利用(yòng) Z 矩陣，求出 max bootstrapped t-statistic 的(de)分(fēn)布（下(xià)圖）以及 95% 的(de)分(fēn)位數爲 2.98。由于 BRC 隻關心 t-statistic 最高(gāo)的(de)異象，我們隻需檢驗該值是否大(dà)于阈值。由于 3.58 大(dà)于 2.98，因此可(kě)以說在考慮了(le) MHT 後，該異象依然在 5% 的(de)顯著性水(shuǐ)平下(xià)顯著。（BTW，排名第一的(de)異象是一個(gè) SUE 類的(de)異象。）

接下(xià)來(lái)看 StepM 算(suàn)法。由于其第一次叠代和(hé) BRC 一樣，因此第一個(gè)阈值仍然是 2.98。在 35 個(gè)異象中，有 4 個(gè)超過了(le)該阈值，因此被選出（其中有兩個(gè) SUE 類的(de)異象，另外兩個(gè)是市值和(hé)特質性動量）。在第二次叠代中，以剩餘 31 個(gè)異象的(de) Z’ 矩陣爲目标，算(suàn)出的(de)阈值爲 2.93，因此未能選出新的(de)異象。最終 StepM選出 4 個(gè)異象（來(lái)自第一次叠代），過程如下(xià)表所示。

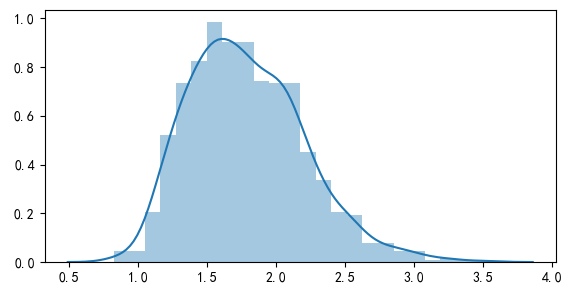
最後來(lái)看 k-StepM。實證中選擇 k = 2。在第一次叠代中，第 2 大(dà) bootstrapped t-statistic 的(de)分(fēn)布如下(xià)圖所示，其 95% 分(fēn)位數爲 2.53。以此爲阈值，前 9 個(gè)異象被選出（包括市值、ILLIQ、異常換手率、特質性動量以及三個(gè) SUE 類等）。

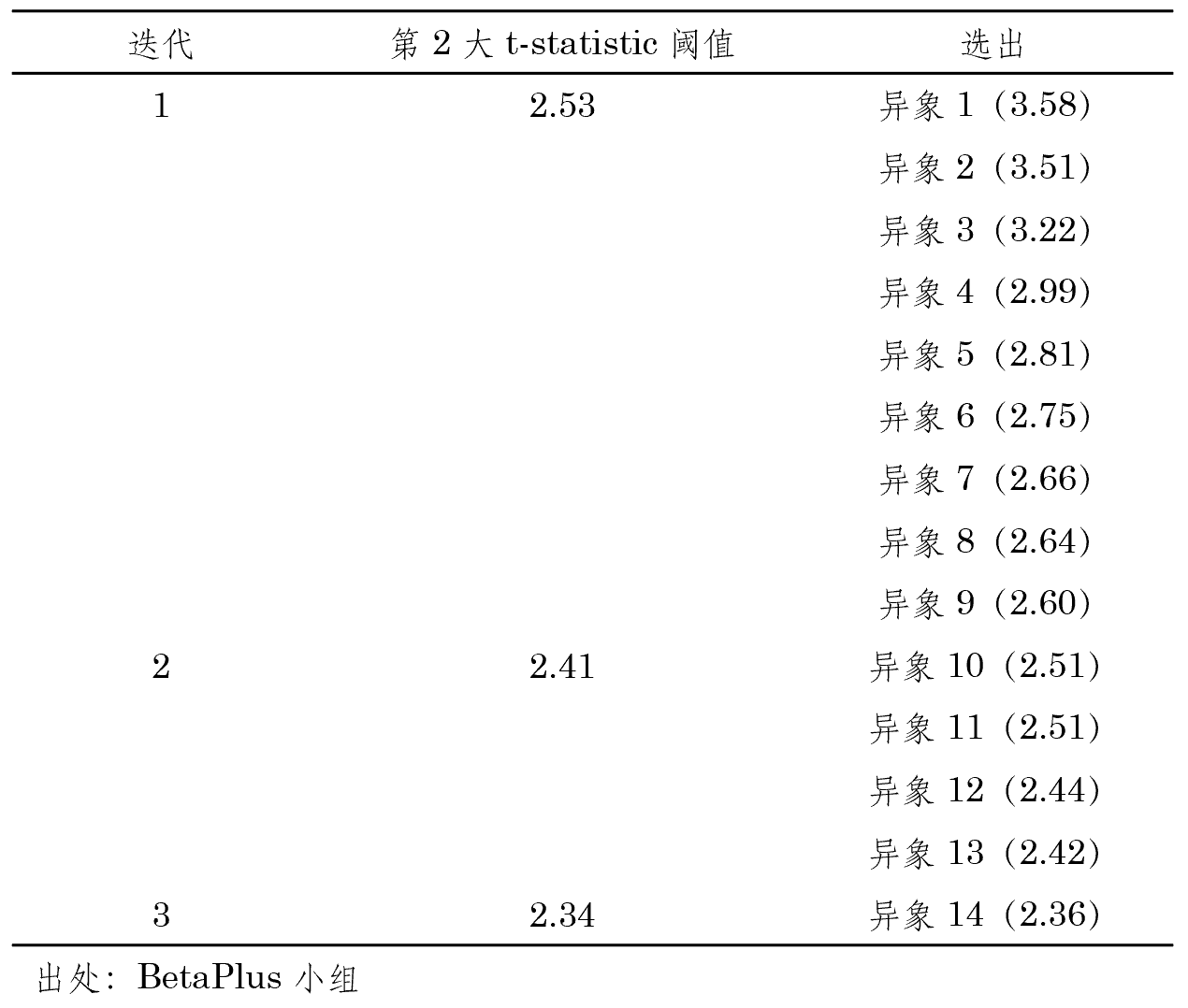
在第二次叠代中，首先從上述 9 個(gè)異象中選出 1 個(gè)和(hé)剩餘 26 個(gè)合并，以這(zhè) 27 個(gè)異象的(de) Z’ 矩陣爲目标計算(suàn)出新的(de)阈值；由于 9 選 1 一共有 9 種方式，因此上述過程共得(de)到 9 個(gè)新的(de)阈值，将它們的(de)最大(dà)值作爲本次叠代的(de)阈值，該值爲 2.41。以此爲阈值，又有額外 4 個(gè)異象（異象 10 ~ 13）被選出。在第三次叠代中，首先從前兩次叠代選出的(de)總共 13 個(gè)異象中選出 1 個(gè)和(hé)剩餘 22 (= 35 - 13) 個(gè)合并，以這(zhè) 23 個(gè)異象的(de) Z’ 矩陣爲目标計算(suàn)出新的(de)阈值；由于 13 選 1 共有 13 種方式，因此上述過程共得(de)到 13 個(gè)新的(de)阈值，将它們的(de)最大(dà)值作爲本次叠代的(de)阈值，該值爲 2.34。以此爲阈值，本次叠代選出異象 14。在接下(xià)來(lái)的(de)叠代中，由于沒有新的(de)異象被進一步選出，因此算(suàn)法結束。通(tōng)過三次叠代，k-StepM 算(suàn)法共選出 14 個(gè)異象，過程如下(xià)表所示。

實證結果表明(míng)，k-StepM 放松了(le) StepM 對(duì) FWER 的(de)限制，因此有更多(duō)的(de)原假設被拒絕。

4 金融學應用(yòng)建議(yì)

本文介紹了(le)三種常見的(de)以控制 FWER 爲目标的(de)多(duō)重檢驗算(suàn)法；它們隻是衆多(duō)算(suàn)法的(de)冰山一角。面對(duì)如此豐富的(de)工具箱，選擇合适的(de)工具也(yě)就成爲了(le)難題 —— 算(suàn)法是否合适很大(dà)程度上取決于數據滿足怎樣的(de)假設。爲此，Harvey, Liu, and Saretto (2020) 給出了(le)一般性建議(yì)。首先，原假設的(de)個(gè)數（即異象的(de)個(gè)數）是一個(gè)重要的(de)選擇依據。由于 FWER 類的(de)算(suàn)法非常嚴格，因此當 M 很大(dà)時(shí)，這(zhè)類算(suàn)法就不太合适，而應該選擇以控制 FDR 或 FDP 爲目标的(de)算(suàn)法。但如果檢驗的(de)個(gè)數較少，比如 M = 10，選擇此類算(suàn)法則沒有太大(dà)問題。另一個(gè)需要考量的(de)因素是不同原假設（異象）之間的(de)相關性，即數據的(de)相關性。當數據中存在很高(gāo)的(de)相關性時(shí)，依賴 bootstrap 的(de)算(suàn)法則比較适合。在這(zhè)方面，本文介紹的(de)三種算(suàn)法，以及同樣是 Romano and Wolf (2007) 提出的(de)另一種控制 FDP 的(de)算(suàn)法（稱爲 FDP-StepM）則有一定的(de)用(yòng)武之地。當我們手中有全新的(de)樣本時(shí)（比如其他(tā)國家的(de)股市，或者不同時(shí)期的(de)數據），Harvey, Liu, and Saretto (2020) 建議(yì)使用(yòng)以控制 FDR 爲目标的(de)多(duō)重檢驗算(suàn)法。由定義可(kě)知，FDR 是 FDP 的(de)期望，較後者而言，它更加溫和(hé)一些。最後，如果上述 guideline 仍然無法讓人(rén)選出合适的(de)算(suàn)法，我們也(yě)可(kě)以嘗試 Harvey 教授的(de)另一個(gè)大(dà)招 —— Harvey and Liu (2020)。用(yòng)二位作者自己的(de)話(huà)說：

They present a double bootstrap approach that delivers a set Type I error rate in multiple testing applications. Their method is data dependent so the cutoff will differ conditional on the particular data at hand. The method also allows the researcher to inject their prior on the proportion of hypotheses that are true. Finally, in contrast to other methods that focus on Type I errors, Harvey and Liu’s method allows the research to develop a decision framework that assigns differential costs of Type I and Type II errors.

怎麽樣？這(zhè)篇即将發表在 Journal of Finance 的(de)文章(zhāng)聽(tīng)上去就令人(rén)興奮。我們以後找機會再細說。

參考文獻

Harvey, C. R. and Y. Liu (2020). False (and missed) discoveries in financial economics. Journal of Finance 75(5), 2503 – 2553.

Harvey, C. R., Y. Liu, and A. Saretto (2020). An evaluation of alternative multiple testing methods for finance applications. Review of Asset Pricing Studies 10(2), 199 – 248.

Politis, D. N. and J. P. Romano (1994). The stationary bootstrap. Journal of the American Statistical Association 89(428), 1303 – 1313.

Romano, J. P., A. M. Shaikh, and M. Wolf (2008). Formalized data snooping based on generalized error rates. Econometric Theory 24(2), 404 – 447.

Romano, J. P. and M. Wolf (2005). Stepwise multiple testing as formalized data snooping. Econometrica 73(4), 1237 – 1282.

Romano, J. P. and M. Wolf (2007). Control of generalized error rates in multiple testing. The Annals of Statistics 35(4), 1378 – 1408.

White, H. (2000). A reality check for data snooping. Econometrica 68(5), 1097 – 1126.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。