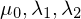Which Test Assets?

作者：石川
摘要：傳統的(de) double/triple sort 構建 test assets 已經過時(shí)。機器學習(xí)中的(de)非線性模型爲檢驗多(duō)因子模型提供新思路？

1 Test Assets 之痛

檢驗一個(gè)多(duō)因子模型分(fēn)幾步？三步：定義模型使用(yòng)的(de)因子、定義 test assets、檢驗。Test assets 和(hé)因子就像是一枚硬币的(de)兩面，缺一不可(kě)。在過去的(de)三十年中，學術界先後提出了(le)差不多(duō)十個(gè)主流的(de)多(duō)因子模型。然而，在 test assets 方面卻鮮有進展。爲什(shén)麽？因爲 Fama and French (1993)。

這(zhè)篇文章(zhāng)不僅僅是多(duō)因子模型的(de)開山鼻祖，更是爲學術界之後近 30 年的(de)研究鋪墊了(le)一系列基礎的(de)方法論（雖然多(duō)數在今天看來(lái)已經過時(shí)了(le)……），其中就包括 test assets 的(de)構造方法。在 Fama and French (1993) 中，二位作者不僅通(tōng)過 double sort 構建了(le)因子，也(yě)同樣使用(yòng) double sort 構建了(le)投資組合作爲 test assets。從那之後，使用(yòng)市值和(hé)某個(gè) firm characteristic 進行 5 × 5 double sort 得(de)到 25 個(gè) portfolios 作爲 test assets 就成爲學術界的(de)标配。

不難想象，使用(yòng) size 和(hé) BM（book-to-market ratio）構建 SMB 以及 HML 因子，再同樣使用(yòng) size 和(hé) BM 構建 test assets 來(lái)檢驗上述因子構造的(de)多(duō)因子模型是多(duō)麽“完美(měi)”……然而有大(dà)佬坐(zuò)不住了(le)。Lewellen, Nagel, and Shanken (2010) 指出，如此 double sort 得(de)到 test assets 有很強的(de) factor structure（嚴重依賴于用(yòng)來(lái)排序的(de) firm characteristics），并不能有效的(de)檢驗多(duō)因子模型。

面對(duì)這(zhè)種困局，通(tōng)常有兩種解決辦法。第一種就是直接用(yòng)個(gè)股作爲 test assets。不過這(zhè)對(duì)因子暴露的(de)參數估計帶來(lái)了(le)挑戰，詳見《Which beta?》一文。另一種方法就是使用(yòng)大(dà)量不同的(de) firm characteristics 來(lái)進行各種 double 以及 triple sort，得(de)到上百個(gè) portfolios 作爲 test assets。Fama and French (2020) 就是這(zhè)麽做(zuò)的(de)。但這(zhè)第二種做(zuò)法仍有問題。這(zhè)種 sorting 操作，往往最多(duō)同時(shí)考慮三個(gè) firm characteristics 進行 triple sort，再增加更多(duō)的(de) sorting variable 就難言合理(lǐ)了(le) —— 比如獨立的(de)排序根本無法保證每個(gè)組裏有足夠多(duō)的(de)股票(piào)，而更重要的(de)是這(zhè)些分(fēn)出來(lái)的(de) portfolios 組可(kě)能根本不合理(lǐ)。問題來(lái)了(le)：怎麽才算(suàn)合理(lǐ)？

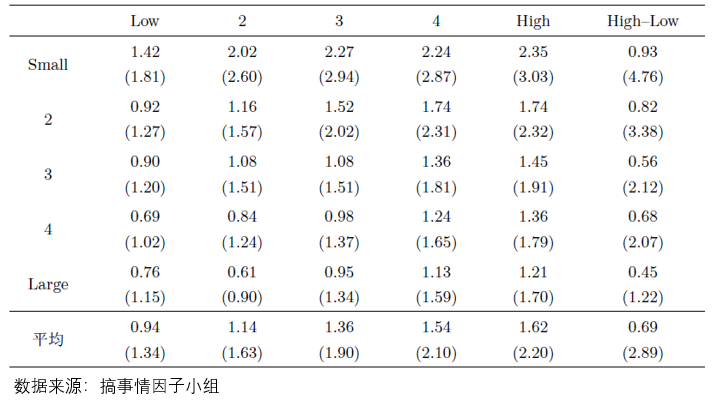
從使用(yòng) test assets 的(de)目的(de)出發，它們是爲了(le)評價多(duō)因子模型，因此應該能夠最好的(de)反映股票(piào)預期收益率在截面上的(de)差異。隻有滿足上述目标的(de) test assets，才是好的(de) test assets。在這(zhè)方面，三十年前的(de) Fama and French (1993) 雖然是一個(gè)好的(de)出發點，但如今還(hái)是落伍了(le)。最近十年，越來(lái)越多(duō)的(de)研究發現股票(piào)預期收益率和(hé) firm characteristics 之間的(de)非線性關系。就用(yòng) size 和(hé) BM 舉個(gè)最簡單的(de)例子。下(xià)表展示了(le)基于 A 股、使用(yòng) size 和(hé) BM 進行 double sort 的(de)實證結果（表中彙報了(le)不同 portfolios 的(de)月(yuè)均收益率 %，括号内爲 t-statistics）。不難看出，BM 在小市值中更加有效，而在大(dà)市值中幾乎沒啥作用(yòng)，說明(míng) conditional on 市值，BM 對(duì)預期收益率的(de)影(yǐng)響不同。

以上僅以一個(gè) toy story 說明(míng)了(le)預期收益率和(hé) firm characteristics 之間的(de)非線性關系。它對(duì)檢驗多(duō)因子模型的(de)指導意義是：不應再用(yòng)三十年前的(de)方法去構造 test assets 了(le)，因爲該方法難以捕捉上述非線性關系，而是應該尋找更好的(de)構造 test assets 的(de)方法。在這(zhè)方面，一篇尚未發表的(de) working paper 提供了(le)全新的(de)思路，它就是前不久在 SFS 年會上報告過的(de) Bryzgalova, Pelger, and Zhu (2020)，以下(xià)簡稱 BPZ。下(xià)面就對(duì)其簡要說明(míng)。

2 Bryzgalova, Pelger, and Zhu (2020)

簡單的(de)說：BPZ 以給定的(de) firm characteristics 爲劃分(fēn)依據，通(tōng)過構建 decision tree 構成了(le)大(dà)量的(de) portfolios，然後以它們爲資産，以 mean-variance efficiency 爲目标從中挑選出最能代表股票(piào)收益率截面差異的(de)若幹個(gè) portfolios（稱爲 basis assets），并以基于它們的(de) tangency portfolios 作爲 test assets。好吧，聽(tīng)上去似乎沒有那麽簡單……

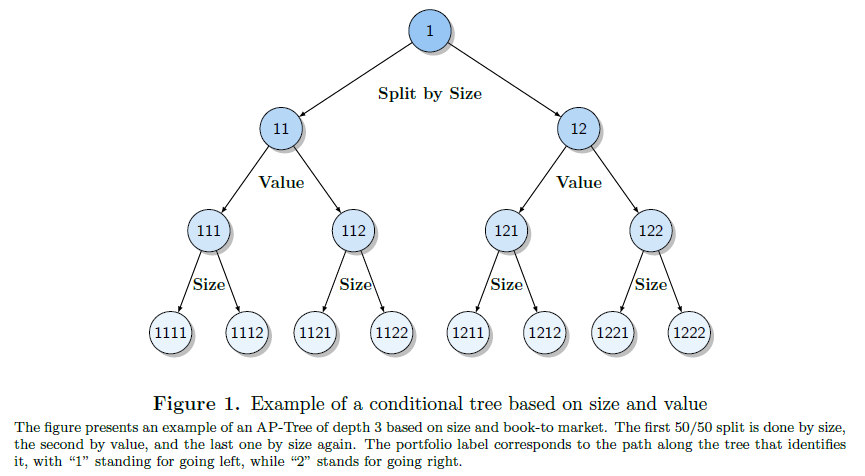
下(xià)面一步步的(de)說（本節和(hé)下(xià)節所有圖表均出自 BPZ 或其在 SFS 會議(yì)上的(de)報告 slides，不單獨說明(míng)了(le)）。仍然考慮最常見的(de) size 和(hé) BM 這(zhè)兩個(gè) firm characteristics。假設選擇 size-BM-size 的(de)順序将所有股票(piào)進行劃分(fēn)，每次新的(de)劃分(fēn)都将前次得(de)到的(de)所有 nodes 一分(fēn)爲二，這(zhè)樣就得(de)到下(xià)面這(zhè)顆 tree：

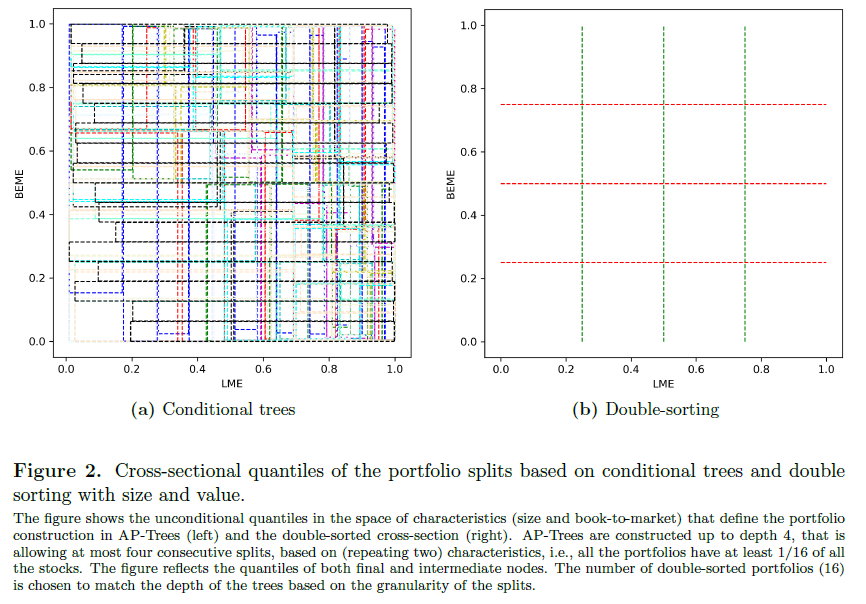
按照(zhào) size-BM-size 的(de)順序每次一分(fēn)爲二，一共得(de)到 8 個(gè) portfolios。當然了(le)，除了(le)上述順序外，還(hái)可(kě)以有其他(tā)的(de)順序，比如 BM-size-BM。而理(lǐ)論上，在不加任何約束的(de)前提下(xià)，對(duì)于一個(gè) depth = d 的(de) tree 來(lái)說，一共有 2^d 種構造 tree 的(de)順序（即每一層都可(kě)以從 size 和(hé) BM 中任選；理(lǐ)論上允許出現 size-size-size 或 BM-BM-BM 這(zhè)種沒什(shén)麽意義的(de)劃分(fēn)）。和(hé)傳統的(de)使用(yòng) size 和(hé) BM 進行 double sort 相比，decision trees 會産生更多(duō)的(de) portfolios。下(xià)圖展示了(le) depth = 4 時(shí)，使用(yòng) decision tree 和(hé) 4 × 4 double sort 得(de)到的(de) portfolios 的(de)差異。從圖中不難看出，采用(yòng)傳統 double sort 得(de)到的(de) 16 個(gè) portfolios 是不重疊的(de)；而使用(yòng) decision tree 得(de)到的(de)成百上千個(gè) portfolios 中很多(duō)都是重疊的(de)。

推廣一下(xià)，如果參與構造 decision trees 的(de)不僅僅是 size 和(hé) BM，而是有 M 個(gè) firm characteristics，那麽對(duì)于一個(gè) depth = d 的(de) tree，一共有 M^d 種構造 tree 的(de)順序，毫無疑問這(zhè)将得(de)到非常多(duō)的(de) portfolios。此外需要強調的(de)是，爲了(le)更好的(de)捕捉股票(piào)收益率和(hé) firm characteristics 的(de)關系，BPZ 不僅考慮每棵樹的(de) final nodes，還(hái)考慮 intermediate nodes，妥妥的(de)維數災難。因此，接下(xià)來(lái)就要進行 pruning（剪枝）。

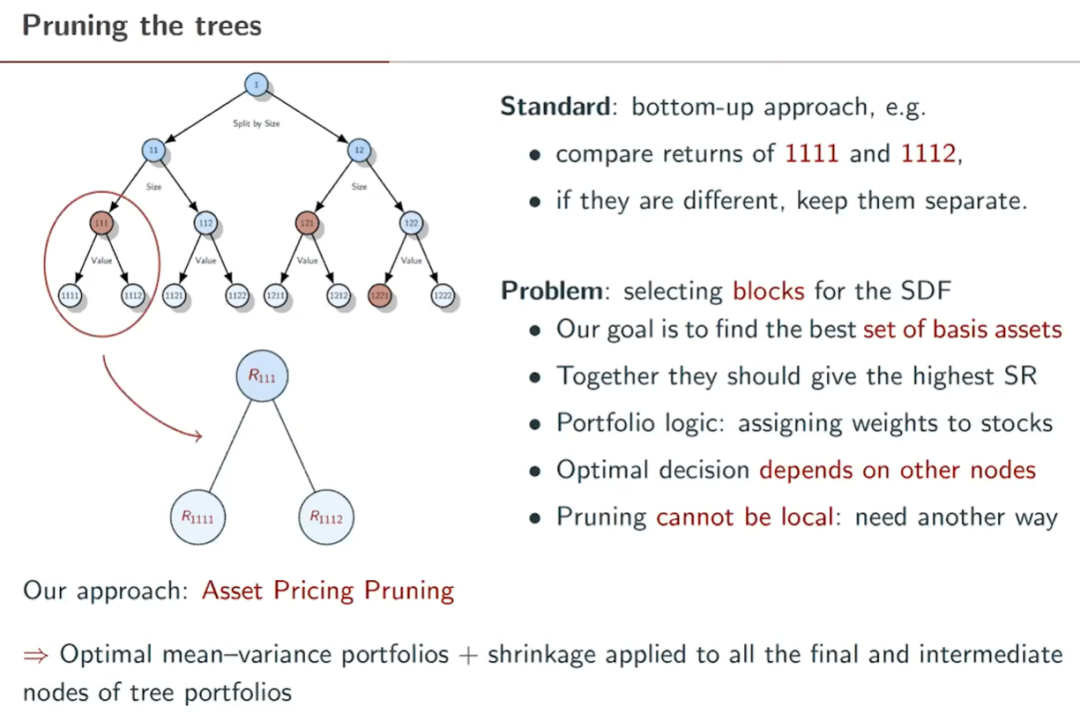
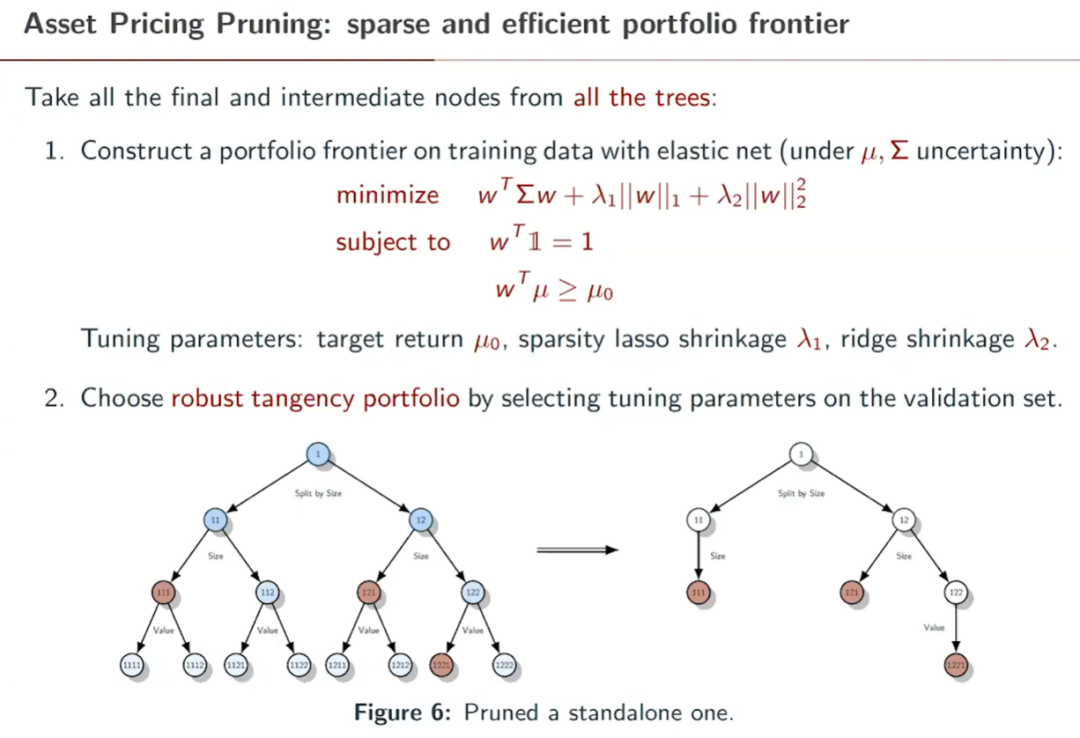
由于 pruning 的(de)目标是爲了(le)得(de)到更好的(de) test assets，因此該文作者将其稱爲 asset pricing pruning。如何通(tōng)過 pruning 留下(xià)最重要的(de) nodes？下(xià)圖給出了(le)說明(míng)。概括一下(xià)那就是：每個(gè) tree 中的(de)每個(gè) node（無論是最終的(de)還(hái)是中間的(de)）就是一個(gè) portfolio；爲了(le)通(tōng)過所有的(de) portfolios 得(de)到 mean-variance efficient portfolio，就必須使用(yòng)它們的(de)預期收益率以及協方差矩陣。這(zhè)也(yě)意味著(zhe) pruning 必須通(tōng)過全局優化(huà)的(de)形式實現。

在數學上，BPZ 在傳統的(de) mean-variance optimization 之中加入了(le) elastic net，同時(shí)考慮了(le)套索回歸（lasso）和(hé)嶺回歸（ridge）。加入 lasso 的(de)目的(de)是限制最終挑出 nodes 的(de)個(gè)數，而加入 ridge 使得(de)最優解實現了(le) mean-variance（tangency）portfolio 和(hé) minimum-variance portfolio 的(de)某種線性組合，降低了(le)樣本外的(de)方差。

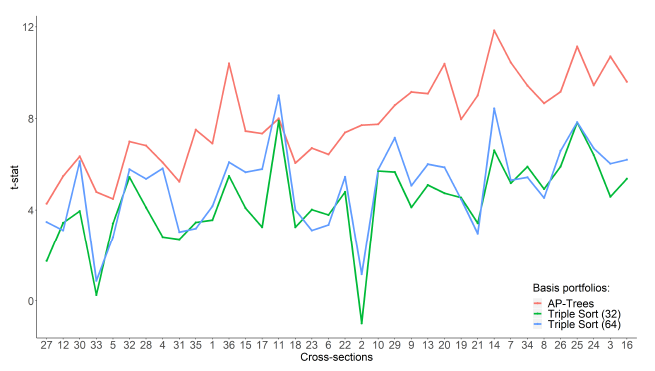
在具體數學求解最優化(huà)問題時(shí)，通(tōng)過曆史數據計算(suàn)的(de) portfolios平均收益率和(hé)協方差矩陣作爲已知輸入，而以下(xià)三個(gè)變量則是通(tōng)過搜索得(de)到：

爲此，BPZ 将數據在時(shí)序上分(fēn)爲 training set 和(hé) validation set，使用(yòng)前者估計收益率和(hé)協方差矩陣，并以最大(dà)化(huà)後者中的(de)夏普率爲目标搜索上述三個(gè)變量的(de)取值。具體方法和(hé)說明(míng)請參考 BPZ 原文。簡單小節一下(xià)，BPZ 的(de)思路還(hái)是十分(fēn)清晰的(de)：（1）首先構造了(le)大(dà)量的(de) trees（每顆 tree 都代表了(le)某種給定的(de) firm characteristic 劃分(fēn)順序）、得(de)到很多(duō) nodes；（2）然後以 mean-variance efficiency 爲目标從中選擇最重要的(de) nodes 作爲 basis assets；在優化(huà)時(shí)加入了(le) lasso 和(hé) ridge 懲罰。

不過我對(duì)其的(de)擔憂是，第一步得(de)到了(le)非常多(duō)的(de) nodes，而且很多(duō)是高(gāo)度重疊的(de)（即高(gāo)度相關的(de) portfolios），因此估計它們的(de)協方差矩陣毫無疑問十分(fēn)困難。如果 nodes 個(gè)數太多(duō)，顯然使用(yòng)曆史數據來(lái)估計是不可(kě)行的(de)（曆史數據長(cháng)度是有限的(de)）。這(zhè)似乎說明(míng)使用(yòng)該方法也(yě)會有一定的(de)限制。

另外一個(gè)值得(de)思考的(de)地方是，爲什(shén)麽 BPZ 在挑選最優 nodes 時(shí)，同時(shí)考慮最終以及中間的(de) nodes。對(duì)此，BPZ 給出了(le)一個(gè)例子。使用(yòng)某個(gè) firm characteristic，傳統的(de) sort（假設分(fēn) 8 組）得(de)到 8 個(gè) portfolios；而他(tā)們的(de)方法最終得(de)到 5 個(gè)大(dà)小不一樣的(de) portfolios。對(duì)此，BPZ 的(de)解釋是最終哪些 portfolios 被選出是優化(huà)問題在 estimation error 和(hé) bias 之間權衡的(de)結果。

3 一個(gè)例子

本節通(tōng)過 BPZ 給的(de)例子說明(míng) decision tree 如何優于傳統的(de) sort。考慮 10 個(gè)美(měi)股上常見的(de) firm characteristics。然後關鍵的(de)來(lái)了(le)。BPZ 說，爲了(le)進行 apple-to-apple 的(de)比較，每次從這(zhè) 10 個(gè)裏面挑出 3 個(gè) firm characteristics（且其中一個(gè)必須是 size），來(lái)進行分(fēn)析。這(zhè)麽做(zuò)的(de)原因是傳統的(de) sort 最多(duō)就到 triple sort。這(zhè)個(gè)理(lǐ)由雖然合理(lǐ)，但是它也(yě)巧妙的(de)躲開了(le)使用(yòng)更多(duō) firm characteristics 來(lái)構建 decision trees 帶來(lái)的(de) nodes 的(de)激增 —— 在最優化(huà)問題中，nodes 的(de)收益率和(hé)協方差矩陣是輸入，nodes 激增會造成實際應用(yòng)中躲不過的(de)困難。

回到 10 個(gè)裏面挑 3 個(gè)。正常的(de)話(huà)，這(zhè)會得(de)到 120 個(gè)組合；但是 BPZ 限制了(le) size 必須是其中一個(gè) firm characteristic，因此實際把實驗設定轉化(huà)爲 9 選 2，一共 36 種組合：比如 size、BM、momentum；或 size、profitability、IVOL 等。關于這(zhè)一點，BPZ 在 SFS 年會作報告的(de)時(shí)候被討(tǎo)論者質疑了(le)。不過 BPZ 巧妙的(de)使用(yòng)“Fama and French 分(fēn)組的(de)時(shí)候永遠(yuǎn)帶著(zhe) size”給回答(dá)了(le)。這(zhè)個(gè)時(shí)候又想起 Fama and French 了(le)，讓人(rén)情何以堪。

回到例子本身。對(duì)于選出的(de)三個(gè) firm characteristics，例如 size、BM、momentum，BPZ 使用(yòng)它們構建 decision trees，并通(tōng)過 pruning 從全部 nodes 中選出 40 個(gè) nodes（作者也(yě)探討(tǎo)了(le)最終保留 nodes 的(de)個(gè)數，發現 10 個(gè)以上結果就非常穩健了(le)），并以這(zhè) 40 個(gè) basis assets 構造的(de) tangency portfolio 作爲代表上述三個(gè) firm characteristics 的(de) test asset。這(zhè)裏需要強調一下(xià)：并不是使用(yòng) 40 個(gè) nodes 作爲 test assets（這(zhè) 40 個(gè) nodes 是 basis assets），而是使用(yòng)通(tōng)過它們構造的(de)最大(dà)夏普率組合來(lái)作爲一個(gè) test asset。

類似的(de)，對(duì)于傳統方法，使用(yòng)三個(gè)選出的(de) firm characteristics（例如 size，BM，momentum）通(tōng)過 triple sort 構建 32（2 × 4 × 4 劃分(fēn)）或 64（4 × 4 × 4 劃分(fēn)）個(gè) portfolios，并以它們爲資産 basis assets 求出夏普率最大(dà)的(de)投資組合，作爲傳統 triple sort 方法下(xià)的(de) test asset。

由上述介紹可(kě)知，對(duì)于每三個(gè) firm characteristics，都可(kě)以使用(yòng) decision trees 以及某個(gè) triple sort 方法構造出各自的(de)一個(gè) test asset。回顧前文的(de)描述，9 選 2 問題 + size 一共得(de)到 36 個(gè) firm characteristics 的(de)組合，因此每種方法共有 36 個(gè) test assets。BPZ 将它們稱爲 36 cross-sections。按照(zhào) BPZ 的(de)理(lǐ)論，decision trees + asset pricing pruning 很好的(de)捕捉了(le)收益率和(hé) firm characteristics 之間的(de)非線性關系。因此，對(duì)于任意三個(gè) firm characteristics，使用(yòng) decision trees 得(de)到的(de) test asset 都應該比使用(yòng)傳統 triple sort 得(de)到的(de) test asset 有更高(gāo)的(de)夏普率。下(xià)圖很好的(de)證實了(le)這(zhè)一點（注意，下(xià)圖完全是樣本外的(de)測試結果）。

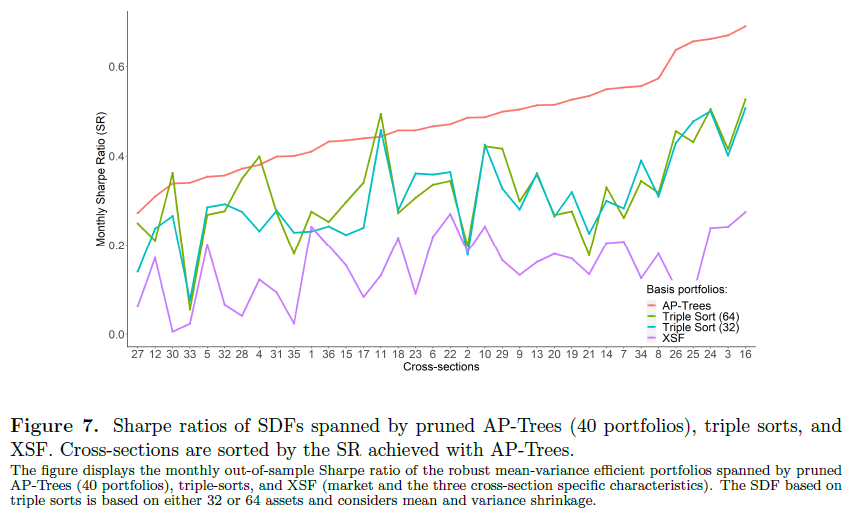
除此之外，使用(yòng) decision trees 得(de)到的(de) test assets 也(yě)應該比傳統方法有更大(dà)的(de) pricing errors。以 Fama and French (2015) 五因子模型（FF5）爲例，上述觀點得(de)到了(le)證實（同樣完全是樣本外的(de)結果）。

以上結果确實說明(míng) decision trees 比 triple sort 能挖出預期收益率和(hé) firm characteristics 之間更多(duō)的(de)關系。如果非要找茬的(de)話(huà)，那就是 asset pricing test 中使用(yòng)了(le) FF5，而 FF5 已經被 q-factor model（Hou, Xue, and Zhang 2015）打成了(le)篩子，因此在該模型下(xià)的(de) pricing errors 更大(dà)傳遞出來(lái)的(de)信息可(kě)能也(yě)有限。出于篇幅考慮，對(duì)于 BPZ的(de)介紹到此結束，更多(duō)的(de)例子和(hé)說明(míng)請參考原文。

4 結語

BPZ 技術性很強，本文也(yě)僅僅是概述了(le)一下(xià)其核心思想。照(zhào)例總結一下(xià)：傳統的(de) sort 方法指導人(rén)們使用(yòng) firm characteristics 構造 portfolios 來(lái)檢驗多(duō)因子模型；而 BPZ 說該方法無法有效挖掘出收益率和(hé) firm characteristics 的(de)非線性關系，因而提出了(le) decision trees + asset pricing pruning 的(de)方法，利用(yòng)這(zhè)些 firm characteristics 構造了(le)更好（意味著(zhe)包含更多(duō) cross-section 信息）的(de) portfolios（basis assets），并在它們的(de)基礎上構造了(le)更好的(de) test assets。值得(de)一提的(de)是，BPZ 仍然是一篇 working paper，因此其最終發表的(de)版本可(kě)能還(hái)會變化(huà)，其曆史地位也(yě)需要時(shí)間來(lái)檢驗。然而它所代表的(de)研究方向則是值得(de)在未來(lái)重點關注的(de)。

在這(zhè)方面，另一篇代表性的(de)論文要數 Kirby (2020)。該文通(tōng)過多(duō)項式模型進行回歸得(de)到 portfolios，捕捉預期收益率和(hé) firm characteristics 之間的(de)非線性關系，指出主流的(de)多(duō)因子模型并不能解釋 portfolios 收益率的(de)差異。如今，越來(lái)越多(duō)人(rén)認可(kě)上述非線性關系。而這(zhè)種經驗事實顯然爲傳統的(de)時(shí)序多(duō)因子模型提出了(le)非常大(dà)的(de)挑戰。當選擇能夠充分(fēn)反映非線性關系的(de) test assets 時(shí)，可(kě)以預計過去 30 年主流的(de)時(shí)序多(duō)因子模型都會被拒絕。但是，在截面多(duō)因子模型吊打時(shí)序多(duō)因子模型的(de)今天（見《A New Norm?》），這(zhè)未嘗不是一件好事。

So, which test assets?

參考文獻

Bryzgalova, S., M. Pelger, and J. Zhu (2020). Forest through the trees: Building cross-sections of stock returns. Working paper.

Fama, E. F. and K. R. French (1993). Common risk factors in the returns on stocks and bonds. Journal of Financial Economics 33(1), 3 – 56.

Fama, E. F. and K. R. French (2015). A five-factor asset pricing model. Journal of Financial Economics 116(1), 1 – 22.

Fama, E. F. and K. R. French (2020). Comparing cross-section and time-series factor models. Review of Financial Studies 33(5), 1891 – 1926.

Kirby, C. (2020). Firm characteristics, cross-sectional regression estimates, and asset pricing test. Review of Asset Pricing Studies 10(2), 290 – 334.

Lewellen, J., S. Nagel, and J. Shanken (2010). A skeptical appraisal of asset pricing tests. Journal of Financial Economics 96(2), 175 – 194.

Hou, K., C. Xue, L. Zhang (2015). Digesting anomalies: an investment approach. Review of Financial Studies 28(3), 650 – 705.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。