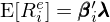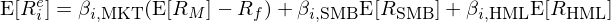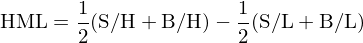A New Norm?

作者：石川
摘要：自 Fama and French (1993) 以來(lái)，所有主流的(de)多(duō)因子模型都是時(shí)序回歸模型。然而，27 年後的(de)今天，一場(chǎng)變革正悄然發生。

0 引言

線性多(duō)因子模型假設資産的(de)預期（超額）收益由資産對(duì)因子的(de)暴露和(hé)因子的(de)預期收益率決定，即它們滿足如下(xià)關系：

其中 E[R_i^e] 表示資産 i 的(de)預期（超額）收益，β_i 爲資産 i 的(de)因子暴露向量，λ 表示因子預期收益向量，因子預期收益率也(yě)稱爲因子風險溢價（risk premium）。在關于多(duō)因子模型的(de)研究中，一旦因子被确定，估計它們的(de) risk premium 就是最核心的(de)問題（之一）。在這(zhè)方面，學術界過去近 30 年的(de)範式當屬時(shí)間序列回歸因子模型（time-series regression factor models）。

1 時(shí)序回歸因子模型

20 世紀 90 年代，Fama and French (1993) 三因子模型（以下(xià)稱爲 FF3）問世，取代 CAPM 成爲資産定價的(de)基準。對(duì)于股票(piào)市場(chǎng)而言，FF3 在市場(chǎng)因子的(de)基礎上加入了(le) SMB 和(hé) HML 代表的(de)規模和(hé)價值因子：

由于是第一個(gè)多(duō)因子模型，Fama and French (1993) 對(duì)學術界之後在實證資産定價方面的(de)研究影(yǐng)響十分(fēn)深遠(yuǎn)。在這(zhè)之後的(de)近 30 年裏，縱然有很多(duō)經典的(de)多(duō)因子模型被提出 —— 包括 Carhart (1997) 四因子模型（它在 FF3 的(de)基礎上加入了(le)截面動量），2015 年前後充滿恨怨情仇的(de) Fama and French (2015) 五因子模型以及 Hou, Xue, and Zhang (2015) 的(de) q-factor model，以及 2018 年前後從行爲金融學角度提出的(de) Stambaugh and Yuan (2017) 以及 Daniel, Hirshleifer, and Sun (2020) 模型，但它們無疑不是遵循了(le) FF3 的(de)思路：

由于在檢驗資産 pricing errors 的(de)時(shí)候采用(yòng)了(le)時(shí)序回歸（同時(shí)得(de)到因子暴露 β 的(de)估計以及 pricing error，即截距項），學術界把按上述方法構建的(de)多(duō)因子模型稱爲時(shí)間序列回歸因子模型。在上述第二步檢驗多(duō)因子模型的(de)過程中，資産采用(yòng)的(de)是投資組合，而非個(gè)股。這(zhè)麽做(zuò)的(de)主要原因是，所有模型都是不完美(měi)的(de)，隻要使用(yòng)足夠多(duō)的(de) test assets 來(lái)檢驗模型，那麽它們的(de) pricing errors 一定會顯著不爲零。這(zhè)意味著(zhe)使用(yòng)個(gè)股作爲資産的(de)話(huà)，多(duō)因子模型一定會被拒絕（over-rejection）。

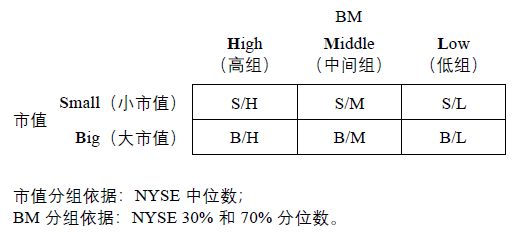
在 FF3 使用(yòng)的(de)方法中，更值得(de)思考的(de)其實是第一步，即使用(yòng) portfolio sort 得(de)到的(de)投資組合作爲因子投資組合，以其收益率的(de)時(shí)序均值來(lái)估計并檢驗因子 risk premium。以 FF3 的(de) HML 因子爲例，它使用(yòng)市值和(hé) book-to-market ratio（BM）進行 double sort 來(lái)構建因子投資組合：

上式中，HML 就是通(tōng)過 double sort 得(de)到的(de)價值因子投資組合，計算(suàn)其收益率并在時(shí)序上取平均，以此檢驗價值因子的(de) risk premium。雖然 portfolio sort 簡單直觀，但通(tōng)過它來(lái)構建因子模拟組合是粗糙的(de) —— 比如無法控制該組合在其他(tā)因子上的(de)暴露。因此按照(zhào)上述方法估計和(hé)檢驗因子的(de) risk premium 也(yě)存在改進空間。在這(zhè)方面，學術界更加認可(kě)的(de)方法是 Fama and MacBeth (1973) 提出的(de) two-pass regression。

2 截面回歸因子模型

Fama and MacBeth (1973) regression（下(xià)稱 FM regression）是檢驗因子 risk premium 的(de)常見方法。它是一個(gè)“兩步法”：第一步通(tōng)過時(shí)序回歸确定資産的(de)因子暴露，而第二步進行在每個(gè)時(shí)刻 t 進行截面回歸确定 t 時(shí)刻的(de)因子收益率。（需要背景知識的(de)小夥伴請參考《多(duō)因子模型的(de)回歸檢驗》。）相對(duì)于 portfolio sort，截面多(duō)元回歸的(de)好處是，可(kě)以控制其他(tā)變量的(de)影(yǐng)響，更準确的(de)估計因子的(de) risk premium。

在使用(yòng) FM regression 時(shí)，一個(gè)重要的(de)前提的(de)确定資産的(de)因子暴露。由于真實因子暴露是未知的(de)，因此第二步截面回歸存在 errors-in-variables（EIV）問題。爲了(le)盡可(kě)能排除這(zhè)個(gè)問題的(de)影(yǐng)響，Fama and MacBeth (1973) 使用(yòng)投資組合而非個(gè)股作爲 test assets，通(tōng)過時(shí)序回歸得(de)到它們的(de)因子暴露，再進行截面回歸。然而，Jegadeesh et al. (2019) 指出使用(yòng)投資組合而非個(gè)股作爲 test assets 是一種降維處理(lǐ)，投資組合會丢掉很多(duō)個(gè)股截面上的(de)特征。如果待檢驗的(de)因子和(hé)這(zhè)些 test assets 的(de)分(fēn)組屬性正交，用(yòng)它們作爲被解釋變量進行 FM regression 則無法發現這(zhè)些因子的(de) risk premium；該文提議(yì)使用(yòng)個(gè)股作爲資産來(lái)估計和(hé)檢驗因子 risk premium 并給出了(le)解決 EIV 問題的(de)辦法。《Which Beta?》一文曾對(duì)此進行過詳細介紹。

從計量經濟學的(de)角度來(lái)說，使用(yòng)個(gè)股作爲資産進行截面回歸、檢驗因子 risk premium 的(de)時(shí)候，一個(gè)難題是 N > T（即資産的(de)個(gè)數 N 通(tōng)常超過時(shí)序期數 T）對(duì)于檢驗造成的(de)挑戰：

When N is large and T is small, the asymptotic distribution of any traditional risk premium estimator provides a poor approximation to its finite-sample distribution, thus rendering the statistical inference problematic.

一篇最新發表于 Review of Financial Studies 上的(de)文章(zhāng) Raponi, Robotti, and Zaffaroni (2020) 提出了(le) N > T 情況下(xià)的(de) risk premium estimator，很好的(de)應對(duì)了(le)上述問題。（順便一提，這(zhè)篇文章(zhāng)的(de)文獻綜述部分(fēn)對(duì)于學術界提出的(de)不同 risk premium estimators 進行了(le)很好的(de)梳理(lǐ)。）除了(le)将他(tā)們的(de) estimator 用(yòng)于 two-pass regression、檢驗因子 risk premium 外，該文同樣探索了(le)使用(yòng) firm characteristics vs 使用(yòng)時(shí)序回歸 β 作爲因子暴露的(de)差異。該文的(de)結論是，比起時(shí)序回歸 β，公司特征能夠更好的(de)解釋股票(piào)預期收益率的(de)截面差異，這(zhè)一結論和(hé) Chordia, Goyal, and Shanken (2015) 相同。

We show that our large cross-sectional framework poses a serious challenge to common empirical findings regarding the validity of beta-pricing models. In the context of pricing models with Fama-French factors, firm characteristics are found to explain a much larger proportion of variation in estimated expected returns than betas.

梳理(lǐ)一下(xià)本節寫到現在的(de)邏輯。學術界傾向使用(yòng) FM regression 代替 portfolio sort 檢驗因子 risk premium；而在 FM regression 中應使用(yòng)個(gè)股而非個(gè)股的(de)投資組合作爲 test assets（需要解決 EIV 以及 N > T 等問題）；當以個(gè)股爲資産時(shí)，發現公司特征而非時(shí)序回歸 β 作爲因子暴露時(shí)，因子才被定價（顯著的(de) risk premium）且公司特征（而非時(shí)序回歸 β）能夠解釋個(gè)股預期收益率的(de)截面差異。沿著(zhe)這(zhè)個(gè)邏輯，一類新的(de)多(duō)因子模型應運而生，它就是以公司特征爲因子暴露、通(tōng)過截面回歸計算(suàn)因子 risk premium 的(de)截面回歸多(duō)因子模型（cross-section regression factor models）。那麽，截面多(duō)因子模型是否比時(shí)序多(duō)因子模型更好呢(ne)？

Fama and French (2020) 回答(dá)了(le)這(zhè)個(gè)問題（見前文《Which Beta (II)?》）。其核心結論是，比起傳統的(de)時(shí)序回歸多(duō)因子模型，在采用(yòng)截面回歸多(duō)因子模型時(shí)，資産的(de) pricing errors 更接近零，說明(míng)後者比前者更優。此外，當采用(yòng)截面回歸多(duō)因子模型式，因子暴露應采用(yòng)時(shí)變的(de)公司特征，而非恒定的(de)公司特征。此外，Fama and French (2020) 還(hái)研究了(le)一個(gè)“四不像”模型，即使用(yòng)截面回歸計算(suàn)因子 risk premium，得(de)到因子收益率後再通(tōng)過股票(piào)和(hé)因子收益率時(shí)序回歸計算(suàn)股票(piào)的(de)因子暴露，以此取代公司特征。這(zhè)個(gè)“四不像”模型的(de)表現和(hé)時(shí)序回歸模型類似，均不如截面回歸模型。這(zhè)說明(míng)截面回歸模型優于時(shí)序模型的(de)原因可(kě)能源于兩點：（1）截面回歸的(de)因子收益率優于時(shí)序回歸模型中通(tōng)過 portfolio sort 計算(suàn)的(de)因子收益率；（2）使用(yòng)時(shí)變公司特征作爲因子暴露比時(shí)序回歸 β 更優。

關于上述第二點，我們可(kě)以從以下(xià)兩點進行思考：（1）在使用(yòng)個(gè)股進行時(shí)序回歸計算(suàn)因子暴露時(shí)，往往采用(yòng)日頻(pín)收益率數據。由于其噪聲較大(dà)，因此因子暴露的(de)估計會有較大(dà)誤差，使得(de)因子暴露在時(shí)序上不穩定。一旦發生這(zhè)種情況，就會導緻該因子的(de)表現看上去就和(hé)随機因子一樣，因此難以獲得(de)顯著的(de) risk premium。（2）真實的(de)因子暴露未知，公司特征相比于時(shí)序回歸 β 是其更好的(de)代理(lǐ)變量。

3 新範式 ？

自從 Fama and French (1993) 三因子模型問世以來(lái)，學術界便采用(yòng)了(le)時(shí)序回歸多(duō)因子模型這(zhè)一傳統。而 27 年後的(de)今天，Eugene Fama 和(hé) Kenneth French 又通(tōng)過 Fama and French (2020) 一文打破了(le)這(zhè)個(gè)傳統，引領了(le)今後實證資産定價的(de)研究方向。在 Review of Financial Studies 2020 年五月(yuè)的(de)特刊（Special issues: new methods in the cross-section）中，比較時(shí)序和(hé)截面兩種多(duō)因子模型就是其包含的(de)三個(gè)前沿方向之一。雖然 Fama and French (2020) 的(de)結果更多(duō)的(de)建立在純粹的(de)實證分(fēn)析之上，但該文還(hái)是清晰地回答(dá)了(le)學術界和(hé)業界都非常關心的(de)問題：如何估計和(hé)檢驗因子 risk premium；如何選擇因子暴露。從本文第二節提及的(de)衆多(duō)最新研究來(lái)看，使用(yòng) firm characteristics 作爲因子暴露、使用(yòng)截面回歸來(lái)估計和(hé)檢驗因子 risk premium 在未來(lái)一定大(dà)有可(kě)爲。

提起最近十年來(lái)最重要的(de)線性多(duō)因子模型，可(kě)能人(rén)們會首推 Fama and French (2015) 五因子模型。而 Hou, Xue, and Zhang (2015) 的(de) q-factor model 大(dà)概是唯一能夠與之争鋒的(de)。（關于這(zhè)兩個(gè)模型的(de)曆史，見《q-factor model 一段往事》、《從 Factor Zoo 到 Factor War，實證資産定價走向何方?》。）2019 年，Hou et al. (2019) 在 Review of Finance 上以 Which factors? 爲題對(duì)所有主流的(de)時(shí)序多(duō)因子模型進行了(le)比較。除本文第一節提到的(de)模型外，參加對(duì)比的(de)還(hái)包括他(tā)們自己在 q-factor model 基礎上提出的(de) q5 模型（Hou et al. 2020）。一番比較下(xià)來(lái)，以異象投資組合的(de) pricing errors 來(lái)評價，q 和(hé) q5 模型完勝，說明(míng)它們能夠解釋更多(duō)的(de)異象（特别的(de)是，FF5 在 q 和(hé) q5 模型面前不堪一擊）。Hou et al. (2019) 一文也(yě)獲得(de)了(le) 2019 年 Spangle IQAM Best Paper Prize。這(zhè)個(gè)成就也(yě)讓 q 和(hé) q5 模型著(zhe)實揚眉吐氣了(le)一番，它似乎宣告了(le) q/q5 對(duì)于 FF5 的(de)壓倒性勝利。然而，正當我們認爲風向已經發生了(le)變化(huà)，并準備開始接納 q/q5 代替 FF5 作爲未來(lái)實證資産定價研究中的(de) benchmark 的(de)時(shí)候，Fama and French (2020) 橫空出世，直接“斃”了(le)所有的(de)時(shí)序多(duō)因子模型，指出以 firm characteristic 爲因子暴露代理(lǐ)變量的(de)截面多(duō)因子模型才是未來(lái)。

你品，你細品。

參考文獻

Carhart, M. M. (1997). On persistence in mutual fund performance. Journal of Finance 52(1), 57 – 82.

Chordia, T., A. Goyal, and J. A. Shanken (2015). Cross-sectional asset pricing with individual stocks: Betas versus characteristics. Working paper.

Daniel, K. D., D. A. Hirshleifer, and L. Sun (2020). Short- and long-horizon behavioral factors. Review of Financial Studies 33(4), 1673 – 1736.

Fama, E. F. and K. R. French (1993). Common risk factors in the returns on stocks and bonds. Journal of Financial Economics 33(1), 3 – 56.

Fama, E. F. and K. R. French (2015). A five-factor asset pricing model. Journal of Financial Economics 116(1), 1 – 22.

Fama, E. F. and K. R. French (2020). Comparing cross-section and time-series factor models. Review of Financial Studies 33(5), 1891 – 1926.

Fama, E. F. and J. D. MacBeth (1973). Risk, return, and equilibrium: Empirical tests. Journal of Political Economy 81(3), 607 – 636.

Hou, K., H. Mo, C. Xue, and L. Zhang (2019). Which factors? Review of Finance 21(1), 1 – 35.

Hou, K., H. Mo, C. Xue, and L. Zhang (2020). An augmented q-factor model with expected growth. Review of Finance forthcoming.

Hou, K., C. Xue, and L. Zhang (2015). Digesting anomalies: An investment approach. Review of Financial Studies 28(3), 650 – 705.

Jegadeesh, N., J. Noh, K. Pukthuanthong, R. Roll, and J. Wang (2019). Empirical tests of asset pricing models with individual assets: Resolving the errors-in-variables bias in risk premium estimation. Journal of Financial Economics 133(2), 273 – 298.

Raponi, V., C. Robotti, and P. Zaffaroni (2020). Testing beta-pricing models using large cross-sections. Review of Financial Studies 33(6), 2796 – 2842.

Stambaugh, R. F. and Y. Yuan (2017). Mispricing factors. Review of Financial Studies 30(4), 1270 – 1315.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。