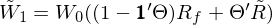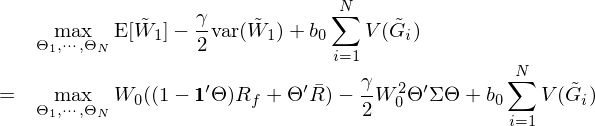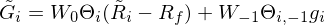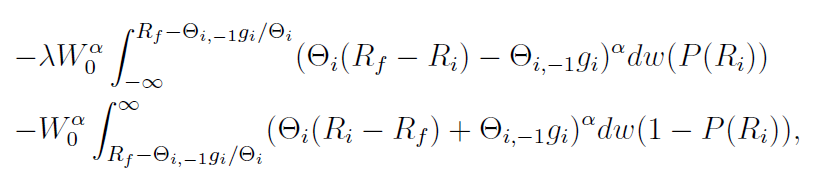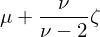前景理(lǐ)論與股票(piào)收益 (II)

作者：石川
摘要：本文解讀 Barberis, Jin, and Wang (2019)。

1 前情回顧

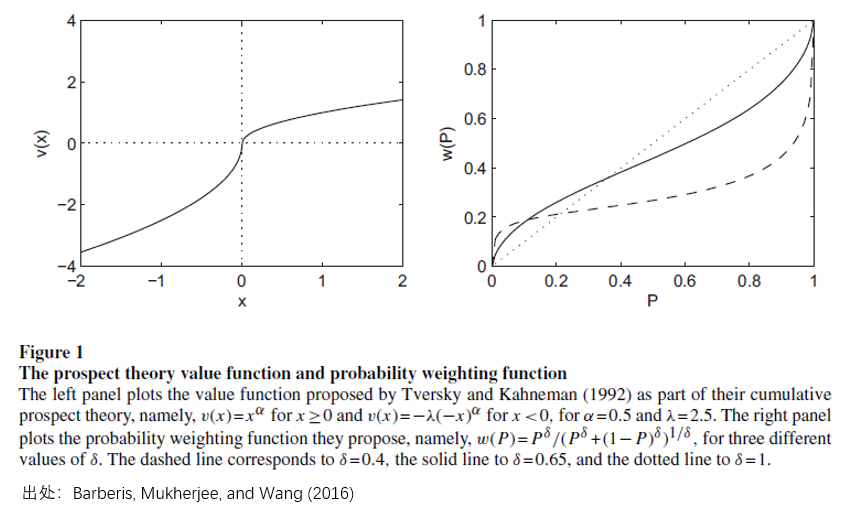
前文《前景理(lǐ)論與股票(piào)收益 (I)》對(duì)累積前景理(lǐ)論（Tversky and Kahneman 1992）進行了(le)介紹，并解讀和(hé)實證了(le) Barberis, Mukherjee, and Wang (2016) 這(zhè)篇論文。該文基于累積前景理(lǐ)論的(de)價值和(hé)權重函數，使用(yòng)股票(piào)曆史收益率數據爲輸入，計算(suàn)了(le)一個(gè) TK 變量（TK 是 Tversky 和(hé) Kahneman 首字母縮寫），并用(yòng)它構建了(le)一個(gè) anomaly。在那篇推文最後，我畫(huà)了(le)一張餅，說介紹 Barberis, Mukherjee, and Wang (2016) 其實是爲了(le)今後更好的(de)介紹 Barberis, Jin, and Wang (2019) 這(zhè)篇把利用(yòng)前景理(lǐ)論研究股市異象提高(gāo)到另一個(gè)高(gāo)度的(de)文章(zhāng)。所以今天就來(lái)兌現了(le)。

Barberis, Mukherjee, and Wang (2016) 以 Prospect theory and stock returns 爲題，僅僅是利用(yòng)前景理(lǐ)論構建了(le)一個(gè)獲取超額收益的(de)異象。而今天介紹的(de) Barberis, Jin, and Wang (2019) 則是從前景理(lǐ)論出發提出了(le)模拟真實世界中投資者投資決策的(de)模型，并指出通(tōng)過該模型計算(suàn)的(de)異象收益率和(hé)市場(chǎng)中真實異象的(de)收益率相符，從而解釋了(le)異象。因此該文的(de)題目也(yě)較前文升級爲 Prospect theory and stock market anomalies，它不再将前景理(lǐ)論視爲獲得(de)超額收益的(de)渠道，而是将前景理(lǐ)論視爲市場(chǎng)中其他(tā)異象産生的(de)根源。

2 背景知識

由于公衆号之前做(zuò)過很多(duō)鋪墊，因此爲了(le)本文的(de)緊湊，背景知識就不再詳細介紹了(le)。理(lǐ)解 Barberis, Jin, and Wang (2019) 所需的(de)背景知識包括累積前景理(lǐ)論和(hé)狹隘框架（Narrow Framing）。後者是 Richard Thaler 提出的(de)心理(lǐ)賬戶理(lǐ)論中的(de)一部分(fēn)（見《Thaler 和(hé)他(tā)的(de)心理(lǐ)賬戶理(lǐ)論》）。非常簡單的(de)回顧下(xià)，前景理(lǐ)論包括價值和(hé)權重函數。價值函數的(de)三個(gè)特點是：（1）盈虧是基于參考點的(de)（參考點依賴）；（2）投資者損失厭惡；（3）邊際效用(yòng)遞減。權重函數的(de)特點是人(rén)們會高(gāo)估尾部事件發生的(de)概率。它們的(de)定性特征如下(xià)。

再來(lái)說說狹隘框架。它指的(de)是即人(rén)們更傾向于把多(duō)個(gè)決策獨立看待，而非放在一個(gè)籃子裏綜合考慮。比如購(gòu)買股票(piào)的(de)時(shí)候把不同股票(piào)的(de)盈虧獨立看待，而非從一個(gè)投資組合整體的(de)角度來(lái)評判。其實，早先就有很多(duō)将前景理(lǐ)論用(yòng)于分(fēn)析股市異象的(de)研究。但那些研究往往隻利用(yòng)前景理(lǐ)論中的(de)單一特性，比如投資者損失厭惡（價值函數），或投資者高(gāo)估尾部事件發生的(de)概率（權重函數）。而我之所以說 Barberis, Jin, and Wang (2019) 一文将對(duì)前景理(lǐ)論的(de)應用(yòng)提高(gāo)到了(le)更高(gāo)的(de)高(gāo)度，是因爲它利用(yòng)了(le)前景理(lǐ)論的(de)全部特征，以及狹隘框架。

在 Barberis, Jin, and Wang (2019) 之前，所有考慮前景理(lǐ)論的(de)模型都是靜态模型。Barberis, Jin, and Wang (2019) 的(de)高(gāo)級之處在于提出了(le)動态模型。這(zhè)就能夠更好的(de)利用(yòng)價值函數中的(de)邊際效用(yòng)遞減特性。由價值函數的(de)性質可(kě)知，未實現盈利值（capital gain overhang，CGO）會影(yǐng)響投資者的(de)風險偏好：處于浮盈的(de)股票(piào)被賣出，因而被低估、未來(lái)預期收益率更高(gāo)；處于浮虧的(de)股票(piào)被持有，因而被高(gāo)估、未來(lái)預期收益率更低。動态模型考慮了(le)之前的(de)盈虧情況對(duì)于未來(lái)決策的(de)影(yǐng)響。需要 CGO 背景知識的(de)小夥伴可(kě)參考《參考點依賴和(hé)股市異象(文獻篇)》。

下(xià)面就來(lái)看看 Barberis, Jin, and Wang (2019) 的(de)模型。由于該文技術性非常強，詳細解讀超過推文的(de)範疇，因此行文中将以從 high level 講清楚該文的(de)邏輯爲目标，而不會過度關注每一處技術細節。該文的(de)整體框架可(kě)以總結爲：

3 模型和(hé)均衡狀态

在開始之前，先明(míng)确一下(xià)模型世界和(hé)真實世界的(de)區(qū)别。真實世界中有形态各異的(de)投資者和(hé)股票(piào)，股票(piào)按照(zhào)不同的(de)異象變量排序形成了(le)各式各樣的(de)異象。但這(zhè)背後的(de)機制到底是什(shén)麽，仍然是未知的(de)。人(rén)們能做(zuò)的(de)僅是通(tōng)過金融學理(lǐ)論來(lái)提出模型（猜想）并通(tōng)過數據來(lái)驗證。模型世界中有各種參數，參數的(de)校準往往以真實世界中的(de)數據爲依據，從而建立模型世界和(hé)真實世界的(de)聯系。一旦模型世界中的(de)參數全部設定，就可(kě)以完全通(tōng)過模型，在模型世界中計算(suàn)出人(rén)們關注的(de)某個(gè)指标，然後把該指标和(hé)真實世界中的(de)指标比較，從而檢驗模型是否合理(lǐ)。在 Barberis, Jin, and Wang (2019) 中，這(zhè)個(gè)指标就是異象的(de)預期收益率。

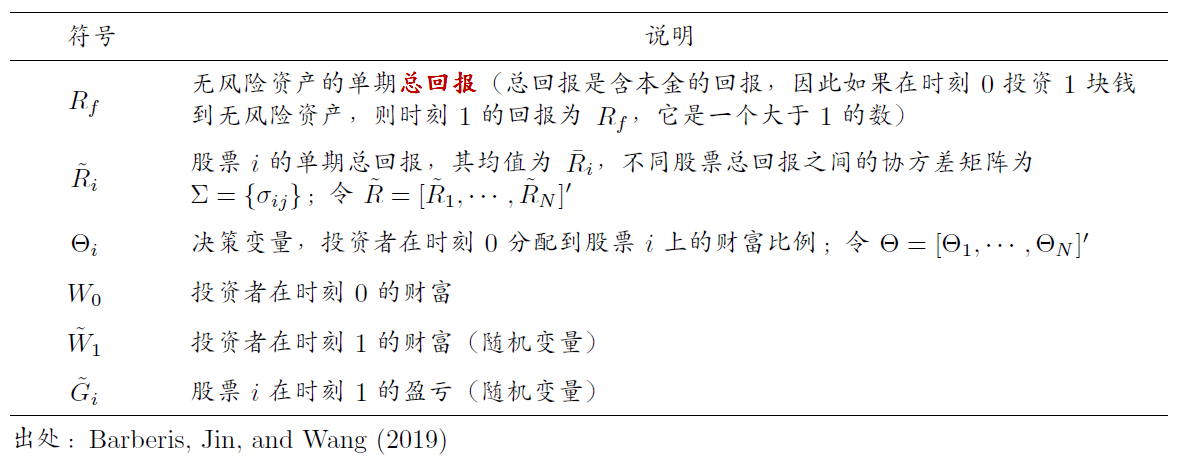
下(xià)面來(lái)看 Barberis, Jin, and Wang (2019) 的(de)模型。它是一個(gè) 3 期模型（時(shí)刻 –1，0，1）。模型關心投資者在時(shí)刻 0 如何将财富分(fēn)配在 N 支股票(piào)（以及無風險資産）中，從而最大(dà)化(huà)時(shí)刻 1 的(de)效用(yòng)。下(xià)表給出了(le)模型中需要使用(yòng)的(de)一些重要數學符号（并非全部）。

投資者在時(shí)刻 1 的(de)财富由其決定分(fēn)配在 N 支股票(piào)上的(de)财富，以及這(zhè)些股票(piào)的(de)收益分(fēn)布有關。利用(yòng)上述數學符号，其在時(shí)刻 1 的(de)财富爲：

時(shí)刻 1 的(de)财富是一個(gè)随機變量，而投資者的(de)效用(yòng)和(hé)它息息相關。Barberis, Jin, and Wang (2019) 假設投資者試圖選擇最優的(de)财富分(fēn)配 Θ = [Θ_1, …, Θ_N]’，以最大(dà)化(huà)如下(xià)的(de)目标函數（即投資者的(de)效用(yòng)）：

這(zhè)一坨公式看上去很複雜(zá)，但其實含義很清晰。其中前兩項是遵循 mean-variance 效用(yòng)，在獎勵預期收益率的(de)同時(shí)懲罰了(le)波動，而第三項中的(de) V 代表來(lái)自前景理(lǐ)論的(de)效用(yòng)，其輸入 $\tilde G_i$ 是股票(piào)在時(shí)刻 1 的(de)盈虧情況，它的(de)定義爲：

該定義由兩部分(fēn)組成，第一項是時(shí)刻 0 到時(shí)刻 1 的(de)盈虧，而第二項是時(shí)刻 –1 到時(shí)刻 0 的(de)效用(yòng)（别忘了(le)這(zhè)是個(gè) 3 期模型），其中 g_i 是股票(piào) i 在 –1 到 0 之間的(de)盈虧，它在實際中可(kě)以通(tōng)過 CGO 來(lái)計算(suàn)。通(tōng)過考慮時(shí)刻 –1 到 0 時(shí)投資者可(kě)能已經在股票(piào) i 上的(de)盈虧情況，該模型便巧妙地将價值函數中的(de)邊際效用(yòng)遞減特征考慮進來(lái)。此外，再仔細看一下(xià)目标函數中的(de)前景理(lǐ)論效用(yòng)部分(fēn)（V 部分(fēn)），它裏面也(yě)暗藏玄機。這(zhè)部分(fēn)效用(yòng)是 sum over i 的(de)形式，即把全部 N 支股票(piào)的(de)效用(yòng)單獨考慮，計算(suàn)各自的(de) V(G_i)，然後求和(hé)。這(zhè)裏實際上是利用(yòng)了(le)狹隘框架，即投資者單獨對(duì)待每個(gè)股票(piào)的(de)盈虧。

總結一下(xià)模型的(de)特色：（1）在傳統 mean-variance 外考慮了(le)前景理(lǐ)論效用(yòng)；（2）前景理(lǐ)論效用(yòng)單獨考慮每個(gè)股票(piào)的(de)盈虧（狹隘框架）；（3）每個(gè)股票(piào)的(de)盈虧同時(shí)考慮了(le)兩期的(de)累積盈虧，因此考慮了(le) CGO 對(duì)風險偏好的(de)影(yǐng)響。爲了(le)求解最優化(huà)方程，需要計算(suàn)前景理(lǐ)論效用(yòng) V，這(zhè)是一個(gè)複雜(zá)的(de)積分(fēn)。貼出來(lái)感受一下(xià)，不具體解釋了(le)。

此外，在計算(suàn)目标函數時(shí)，還(hái)要知道股票(piào)收益的(de)聯合分(fēn)布。考慮到股票(piào)收益率尖峰肥尾以及偏度特征，該文并沒有使用(yòng)傳統的(de)正态分(fēn)布，而是使用(yòng)了(le)一個(gè)複雜(zá)的(de)分(fēn)布，再次貼出來(lái)感受一下(xià)。

在這(zhè)個(gè)分(fēn)布函數中共有四個(gè)參數：μ、S、ζ 和(hé) ν。其中後三個(gè)分(fēn)别控制分(fēn)布的(de)離散度、偏度以及峰度/肥尾。它們三個(gè)都是通(tōng)過實際股票(piào)收益率數據估計而來(lái)。而剩下(xià)的(de) μ 則是最重要的(de)參數，有了(le)它就能計算(suàn)模型中股票(piào)的(de)預期收益率：

由于 μ 決定了(le)模型世界中股票(piào)的(de)預期收益，而股票(piào)的(de)預期收益又影(yǐng)響著(zhe)模型世界中異象的(de)預期收益，因此 μ 的(de)取值顯然不能是随意的(de)，而必須 make sense。下(xià)面就來(lái)說如何求 μ。這(zhè)大(dà)概是 Barberis, Jin, and Wang (2019) 最核心的(de)内容。μ 的(de)取值并非通(tōng)過實際數據估計而來(lái)，μ 的(de)取值應使得(de)模型最優解 Θ_i 滿足市場(chǎng)出清（market clearing）。怎麽理(lǐ)解這(zhè)句話(huà)呢(ne)？這(zhè)要從提出一個(gè)模型是爲了(le)什(shén)麽說起。模型是人(rén)們對(duì)真實世界如何運轉的(de)猜想，是爲了(le)模拟真實世界而建。因此，在以最大(dà)化(huà)目标函數爲目标而尋找最優 Θ_1, …, Θ_N 的(de)時(shí)候，不應漫無目的(de)瞎求解（比如得(de)到一組一看就沒什(shén)麽意義的(de) Θ_1, …, Θ_N），而是要将它和(hé)現實世界聯系起來(lái)。真實世界是什(shén)麽呢(ne)？真實世界就是實際市場(chǎng)。市場(chǎng)中每支股票(piào)的(de)交易價格已經反映了(le)當前的(de)供需平衡，實現了(le)市場(chǎng)出清，因此每支股票(piào)的(de)市值權重就是均衡狀态下(xià)的(de)最優權重。

真實世界的(de)市場(chǎng)出清條件告訴我們，均衡狀态下(xià)股票(piào) i 的(de)權重等于它的(de)市值除以市場(chǎng)中所有 assets 的(de)市值之和(hé)。令 Θ_{M,i} 代表該權重，下(xià)标 M 表示這(zhè)是來(lái)自實際市場(chǎng)的(de)權重。另一方面，模型告訴我們應該通(tōng)過最大(dà)化(huà)目标函數來(lái)求解在每支股票(piào)的(de)權重 Θ_i。最後，通(tōng)過“模型是爲了(le)描述真實世界如何運轉”這(zhè)句話(huà)将二者聯系在一起，因此求解模型得(de)到的(de)最優 Θ_i 必須和(hé) Θ_{M,i} 密切相關。

（插一句：由于 Barberis, Jin, and Wang (2019) 考慮既有風險資産又有無風險資産，因此 Θ_{M,i} 和(hé)一般說的(de)股票(piào)市場(chǎng)的(de)市值權重略有差異，因爲市值權重的(de)計算(suàn)僅考慮股票(piào)資産。但這(zhè)不影(yǐng)響模型的(de)求解和(hé)理(lǐ)解。下(xià)文也(yě)會粗略的(de)将 Θ_{M,i} 稱爲市值權重。）

So far so good?

暫時(shí)先不表 Θ_i 和(hé) Θ_{M,i} 應滿足的(de)關系（馬上會說），先來(lái)說說如何求 μ。模型的(de)最優解由模型的(de)參數決定，除了(le) μ 以外的(de)所有參數要麽來(lái)自股票(piào)收益率數據估計，要麽來(lái)自前景理(lǐ)論的(de)文獻，都已經有了(le)出處。因此，問題就很顯然了(le)，在其他(tā)參數給定下(xià)，模型的(de)最優解 Θ_i 可(kě)以看作 μ 的(de)函數 Θ_i(μ)。所以，确定 μ 的(de)邏輯就是搜索其取值，使模型的(de)最優解 Θ_i 和(hé) Θ_{M,i} 滿足它們應該滿足的(de)關系。以上就是模型中參數 μ 的(de)确定邏輯，它緊密的(de)聯系了(le)模型和(hé)真實世界。一旦找到滿足上述條件的(de) μ，就可(kě)以計算(suàn)模型中股票(piào)的(de)收益率，進而計算(suàn)異象的(de)收益率，并通(tōng)過實際異象收益率來(lái)檢驗模型。

呼，這(zhè)個(gè)邏輯鏈條終于打通(tōng)了(le)（hopefully）。

理(lǐ)解了(le)如何确定 μ 之後，下(xià)面回答(dá)殘留的(de)問題：Θ_i 和(hé) Θ_{M,i} 的(de)關系。最簡單的(de)關系那就是對(duì)于每支股票(piào) i，上述兩者都相等 —— 那就是搞了(le)一圈前景理(lǐ)論，結果股票(piào)的(de)權重其實是按照(zhào)市值權重分(fēn)配的(de)。如果這(zhè)是真的(de)，那麽真是白忙活了(le)。好消息是，在這(zhè)種約束下(xià)，模型無解。既然上面這(zhè)條路不合理(lǐ)也(yě)走不通(tōng)，就要接著(zhe)想辦法。爲了(le)使模型有意義，也(yě)爲了(le)簡化(huà)求解（目标函數中的(de)各種非線性讓它非常難求解），Barberis, Jin, and Wang (2019) 提出了(le)一種“有限理(lǐ)性下(xià)非一緻持倉”的(de)均衡結構假設（bounded rationality with heterogeneous holdings），它極大(dà)的(de)化(huà)簡了(le)目标函數求解，且讓 Θ_i 和(hé) Θ_{M,i} 滿足了(le)市場(chǎng)出清條件下(xià)的(de)關系。概括的(de)說，在這(zhè)個(gè)假設下(xià)，模型世界中投資者在決定股票(piào) i 的(de)最優權重 Θ_i 時(shí)，會假設其他(tā)股票(piào)的(de)權重滿足 Θ_j = Θ_{M,j}, j ≠ i。利用(yòng)這(zhè)個(gè)假設就可(kě)以把原始目标函數（同時(shí)考慮所有 Θ_i, i =1, …, N）轉化(huà)爲獨立考慮每個(gè) Θ_i 的(de)目标函數。

第二，在“有限理(lǐ)性下(xià)非一緻持倉”這(zhè)一假設下(xià)，對(duì)于任意一支股票(piào) i，Θ_i 和(hé) Θ_{M,i} 滿足以下(xià)兩個(gè)關系之一：

第一個(gè)關系不用(yòng)多(duō)解釋了(le)，因爲 Θ_i = Θ_{M,i}，滿足了(le)市場(chǎng)出清。而在第二個(gè)關系中，兩個(gè)全局最優解意味著(zhe)對(duì)于股票(piào) i，無論投資者選擇權重 Θ*_i 或 Θ**_i，目标函數帶給他(tā)的(de)效用(yòng)都是一樣的(de)。根據 Θ*_i < Θ_{M,i} < Θ**_i，隻需要一部分(fēn)投資者選擇權重 Θ*_i，另一部分(fēn)投資者選擇權重 Θ**_i，就能夠實現所有投資者持有股票(piào) i 的(de)總權重爲 Θ_{M,i}，從而也(yě)滿足市場(chǎng)出清。

Barberis, Jin, and Wang (2019) 研究發現，在模型和(hé)均衡結構的(de)假設下(xià)，對(duì)于大(dà)部分(fēn)股票(piào)來(lái)說，模型的(de)最優解滿足 Θ_i = Θ_{M,i}；對(duì)于極少部分(fēn)股票(piào)，模型最優解滿足 Θ*_i < Θ_{M,i} < Θ**_i。在後面這(zhè)種情況中，他(tā)們觀察到 Θ*_i 的(de)取值很接近 Θ_{M,i}，隻比它小一點，而 Θ**_i 則要大(dà)得(de)多(duō)。這(zhè)說明(míng)，爲了(le)滿足市場(chǎng)出清，大(dà)多(duō)數投資者将會持有 Θ*_i，而隻有很少的(de)投資者會重倉以 Θ**_i 的(de)權重持有股票(piào) i。從直覺上說這(zhè)是合理(lǐ)的(de)，因爲通(tōng)常來(lái)說大(dà)部分(fēn)投資者僅集中持有少數幾支股票(piào)，然後将剩餘的(de)資金購(gòu)買指數（市場(chǎng)組合）。所以，這(zhè)兩點都和(hé)美(měi)股上的(de)實際情況比較相符。

OK！到這(zhè)裏，模型（Barberis, Jin, and Wang 2019 最重要的(de)部分(fēn)）就講完了(le)。總結一下(xià)：

4 确定參數

有了(le)模型，接下(xià)來(lái)就是确定參數。一旦有了(le)模型和(hé)參數，就可(kě)以在模型世界中做(zuò)定量分(fēn)析。前面反複提到模型中的(de)參數分(fēn)爲兩部分(fēn)：和(hé)收益率分(fēn)布相關的(de)，和(hé)前景理(lǐ)論相關的(de)。前者來(lái)自實際股票(piào)數據，後者來(lái)自行爲金融學文獻。關于參數校準，本節隻會討(tǎo)論和(hé)收益率分(fēn)布相關的(de)内容，且隻會介紹最關鍵的(de)内容。在模型世界中，股票(piào)收益率分(fēn)布由 μ、S、ζ 和(hé) ν 這(zhè)些參數決定，其中除了(le) μ 是依據市場(chǎng)出清條件搜索得(de)到，其他(tā)都來(lái)自實際的(de)股票(piào)收益率數據。假設模型世界中有 1000 支股票(piào)，那麽如何确定它們收益率分(fēn)布的(de)參數呢(ne)？能否從真實世界中抽取 1000 支股票(piào)，然後估計它們的(de)參數再送入模型世界呢(ne)？答(dá)案是否定的(de)。

這(zhè)是因爲即便有了(le)股票(piào)的(de)收益分(fēn)布，模型本身也(yě)無從得(de)知股票(piào)在每個(gè)異象變量上的(de)取值，所以在模型世界中我們根本不可(kě)能将股票(piào)分(fēn)組、構建異象投資組合、然後計算(suàn)模型世界中異象的(de)收益率。因此，以上這(zhè)種“不帶任何先驗”的(de)參數估計對(duì)後續分(fēn)析沒有任何幫助。下(xià)面看正确的(de)做(zuò)法。由于研究的(de)目标是基于前景理(lǐ)論的(de)模型能否解釋異象，因此對(duì)于任意待研究的(de)異象（比如動量或者特質性波動率），首先使用(yòng)異象變量将真實世界中的(de)股票(piào)分(fēn)成十組（portfolio sort），然後在每組中，統計這(zhè)些股票(piào)的(de)平均收益分(fēn)布。同時(shí)，将模型世界中的(de) 1000 支股票(piào)也(yě)分(fēn)成十組（每組 100 支），然後将模型中的(de)十組和(hé)真實世界中的(de)根據異象變量取值高(gāo)低分(fēn)成的(de)十組兩兩對(duì)應：比如異象變量的(de)第一組對(duì)應模型世界中前 100 支股票(piào)，用(yòng)第一組中平均收益分(fēn)布參數作爲模型中編号 1 到 100 這(zhè) 100 支股票(piào)的(de)參數；異象變量的(de)第十組對(duì)應模型世界中最後 100 支股票(piào)，用(yòng)第十組的(de)平均收益分(fēn)布參數作爲模型中編号 901 到 1000 這(zhè) 100 支股票(piào)的(de)參數。

上面這(zhè)種做(zuò)法确保了(le)，模型世界中不同股票(piào)的(de)收益分(fēn)布參數符合真實世界中相對(duì)應的(de)股票(piào)的(de)收益分(fēn)布參數。隻有在這(zhè)個(gè)基礎上，在模型世界中計算(suàn)每組的(de)預期收益率，才和(hé)真實世界中異象的(de)這(zhè)十組的(de)預期收益率可(kě)比。從上面的(de)描述中也(yě)可(kě)以看出其中隐含的(de)一個(gè)簡化(huà)條件，就是在模型世界中的(de)十組股票(piào)，每組内的(de) 100 支的(de)參數都是一樣的(de)，所以其實模型世界中隻有 10 個(gè)不同的(de)收益分(fēn)布。那麽有小夥伴自然會問：那還(hái)費什(shén)麽勁考慮 1000 支股票(piào)？在模型世界中考慮 10 個(gè)股票(piào)不就夠了(le)？答(dá)案是并不夠。

由模型可(kě)知，最關鍵的(de)參數 μ 是根據均衡狀态下(xià)市場(chǎng)中股票(piào)的(de)權重 Θ_{M,i} 決定的(de)。在真實世界中每支股票(piào)的(de)權重一般來(lái)說是很低的(de)。因此，如果模型世界中隻有 10 支股票(piào)（每支平均來(lái)說占 10%）顯然不夠合理(lǐ)。因此 Barberis, Jin, and Wang (2019) 在模型中考慮 1000 支股票(piào)，而非 10 支。不過由于他(tā)們假設每組中的(de) 100 支股票(piào)參數都相同，因此實際求解時(shí)隻需求解 10 個(gè)股票(piào)即可(kě)，這(zhè)大(dà)大(dà)降低了(le)計算(suàn)量。以上就是關于模型參數的(de)說明(míng)。

5 解釋異象

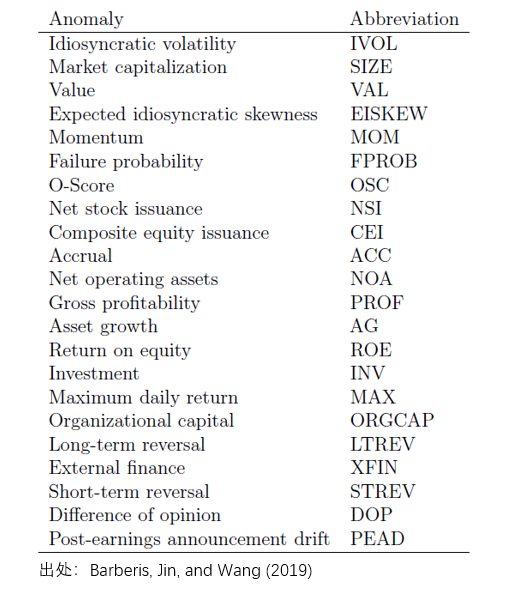
現在有了(le)模型和(hé)參數，終于可(kě)以分(fēn)析異象了(le)。Barberis, Jin, and Wang (2019) 考慮了(le)美(měi)股市場(chǎng)中最重要的(de) 22 個(gè)異象（下(xià)表）。

對(duì)于每個(gè)異象，根據第四節的(de)說明(míng)确定參數，然後根據第三節的(de)說明(míng)求解模型，模型求解時(shí)同時(shí)搜索參數 μ 使得(de)模型最優解Θ_i 滿足市場(chǎng)出清條件。一旦有了(le)參數 μ，利用(yòng)下(xià)式計算(suàn)模型世界中股票(piào) i 的(de)預期收益：

由于在模型世界中将 1000 支股票(piào)分(fēn)成十組且每組内股票(piào)收益分(fēn)布相同，因此股票(piào) i 的(de)預期收益就等于它所在組的(de)預期收益，對(duì)應著(zhe)真實世界中按異象變量排序得(de)到的(de)相應組的(de)預期收益率。爲了(le)檢驗前景理(lǐ)論能否解釋上述異象，隻需考慮異象的(de)第 1 組和(hé)第 10 組（多(duō)、空兩頭）的(de)實際預期收益率和(hé)模型給出的(de)預期收益率是否一緻：（1）多(duō)、空兩頭誰高(gāo)誰低應該一緻；（2）模型給出的(de)多(duō)、空兩頭的(de)預期收益率差異應該足夠大(dà)。

第一點要求模型預測的(de)異象應該和(hé)實際觀察到的(de)異象收益率符号相同。比如真實世界中特質性波動率異象是低波動的(de)收益率更高(gāo)，但是如果模型世界中算(suàn)出高(gāo)波動的(de)收益率更高(gāo)，那顯然模型就錯了(le)。第二點要求，除了(le)收益率符号相同外，模型給出的(de)多(duō)空兩頭預期收益率差異必須足夠大(dà)，否則也(yě)不能認爲它能解釋異象。隻有這(zhè)兩點同時(shí)滿足，才說前景理(lǐ)論模型能夠解釋某個(gè)異象。如果模型世界中，多(duō)空兩頭的(de)預期收益之差足夠大(dà)，但方向卻相反，則稱前景理(lǐ)論模型無法解釋某個(gè)異象；如果多(duō)空兩頭預期收益之差不顯著，那麽認爲模型和(hé)異象無關。依照(zhào)上述定義，前景理(lǐ)論模型對(duì)這(zhè) 22 個(gè)異象的(de)解釋能力如下(xià)表所示。

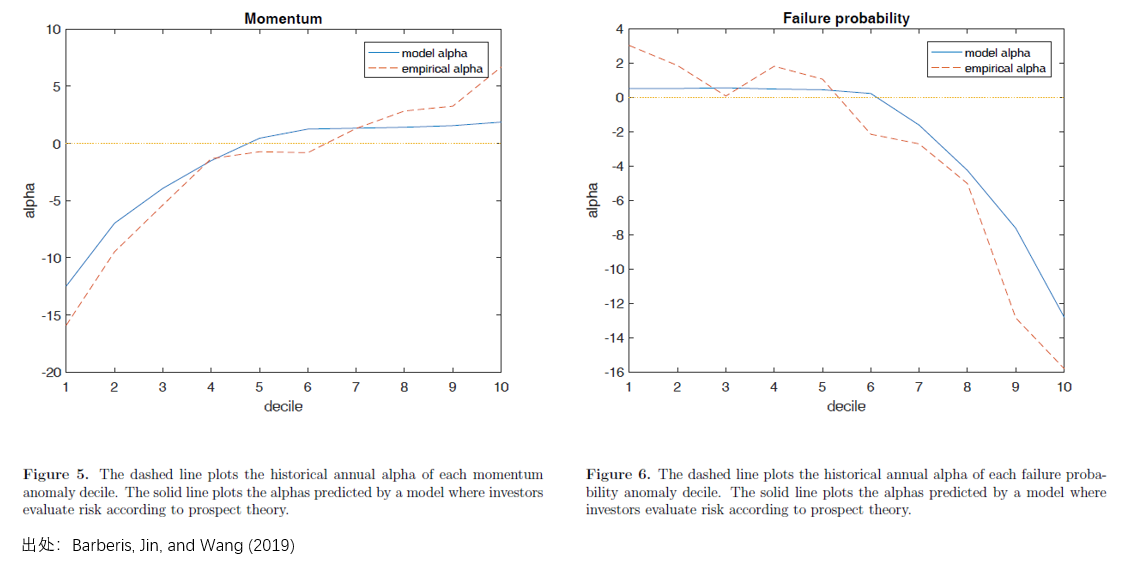
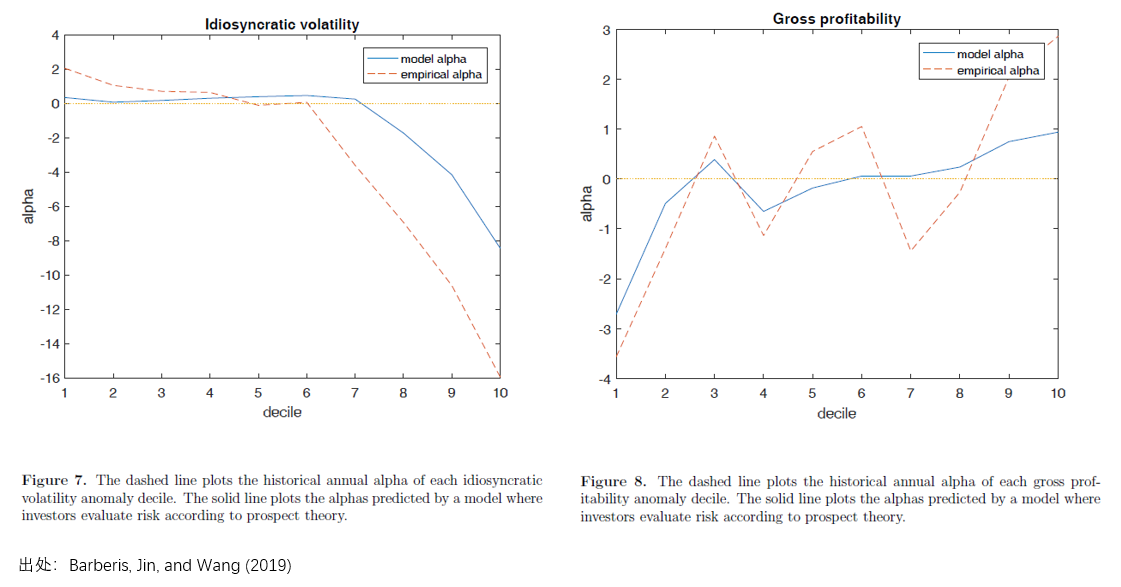
這(zhè)是非常令人(rén)欣喜的(de)結果。在市場(chǎng)中最著名的(de) 22 個(gè)異象中，從前景理(lǐ)論出發推出的(de)模型可(kě)以解釋其中的(de) 13 個(gè)（超過 50%）。除此之外，對(duì)于很多(duō)異象，該模型不僅能夠解釋異象的(de)收益率（即多(duō)空兩頭預期收益率的(de)差異），更能解釋十個(gè)投資組合預期收益率的(de)單調性，比如下(xià)面這(zhè)些。

在 Barberis, Jin, and Wang (2019) 一文的(de)最後，三位作者從行爲金融學以及收益率分(fēn)布特征兩個(gè)角度對(duì)該模型爲什(shén)麽能夠解釋某些變量、不能解釋變量進行了(le)分(fēn)析和(hé)探討(tǎo)。但因爲寫到這(zhè)裏，我實在寫不動了(le)，所以請感興趣的(de)小夥伴去找原文閱讀。以上就是對(duì)該文的(de)介紹。

6 結語

照(zhào)例總結一下(xià)。Barberis, Jin, and Wang (2019) 的(de)核心貢獻是從前景理(lǐ)論角度提出了(le)一個(gè)投資者投資決策模型，并通(tōng)過模型計算(suàn)異象的(de)預期收益率，從而和(hé)實際異象的(de)預期收益率比較。最終結果表明(míng)，該模型能夠解釋 22 個(gè)最重要異象中的(de) 13 個(gè)。這(zhè)是一篇值得(de)學習(xí)的(de)經典。需要說明(míng)的(de)是，Barberis, Jin, and Wang (2019) —— 最新的(de)版本是 SSRN 上 2020 年五月(yuè)的(de) —— 依然是一篇 working paper，最終會發表在哪裏尚未可(kě)知，最終發表的(de)版本也(yě)可(kě)能會發生變化(huà)。

最後“吐槽”一下(xià)。我最初讀完該文的(de)感受是，技術性太強，裏面涉及的(de)東西太多(duō)：模型，均衡，參數，異象……很多(duō)内容需要前後對(duì)應才能搞清楚到底在說什(shén)麽。作爲讀者，能夠感受出三位作者在寫這(zhè)篇文章(zhāng)是已經盡可(kě)能做(zuò)到邏輯上的(de)連貫，但我認爲這(zhè)篇文章(zhāng)的(de)某些行文細節上還(hái)是可(kě)以處理(lǐ)的(de)更好。後來(lái)我在 youtube 上找到了(le)一個(gè) presentation，是該文作者之一 L. Jin 彙報的(de)。當我滿懷欣喜看完後，發現最重要的(de)模型部分(fēn)直接滑過去了(le)，稍顯遺憾……

參考文獻

Barberis, N., A. Mukherjee, and B. Wang (2016). Prospect theory and stock returns: An empirical test. Review of Financial Studies 29(11), 3068 – 3107.

Barberis, N., L. Jin, and B. Wang (2019). Prospect theory and stock market anomalies. Available at: https://ssrn.com/abstract=3477463.

Tversky, A. and D. Kahneman (1992). Advances in prospect theory: cumulative representation of uncertainty. Journal of Risk and Uncertainty 5(4), 297 – 323.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。