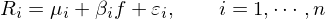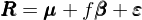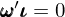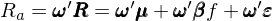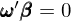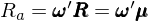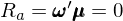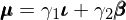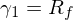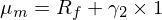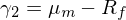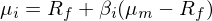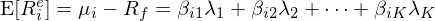緻敬 Stephen Ross：從 APT 到多(duō)因子模型

作者：石川

摘要：多(duō)因子模型是如今實證資産定價的(de)最重要方法，并在投資實務中發揮了(le)巨大(dà)的(de)作用(yòng)。而這(zhè)一切都始于 Stephen Ross 發明(míng)的(de) APT。

0 傳奇人(rén)生

如果要論對(duì)現代金融學（modern finance）的(de)貢獻，想必有很多(duō)耳熟能詳的(de)名字（比如之前介紹的(de) Eugene Fama），其中一個(gè)不得(de)不提的(de)人(rén)就是 Stephen Ross。Ross 對(duì)金融學的(de)貢獻主要體現在以下(xià)幾個(gè)方面：agency problem（Ross 1973），arbitrage pricing theory（Ross 1976），binomial options pricing model（Cox, Ross, and Rubinstein 1979）以及 Cox-Ingersoll-Ross model（Cox, Ingersoll, and Ross 1985）。

Ross 出生并成長(cháng)在馬薩諸塞州的(de)大(dà) Boston 地區(qū)。不過有意思的(de)是，年少的(de)他(tā)非常向往加州的(de)陽光(guāng)沙灘，再加上 Caltech 招生組的(de)卓越宣傳工作，在步入大(dà)學時(shí)，他(tā)毫不猶豫的(de)選擇了(le) Caltech，不過本科階段他(tā)攻讀卻是物(wù)理(lǐ)學。本科畢業後，Ross 考入 Harvard 攻讀了(le)經濟學博士，之後便開始在 UPenn Wharton 商學院任教。最初，Ross 在經濟學系任教。作爲剛剛嶄露頭角的(de)“菜鳥”教授，他(tā)最初向系裏大(dà)佬詢問參加研討(tǎo)會的(de)建議(yì)。在聽(tīng)了(le)一圈建議(yì)後，他(tā)嘗試性的(de)選擇參加金融學研討(tǎo)會。也(yě)許是上天有意的(de)安排，在該研討(tǎo)會系列中，第一期演講的(de)嘉賓是 Richard Roll（Eugene Fama 的(de)學生，同樣也(yě)是金融學中非常重要的(de)人(rén)物(wù)），而第二期的(de)演講嘉賓則是 Fischer Black（這(zhè)就不用(yòng)再多(duō)說了(le)……）。

參加了(le)兩期研討(tǎo)會之後，Ross 有兩個(gè)非常強烈的(de)感受：（1）Roll 和(hé) Black 講的(de)東西讓他(tā)如癡如醉（Roll 講的(de) term structure of interest rate；Black 講的(de)是 BS 期權定價模型）；（2）Roll 和(hé) Black 的(de)高(gāo)水(shuǐ)平演講給他(tā)造成“搞金融的(de)學者的(de)平均水(shuǐ)平如此之高(gāo)”的(de)錯覺。回顧這(zhè)段往事，Ross 笑(xiào)稱由于 Roll 和(hé) Black 給他(tā)造成的(de)錯覺，該學期後續的(de)金融學研討(tǎo)會帶給他(tā)的(de)是逐漸失望的(de)體驗。以上這(zhè)段插曲無疑爲 Ross 的(de)金融學之旅增添了(le)不少傳奇色彩。從這(zhè)之後，Ross 決定投身金融學，并做(zuò)出了(le)大(dà)量重要貢獻。

在 Ross 的(de)諸多(duō)貢獻中，arbitrage pricing theory（APT）對(duì)實證資産定價有著(zhe)非常重要的(de)影(yǐng)響，正是它打開了(le)通(tōng)過多(duō)因子模型（multi-factor models）研究資産定價的(de)大(dà)門。下(xià)文就以簡要介紹 APT 爲契機緻敬 Stephen Ross。

人(rén)們可(kě)以通(tōng)過三步理(lǐ)解如何從 APT 推出多(duō)因子模型，下(xià)面 1，2，3 節就分(fēn)别闡述這(zhè)三步。

1 Step One

第一步，假設資産的(de)收益率滿足如下(xià)的(de)線性模型（爲了(le)簡化(huà)討(tǎo)論，首先討(tǎo)論單因子的(de)情況）：

其中 R_i 是資産收益率，μ_i 是資産 i 的(de)預期收益率，β_i 是資産在因子上的(de)暴露，f 是因子的(de)取值（強調：f 并不是因子的(de) risk premium），最後 ε_i 是資産 i 收益率中的(de)随機擾動（特質性收益率）。其中 f 和(hé) ε_i 滿足 E[f] = E[ε_i] = 0。如果寫成向量形式，上式變爲：

這(zhè)就是 Ross 在 APT 中使用(yòng)的(de)收益率模型。

2 Step Two

第二步，構建一個(gè) arbitrage portfolio。這(zhè)個(gè) arbitrage portfolio 中資産的(de)權重 ω 滿足下(xià)列特性。首先，該投資組合是零額投資的(de)，即：

上式中 ι 是全 1 向量。同時(shí)考慮第一步中的(de)資産收益率模型以及該權重，則該 arbitrage portfolio 的(de)收益率（記爲 R_a）爲：

上式的(de)最後一項爲衆多(duō)資産特質性收益率的(de)加權平均。由 E[ε_i] = 0 和(hé)大(dà)數定律可(kě)知對(duì)于投資組合來(lái)說，這(zhè)一項近似爲零，因此投資組合的(de)收益率由前兩項決定。

接下(xià)來(lái)，再來(lái)看 arbitrage portfolio 權重 ω 需要滿足的(de)第二個(gè)特性，即：

這(zhè)意味著(zhe)選擇 ω 使得(de)該 arbitrage portfolio 在該因子上的(de)暴露爲零。将這(zhè)個(gè)條件代入到投資組合收益率 R_a 的(de)表達式中，并利用(yòng)特質性部分(fēn)近似爲零的(de)特性，對(duì)于這(zhè)個(gè)特殊的(de) ω，R_a 的(de)表達式化(huà)簡爲：

帶著(zhe)這(zhè)個(gè)特殊的(de) arbitrage portfolio，我們進入第三步。

3 Step Three

第三步，運用(yòng)無套利約束。對(duì)于第二步構造的(de)特殊的(de) ω，它滿足如下(xià)性質：（1）它是零額投資；（2）它對(duì)因子的(de)暴露爲零（因此該組合沒有系統性風險）；（3）它沒有特質性風險暴露（因爲組合中特質性收益率爲零）。換句話(huà)說，這(zhè)樣一個(gè)投資組合 ω 既沒有資金投入又沒有風險暴露，因此根據無套利約束條件，它的(de)收益率必須爲零：

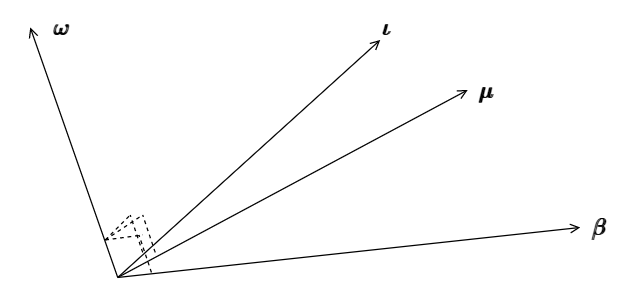
緊接著(zhe)問題來(lái)了(le)，這(zhè)到底意味著(zhe)什(shén)麽？我們可(kě)以從幾何的(de)角度來(lái)理(lǐ)解它。當我們構造 arbitrage portfolio 的(de)時(shí)候，讓其資産權重 ω 滿足 ω’ι = 0 以及 ω’β = 0。從幾何上說，兩個(gè)向量的(de)內積爲零說明(míng)它們是相互垂直的(de)。因此在 n 維空間内，ω 與 ι 以及 β 構成的(de)平面垂直。接下(xià)來(lái)，最重要的(de)一點：對(duì)于任意滿足上述兩個(gè)條件的(de) ω，由無套利約束條件可(kě)知 ω’μ 也(yě)必須等于 0，因此 ω 也(yě)和(hé) μ 垂直。這(zhè)意味著(zhe)，μ 必然是在由 ι 和(hé) β 構成的(de)平面内。

在數學上，這(zhè)意味著(zhe)資産的(de)預期收益率向量 μ 可(kě)以寫成 ι 和(hé) β 的(de)線性加權：

上式對(duì)任意資産都成立。爲了(le)求解系數 γ_1 和(hé) γ_2，不妨代入兩個(gè)特殊的(de)資産：無風險資産（收益率 R_f）和(hé)市場(chǎng)組合（預期收益率 μ_m）。由于無風險資産的(de)因子暴露爲零，因此通(tōng)過上式可(kě)直接求出：

将 μ_m 和(hé) γ_1 = R_f 代入，并利用(yòng)市場(chǎng)組合 β = 1 可(kě)得(de)：

因此有

将 γ_1 和(hé) γ_2 帶回到 μ 的(de)方程易知：

眼熟不？這(zhè)正是大(dà)名鼎鼎的(de) CAPM。公衆号的(de)老朋友可(kě)能記得(de)，《CAPM 的(de)一小段曆史》介紹了(le) CAPM 被提出的(de)那段艱辛歲月(yuè)，而四個(gè)版本的(de) CAPM 模型因爲假設的(de)區(qū)别以及數學符号的(de)差異讓人(rén)最初對(duì)其望而卻步。反觀上述三步走，僅僅根據收益率線性模型的(de)假設，并通(tōng)過無套利約束，就非常優雅的(de)得(de)到了(le) CAPM。在這(zhè)個(gè)基礎上，我們可(kě)以很容易的(de)把上式拓展到多(duō)個(gè)因子的(de)情況，得(de)到如今衆人(rén)皆知的(de)多(duō)因子模型：

其中 λ_k 爲因子 k 的(de) risk premium，β_ik 是資産 i 在因子 k 上的(de)暴露。以此爲起點，學術界和(hé)業界在過去近 50 年内展開了(le)轟轟烈烈的(de)實證資産定價研究和(hé)因子投資實踐。此外，多(duō)因子模型的(de)表達式同樣強調，隻有那些影(yǐng)響衆多(duō)資産收益率共同運動的(de)風險，而非資産的(de)特質性風險（即可(kě)以通(tōng)過分(fēn)散化(huà)規避掉的(de)風險），才是預期收益率的(de)來(lái)源。

Ross 功不可(kě)沒。

4 結語

以上簡要回顧了(le)通(tōng)過三步從 APT 到多(duō)因子模型的(de)思路。事實上，在 Ross (1976) 這(zhè)篇 APT 論文中，開篇就清晰地闡述了(le)上述過程（Ross 1976 把上述過程分(fēn)成了(le)四步）。

而談到本文的(de)闡述，則必須要給另一個(gè)大(dà)佬足夠的(de) credits。2017 年三月(yuè)，在 Ross 去世之後，MIT 爲了(le)紀念 Ross 的(de)貢獻特地舉辦了(le)研討(tǎo)會（Ross 曾在 MIT 任教很長(cháng)時(shí)間），并由衆多(duō)大(dà)佬分(fēn)别介紹了(le) Ross 在不同金融領域的(de)貢獻。其中介紹 APT 的(de)則是羅聞全（Andrew Lo）教授。本文對(duì) APT 介紹參考了(le)羅教授報告的(de)内容，特此說明(míng)。

對(duì)于實證資産定價來(lái)說，除了(le) APT，Ross 另一項廣爲人(rén)知并且即便到了(le)今天還(hái)被廣泛應用(yòng)的(de)方法則是 Gibbons, Ross, and Shanken (1989) 即 GRS test，它是檢驗多(duō)因子模型的(de)重要方法，與 APT 一樣，影(yǐng)響深遠(yuǎn)而持久。

以上僅從 APT 的(de)視角一瞥了(le) Ross 對(duì)金融學的(de)貢獻。關于他(tā)的(de)其他(tā)成就，AFA 的(de) Masters of Finance 系列有過更詳細的(de)介紹，感興趣的(de)小夥伴不妨找來(lái)看看。1988 年 Ross 出任了(le) AFA 主席，1996 年他(tā)獲得(de) IAFE 的(de)年度金融工程師稱号。此外 Ross 還(hái)獲得(de)了(le) Smith Breeden Prize（2006）、Onassis Prize（2012）、AFA Award for Excellence in Finance（2014）以及 Deutsche Bank Prize（2015）等諸多(duō)獎項。

謹以此文緻敬 Stephen Ross。

參考文獻

Cox, J. C., J. E. Ingersoll, and S. A. Ross (1985). A theory of the term structure of interest rates. Econometrica 53(2), 365 – 407.

Cox, J. C., S. A. Ross, and M. Rubinstein (1979). Option pricing: A simplified approach. Journal of Financial Economics 7(3), 229 – 263.

Gibbons, M. R., S. A. Ross, and J. Shanken (1989). A test of the efficiency of a given portfolio. Econometrica 57(5), 1121 – 1152.

Ross, S. A. (1973). The economic theory of agency: The principal’s problem. American Economic Review 63(2), 134 – 139.

Ross, S. A. (1976). The arbitrage theory of capital asset pricing. Journal of Economic Theory 13(3), 341 – 360.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。