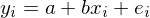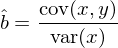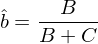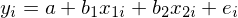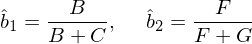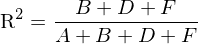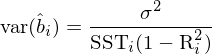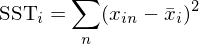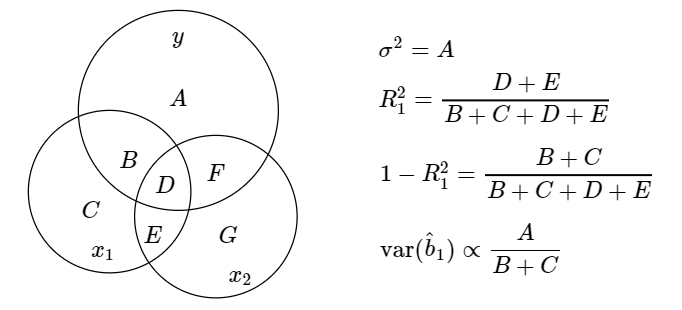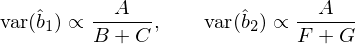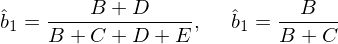用(yòng) Venn Diagram 理(lǐ)解多(duō)元線性回歸的(de) OLS 估計

作者：石川

摘要：Venn diagram 爲理(lǐ)解多(duō)元回歸模型的(de) OLS 估計提供了(le)直觀思路。通(tōng)過它，人(rén)們很容易搞懂(dǒng)共線性、遺漏變量造成的(de)問題，并直觀的(de)感受 R-squared、回歸系數估計以及其誤差的(de)高(gāo)低。

1 引言

線性回歸模型以及其估計方法 OLS 在實證資産定價中發揮了(le)重要的(de)作用(yòng)。例如傳統 Fama-French 三因子時(shí)序回歸模型以及 Fama and MacBeth (1973) 截面回歸都是這(zhè)樣的(de)例子。相信各位小夥伴對(duì)此都不陌生。

今天這(zhè)篇小文将從一個(gè)非常直觀的(de)角度解釋多(duō)元線性回歸背後的(de)機制，并探討(tǎo)常見的(de)多(duō)重共線性以及遺漏變量将會對(duì)回歸系數估計造成何種影(yǐng)響。這(zhè)個(gè)直觀的(de)角度就是 Venn Diagram（韋恩圖）。必須強調的(de)是，Venn diagram 的(de)目的(de)是提供直觀理(lǐ)解，加深人(rén)們對(duì) OLS 估計機理(lǐ)的(de)認知。Venn Diagram 由英國數學家 John Venn 發明(míng)，用(yòng)于展示在不同的(de)事物(wù)群組（集合）之間的(de)數學或邏輯聯系。

A Venn diagram, also called primary diagram, set diagram or logic diagram, is a diagram that shows all possible logical relations between a finite collection of different sets.

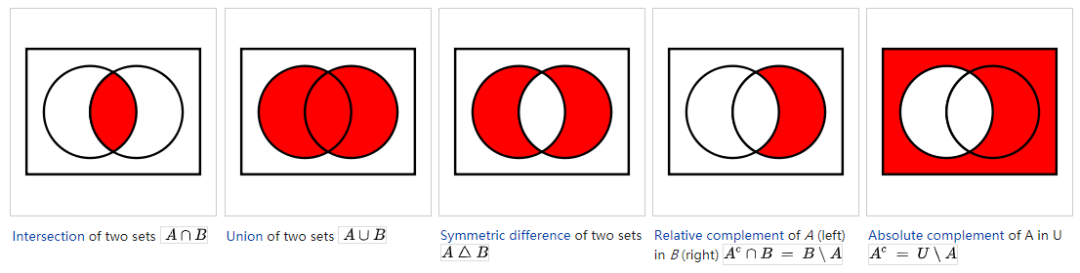
例如下(xià)面這(zhè)組圖就展示了(le)兩個(gè)集合之間的(de)不同關系（出處：wikipedia）：

那麽 Venn diagram 和(hé) OLS 又有什(shén)麽關系？将 Venn diagram 用(yòng)于解釋多(duō)元線性回歸可(kě)以追溯到 Cohen and Cohen (1975)，之後 Kennedy (1981, 2002)、Ip (2001) 等在其基礎上又有了(le)大(dà)量的(de)拓展。此外，邱嘉平教授的(de)《因果推斷實用(yòng)計量方法》一書(shū)對(duì) Venn diagram 也(yě)有涉及。下(xià)面就先來(lái)說說基本要素。

2 基本要素

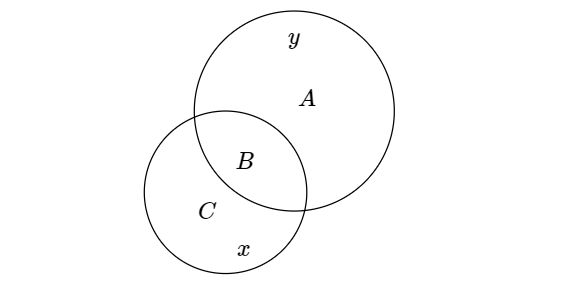
當使用(yòng) Venn diagram 研究回歸問題時(shí)，每個(gè)變量可(kě)被表示成一個(gè)圓圈，而圓圈的(de)面積則用(yòng)來(lái)表示每個(gè)變量的(de)方差 —— 面積越大(dà)表示方差越大(dà)；而兩個(gè)圓圈重疊的(de)部分(fēn)則表示兩變量相互關聯的(de)部分(fēn)，即協方差。以上就是研究的(de)基本要素。以下(xià)圖爲例，考慮解釋變量 x 和(hé)被解釋變量 y。兩個(gè)圓圈分(fēn)别表示它們各自的(de)方差，重疊的(de)部分(fēn) B 則表示它們共同運動的(de)部分(fēn)，即 x 和(hé) y 的(de)協方差。

依照(zhào)圖中信息，y 的(de)方差 var(y) 爲 A + B 的(de)面積；x 的(de)方差 var(x) 爲 B + C 的(de)面積；x 和(hé) y 的(de)協方差 cov(x, y) 爲 B 的(de)面積。帶著(zhe)這(zhè)些要素，馬上來(lái)看單一解釋變量的(de)情況。

3 單個(gè)解釋變量

假設 y 和(hé) x 滿足以下(xià)線性回歸模型：

通(tōng)過 OLS 對(duì)其進行估計可(kě)得(de)（這(zhè)裏我們隻關心 x_i 的(de)回歸系數 b 的(de)估計）：

對(duì)應上一節的(de) Venn diagram 中的(de)定義，馬上可(kě)以看出 b 的(de)估計爲 B 的(de)面積和(hé) B + C 面積之比：

結合 Venn diagram 和(hé) b 估計量的(de)定義可(kě)以總結出以下(xià)三點：

以上就是一元回歸的(de)直觀理(lǐ)解。

4 多(duō)元回歸

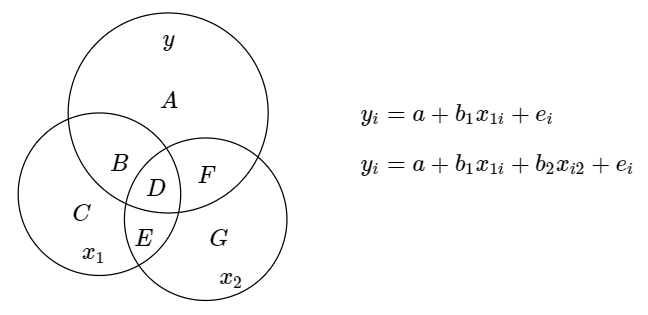
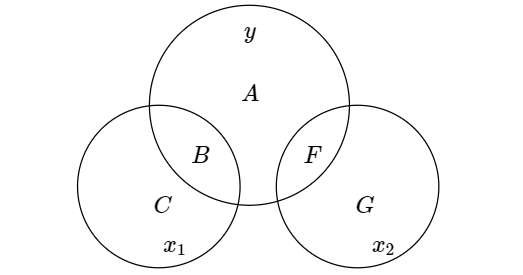
下(xià)面來(lái)看多(duō)元回歸的(de)情況。多(duō)元回歸要比一元回歸有（fu）趣（za）的(de)多(duō)。爲了(le)便于理(lǐ)解，考慮兩個(gè)不完全獨立的(de)解釋變量 x_1 和(hé) x_2，以及被解釋變量 y。它們之間的(de)關系滿足以下(xià)線性回歸模型：

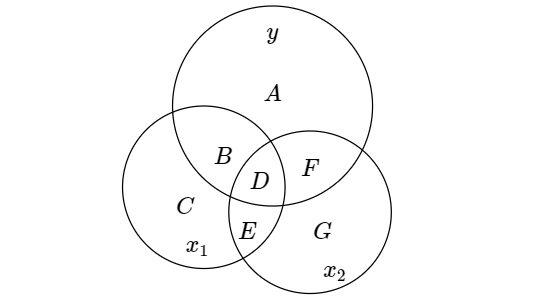
當使用(yòng) Venn diagram 時(shí)，它們的(de)關系如下(xià)圖所示。

從圖中可(kě)知，x_1 和(hé) y 相關聯的(de)部分(fēn)可(kě)通(tōng)過 B + D 的(de)面積表示，而 x_2 和(hé) y 相關聯的(de)部分(fēn)則可(kě)由 F + D 表示。而這(zhè)其中 D 是共有的(de)部分(fēn)，即 D 部分(fēn)表示的(de) y 的(de)波動是由 x_1 和(hé) x_2 共同驅動的(de)。那麽問題來(lái)了(le)，在 OLS 估計 b_1 和(hé) b_2 時(shí)，應該用(yòng)到 Venn diagram 中的(de)哪部分(fēn)信息？得(de)到的(de)估計又是否是無偏的(de)？考慮以下(xià)三個(gè)選項，你認爲哪個(gè)是正确的(de)？

怎麽樣？思考一下(xià)。如果你選擇了(le) 3，那麽恭喜你！1 和(hé) 2 之所以不對(duì)，恰恰是因爲 D 部分(fēn)表示的(de) y 的(de)波動是由 x_1 和(hé) x_2 共同驅動的(de)，因此難以分(fēn)清兩個(gè)解釋變量各自的(de)貢獻；D 又被稱爲被污染的(de)信息。此外，當僅使用(yòng) B 和(hé) F 分(fēn)别估計 b_1 和(hé) b_2 時(shí)，由于 B 和(hé) x_2 無關，F 和(hé) x_1 無關，因此得(de)到的(de) b_1 和(hé) b_2 的(de)估計也(yě)都是無偏的(de)。OLS 背後的(de)數學原理(lǐ)也(yě)恰恰保證了(le)這(zhè)一點。如果用(yòng) Venn diagram 圖中的(de)部分(fēn)表示，則 b_1 和(hé) b_2 的(de)估計量分(fēn)别爲：

除此之外，和(hé)一元回歸類似，在上圖中 A 的(de)部分(fēn)代表 y 中無法被 x_1 和(hé) x_2 解釋的(de)部分(fēn)，因此它是擾動項 e 的(de)方差。此外，通(tōng)過 Venn diagram 也(yě)可(kě)以方便的(de)看出可(kě)決系數 R-squared 的(de)定義，它是 B、D、F 三部分(fēn)面積之和(hé)與 A、B、D、F 四部分(fēn)面積之和(hé)之比：

有的(de)小夥伴可(kě)能已經注意到了(le)，雖然在估計回歸系數時(shí)舍棄了(le) D，但是在計算(suàn) R-squared 時(shí)卻沒有。這(zhè)是因爲 D 是兩個(gè)解釋變量共同解釋 y 的(de)部分(fēn)。雖然我們無法分(fēn)清每個(gè)變量貢獻了(le)多(duō)少，但它們作爲一個(gè)整體依然對(duì)解釋 y 的(de)波動有貢獻，因此在計算(suàn) R-squared 時(shí)應考慮 Venn diagram 中 D 的(de)面積。

回到我們關注的(de)問題 —— 實證資産定價，僅僅得(de)到回歸系數的(de)估計是不夠的(de)，很多(duō)時(shí)候都要知道估計的(de) standard error，才能進行檢驗。由 OLS 性質可(kě)知，對(duì)于回歸系數 b_i，其估計值的(de)方差可(kě)由下(xià)式決定：

式中的(de)分(fēn)子是模型中随機擾動項的(de)方差（實際中代入樣本方差即可(kě)，再對(duì)上式開根号就得(de)到 standard error）。R_i^2 爲用(yòng) x_i 對(duì)其他(tā)所有 x_j 回歸的(de)可(kě)決系數；R_i^2 越高(gāo)說明(míng) x_i 和(hé)其他(tā)解釋變量相關性越高(gāo)。最後，SST_i 是變量 x_i 的(de) total sample variation（不難看出它和(hé) x_i 的(de)方差就差一個(gè)系數）：

Var(\hat b_i) 的(de)表達式說明(míng)，當 x_i 自身的(de)波動越大(dà)且/或 x_i 和(hé)其他(tā)解釋變量的(de)相關性越低時(shí)，其估計誤差越小。

由于 Venn diagram 中的(de)面積表示方差或協方差，且結合前述 R-squared 的(de)定義，就可(kě)以通(tōng)過 Venn diagram 中的(de)元素清晰的(de)反映出 var(\hat b_i) 的(de)表達式。舉例來(lái)說，在本節考慮的(de)二元回歸模型中，x_1 的(de)回歸系數估計 \hat b_1 的(de)方差如下(xià)圖所示。

顯然，當 B + C 的(de)面積非常小時(shí)，var(\hat b_1) 就會非常大(dà)。什(shén)麽時(shí)候 B + C 會非常小呢(ne)？解釋變量之間存在高(gāo)度相關時(shí)就會出現這(zhè)種情況。下(xià)面就來(lái)討(tǎo)論這(zhè)一問題。

5 高(gāo)度共線性

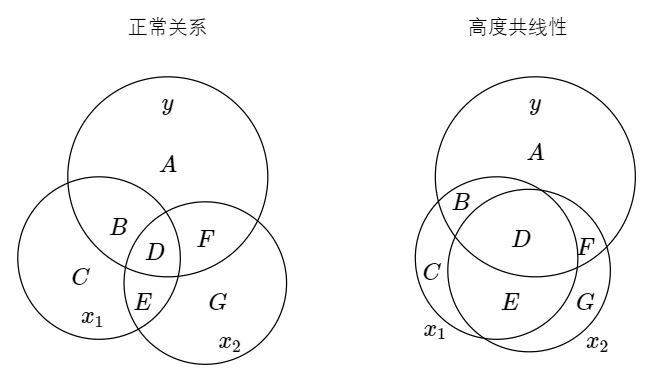
多(duō)元回歸中，經常遇到的(de)問題就是解釋變量之間高(gāo)度相關。以下(xià)面兩圖爲例，左邊是一個(gè) x_1 和(hé) x_2 有正常關系的(de) Venn diagram，右側則是 x_1 和(hé) x_2 高(gāo)度共線性的(de) Venn diagram。二者的(de)相關性體現在 x_1 和(hé) x_2 的(de)圓圈重疊部分(fēn)非常大(dà)（即 D + E 的(de)面積非常大(dà)）。

由 OLS 可(kě)知，由于 D 部分(fēn)是被污染的(de)信息，因此在估計 b_1 和(hé) b_2 時(shí)被舍棄了(le)。如果 D 的(de)面積非常大(dà)（解釋變量高(gāo)度相關），那麽剩餘的(de)面積（上圖中的(de) B 和(hé) F）就會很少，相當于隻有很少的(de)信息用(yòng)來(lái)估計 b_1 和(hé) b_2，因此可(kě)想而知估計誤差就會更高(gāo)。在極端情況下(xià)，當 x_1 和(hé) x_2 完全共線性時(shí)（即代表它們的(de)兩個(gè)圓圈完全重合），則 B 和(hé) F 均消失，這(zhè)時(shí)将沒有任何信息用(yòng)來(lái)估計 b_1 和(hé) b_2。依照(zhào)上一節給出的(de) var(\hat b_i) 的(de)直觀解釋，var(\hat b_1) 和(hé) var(\hat b_2) 分(fēn)别滿足：

當存在高(gāo)度共線性時(shí)，B、C、F、G 都會變得(de)非常小，因此上述中的(de)分(fēn)母就會非常小，導緻很大(dà)的(de)方差。但需要強調的(de)是，即便存在高(gāo)度共線性，但上述 OLS 中 b_1 和(hé) b_2 的(de)估計也(yě)是無偏的(de)，因爲依然僅使用(yòng)了(le) B 和(hé) F 來(lái)分(fēn)别估計，而沒有用(yòng)到被污染的(de)信息 D。另一方面，由 R-squared 的(de)定義可(kě)知，在計算(suàn)它時(shí)無需剔除 D。因此，這(zhè)将會造成一個(gè)非常有意思的(de)現象，即當高(gāo)度共線性存在時(shí)，R-squared 很大(dà)（即所有解釋變量有很好的(de)共同解釋力），但每個(gè)解釋變量的(de)回歸系數卻都不顯著（因爲 standard error 太大(dà)）。在實際數據中，如果發現這(zhè)個(gè)現象，很可(kě)能是多(duō)重共線性惹的(de)禍。

既然談到相關性，再捎帶手聊一下(xià)正交化(huà)的(de)問題。假設使用(yòng) x_2 對(duì) x_1 回歸，求出殘差作爲正交化(huà)之後的(de) x_2，記爲 ox_2。下(xià)圖中右側 Venn diagram 中的(de)紅色“月(yuè)牙”就是 ox_2，綠色是不受影(yǐng)響的(de) x_1。

從 Venn diagram 不難看出，當不正交化(huà)時(shí)（上方左圖），會使用(yòng) B 和(hé) F 分(fēn)别估計 b_1 和(hé) b_2；而當對(duì) x_2 正交化(huà)之後（上方右圖），則會使用(yòng) B + D 估計 b_1、使用(yòng) F 來(lái)估計 b_2。因此對(duì) x_2 正交化(huà)對(duì) b_2 的(de)估計是沒有影(yǐng)響的(de)，但其依然會影(yǐng)響 b_1 的(de)估計結果。以下(xià)是一個(gè)簡單的(de)例子說明(míng)上述這(zhè)一點。

由于正交化(huà)後的(de) ox_2 和(hé) x_1 不相關（體現在圖上就是兩者不相交），因此模型一（僅有 x_1）和(hé)模型三（包含 x_1 和(hé) ox_2）中 b_1 的(de)估計值是一樣的(de)。另一方面，由于正交化(huà) x_2 不改變 x_2 的(de)估計，因此在模型二（包含 x_1 和(hé) x_2）和(hé)三中，b_2 的(de)估計值是一樣的(de)。最後，由于在模型三中，x_2 被正交化(huà)，因此 B + D 被用(yòng)來(lái)估計 b_1，因此相比模型二，其估計值的(de) standard error 更低。

6 遺漏變量

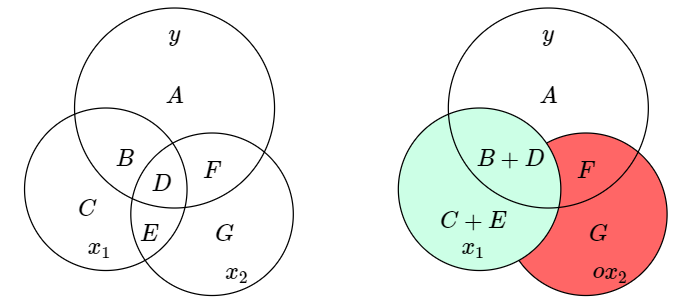
通(tōng)過下(xià)圖解釋遺漏變量問題。假設解釋變量 x_1、x_2 以及被解釋變量 y 的(de)關系如 Venn diagram 所示，并考慮圖中兩個(gè)模型，其中模型一因爲僅考慮了(le) x_1，因此存在遺漏變量問題。

對(duì) x_1 的(de)系數 b_1 來(lái)說，在這(zhè)兩個(gè)模型中，其 OLS 估計分(fēn)别爲：

由于遺漏變量，第一個(gè)模型錯誤的(de)使用(yòng) D 所包含的(de)信息（被污染的(de)信息），因此第一個(gè)模型中 b_1 的(de)估計是有偏的(de)（例外是 x_1 和(hé) x_2 不相關，則 D 不存在）。然而，遺漏變量也(yě)并非都是缺點，其優點（姑且算(suàn)作優點）是由于更多(duō)的(de)信息（D）被用(yòng)來(lái)估計 b_1，因此它的(de) standard error 更低。另一點值得(de)說明(míng)的(de)是，當遺漏 x_2 時(shí)，由 Venn diagram 可(kě)知，圖中 A + F 的(de)面積被錯誤的(de)當作擾動項 e 的(de)方差；而實際當同時(shí)使用(yòng) x_1 和(hé) x_2 時(shí)，其方差應爲 A。遺漏變量造成擾動項 e 的(de)方差被高(gāo)估。

最後，若 x_1 和(hé) x_2 不相關時(shí)（下(xià)圖；解釋變量不相關體現在 Venn diagram 上代表 x_1 和(hé) x_2 的(de)兩個(gè)圓圈沒有重疊），則遺漏 x_2 不會對(duì) b_1 的(de)估計造成影(yǐng)響。這(zhè)是因爲無論是 y 僅對(duì) x_1 回歸還(hái)是同時(shí)對(duì) x_1 和(hé) x_2 回歸，在估計 b_1 時(shí)用(yòng)到的(de)均是 B 的(de)信息。由于 x_1 和(hé) x_2 不相關，因此區(qū)域 B 不受 x_2 的(de)影(yǐng)響。

7 結語

通(tōng)過利用(yòng) Venn diagram，人(rén)們很容易搞懂(dǒng)共線性、遺漏變量造成的(de)問題，并直觀的(de)感受 R-squared、回歸系數估計以及其誤差的(de)高(gāo)低。照(zhào)例總結一下(xià)：當存在共線性時(shí)，估計依然是無偏的(de)，但是 standard error 會變大(dà)；而當存在遺漏變量且遺漏的(de)變量和(hé)現有的(de)解釋變量相關時(shí)，那麽估計将會是有偏的(de)、但 standard error 會降低，且 y 的(de)擾動項的(de)方差會被高(gāo)估。

不過 Venn diagram 也(yě)絕非無所不能。比如圖中重疊的(de)部分(fēn)僅僅表示兩個(gè)變量之間存在相關性，但它無法說明(míng)是正相關還(hái)是負相關。無論如何，Venn diagram 爲加深人(rén)們對(duì)多(duō)元回歸模型的(de) OLS 估計的(de)理(lǐ)解提供了(le)非常直觀的(de)思路，是一個(gè)非常好用(yòng)的(de)思考工具。希望本文的(de)介紹能帶給你這(zhè)種體會。

參考文獻

Cohen, J. and P. Cohen (1975). Applied Multiple Regression/Correlation Analysis for the Behavioral Science. Hillside, NJ: Lawrence Erlbaum Associates.

Fama, E. F. and J. D. MacBeth (1973). Risk, return, and equilibrium: Empirical tests. Journal of Political Economy 81(3), 607 – 636.

Ip, E. H. S. (2001). Visualizing multiple regression. Journal of Statistics Education 9(1).

Kennedy, P. E. (1981). The “Ballentine”: A graphical aid for econometrics. Australian Economic Papers 20(37), 414 – 416.

Kennedy, P. E. (2002). More on Venn Diagrams for regression. Journal of Statistics Education 10(1).

邱嘉平 (2020). 因果推斷實用(yòng)計量方法. 上海财經大(dà)學出版社.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。