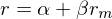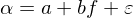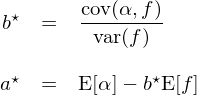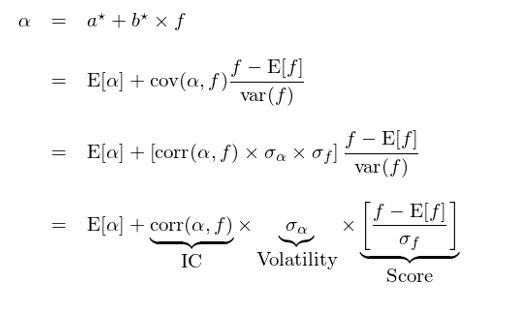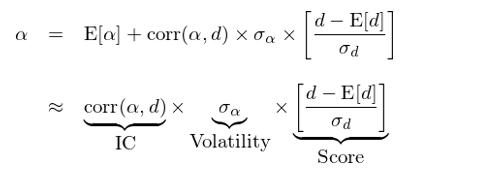作者:石川
1 三要素
主動投資管理(lǐ)的(de)先驅之一 Richard Grinold 寫過一篇著名的(de)文章(zhāng),題爲《α = Volatility × IC × Score》。這(zhè)篇文章(zhāng)标題直白醒目,簡明(míng)扼要的(de)說明(míng)了(le)在主動管理(lǐ)中尋求股票(piào) α 收益率的(de)三要素。
Grinold 對(duì) α 的(de)定義爲個(gè)股收益率中無法被與市場(chǎng)收益率相關的(de) β 部分(fēn)解釋的(de)殘餘部分(fēn)。假設 r 爲個(gè)股相對(duì)無風險收益率的(de)超額收益,r_m 爲市場(chǎng)相對(duì)無風險收益率的(de)超額收益,那麽有
如果個(gè)股的(de) α 都是零(就像 CAPM 假設的(de)那樣),那麽我們買個(gè)指數就萬事大(dà)吉,所有主動型基金經理(lǐ)都會失業。但現實并不是這(zhè)樣,一些股票(piào)的(de)确存在正的(de) α,而另一些存在負的(de) α。主動投資管理(lǐ)就是從所有的(de)股票(piào)中選出擁有超額 α 收益的(de)那些優秀股票(piào)。
讓我們假設爲了(le)挖掘有真正 α 的(de)優秀股票(piào),某主動型基金經理(lǐ)有一個(gè)模型(咱們先甭管這(zhè)個(gè)模型是怎麽得(de)到的(de),也(yě)許是靠著(zhe)手底下(xià)衆多(duō)研究員(yuán)的(de)深度研究,也(yě)許是靠著(zhe)科學的(de)量化(huà)分(fēn)析,也(yě)許是靠打聽(tīng)内部消息,也(yě)許是靠猴子扔飛(fēi)镖,whatever,you name it)。每當這(zhè)個(gè)基金經理(lǐ)要預測個(gè)股下(xià)一期的(de) α 收益時(shí),這(zhè)個(gè)模型便給出一個(gè)預測,記爲 f。
這(zhè)樣 α 的(de)三要素爲 IC、Volatility 以及 Score:
IC:它是對(duì) α 的(de)預測(即 f)和(hé)實際 α 的(de)相關系數,在這(zhè)裏被稱爲信息系數 Information Coefficient。顯然,這(zhè)個(gè)相關度越高(gāo)越好,它最直接的(de)反映基金經理(lǐ)在主動管理(lǐ)中的(de)預測能力。
Volatility:代表的(de)是個(gè)股 α 本身的(de)波動。α 本身的(de)波動越大(dà),說明(míng)越有機會可(kě)圖。舉個(gè)極端的(de)例子,如果 α = 0 或者一個(gè)恒定的(de)常數,那麽這(zhè)支個(gè)股對(duì)所有人(rén)來(lái)說都是一樣的(de),根本沒有 α 可(kě)以挖掘。
Score:這(zhè)是一個(gè)把當期對(duì) α 的(de)預測值 f 按照(zhào)過去的(de)預測進行标準化(huà)後的(de)一個(gè)标準化(huà)分(fēn)數。它代表了(le)在此時(shí)此刻,該基金經理(lǐ)對(duì)這(zhè)支股票(piào)的(de)看好的(de)程度。這(zhè)麽說也(yě)許不夠直白。舉個(gè)例子來(lái)說,假設這(zhè)個(gè)基金經理(lǐ)有一個(gè)非常厲害的(de)模型,每次都能預測個(gè)八九不離十,這(zhè)次的(de)預測值 f 爲 -1%,假設它标準化(huà)後的(de)分(fēn)數爲 -2。因此score就等于 -2,說明(míng)該模型在當期對(duì)這(zhè)支股票(piào)相當不看好。
2 數學含義
在這(zhè)篇文章(zhāng)中,Grinold 雖然使用(yòng)了(le)大(dà)量的(de)例子來(lái)闡述這(zhè)三要素在解釋 α 時(shí)發揮的(de)作用(yòng),但它并沒有具體給出公式 α = Volatility × IC × Score 的(de)推導。下(xià)面我們就來(lái)從數學上說明(míng)這(zhè)個(gè)公式的(de)美(měi)妙之處,它可(kě)以通(tōng)過對(duì) α 收益率以及它的(de)預測值f的(de)曆史時(shí)間序列進行線性回歸來(lái)得(de)到。
用(yòng)時(shí)間序列 f 對(duì)時(shí)間序列 α 做(zuò)線性回歸模型有:
其中,a 和(hé) b 是回歸系數,ε 是回歸誤差,一般假設 ε 的(de)期望爲 0。通(tōng)過曆史數據,利用(yòng)最小二乘法對(duì)上述模型求解可(kě)以得(de)到參數 a 和(hé) b 的(de)最優值:
将得(de)到的(de) a 和(hé) b 的(de)最優參數帶回到上面的(de)回歸模型中,并舍去回歸誤差項,可(kě)得(de):
由于 E[α] 是 α 的(de)曆史均值,對(duì)任何一期的(de) α 都是一樣的(de),因此真正影(yǐng)響 α 的(de)是後面這(zhè)三項的(de)乘積,即 α = IC × Volatility × Score。如果用(yòng)一句話(huà)來(lái)說清楚這(zhè)個(gè) α 公式的(de)含義就是:如果股票(piào)本身有 α 可(kě)以挖掘(α 的(de) Volatility 波動率大(dà))、我有一個(gè)準确的(de)預測方法(在曆史上預測值 f 和(hé) α 之間的(de) IC 高(gāo)),并且當期我的(de)預測值 f 非常好(我對(duì)這(zhè)個(gè)股票(piào)非常有信心),那麽我就可(kě)以預期這(zhè)支股票(piào)在未來(lái)有不錯的(de)超額收益 α。
在這(zhè)三要素中,α 自身的(de)波動由股票(piào)所處的(de)行業和(hé)公司的(de)性質所決定。更能反映基金經理(lǐ)本事的(de)是長(cháng)期的(de)預測能力(IC)以及在當前的(de)判斷(Score)。在我看來(lái),高(gāo)IC是最重要的(de)條件,否則不管 Score 多(duō)高(gāo),如果模型壓根就不能有效的(de)預測 α(低 IC),那麽一切都是枉然。當然,如果有了(le)高(gāo)的(de) IC,那麽我們隻需要找到在當前時(shí)刻的(de)預測中 Score 高(gāo)的(de)那些股票(piào)買入即可(kě)。所以,所有靠選股爲生的(de)主動型基金經理(lǐ)大(dà)概都在較勁腦(nǎo)汁的(de)想找到一個(gè)可(kě)以提高(gāo) IC 的(de) α 預測模型或者方法。
3 另一種形式
Grinold 最初提出的(de) α 三因素公式就如同前面小節所說明(míng)的(de)那樣,我們預測的(de)是 α 本身,回歸時(shí)是在時(shí)間維度對(duì)預測值f的(de)時(shí)間序列和(hé)實際 α 的(de)時(shí)間序列進行回歸。然而預測 α 本身終究是困難的(de),更常見的(de)做(zuò)法是尋找能夠挖掘 α 收益率的(de)因子,使用(yòng)因子本身的(de)值對(duì) α 建模,并通(tōng)過截面回歸來(lái)分(fēn)析這(zhè)類模型是否具有挖掘 α 的(de)能力,這(zhè)就是 α 三因素公式的(de)變種。
截面回歸是在給定的(de)時(shí)間節點,使用(yòng)所有股票(piào)在該時(shí)點在某一因子上的(de)取值對(duì)下(xià)一時(shí)刻股票(piào)的(de) α 收益進行回歸分(fēn)析。令向量 d 爲所有股票(piào)在時(shí)刻 t 的(de)因子暴露,α 爲所有股票(piào)在 t+1 時(shí)刻的(de) α 收益率向量,利用(yòng)線性回歸便可(kě)以得(de)到與本文第二節中相似的(de)結果:
雖然公式看起來(lái)很相似,但這(zhè)裏的(de)解釋略有不同:E[α] 是所有股票(piào)在 t+1 時(shí)刻的(de)期望 α 收益,它應該近似的(de)等于 0。IC 是該因子和(hé) α 的(de)截面相關系數,它衡量在 t 時(shí)刻,該因子是否具備優秀的(de)選股能力。Volatility 是所有股票(piào) α 收益的(de)截面波動率,它描述的(de)是個(gè)股 α 收益率的(de)差異性。Score 衡量個(gè)股在因子上取值的(de)強弱。
總結來(lái)說,因子和(hé) α 收益率的(de)相關性越高(gāo),個(gè)股 α 的(de)差異性越大(dà),我們的(de)選股基礎就越好。在這(zhè)個(gè)基礎上,隻需要按照(zhào)該因子選出分(fēn)數高(gāo)的(de)股票(piào)就可(kě)以預期得(de)到超額的(de) α 收益。如果所有股票(piào)的(de) α 都一樣(Volatility = 0)或者所有股票(piào)的(de)因子取值都一樣(Score = 0),那麽上式就相當于 α = 0,也(yě)就是說根本無法通(tōng)過該因子選出含有超額 α 收益的(de)股票(piào);隻有因子和(hé) α 收益率的(de)相關性越高(gāo),股票(piào)的(de)差異性越大(dà)(α 和(hé)因子的(de)差異性都是越大(dà)越好),才越有可(kě)能找出 α。
截面回歸方法往往是一種事後驗證。即我們在已知 t+1 時(shí)刻所有股票(piào)的(de) α 的(de)前提下(xià),用(yòng) t 時(shí)刻的(de)因子取值對(duì) α 進行回歸,以此來(lái)衡量該因子在t時(shí)刻的(de)選股能力。然而,由于不同因子之間有相關性,這(zhè)種衡量方法其實也(yě)是有一定缺陷的(de)。此外,t 時(shí)刻的(de)選股能力更不能保證在 t+1 時(shí)刻該因子仍然有同樣的(de)選股能力。要正确判斷一個(gè)因子的(de)選股能力仍然需要從時(shí)間維度上的(de)考察通(tōng)過該因子構造的(de)純因子投資組合(即排除其他(tā)因子對(duì)目标因子的(de)幹擾)是否可(kě)以持續的(de)獲得(de)超額收益。
免責聲明(míng):入市有風險,投資需謹慎。在任何情況下(xià),本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià),本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外,文中圖表均直接或間接來(lái)自于相應論文,僅爲介紹之用(yòng),版權歸原作者和(hé)期刊所有。