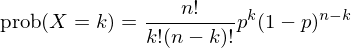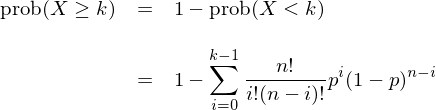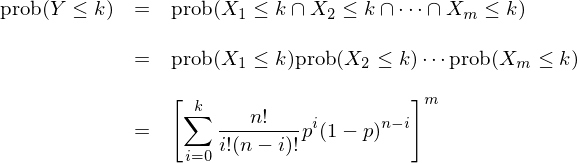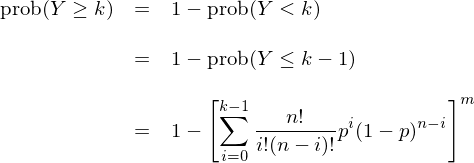出色不如走運？

作者：石川

1 巴菲特的(de)類比

1984 年，沃倫•巴菲特在介紹格倫厄姆和(hé)多(duō)德的(de)價值投資流派時(shí)，舉了(le)下(xià)面這(zhè)個(gè)例子：

它的(de)意思是說：假設全美(měi)國 2.7 億人(rén)都下(xià)注 1 美(měi)元來(lái)猜扔硬币的(de)結果（猜對(duì)的(de)概率是50%），猜對(duì)的(de)人(rén)得(de)到 2 塊錢，猜錯的(de)人(rén)出局。在此後的(de)每一輪中，仍未被淘汰的(de)人(rén)繼續押注它們的(de)所有賭資，猜對(duì)後賭資翻倍，猜錯出局，以此類推。這(zhè)樣，10 輪過後，大(dà)概還(hái)會剩下(xià) 26 萬人(rén)（即 10 輪全部猜對(duì)）；20 輪後，2.7 億人(rén)中還(hái)會剩下(xià) 250 人(rén)左右（即 20 輪全部猜對(duì)）。有 250 人(rén)連續猜對(duì) 20 輪扔硬币的(de)結果，多(duō)麽不可(kě)思議(yì)！

連續猜對(duì) 20 輪後，剩餘的(de)這(zhè)些人(rén)将會有超過 1 百萬美(měi)元！連續猜對(duì) 20 次，打敗了(le)剩下(xià)的(de)近 2.7 億人(rén)，從 1 元輕松賺到 100萬，這(zhè)些人(rén)聽(tīng)起來(lái)簡直就像是天選之人(rén)！但他(tā)們的(de)成就真的(de)是出于他(tā)們自身的(de)某種特質，還(hái)僅僅是依靠運氣呢(ne)？

巴菲特想通(tōng)過這(zhè)個(gè)故事表達的(de)道理(lǐ)還(hái)沒有講完，但讓我們先把它放下(xià)，先來(lái)看看下(xià)面這(zhè)個(gè)簡單的(de)計算(suàn)。

2 僅靠運氣勝出的(de)“牛人(rén)”

如果你從大(dà)街(jiē)上随便抓一個(gè)人(rén)，然後讓他(tā)連續猜 20 次硬币的(de)正反，那麽他(tā)全部猜對(duì)的(de)概率微乎其微（順便說一句，如果你真的(de)碰上這(zhè)麽一個(gè)全猜對(duì)的(de)牛人(rén)，那麽他(tā)很可(kě)能是真牛逼！）。但是，如果許多(duō)許多(duō)人(rén)一起猜硬币，那麽是否一定會從中脫穎出來(lái)一個(gè)“牛人(rén)”呢(ne)？這(zhè)樣找出來(lái)的(de)“牛人(rén)”是否可(kě)信呢(ne)（即他(tā)是真牛還(hái)是僅僅是運氣呢(ne)）？這(zhè)些問題可(kě)以通(tōng)過下(xià)面的(de)概率模型來(lái)回答(dá)。

對(duì)于一個(gè)人(rén)來(lái)說，假設他(tā)猜扔硬币的(de)結果 n 次，每次猜對(duì)的(de)概率爲 p（p = 0.5），不同次猜的(de)結果相互獨立。那麽，這(zhè)個(gè)人(rén)在 n 次中猜對(duì) k 次的(de)概率符合二項分(fēn)布。令 X 表示這(zhè)個(gè)人(rén)猜對(duì)的(de)次數。顯然，它是一個(gè)随機變量，滿足以下(xià)概率質量函數（probability mass function）：

如果以這(zhè)個(gè)人(rén)猜對(duì)個(gè)數的(de)多(duō)少來(lái)衡量他(tā)是否厲害，那麽我們關心的(de)則是他(tā)在 n 次中至少猜對(duì) k 次的(de)概率，即：

接下(xià)來(lái)，我們找來(lái)了(le)好多(duō)好多(duō)人(rén)，一共有 m 位。我們想看看這(zhè) m 個(gè)人(rén)裏面最厲害的(de)人(rén)猜對(duì)次數的(de)概率分(fēn)布。根據我們對(duì)厲害的(de)定義，這(zhè) m 個(gè)人(rén)裏面最厲害的(de)一定是在這(zhè)些人(rén)中猜對(duì)次數最多(duō)的(de)那一個(gè)。因此，如果用(yòng) Y 代表這(zhè)個(gè)最厲害的(de)人(rén)在 n 次中猜對(duì)的(de)個(gè)數，那麽不難發現，Y 和(hé)每個(gè)人(rén)猜對(duì)次數 X 的(de)關系爲 Y = max(X_1, X_2, …, X_m)。這(zhè)其中 Xi 是第 i 個(gè)人(rén)猜對(duì)的(de)次數。在這(zhè)種關系下(xià)，不難推導出 Y 的(de)累積分(fēn)布函數（cumulative distribution function）：

由此不難計算(suàn)出最厲害的(de)人(rén)至少猜對(duì) k 次的(de)概率，即 Y ≥ k 的(de)概率：

同樣，我們也(yě)可(kě)以從 CDF 反推出 Y 的(de)PMF：

得(de)到 PMF 後，我們可(kě)以求出 Y 的(de)期望和(hé)方差：

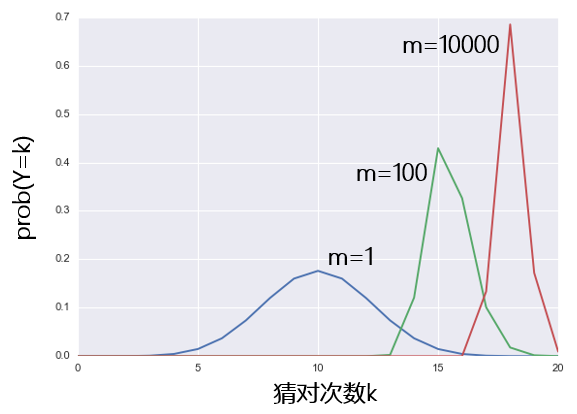
下(xià)面我們就來(lái)看看，随著(zhe)人(rén)數的(de)增多(duō)，最厲害的(de)人(rén)猜對(duì) k 次的(de)概率，即 prob(Y = k)，是如何随人(rén)數 m 變化(huà)的(de)。令輪次 n = 20，猜對(duì)概率 p = 0.5，下(xià)圖分(fēn)别表示了(le)當我們有 1 個(gè)人(rén)，100 個(gè)人(rén)，以及 10000 個(gè)人(rén)猜硬币時(shí)，Y 的(de)概率分(fēn)布。

可(kě)以明(míng)顯的(de)看出，随著(zhe)參與人(rén)數的(de)增多(duō)，Y 的(de)概率質量函數（pmf）在橫坐(zuò)标軸上向右移動，且變的(de)越來(lái)越窄。Y 的(de) pmf 向右平移說明(míng)随著(zhe)人(rén)數的(de)增多(duō)，最厲害之人(rén)的(de)水(shuǐ)平越來(lái)越高(gāo)：當隻有 1 個(gè)人(rén)猜時(shí)，他(tā)猜對(duì) 10 次的(de)概率最高(gāo)（因爲每次有二分(fēn)之一的(de)概率猜對(duì)，一共猜 20 次）；當人(rén)數上升到 100 人(rén)時(shí)，他(tā)們之中猜的(de)最好的(de)那個(gè)人(rén)最有可(kě)能猜對(duì) 15 次；當有 10000 人(rén)同時(shí)猜時(shí)，最好的(de)那個(gè)最有可(kě)能猜對(duì) 18 次。這(zhè)正所謂“水(shuǐ)漲船高(gāo)”。Y 的(de) pmf 變窄說明(míng)它的(de)标準差越來(lái)越小；換句話(huà)說，随著(zhe)人(rén)數的(de)增多(duō)，我們對(duì)于這(zhè)其中最厲害人(rén)猜對(duì)的(de)個(gè)數的(de)判斷将越來(lái)越有信心。

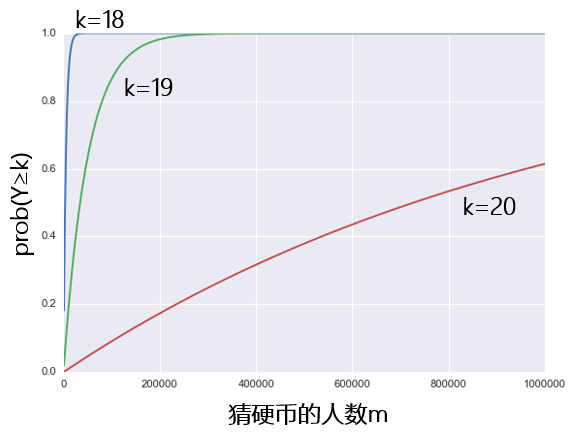
下(xià)面再讓我們來(lái)看看最厲害的(de)人(rén)至少猜對(duì) k 次的(de)概率，即 prob(Y ≥ k)，是如何随人(rén)數 m 變化(huà)的(de)。下(xià)圖分(fēn)别爲 k 取 18，19 以及 20 的(de)情況（輪次仍然是一共 20 輪）。比如，綠色曲線表示的(de)是 prob(Y ≥ 19) 是如何随 m 變化(huà)的(de)。可(kě)以看到，在參與的(de)人(rén)數大(dà)約爲 30 萬人(rén)時(shí)，最厲害之人(rén)至少猜對(duì) 19 輪的(de)概率就已經非常接近 1。換句話(huà)說，我們可(kě)以斷言，如果有 30 萬人(rén)同時(shí)參與猜硬币的(de)遊戲，那麽一定會至少有一個(gè)人(rén)從中脫穎而出，猜對(duì)至少 19 輪。當 k = 20（即 20 輪全部猜對(duì)）時(shí)，prob(Y ≥ 20) 的(de)概率也(yě)是随 m 單調遞增的(de)，雖然速度比起 k = 19 時(shí)要慢(màn)得(de)多(duō)。當 1 百萬人(rén)同時(shí)猜硬币的(de)時(shí)候，最厲害的(de)那個(gè)人(rén)有超過 60% 的(de)概率猜對(duì)全部的(de) 20 輪。

從上面的(de)結果不難發現，當越來(lái)越多(duō)的(de)人(rén)參與猜硬币的(de)遊戲後，總會出現一個(gè)或者多(duō)個(gè)最厲害的(de)“天選之人(rén)”，會全部猜對(duì)，令衆粉絲驚呼。這(zhè)些人(rén)也(yě)許會将這(zhè)種幸運誤以爲是自己的(de)天生神力；也(yě)許還(hái)會開始在自媒體上大(dà)肆曝光(guāng)、出書(shū)、給迷信的(de)人(rén)講座、開啓網紅之路、站上人(rén)生巅峰。殊不知這(zhè)這(zhè)種結果的(de)出現僅僅是靠運氣（pure luck），一切皆枉然。

3 投資界

上面這(zhè)個(gè)例子在證券投資界也(yě)有著(zhe)完美(měi)的(de)體現。下(xià)面這(zhè)類場(chǎng)景你一定不陌生：每年末在各大(dà)基金或者陽光(guāng)私募排行的(de)榜單上，都有收益率嗷嗷牛叉的(de) top 10。又或者在民間量化(huà)平台（諸如果仁網）首頁上的(de)推薦策略中，各種上榜的(de)策略那無論從回測還(hái)是到實盤，其業績讓人(rén)看來(lái)都啧啧稱奇，感歎這(zhè)些人(rén)賺錢簡直如探囊取物(wù)一般簡單。

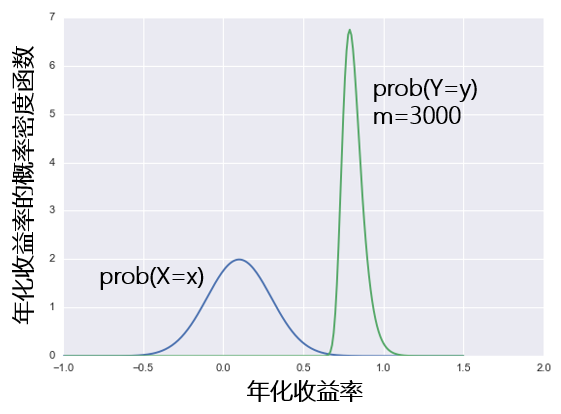
相信看過猜硬币的(de)例子後你能夠明(míng)白，這(zhè)些上榜的(de)例子和(hé)猜硬币中的(de)那些最厲害的(de)人(rén)并沒有太大(dà)的(de)差異。爲了(le)進一步說服你，讓我們假設一個(gè)股票(piào)型投資策略的(de)年化(huà)收益率 X 符合均值爲 10%，标準差爲 20% 的(de)正态分(fēn)布。假設市場(chǎng)中有 m 支股票(piào)型基金，則它們中最好的(de)那個(gè)的(de)收益率 Y 是 X 的(de)函數，Y = max(X_1, X_2, …, X_m)。類似上節中的(de)計算(suàn)不難得(de)到關于 Y 的(de)概率分(fēn)布和(hé)各種統計值。比如，下(xià)圖是當有 3000 支基金時(shí)，其中最好的(de)那個(gè)的(de)收益率分(fēn)布和(hé)單獨一支基金收益率分(fēn)布的(de)比較：和(hé)猜硬币的(de)例子一樣，最好的(de)那支的(de)收益率分(fēn)布在橫坐(zuò)标上向右移動且變的(de)更窄。

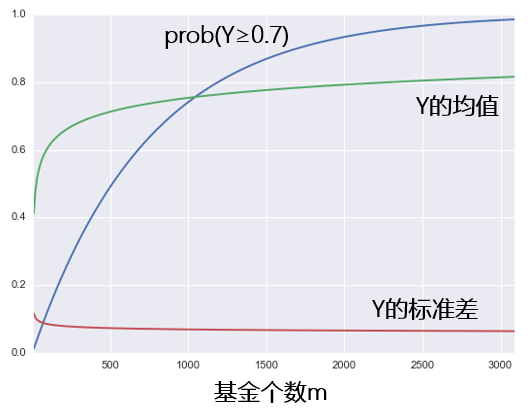
下(xià)圖爲 prob(Y ≥ 0.7) ——最好的(de)那個(gè)基金的(de)年化(huà)收益率超過 70% 的(de)概率——随基金個(gè)數 m 變化(huà)的(de)結果。同時(shí)，我們也(yě)給出了(le) Y 的(de)均值和(hé)标準差随 m 的(de)變化(huà)。随著(zhe) m 的(de)增大(dà)，prob(Y ≥ 0.7) 向 1 逼近（即我們越來(lái)越确定總會有一些基金脫穎而出，年化(huà)收益率超過 70%）。這(zhè)種判斷也(yě)同樣可(kě)以被 Y 的(de)均值和(hé)方差來(lái)證明(míng)：随著(zhe)基金個(gè)數的(de)增大(dà)，最好的(de)基金的(de)年化(huà)收益率的(de)均值也(yě)在增加，且标準差在減小。

這(zhè)個(gè)結果告訴我們，看到各種榜單上無敵的(de)産品根本不足爲奇。但我們内心真正關心的(de)問題是：這(zhè)些上榜的(de)基金取得(de)的(de)優異業績靠的(de)到底是運氣（比如評比的(de)當年的(de)市場(chǎng)恰好适合它們的(de)策略），還(hái)是一套真正的(de)科學投資體系？看看基金的(de)排名，不禁讓人(rén)心灰意冷(lěng)。

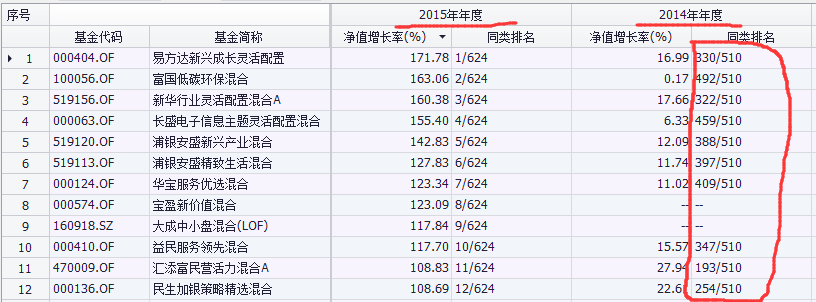
下(xià)圖爲 2015 年淨值增長(cháng)最高(gāo)的(de)前 12 支偏股混合型基金。這(zhè)些在 2015 年風光(guāng)無限的(de)基金在 2014 年如何呢(ne)？可(kě)謂慘不忍睹。我不想不負責任的(de)基于此就認爲這(zhè)些基金 2015 年的(de)表現純粹是來(lái)自運氣。但同樣的(de)，如果讓我來(lái)選基金，我也(yě)不會把投資人(rén)的(de)錢輕易的(de)就交給它們管理(lǐ)。畢竟，短期的(de)“運氣”無法說明(míng)任何“能力”。這(zhè)不是“實力強”，而是“人(rén)生狀态比較好”。

4 巴菲特的(de)深意

下(xià)面我們回頭來(lái)看巴菲特的(de)例子。他(tā)通(tōng)過猜硬币的(de)例子真正想說明(míng)的(de)是，如果猜對(duì)的(de) 250 個(gè)人(rén)僅僅憑借的(de)是運氣，那麽按照(zhào)随機性，這(zhè)些人(rén)應該來(lái)自美(měi)國的(de)各個(gè)不同的(de)地方。但是，如果這(zhè)些人(rén)裏面有大(dà)一部分(fēn)（遠(yuǎn)超過随機性所對(duì)應的(de)數字）來(lái)自一個(gè)名爲“格倫厄姆和(hé)多(duō)德的(de)小鎮”呢(ne)？那就要好好看看這(zhè)些出自該小鎮的(de)人(rén)擁有哪些共同的(de)特質。

衆所周知，格倫厄姆和(hé)多(duō)德是價值投資的(de)開山鼻祖，而巴菲特無異于最好的(de)繼承者。他(tā)通(tōng)過這(zhè)個(gè)例子想要說明(míng)的(de)是，價值投資是一個(gè)經過風雨(yǔ)考驗的(de)科學投資系統，這(zhè)些真正掌握該系統的(de)人(rén)會長(cháng)屹立于證券投資之林(lín)，這(zhè)些人(rén)在投資界可(kě)以做(zuò)到靠真正的(de)能力來(lái)持續的(de)“猜對(duì)硬币”（賺到錢）。

時(shí)間才是檢驗一個(gè)基金或者一個(gè)基金經理(lǐ)是否優異的(de)唯一标準。

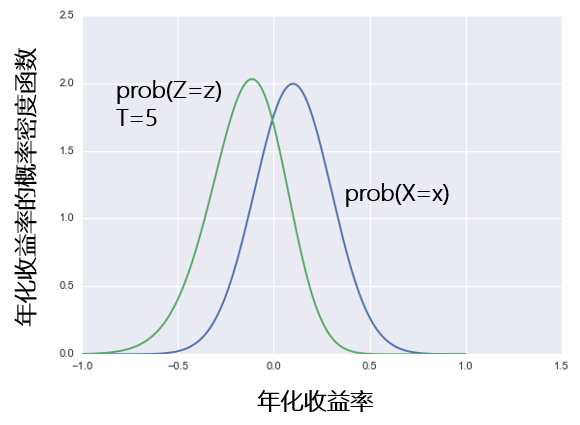
爲此，我們從時(shí)間維度再做(zuò)最後一個(gè)實驗。我們仍然假設一個(gè)基金年化(huà)收益率 X 的(de)分(fēn)布符合正态分(fēn)布。此外，我們考慮該基金在連續 T 年内中最差的(de)那一年的(de)收益率作爲評價該基金水(shuǐ)平的(de)一個(gè)标準，令 Z 代表這(zhè)個(gè)收益率，因此我們有 Z = min(X_1, X_2, …, X_T)。

假設該基金的(de)年化(huà)收益率爲 N(0.2, 0.3)，并令 T = 5 年。Z 的(de)分(fēn)布如下(xià)圖所示。Z 的(de)均值爲 -14.4%，标準差爲 20.0%。最差年份中，期望收益爲虧損 14% 以上。面對(duì) 20% 的(de)期望收益，恐怕沒有人(rén)想遇到這(zhè)樣的(de)年景。

這(zhè)支基金年化(huà)收益率的(de)期望有 20%，似乎足夠吸引人(rén)。但是，之所以産生這(zhè)麽差的(de)結果是因爲該基金年化(huà)收益率分(fēn)布的(de)标準差太大(dà)（我們假設 0.3）。标準差是用(yòng)來(lái)衡量一支基金的(de)穩定程度，那自然越小越好；越小說明(míng)年與年之間，它的(de)表現越穩定。

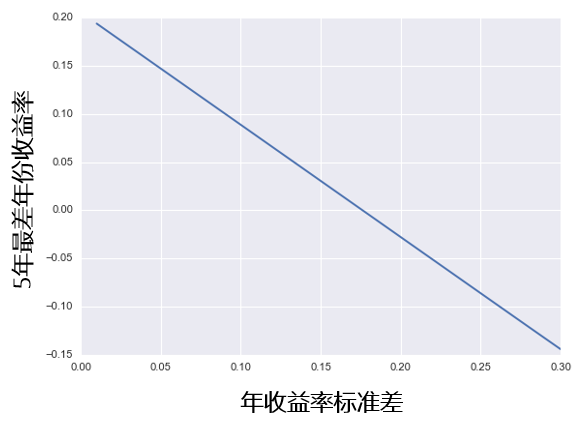
這(zhè)個(gè)結論不難證明(míng)。假設其他(tā)條件不變而僅改變收益率标準差後，得(de)到的(de) Z 的(de)均值如下(xià)圖所示，可(kě)見标準差越小（即基金的(de)水(shuǐ)平越穩定），最差年份的(de)收益率才會越高(gāo)。

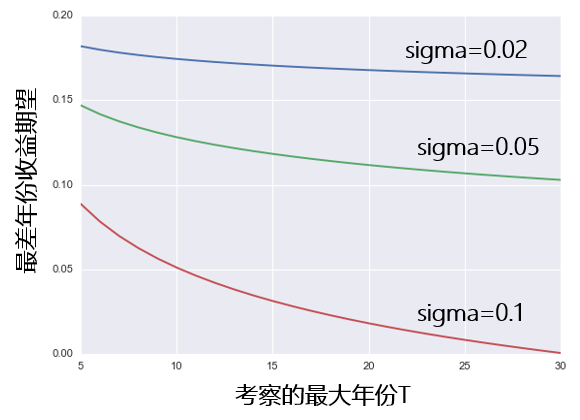
時(shí)間永遠(yuǎn)是穩定性最大(dà)的(de)敵人(rén)。上面的(de)實驗僅僅考慮了(le) 5 年的(de)情況。如果我們把時(shí)間拉長(cháng)又會怎樣呢(ne)？不同的(de)收益率标準差能否禁得(de)起時(shí)間的(de)考驗呢(ne)？下(xià)圖顯示了(le)标準差分(fēn)别爲 2%，5%，以及 10% 的(de)情況（收益率期望仍然爲 20%），時(shí)間跨度從5年到30年。當一個(gè)基金足夠穩健（标準差爲 2%），它在 30 年内的(de)最差收益的(de)期望也(yě)不會差到哪裏。但如果它不夠穩健（标準差爲 10%），它的(de)表現一定是會在時(shí)間面前褪色的(de)。

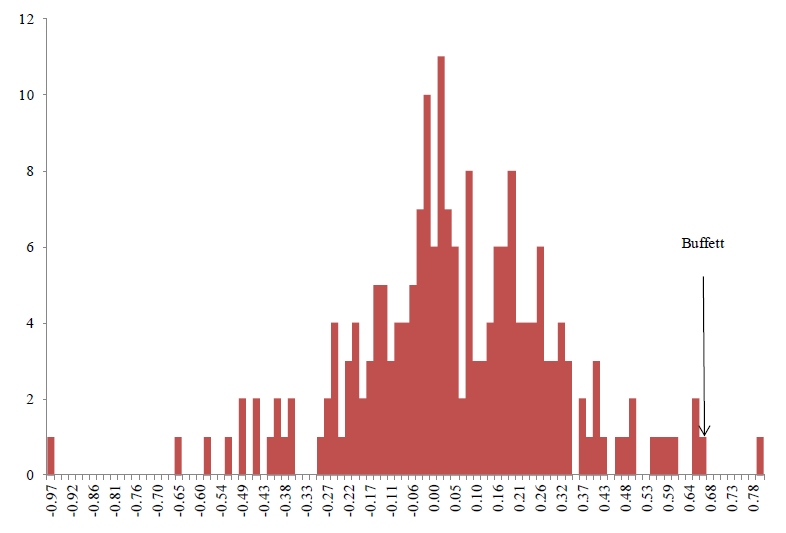
時(shí)間又從來(lái)都是一個(gè)科學投資體系的(de)朋友。上圖同時(shí)說明(míng)，随著(zhe)時(shí)間的(de)正常，這(zhè)三個(gè)不同 sigma 的(de)曲線之間的(de)差距逐漸增大(dà)。這(zhè)說明(míng)，如果僅僅看短期（3 到 5 年），我們還(hái)無法準确的(de)判斷濫竽充數者，但它們一定會在時(shí)間的(de)沖刷下(xià)原形畢露的(de)。但是，我們國内的(de)基金又有多(duō)少有 10 年甚至更長(cháng)的(de)曆史呢(ne)？那些“著名”的(de)基金經理(lǐ)又有多(duō)少有記載可(kě)回溯的(de) track record 呢(ne)？在這(zhè)種背景下(xià)就來(lái)大(dà)搞 MOM 和(hé) FOF，在我看來(lái)是國内投資界所面對(duì)的(de)困擾。再來(lái)看看巴菲特的(de)表現。下(xià)圖是美(měi)國擁有 30 年以上曆史的(de)基金的(de)信息率（類似夏普率）分(fēn)布圖。在 30 年尺度的(de)丈量下(xià)，巴菲特的(de)表現有目共睹（排名第二）。這(zhè)也(yě)許是對(duì)來(lái)自“格倫厄姆和(hé)多(duō)德小鎮”的(de)投資者最好的(de)褒獎。

5 結語

優秀的(de)業績是靠運氣還(hái)是來(lái)自實力？時(shí)間是評判這(zhè)一切的(de)唯一标準。面對(duì)一個(gè)潛在的(de)好的(de)策略或者基金産品，我們切記不要被它完美(měi)的(de)業績所迷惑雙眼，必須時(shí)刻保持理(lǐ)智，冷(lěng)靜的(de)對(duì)其曆史業績進行業績歸因，客觀的(de)考量投資團隊以及風控體系。這(zhè)一切有不得(de)半點馬虎，來(lái)不得(de)半點急躁。

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。