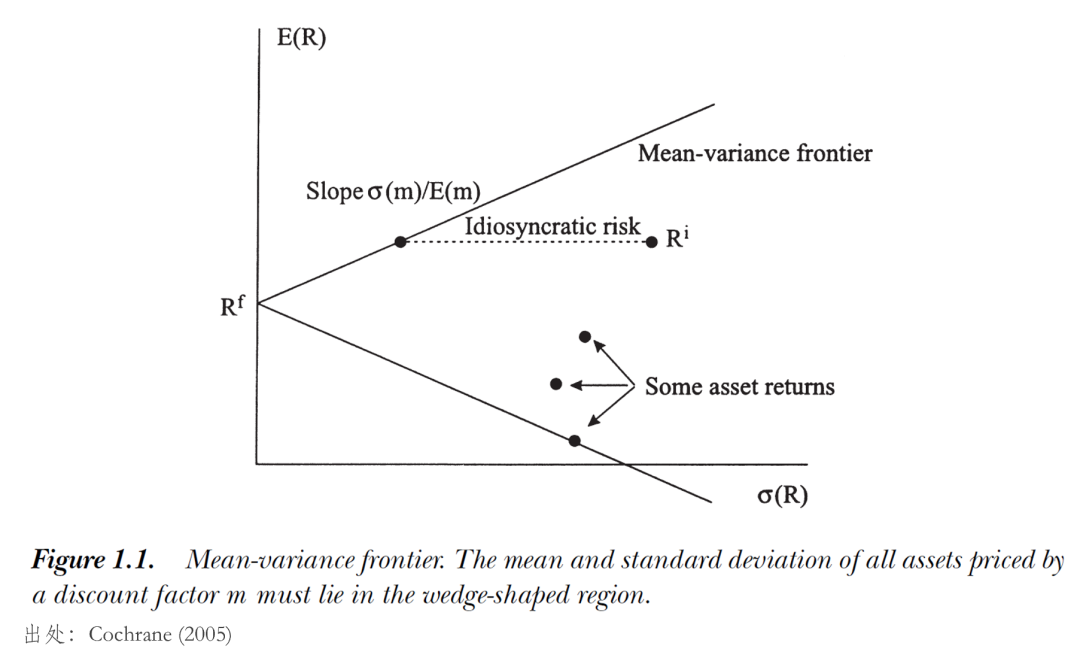
尋找 Mean-Variance Frontier

發布時(shí)間：2021-04-27 | 來(lái)源: 川總寫量化(huà)

作者：石川

摘要：資産定價理(lǐ)論保證了(le) SDF 和(hé) mean-variance frontier 的(de)等價性。機器學習(xí)在估計 SDF 方面或大(dà)有可(kě)爲。

前文《FF3們背後的(de)資産定價理(lǐ)論》介紹了(le) Stochastic Discount Factor（SDF）和(hé)多(duō)因子模型之間的(de)等價關系。今天我們再來(lái)說說 SDF 和(hé) mean-variance (efficient) frontier 的(de)等價性。

依然考慮超額收益，由資産定價理(lǐ)論有 $0 = \mbox{E}[mR^e]$ ，其中 $m$ 爲 SDF， $R^e$ 爲某資産的(de)超額收益。将該式進行如下(xià)代數運算(suàn)：

$\begin{array}{rll} 0&=&\displaystyle \mbox{E}[mR^e]\\ &=&\displaystyle \mbox{E}[m]\mbox{E}[R^e]+\mbox{cov}(m, R^e)\\ &=&\displaystyle \mbox{E}[m]\mbox{E}[R^e]+\rho(m,R^e)\sigma(m)\sigma(R^e)\\ \end{array}$

因而有：

$\displaystyle\frac{\mbox{E}[R^e]}{\sigma(R^e)}=-\frac{\rho(m, R^e)\sigma(m)}{\mbox{E}[m]}$

由于相關系數的(de)取值範圍是 -1 到 +1，因此任意資産的(de)超額收益和(hé) SDF 之間滿足以下(xià)關系，它被稱爲 Hansen-Jagannathan bound（Hansen and Jagannathan 1991）：

$\displaystyle\frac{|\mbox{E}[R^e]|}{\sigma(R^e)}\le\frac{\sigma(m)}{\mbox{E}[m]}$

若我們隻關心 $\mbox{E}[R^e]>0$ 的(de)資産，則可(kě)以把絕對(duì)值符号去掉：

$\displaystyle\frac{\mbox{E}[R^e]}{\sigma(R^e)}\le\frac{\sigma(m)}{\mbox{E}[m]}$

上式左側正是夏普率（Sharpe Ratio）的(de)定義，因此該不等式意味著(zhe)資産的(de)夏普率是有上限的(de)。觀察該不等式，我們關心兩個(gè)問題：（1）什(shén)麽時(shí)候等号成立？（2）等号成立意味著(zhe)什(shén)麽？問題（1）的(de)答(dá)案很簡單，當 $\rho(m,R^e)=- 1$ 時(shí)等式成立。對(duì)于問題（2），等号成立意味著(zhe)該資産位于 mean-variance frontier 之上（因爲這(zhè)些資産的(de)夏普率最大(dà)），且這(zhè)些資産和(hé) SDF 的(de)相關系數都爲 -1。這(zhè)意味著(zhe)所有 mean-variance frontier 上的(de)資産都和(hé) SDF 完全負相關，因而它們都是完全正相關。

這(zhè)種相關性意味著(zhe) SDF 和(hé)位于 mean-variance frontier 之上任意資産收益率（記爲 $R^{mv}$ ）的(de)等價關系： $m=a+bR^{mv}$ 。

假設無風險資産（ $R_f$ ）存在，則 mean-variance frontier 是通(tōng)過 $R_f$ 和(hé) tangency portfolio 的(de)直線，其上任何一個(gè)非 $R_f$ 資産都可(kě)以用(yòng)來(lái)構造 SDF。此外，利用(yòng) SDF 和(hé) mean-variance frontier 的(de)等價關系，可(kě)以得(de)到如下(xià)這(zhè)個(gè)特殊的(de)單因子模型：

$\displaystyle\mbox{E}[R^e]=\beta\lambda_{R^{mv}}$

其中 $\lambda_{R^{mv}}$ 是 $R^{mv}$ 的(de) risk premium， $\beta$ 爲資産超額收益對(duì) mean-variance frontier 上資産超額收益的(de)回歸系數。這(zhè)就是資産定價中的(de) Roll (1977) Theorem。通(tōng)過 SDF 和(hé)多(duō)因子模型的(de)等價性，以及 SDF 和(hé) mean-variance frontier 的(de)等價性，也(yě)就得(de)到多(duō)因子模型和(hé) mean-variance frontier 的(de)等價性 —— mean-variance frontier 上資産的(de)收益率能夠表達爲多(duō)因子模型中因子收益率的(de)線性組合。

Any asset pricing model is the same as the statement that there is some return on the mean-variance frontier. If Fama and French (1993)’s asset pricing model is correct, it means that there is a combination of their MKT, SMB and HML portfolios that is on the mean-variance frontier. The CAPM is simply the statement that the market return is on the mean-variance frontier. —— John Cochrane

再看一眼 $\mbox{E}[R^e]=\beta\lambda_{R^{mv}}$ ，它長(cháng)得(de)非常像 CAPM，CAPM 隻不過是假設市場(chǎng)組合在 mean-variance frontier 上。這(zhè)種等價性也(yě)可(kě)以用(yòng)于比較不同的(de)多(duō)因子模型。如果模型 A 的(de)因子構造的(de)最大(dà)夏普率高(gāo)于模型 B 的(de)因子構造的(de)夏普率，那麽前者就優于後者，這(zhè)和(hé) Barillas and Shanken (2017) 提出的(de)方法也(yě)很好的(de)契合（見《Toward a better factor model》）。

寫到這(zhè)裏，先總結一下(xià)上述内容（因爲接下(xià)來(lái)就要上“正餐”了(le)）。資産定價理(lǐ)論告訴我們 SDF 和(hé) mean-variance frontier 是等價的(de)，因此隻要找到 mean-variance frontier 上的(de)任意（非 $R_f$ ）資産，就找到了(le) SDF 并給所有資産定價。當然，這(zhè)僅僅是把尋找 SDF 的(de)問題轉化(huà)爲尋找位于 mean-variance efficient (MVE) portfolio 的(de)問題，但人(rén)們并不知道 MVE portfolio 中不同股票(piào)的(de)權重是怎樣的(de)。

從實證研究的(de)角度，利用(yòng) SDF，mean-variance frontier 以及多(duō)因子模型三者的(de)等價關系可(kě)以将上述問題大(dà)大(dà)簡化(huà)，即通(tōng)過多(duō)因子模型來(lái)研究 SDF 和(hé)資産定價。雖然不同的(de)多(duō)因子模型都是根據不同的(de)理(lǐ)論（比如 discount dividend model 或者行爲金融學理(lǐ)論）提出的(de)，但最終比較不同的(de)模型時(shí)，看的(de)還(hái)是哪個(gè)模型的(de)因子算(suàn)出的(de)夏普率更高(gāo)。

然而，由于研究傳統傳承，因子通(tōng)常都是通(tōng)過 double-sort 構造的(de)，導緻通(tōng)過因子算(suàn)出的(de)最大(dà)夏普率（在樣本外）并不高(gāo)，所以沒少被人(rén)诟病。鑒于這(zhè)個(gè)現象，一個(gè)自然的(de)問題就是能否繞過多(duō)因子模型，直接使用(yòng)資産（i.e., 股票(piào)）來(lái)研究 SDF。答(dá)案是肯定的(de)。由于因子收益率是一攬子資産收益率的(de)加權平均，而 SDF 可(kě)以表達爲因子收益率的(de)線性函數，因此 SDF 自然也(yě)可(kě)以寫成資産收益率的(de)線性組合。

正如《實證資産定價理(lǐ)論新進展》的(de)第五節介紹的(de)那樣，直接使用(yòng)資産研究 SDF 正是近年來(lái)的(de)研究重點之一，例如 Kozak, Nagel and Santosh (2020) 和(hé) Bryzgalova, Pelger and Zhu (2020) 都是這(zhè)方面的(de)力作。而我今天想要談的(de)是 Chen, Pelger and Zhu (2020)。這(zhè)篇文章(zhāng)有很多(duō)令人(rén)驚喜的(de)地方，但最大(dà)的(de)創新無疑是把機器學習(xí)中的(de) Generative Adversarial Network（GAN）巧妙地用(yòng)在了(le)資産定價場(chǎng)景中。

爲了(le)讓各位小夥伴充分(fēn)感受這(zhè)篇論文的(de)魅力，下(xià)面話(huà)不多(duō)說，先上 5 張 slides，它們高(gāo)度概括了(le)該文的(de)核心（來(lái)自 Markus Pelger 在 2020 Utah Winter Finance Conference 上做(zuò)的(de)報告；參考文獻最後有視頻(pín)連接），我看後的(de)感受就是一個(gè)字 —— 旺德福！

OK！接下(xià)來(lái)爲了(le)便于理(lǐ)解，對(duì)每頁 slide 作簡要介紹（但是非常建議(yì)去看報告視頻(pín) + 閱讀論文原文）。

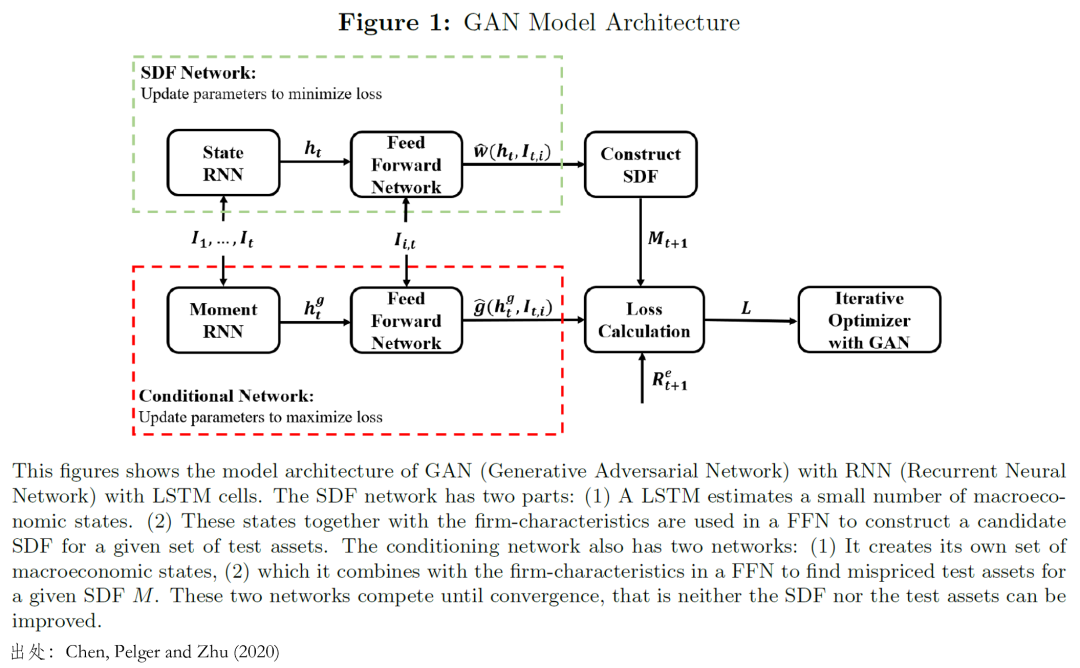
首先前兩頁介紹了(le)該文的(de)模型。在第一頁中，該文明(míng)确指出其研究的(de)是 conditional model（注意期望符号 $\mbox{E}_t$ 的(de)下(xià)标 $t$ ）。對(duì)于 conditional model，可(kě)以通(tōng)過加入工具變量把 conditional moment conditions 轉化(huà)成 unconditional moment conditions（具體數學背景見 Cochrane 2005 的(de)第 8 章(zhāng)）。接下(xià)來(lái)第二頁， $t+1$ 期的(de) SDF（記爲 $M_{t+1}$ ）被表達爲股票(piào)超額收益的(de)線性函數：

$M_{t+1}=1-\sum_{i=1}^N w_{i,t}R^e_{i,t+1}$

其中 $w_{i,t}$ 是根據 $t$ 時(shí)刻所有信息來(lái)确定的(de)股票(piào)的(de)權重。在 Chen, Pelger and Zhu (2020) 的(de)模型中， $w_{i,t}$ 被視爲宏觀經濟變量 $I_t$ 和(hé)公司特征（firm characteristics） $I_{i,t}$ 的(de)非線性函數，是通(tōng)過機器學習(xí)模型求解的(de)對(duì)象。

第三頁将 SDF 和(hé) mean-variance frontier 聯系了(le)起來(lái)；一旦得(de)到 SDF 的(de)參數 $w$ ，就同時(shí)得(de)到了(le) MVE portfolio，即文中的(de) SDF portfolio。利用(yòng) SDF portfolio 的(de) risk premium，并計算(suàn)個(gè)股和(hé)它的(de) $\beta$ 就可(kě)以得(de)到單因子模型，檢驗其定價能力或選股。

第四、五兩頁是模型的(de)估計。第四頁首先在給定的(de)工具變量下(xià)，把 moment conditions 轉化(huà)爲 no-arbitrage loss function，然後通(tōng)過 feed forward network 算(suàn)法估計模型的(de)參數，最小化(huà) moment conditions（moment conditions 代表了(le) pricing errors）。如何選擇工具變量呢(ne)？

在該文的(de)模型中，工具變量 $\hat I_{t}$ 可(kě)以理(lǐ)解成由宏觀經濟變量和(hé) firm characteristics 決定的(de) conditioning variables，因而 $R^e_{t+1}\hat I_{t}$ 則代表了(le) managed portfolios。舉個(gè)例子，比如某個(gè)工具變量是判别股票(piào)是否是小市值的(de) indicator variable（小市值爲 1，大(dà)市值爲 0），那麽它就意味著(zhe)我們希望 SDF 的(de)最優參數能夠更好的(de)給小市值股票(piào)定價（即通(tōng)過小市值股票(piào)構造的(de) managed portfolios 的(de) pricing error 最小）。所以，挑選工具變量構造 managed portfolios 就相當于挑選 test assets。這(zhè)裏，工具變量的(de)應用(yòng)和(hé) Kelly, Pruitt and Su (2019) 提出的(de) IPCA 方法也(yě)有異曲同工之妙。

對(duì)資産定價來(lái)說，并非所有 test assets 在估計 SDF 時(shí)都能發揮同樣的(de)作用(yòng)，我們關心的(de)是那些包含最多(duō)定價信息的(de) test assets。最關鍵的(de)來(lái)了(le)：爲了(le)實現這(zhè)個(gè)目标，Chen, Pelger and Zhu (2020) 使用(yòng)了(le) GAN（生成對(duì)抗網絡，一種非監督式學習(xí)算(suàn)法，通(tōng)過讓兩個(gè)神經網絡相互博弈的(de)方式進行學習(xí)），通(tōng)過兩個(gè)模型交替叠代來(lái)同時(shí)估計 SDF 和(hé)選擇工具變量：

1. SDF 模型在給定的(de)工具變量下(xià)，以最小化(huà) test assets 的(de) pricing errors 爲目标确定 SDF 的(de)參數 $w$ ；

2. 工具變量模型在給定的(de) SDF 下(xià)，以最大(dà)化(huà) pricing errors 爲目标選擇新的(de)工具變量 $\hat I$ 。

和(hé)傳統 GMM 主要從 efficiency 出發挑選工具變量相比，該文的(de)方法強調挑選工具變量時(shí)的(de)經濟學意義和(hé)穩健性，此外深度學習(xí)算(suàn)法能夠同時(shí)處理(lǐ)更多(duō)的(de)參數。以上就是對(duì)這(zhè) 5 頁 slides 的(de)簡要說明(míng)。但是，本文的(de)解讀無論如何也(yě)取代不了(le)閱讀原文。如果你覺著(zhe)原文太長(cháng)，那麽至少聽(tīng)一聽(tīng) Markus Pelger 的(de)報告。

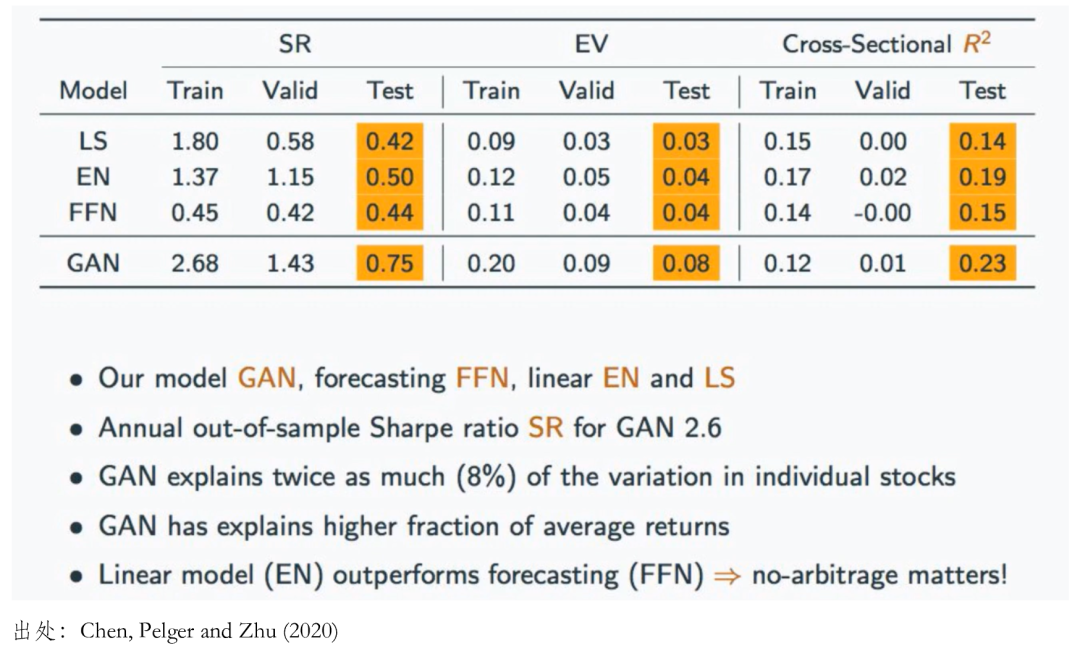
最後給出部分(fēn)實證結果。相比于其他(tā)方法，該文構造的(de) SDF 在樣本外的(de)夏普率最高(gāo)，且無論是時(shí)序上解釋資産收益率波動（EV）還(hái)是截面上解釋資産預期收益率差異（cross-sectional $R^2$ ）都更加優秀。

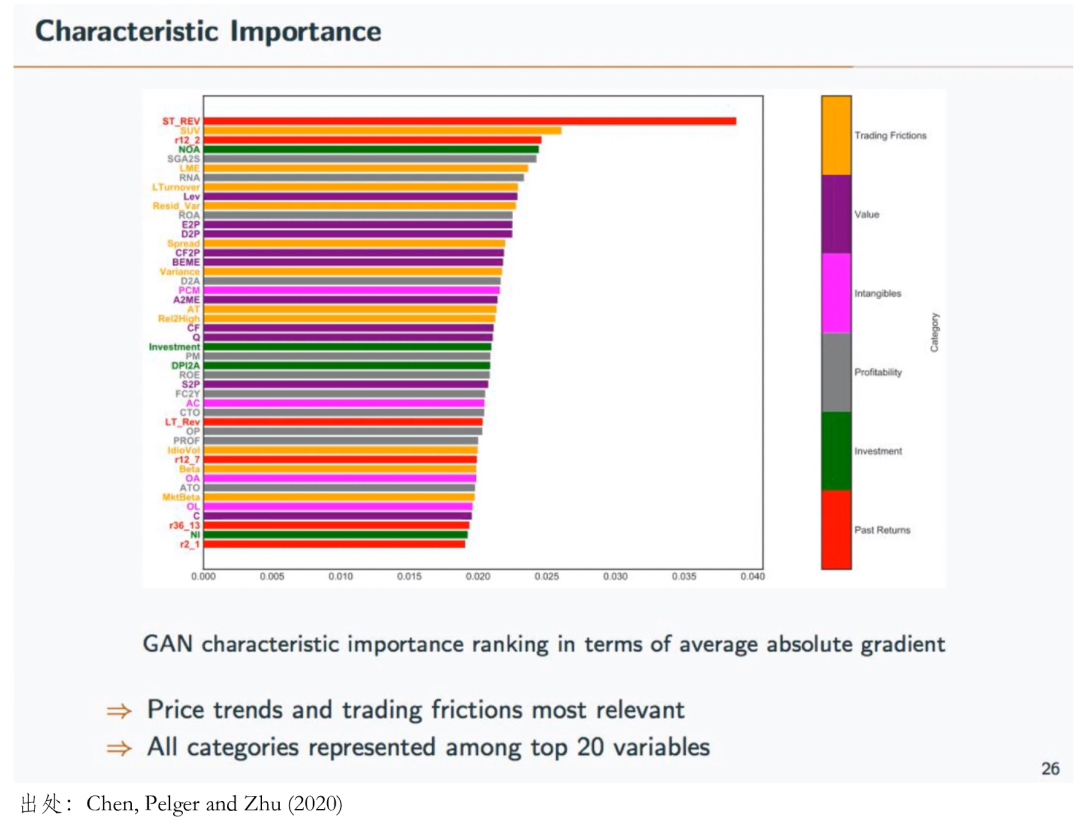
在所有考察的(de) firm characteristics 中，下(xià)面這(zhè)些是最重要的(de)，且它們代表了(le)包括交易摩擦，價值，無形資産，盈利，投資以及動量（反轉）這(zhè)些常見的(de)大(dà)類因子，說明(míng)包含這(zhè)些因子的(de)主流多(duō)因子模型也(yě)都是靠譜的(de)。

毋庸置疑，Chen, Pelger and Zhu (2020) 是一篇值得(de)研讀和(hé)學習(xí)的(de)文章(zhāng)（它獲得(de)了(le) UWFC 2020 Best Paper Award，出現在頂刊隻是時(shí)間問題）。近年來(lái)，越來(lái)越多(duō)學者把機器學習(xí)算(suàn)法成功應用(yòng)到資産定價研究中，而 Chen, Pelger and Zhu (2020) 是其中的(de)重要代表之一（更多(duō)相關研究見《實證資産定價理(lǐ)論新進展》和(hé)《因子投資：方法與實踐》的(de) 6.8 節）。

從業界實務的(de)角度來(lái)說，使用(yòng)曆史數據求解 mean-variance optimization 就可(kě)以得(de)到夏普率最大(dà)的(de)組合，但由于各種 estimation errors 以及使用(yòng)的(de)是曆史數據，這(zhè)個(gè)最優解（基本上）沒有意義；而構造樣本外 MVE portfolio 才是人(rén)們所追求的(de)。在這(zhè)方面，學術界的(de)諸多(duō)将機器學習(xí)算(suàn)法用(yòng)于估計 SDF 的(de)研究成果将給人(rén)們全新的(de)啓發。

參考文獻

Barillas, F. and J. Shanken (2017). Which alpha? Review of Financial Studies 30(4), 1316 – 1338.

Bryzgalova, S., M. Pelger, and J. Zhu (2020). Forest through the trees: Building cross-sections of stock returns. Working paper.

Chen, L., M. Pelger, and J. Zhu (2020). Deep learning in asset pricing. Working paper.

Cochrane, J. H. (2005). Asset Pricing (Revised Edition). Princeton, NJ: Princeton University Press.

Fama, E. F. and K. R. French (1993). Common risk factors in the returns on stocks and bonds. Journal of Financial Economics 33(1), 3 – 56.

Hansen, L. P. and R. Jagannathan (1991). Implications of security market data for models of dynamic economics. Journal of Political Economy 99(2), 225 – 262.

Kelly, B. T., S. Pruitt, and Y. Su (2019). Characteristics are covariances: A unified model of risk and return. Journal of Financial Economics 134(3), 501 – 524.

Kozak, S., S. Nagel, and S. Santosh (2020). Shrinking the cross-section. Journal of Financial Economics 135(2), 271 – 292.

Roll, R. (1977). A critique of the asset pricing theory's tests Part I: On past and potential testability of the theory. Journal of Financial Economics 4(2), 129 – 176.

https://www.youtube.com/watch?v=ioKYA3UZ70E

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。

合格投資者聲明(míng)

尋找 Mean-Variance Frontier