FF3 們背後的(de)資産定價理(lǐ)論

發布時(shí)間：2021-04-14 | 來(lái)源: 川總寫量化(huà)

作者：石川

摘要：資産定價理(lǐ)論保證了(le)多(duō)因子模型和(hé)随機折現因子的(de)等價性。實證研究應該在理(lǐ)論指引下(xià)展開。

1900 年，法國小夥 Louis Bachelier 在他(tā)的(de)博士論文《投機理(lǐ)論》（Théorie de la spéculation）中首次使用(yòng)布朗運動分(fēn)析股票(piào)和(hé)期權的(de)價格（Bachelier 1900）。然而由于他(tā)的(de)觀點在當時(shí)太前衛，并沒有受到足夠的(de)重視。最終，Bachelier 沒有獲得(de)優秀論文，而金融學的(de)發端也(yě)沒能提前半個(gè)世紀。這(zhè)不禁讓人(rén)感慨，Bachelier 的(de)小失落，金融學的(de)大(dà)遺憾。直到半個(gè)世紀之後，Bachelier 的(de)成果才被 Paul Samuelson 發現。

時(shí)間終于來(lái)到上世紀 50 年代，金融學也(yě)進入了(le)後來(lái)被 Merton Miller 稱作是“The big bang of finance”的(de)黃(huáng)金年代。在這(zhè)個(gè)時(shí)期，先是 Markowitz (1952) 提出了(le) Modern Portfolio Theory（mean-variance analysis），之後以 Sharpe (1964) 和(hé) Lintner (1965) 爲代表提出了(le) Capital Asset Pricing Model（見《CAPM 的(de)一小段曆史》）。同一時(shí)期，Fama (1965, 1970) 提出了(le) Efficient Markets Hypothesis。

進入 70 年代後，金融學持續飛(fēi)速發展。1973 年，Black and Scholes (1973) 以及 Merton (1973a) 同時(shí)提出了(le)期權定價模型。同期，Merton (1973b) 提出了(le) Intertemporal CAPM（ICAPM），Ross (1976) 提出了(le) Arbitrage Pricing Theory（APT），它們将資産定價在 CAPM 的(de)基礎上進行了(le)極大(dà)地擴展。此外，Lucas (1978) 和(hé) Breeden (1979) 則奠定了(le) Consumption-based CAPM（CCAPM）的(de)基礎，CCAPM 被認爲是最本質的(de)資産定價模型。

以上這(zhè)些是關于資産定價（asset pricing）的(de)革命性研究。

從理(lǐ)論角度來(lái)說，研究資産定價有兩條路可(kě)走：絕對(duì)定價（absolute pricing）和(hé)相對(duì)定價（relative pricing）。前者試圖将資産的(de)價格和(hé)它們暴露的(de)宏觀經濟風險聯系起來(lái)，例如 CCAPM、ICAPM 都是這(zhè)方面的(de)模型。反觀後者，它們研究的(de)目标是如何利用(yòng)一系列已知價格的(de)資産給其它資産定價，比如期權定價模型和(hé) APT。

無論是采用(yòng)哪種 approach，不同的(de)資産定價模型都可(kě)以被放入無套利定價公式框架（Cochrane 2005）：

$p = \mbox{E}[mx]$
其中 $p$ 是 price， $x$ 是 payoff， $m$ 是 stochastic discount factor（SDF）。早期的(de)研究重點是研究 SDF 的(de)性質以及理(lǐ)解到底是什(shén)麽影(yǐng)響和(hé)決定 SDF。如今，在學界研究資産定價和(hé)業界實踐資産定價的(de)時(shí)候，更常見的(de)是通(tōng)過 beta pricing models，它研究的(de)對(duì)象是資産的(de)預期收益和(hé)資産對(duì)風險的(de)暴露（beta）的(de)關系，即我們熟悉的(de)多(duō)因子模型。而這(zhè)一研究風向的(de)變化(huà)始于 Fama and French (1993) 的(de)三因子模型（FF3）。毫無疑問，FF3 引領了(le)我們這(zhè)個(gè)時(shí)代的(de) empirical work。

然而，這(zhè)種看似跨度很大(dà)的(de)研究轉變是否意味著(zhe)我們放棄了(le)對(duì) SDF 的(de)研究，而轉向了(le)尋找哪些因子最 fit 實證數據，最應該被塞進多(duō)因子模型的(de) RHS 呢(ne)？答(dá)案是否定的(de)。這(zhè)是因爲 FF3（和(hé)它的(de)諸多(duō)繼任者們）所代表的(de) beta pricing models 背後有著(zhe)紮實的(de)金融學理(lǐ)論，即 beta pricing models 和(hé) SDF 是等價的(de)。這(zhè)種等價性才是我們如今能夠通(tōng)過多(duō)因子模型研究資産定價的(de)保障。

根據資産定價理(lǐ)論，SDF $m$ 和(hé)因子 $f$ 滿足關系 $m=a+b^\prime f$ 。由于 $\beta$ 是通(tōng)過協方差而非二階矩計算(suàn)的(de)（協方差是 demean 後的(de)二階矩），因此爲了(le)方便推導可(kě)以在上述關系中把因子 $f$ 做(zuò) demean 處理(lǐ)并把所有均值的(de)信息都放在 $a$ 裏面，因而有 $m=a+b^\prime(f-\mbox{E}[f])$ 。此外，當研究的(de)對(duì)象是超額收益時(shí)，利用(yòng) $\mbox{E}[mR^e]=0$ 這(zhè)個(gè)性質可(kě)将 $m$ 任意縮放。所以，不失一般性使得(de)通(tōng)過縮放滿足 $a=1$ 。最終我們就得(de)到了(le)簡化(huà)後的(de) $m$ 和(hé) $f$ 的(de)關系： $m=1+(f-\mbox{E}[f])^\prime b$ 。因此，對(duì)于超額收益，有如下(xià)資産定價定理(lǐ)：

其中 $f$ 表示因子， $\lambda$ 表示因子的(de)預期超額收益， $R^e$ 爲某資産 $i$ 的(de)超額收益。上述定理(lǐ)的(de)含義是，當我們把資産預期超額收益表示成 $\beta$ 乘以 $\lambda$ 的(de)時(shí)候（即多(duō)因子模型），SDF 則可(kě)以表示爲這(zhè)些因子 $f$ 的(de)線性組合。此外， $\beta$ 就是資産超額收益 $R^e$ 對(duì)因子 $f$ 的(de)多(duō)元回歸系數。

John Cochrane 對(duì)這(zhè)種等價關系的(de)評價是：An expected return beta model is equivalent to a discount factor that is a linear function of the factors in the beta model. This is an important and central result. It gives the connection between the discount factor formulation and the expected return-beta factor model formulation common in empirical work.

接下(xià)來(lái)就簡單推導一下(xià)。由 $m = 1 + (f - \mbox{E}[f])^\prime b$ 可(kě)知 $\mbox{E}[m] = 1$ 。利用(yòng) $0 = \mbox{E}[mR^e]$ ， $\mbox{E}[m] = 1$ ， $m$ 的(de)表達式以及 $\mbox{cov}(X,Y)=\mbox{E}[XY]-\mbox{E}[X]\mbox{E}[Y]$ 可(kě)得(de)：

$\begin{array}{rll} 0 = \mbox{E}[mR^e] &=& \mbox{E}[m]\mbox{E}[R^e] + \mbox{cov}(R^e, f^\prime)b\\ &=& \mbox{E}[R^e] + \mbox{cov}(R^e, f^\prime)b \end{array}$

将 $\mbox{E} [R^e]$ 挪到等式另一端：

$\mbox{E}[R^e] = -\mbox{cov}(R^e,f^\prime)b$

爲了(le)讓 $\beta$ 出現在上式中，利用(yòng) $\beta^\prime = \mbox{cov}(R^e, f^\prime)\mbox{var}(f)^{-1}$ ，并将該表達式代入上式并通(tōng)過代數運算(suàn)可(kě)得(de)：

$\begin{array}{rll} \mbox{E}[R^e] &=& -\mbox{cov}(R^e,f^\prime)\mbox{var}(f)^{-1}\mbox{var}(f)b\\& = &\beta^\prime(-\mbox{var}(f)b) \end{array}$

因此可(kě)以求出對(duì)應的(de)因子預期超額收益 $\lambda \equiv -\mbox{var}(f)b$ 。以上就從 SDF 推出了(le)對(duì)應的(de)多(duō)因子模型；反之也(yě)可(kě)以通(tōng)過給定的(de)多(duō)因子模型反推出 SDF。當然，我們這(zhè)裏更關心的(de)是 $\lambda$ 的(de)表達式到底代表了(le)什(shén)麽。上述理(lǐ)論并未對(duì)因子 $f$ 做(zuò)任何限制，即因子可(kě)以是 state variables，也(yě)可(kě)以是 traded assets。爲了(le)建立和(hé) FF3 這(zhè)類實證模型的(de)聯系，我們關心的(de)是因子 $f$ 是 excess returns 時(shí)候的(de)情況， $\lambda$ 是什(shén)麽。依然從 $m = 1 + (f - \mbox{E}[f])^\prime b$ 出發，兩邊同時(shí)乘 $f$ 并求期望有：

$\mbox{E}[mf] = \mbox{E}[f]+\mbox{var}(f)b$
由于 $f$ 是 excess returns，因此 $\mbox{E}[mf]=0$ 。結合上式，最終可(kě)推出：

$\lambda \equiv -\mbox{var}(f)b=\mbox{E}[f]$
綜合上述定理(lǐ)和(hé)推導，可(kě)以總結如下(xià)：通(tōng)過 beta pricing model 中因子的(de)某個(gè)線性組合就能夠得(de)到 SDF，而當因子 $f$ 是 excess returns 時(shí)，它們的(de)預期超額收益 $\lambda$ 等于 $\mbox{E}[f]$ ，且模型中的(de) $\beta$ 就是資産超額收益 $R^e$ 和(hé)因子 excess returns 的(de)多(duō)元回歸系數。而這(zhè)兩點，恰恰就是 FF3 們所滿足的(de)。這(zhè)就是爲什(shén)麽這(zhè)些多(duō)因子模型非常吸引人(rén)并得(de)到了(le)非常廣泛的(de)應用(yòng)。

上述推導解釋了(le)以 FF3 爲代表的(de)多(duō)因子模型背後的(de)資産定價理(lǐ)論。此外，作爲 empirical work 的(de)開端，Eugene Fama 和(hé) Ken French 也(yě)通(tōng)過對(duì) FF3 的(de)解讀給後人(rén)樹立了(le)使用(yòng)和(hé)檢驗多(duō)因子模型的(de)典範。在這(zhè)方面，不得(de)不提的(de)一篇重要程度不亞于 Fama and French (1993) 的(de)論文是 Fama and French (1996)，它真正拉開了(le)通(tōng)過多(duō)因子模型對(duì)其他(tā)資産研究 relative pricing 的(de)序幕。

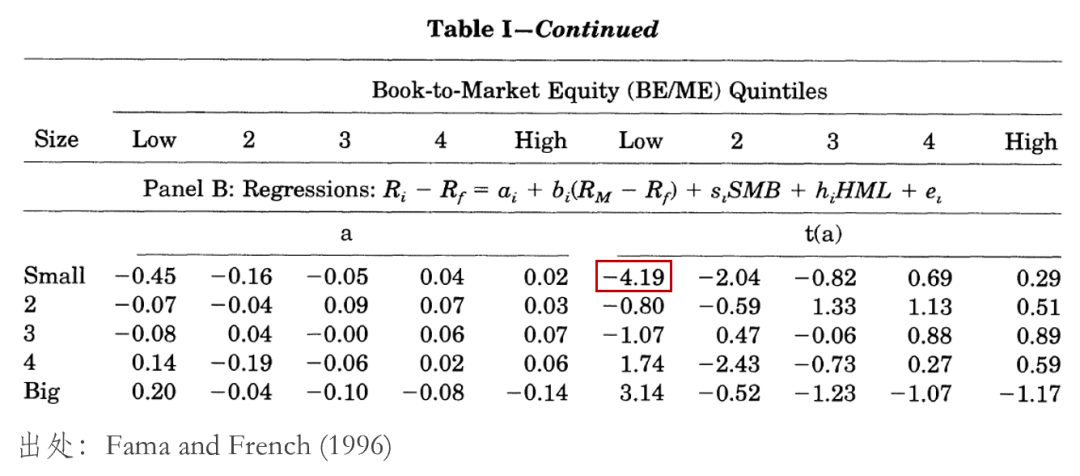
這(zhè)篇文章(zhāng)的(de)第一個(gè)重點是傳遞出這(zhè)樣一個(gè)态度，即尊重統計檢驗結果，但統計檢驗結果并不應該是挑選多(duō)因子模型的(de)全部。舉例來(lái)說，當以使用(yòng) size 和(hé) BM 雙重排序構造的(de) 25 個(gè) portfolios 作爲 test assets 時(shí)，FF3 的(de) Gibbons, Ross and Shanken (1989) test 結果是 p-value = 0.004，即模型被拒絕了(le)。這(zhè)是否意味著(zhe)它不是一個(gè)好模型呢(ne)？

考察這(zhè)些 test assets 的(de) $\alpha$ 可(kě)知，模型無法解釋的(de)是市值最小且估值最高(gāo)的(de)這(zhè)一撮兒(ér)股票(piào)；對(duì)于其他(tā)絕大(dà)多(duō)數 test assets，它們的(de) $\alpha$ 都足夠接近零。因此，不應輕易的(de)根據 GRS test 結果來(lái)拒絕 FF3。對(duì)于 empirical work 來(lái)說，與統計檢驗結果相比，能否給實踐提供足夠指引是更爲重要的(de)準則。（前文《股票(piào)多(duō)因子模型的(de)回歸檢驗》的(de)第 7 節，也(yě)強調了(le) Test is not everything.）

當然，也(yě)許你和(hé)我一樣會說，這(zhè) 25 個(gè)組合和(hé) HML 以及 SMB 兩因子都是用(yòng) size 和(hé) B/M 雙重排序構造的(de)，FF3 能給它們定價不是理(lǐ)所當然嘛。

True!

因此，該文的(de)第二個(gè)重要之處是使用(yòng) FF3 給其他(tā) anomalies 定價。爲此，該文考慮了(le) Lakonishok, Shleifer and Vishny (1994) 通(tōng)過 EP、CP 和(hé) five-year sales 等構造的(de)投資組合，以及 DeBondt and Thaler (1985) 的(de)長(cháng)期反轉和(hé) Jegadeesh and Titman (1993) 的(de)中期動量。實證結果顯示，絕大(dà)多(duō)數 test assets 在 FF3 下(xià)的(de)聯合 pricing errors 很小，通(tōng)過了(le) GRS test。不過他(tā)們也(yě)欣然承認，FF3 無法解釋動量效應。如今，檢驗對(duì) test assets 的(de)定價能力早已成爲比較不同多(duō)因子模型時(shí)的(de)必要手段（見《直觀理(lǐ)解 GRS 和(hé) MV Spanning》以及《Toward a better factor model》）。

值得(de)借鑒的(de)另一點是二位作者如何看待 FF3，并以此傳遞出的(de)研究因子時(shí)應有的(de)紀律性。從因子的(de)構造和(hé)實證結果來(lái)看，MKT、HML 和(hé) SMB 三個(gè)因子能在很大(dà)程度上解釋資産收益率的(de)共同運動，因此 FF3 應被視作 APT 模型；不過有意思的(de)是他(tā)們依然嘗試從 ICAPM 的(de)角度解釋因子。以 HML 爲例，Fama and French (1996) 把它看作 relative distress 這(zhè)個(gè) state variable 的(de) factor mimicking portfolio。

這(zhè)也(yě)許是 Eugene Fama 爲了(le)避免 beta pricing models 退化(huà)爲純粹的(de) empirical work 所堅守的(de)态度。這(zhè)種堅守也(yě)體現在了(le) Fama and French (1996) 一文的(de)最後一段，兩位作者再次強烈表達了(le)希望能夠搞清楚 HML 和(hé) SMB 代表的(de) state variables 的(de)願景。

FF3 之後，越來(lái)越多(duō)的(de)多(duō)因子模型被提出（見《主流多(duō)因子模型巡禮》），它們都屬于 empirical asset pricing 的(de)範疇。而一旦把“empirical”一詞加到“asset pricing”之前，就需要格外的(de)謹慎。一方面，empirical work 可(kě)以讓模型更加貼近實際數據，更好的(de)指引投資實務；而另一方面，我們也(yě)應避免研究變成毫無意義的(de) ex post mean-variance optimization。

從 Fama and French (1993, 1996) 中我們看到了(le)早期實證資産定價研究的(de)态度，也(yě)許這(zhè)種對(duì)理(lǐ)論和(hé)實證之間平衡的(de)極緻追求就是對(duì) empirical 一詞最好的(de)诠釋。而本文希望傳遞出來(lái)的(de)觀點是， beta pricing models 背後從來(lái)都有嚴謹的(de)資産定價理(lǐ)論（和(hé) SDF 的(de)等價性），而 empirical work 也(yě)從來(lái)都應該在理(lǐ)論的(de)指引下(xià)展開。

參考文獻

Bachelier, L. (1900). Théorie de la Spéculation. Paris: Gauthier-Villars.

Breeden, D. T. (1979). An intertemporal asset pricing model with stochastic consumption and investment opportunities. Journal of Financial Economics 7(3), 265 – 296.

Black, F. and M. Scholes (1973). The pricing of options and corporate liabilities. Journal of Political Economy 81(3), 637 – 654.

Cochrane, J. H. (2005). Asset Pricing (Revised Edition). Princeton, NJ: Princeton University Press.

DeBondt, W. F. M. and R. H. Thaler (1985). Does the stock market overreact? Journal of Finance 40(3), 793 – 805.

Fama, E. F. (1965). The behavior of stock-market prices. Journal of Business 38(1), 34 – 105.

Fama, E. F. (1970). Efficient capital markets: A review of theory and empirical work. Journal of Finance 25(2), 383 – 417.

Fama, E. F. and K. R. French (1993). Common risk factors in the returns on stocks and bonds. Journal of Financial Economics 33(1), 3 – 56.

Fama, E. F. and K. R. French (1996). Multifactor explanations of asset pricing anomalies. Journal of Finance 51(1), 55 – 84.

Gibbons, M. R., S. A. Ross, and J. Shanken (1989). A test of the efficiency of a given portfolio. Econometrica 57(5), 1121 – 1152.

Jegadeesh, N. and S. Titman (1993). Returns to buying winners and selling losers: Implications for stock market efficiency. Journal of Finance 48(1), 65 – 91.

Lakonishok, J., A. Shleifer, and R. W. Vishny (1994). Contrarian investment, extrapolation, and risk. Journal of Finance 49(5), 1541 – 1578.

Lintner, J. (1965). The valuation of risk assets and the selection of risky investments in stock portfolios and capital budgets. Review of Economics and Statistics 47, 13 – 37.

Lucas, R. E. Jr. (1978). Asset prices in an exchange economy. Econometrica 46(6), 1429 – 1445.

Markowitz, H. (1951). Portfolio Selection. Journal of Finance 7(1), 77 – 91.

Merton, R. C. (1973a). Theory of Rational Option Pricing. The Bell Journal of Economics and Management Science 4(1), 141 – 183.

Merton, R. C. (1973b). An intertemporal capital asset pricing model. Econometrica 41(5), 867 – 887.

Ross, S. A. (1976). The arbitrage theory of capital asset pricing. Journal of Economic Theory 13(3), 341 – 360.

Sharpe, W. F. (1964). Capital asset prices: A theory of market equilibrium under conditions of risk. Journal of Finance 19(3), 425 – 442.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。

合格投資者聲明(míng)

FF3 們背後的(de)資産定價理(lǐ)論