Toward a better factor model

發布時(shí)間：2021-03-30 | 來(lái)源: 川總寫量化(huà)

作者：石川

摘要：當傳統檢驗無法有效比較多(duō)因子模型時(shí)，一些新方法的(de)誕生彌補了(le)它的(de)不足，讓人(rén)們朝著(zhe)找到真正意義上更優的(de)多(duō)因子模型又邁進了(le)一步。

1 實證中的(de)困惑

你是否在比較不同的(de)多(duō)因子模型時(shí)因爲下(xià)面這(zhè)些自相矛盾的(de)結果而倍感困惑？

1. 往多(duō)因子模型中加入一個(gè)額外的(de)因子，但是 test assets 的(de) pricing errors 卻增加了(le)。

2. 一個(gè)多(duō)因子模型能夠解釋其他(tā) test assets 的(de)超額收益，但是卻對(duì)構造因子的(de) sorted portfolios 的(de)超額收益無能爲力。

3. 對(duì)因子 mimicking portfolio 的(de)改造或新因子的(de)加入确實提升了(le)多(duō)因子模型的(de)定價能力，但這(zhè)些因子卻有更高(gāo)的(de)換手率和(hé)更昂貴的(de)交易成本。

……

你并不孤單，這(zhè)些是人(rén)們在實證資産定價或多(duō)因子模型研究中會碰上的(de)問題。在諸多(duō)情景中，上述問題 1 大(dà)概是最普遍的(de)，比如在美(měi)股中，當給使用(yòng)市值和(hé) accruals 雙重獨立排序構造的(de) test assets 定價時(shí)，Fama and French (1993) 三因子模型竟然優于 Fama and French (2015) 五因子模型，盡管後者比前者多(duō)了(le)兩個(gè)解釋變量。

我們就從問題 1 說起。當檢驗多(duō)因子模型時(shí)，最常見的(de)做(zuò)法是用(yòng)一組 test assets 分(fēn)别對(duì)多(duō)因子模型回歸，得(de)到每個(gè) test asset 的(de) pricing error（即 $\alpha$ ）。有了(le)這(zhè)些 $\alpha$ ，可(kě)以考慮它們絕對(duì)值的(de)均值，也(yě)可(kě)以用(yòng) Gibbons, Ross and Shanken (1989) test（GRS test）檢驗所有 pricing errors 是否聯合爲零。如果在模型 A 下(xià)，test assets 的(de) pricing errors 比在模型 B 下(xià)更小，人(rén)們通(tōng)常就會認爲模型 A 優于模型 B。

從上述描述可(kě)以看出，這(zhè)種方法很大(dà)程度依賴于選擇了(le)哪些 test assets 來(lái)檢驗模型。由于它們在回歸模型中是被解釋變量，因此 Eugene Fama 把這(zhè)種檢驗方法稱爲 Left-Hand-Side (LHS) approach（Fama and French (2018)）。

LHS approach 至少存在兩個(gè)問題。第一，模型比較的(de)結果是 test assets specific。當人(rén)們使用(yòng)不同 test assets 時(shí)，檢驗結果可(kě)能出現逆轉；而且也(yě)無法保證不同多(duō)因子模型的(de)發明(míng)者不去選擇最适合自己模型的(de) test assets（data snooping）。而第二個(gè)問題，正如上面的(de)例子所示，就是當模型中加入更多(duō)因子後，test assets 的(de) pricing errors 不降反升，導緻人(rén)們得(de)出錯誤的(de)結論。

若某個(gè)模型中的(de)因子是另一個(gè)模型因子的(de)子集，它們被稱爲 nested models，例如通(tōng)過往模型 A 中加入新的(de)因子而構造出模型 B 時(shí)，模型 A 和(hé) B 就是 nested models；如果模型中有非重合的(de)因子，那麽它們被稱爲 non-nested models。對(duì)于 nested models，更多(duō)的(de)因子反而造成 test assets 的(de) pricing errors 上升，則著(zhe)實令人(rén)困惑。以下(xià)通(tōng)過一個(gè)簡單的(de)數學模型來(lái)解釋背後的(de)原因。

假設存在模型 A 和(hé) B，前者中有因子 1（記爲 $f_1$ ），後者中包括 $f_1$ 和(hé)另一個(gè)因子 2（記爲 $f_2$ ），令 $R$ 表示 test asset 的(de)超額收益。當使用(yòng)模型 B 時(shí)有：

$R = \alpha_R + \beta_1 f_1 + \beta_2 f_2 + \varepsilon~~~~~ (1)$

其中 $\alpha_R$ 表示 test asset 在模型 B 下(xià)的(de) pricing error。類似的(de)，當使用(yòng)模型 A 時(shí)有：

$R = \alpha_{R1} + b f_1 + e ~~~~~ (2)$

其中 $\alpha_{R1}$ 爲 test asset 在模型 A 下(xià)的(de) pricing error。另一方面，假設因子 $f_2$ 和(hé) $f_1$ 之間滿足如下(xià)回歸模型：

$f_2 = \alpha_{21} + d f_1 + u ~~~~~ (3)$

這(zhè)個(gè)式子意味著(zhe)将因子 2 視爲 test asset 并使用(yòng)模型 A 對(duì)其定價，因此 $\alpha_{21}$ 爲因子 2 在模型 A 下(xià)的(de) pricing error。将 (3) 代入 (1) 有：

$\begin{array}{rll} R &=& \alpha_R + \beta_1 f_1 + \beta_2(\alpha_{21}+d f_1+u)+\varepsilon\\ &=&(\alpha_r+\beta_2\alpha_{21})+(\beta_1+\beta_2d)f_1+(\beta_2 u+\varepsilon) ~~~~~ (4) \end{array}$

比較 (4) 和(hé) (2) 可(kě)知：

$\alpha_{R1} = \alpha_R + \beta_2\alpha_{21}$

即test asset 在兩個(gè)模型下(xià)定價誤差，即 $\alpha_{R1}$ 和(hé) $\alpha_R$ ，的(de)差異取決于 $\beta_2\alpha_{21}$ 的(de)大(dà)小。此外，讓情況變得(de)更加 tricky 的(de)是，pricing error 本身可(kě)正可(kě)負，而當人(rén)們說“更低”時(shí)意味著(zhe)它的(de)絕對(duì)值更接近零。所以，通(tōng)過 test asset 的(de) pricing error 來(lái)比較上述兩個(gè)模型，取決于 $\alpha_{R1}$ 和(hé) $\alpha_{R}$ 這(zhè)二者本身的(de)大(dà)小和(hé)正負号，以及 $\beta_2\alpha_{21}$ 這(zhè)一項的(de)大(dà)小和(hé)正負号。因此，在一些情況下(xià)，LHS approach 會出現加入更多(duō)因子，pricing errors 反倒增大(dà)。

既然問題已經清楚了(le)，那麽爲了(le)解決它是應該找更合理(lǐ)的(de) test assets，還(hái)是找處理(lǐ) pricing errors（ $\alpha$ ）的(de)更好的(de)檢驗方法呢(ne)？有大(dà)佬說“都不是”。

2 A Right-Hand-Side Approach

對(duì)于上述問題，Barillas and Shanken (2017) 給出了(le)答(dá)案。該文以 Which alpha? 爲題，給出了(le)一個(gè)簡單卻又頗讓人(rén)驚訝的(de)結論：test assets 對(duì)于比較多(duō)因子模型來(lái)說是無關的(de)。OK，更嚴謹的(de)話(huà)，應該說如果模型中隻考慮 traded factors，那麽 test assets 是無關的(de)。如果有 non-traded factors，則它們的(de) factor mimicking portfolios 需要通(tōng)過 test assets 構造，因此是有關的(de)。不過爲了(le)本文的(de)介紹，我們就考慮簡單的(de)情況。Barillas and Shanken (2017) 的(de)結論對(duì) nested assets 和(hé) non-nested assets 都成立。

該文的(de)核心出發點是，當比較多(duō)因子模型時(shí)，除了(le) test assets 之外，也(yě)應該檢驗模型能否解釋彼此的(de)因子：Our central insight in this context is a simple one — that models should be compared in terms of their ability to price all returns, both test assets and traded factors. 舉例來(lái)說，假如模型 A 和(hé) B 各自包含因子 1，2，3 和(hé)因子 1，4，5。在比較它們時(shí)，Barillas and Shanken (2017) 主張把這(zhè)兩個(gè)模型包含的(de)全部 5 個(gè)因子也(yě)一同視作 test assets，它們将和(hé)之前額外選定的(de) test assets 一起，被用(yòng)來(lái)檢驗模型 A 和(hé) B 的(de)定價能力。當把所有待比較模型的(de)因子加入 test assets 之後，“神奇”的(de)事情發生了(le)。對(duì)模型 $i$ 下(xià)的(de)一組定價誤差 $\alpha_i$ ，令 $\Sigma_i$ 爲殘差的(de)協方差矩陣，則 $\alpha_i^\prime\Sigma_i^{-1}\alpha_i$ 就是這(zhè)些 $\alpha_i$ 構造的(de)最大(dà)夏普率平方（max squared Sharpe ratio），記爲 $SR^2(\alpha_i)$ 。Gibbons, Ross and Shanken (1989) 證明(míng)了(le) $SR^2(\alpha_i)$ 等于由模型中所有因子 + test assets 共同構造的(de)最大(dà)夏普率平方與僅使用(yòng)全部因子構造的(de)最大(dà)夏普率平方之差。

假設比較兩個(gè)模型，它們的(de)因子記爲 $f_1$ 和(hé) $f_2$ ，一組額外 test assets 的(de)超額收益爲記爲 $R$ （其中 $f_1$ 、 $f_2$ 、 $R$ 都代表多(duō)個(gè)因子和(hé) test assets）。根據 Barillas and Shanken (2017) 的(de)觀點， $f_1$ 、 $f_2$ 以及 $R$ 應該通(tōng)通(tōng)被當作 test assets 檢驗兩個(gè)模型（顯然模型 1 能夠解釋 $f_1$ ；模型 2 能夠解釋 $f_2$ ）。在這(zhè)種設定下(xià)，模型 1 的(de)定價能力表示爲：

$SR^2(\alpha_1) = SR^2(f_1, f_2, R) – SR^2(f_1)$

同理(lǐ)，模型 2 的(de)定價能力表示爲：

$SR^2(\alpha_2) = SR^2(f_2, f_1, R) – SR^2(f_2)$

當模型 1 優于模型 2 時(shí)，應該有 $SR^2(\alpha_1) < SR^2(\alpha_2)$ 。這(zhè)個(gè)公式的(de)直觀理(lǐ)解是，相較于模型 2 來(lái)說，模型 1 本身的(de)因子 span 而成的(de) tangency portfolio 的(de)夏普率的(de)平方更大(dà)，加入其他(tā) test assets（ $f_2$ 和(hé) $R$ ）之後的(de)提升更小（即 $SR^2(\alpha_1)$ 更小）。簡單的(de)代數運算(suàn)可(kě)知：

$SR^2(f_1, f_2, R) – SR^2(f_1) < SR^2(f_2, f_1, R) – SR^2(f_2) ~~~~~ (5)$

由于額外的(de) test assets 同時(shí)出現在上式左右兩側，它對(duì)于夏普率平方的(de)增量貢獻是一樣的(de)，因此可(kě)以被消去，(5) 變爲：

$SR^2(f_1, f_2) – SR^2(f_1) < SR^2(f_2, f_1) – SR^2(f_2) ~~~~~ (6)$

這(zhè)就是爲什(shén)麽當把所有因子也(yě)作爲 test assets 後，額外的(de) test assets 對(duì)于比較模型來(lái)說就無關了(le)。上式中的(de)關系正是 Barillas and Shanken (2017) 希望傳達出來(lái)的(de)最重要的(de)觀點。

It turns out that test assets tell us nothing about model comparison beyond what we learn by examining the extent to which each model prices the factors in the other models. So the test assets can be ignored for this purpose. This is the main message of our paper.

對(duì) (6) 進行化(huà)簡，最終得(de)到如下(xià)結論，即如果模型 1 優于模型 2，則應該有：

$SR^2(f_1) >SR^2(f_2) ~~~~~ (7)$

即由模型 1 的(de)因子 $f_1$ 構造的(de)最大(dà)夏普率平方高(gāo)于由模型 2 的(de)因子 $f_2$ 構造的(de)最大(dà)夏普率平方。從 (7) 出發可(kě)知，當比較不同模型時(shí)，隻需考察它們各自的(de)因子能夠 span 出來(lái)的(de) tangency portfolio 的(de)夏普率平方即可(kě)。由于這(zhè)個(gè)檢驗僅考慮因子而因子出現在多(duō)因子模型的(de)右側，因此這(zhè)個(gè)方法又被稱爲 Right-Hand-Side (RHS) approach。

Barillas and Shanken (2017) 對(duì)這(zhè)個(gè)方法的(de) implication 以及它在檢驗 nested 和(hé) non-nested models 時(shí)的(de)作用(yòng)進行了(le)系統的(de)討(tǎo)論。Fama and French (2018) 也(yě)對(duì)這(zhè)個(gè)方法進行了(le)系統的(de)實證研究。使用(yòng) RHS approach 代替 LHS approach 不會遇到本文開篇的(de)問題 1。在某個(gè)模型中加入額外的(de)因子時(shí)，如果該因子不能被現有因子 span，則它的(de)加入一定會提升夏普率平方，從而讓人(rén)得(de)出包含更多(duō)因子的(de)新模型優于老模型這(zhè)樣符合直覺的(de)結論。一般來(lái)說，當越來(lái)越多(duō)因子被加入到模型中，它的(de) ex-post 最大(dà)夏普率平方總能提升。然而，從簡約性（The Law of Parsimony，見《因子投資：方法與實踐》的(de) 4.4 節：多(duō)因子模型的(de)簡約性）的(de)角度來(lái)考慮也(yě)有必要限制模型中因子的(de)個(gè)數。但無論如何，Barillas and Shanken (2017) 提出的(de) RHS approach 還(hái)是給檢驗多(duō)因子模型提出了(le)新思路。爲了(le)得(de)到更好的(de)多(duō)因子模型，應同時(shí)考慮 LHS 和(hé) RHS 兩種方法。

當然，以最大(dà)化(huà) ex-post 夏普率平方爲目标評價因子模型也(yě)絕非沒有弊端。比如通(tōng)過選擇奇葩的(de)因子、改變因子的(de)構造或者使用(yòng)頻(pín)率更高(gāo)的(de)數據（Fama-French 三/五因子模型用(yòng)年報數據吃(chī)了(le)這(zhè)方面的(de)虧），就可(kě)以輕松提升最大(dà)夏普率平方。但是，這(zhè)些做(zuò)法會帶來(lái)新問題，處理(lǐ)不好也(yě)會讓人(rén)們離 “更好的(de)多(duō)因子模型”越來(lái)越遠(yuǎn)。不過我們先賣個(gè)關子，等到本文第 4 節在討(tǎo)論。

3 A Specification Test

在這(zhè)一節我想討(tǎo)論一下(xià)本文開篇的(de)問題 2。目前學術界提出的(de)所有主流多(duō)因子模型（見《因子投資：方法與實踐》4.1 節的(de)詳細介紹），它們在構造因子投資組合時(shí)，均是沿用(yòng)了(le) Fama and French (1993) 的(de)方法，即采用(yòng)市值和(hé)另一個(gè)變量（如 HML 中的(de) BM）進行雙重排序（唯一的(de)例外是 Carhart (1997) 的(de)動量因子），将所有股票(piào)劃分(fēn)成若幹個(gè)組合，然後利用(yòng)這(zhè)些組合構造最後的(de)因子投資組合。對(duì)于因子來(lái)說，這(zhè)些用(yòng)來(lái)構造改因子的(de)基礎組合可(kě)以被稱爲 basis portfolios。

當人(rén)們檢驗和(hé)比較多(duō)因子模型時(shí)，LHS approach 關注的(de)是其解釋 test assets 的(de)能力，而上一節介紹的(de) RHS approach 雖然在 test assets 中也(yě)考慮了(le)因子，但依然沒有考慮不同因子背後的(de) basis portfolios。如果一個(gè)多(duō)因子模型是優秀的(de)，那麽合理(lǐ)的(de)預期是它至少應該能解釋自己的(de) basis portfolios。如果它在解釋其他(tā)資産方面呼風喚雨(yǔ)，卻對(duì)自己的(de) basis portfolios 無能爲力，那麽就難以令人(rén)信服。不過，無論是學界還(hái)是業界，似乎很少有人(rén)關注這(zhè)些 basis portfolios，也(yě)沒有專門的(de)檢驗方法。

直到 Liao and Liu (2020) 出現。這(zhè)是一篇雖然尚未發表，但我個(gè)人(rén)非常喜歡的(de) working paper。它針對(duì)多(duō)因子模型檢驗中的(de)截面回歸方法（見《多(duō)因子模型的(de)回歸檢驗》或《因子投資：方法與實踐》的(de) 2.2.2 節）提出了(le)全新的(de) two-pass estimator。概括的(de)說，該方法在廣義矩估計（GMM，見《Generalized Method of Moments》）框架下(xià)通(tōng)過矩條件研究了(le) two-pass estimator，并找到了(le)一個(gè)最優的(de)權重矩陣，使得(de)被估計參數的(de)方差最小，進而保證了(le)估計量的(de) efficiency。因此該估計量也(yě)被稱爲 optimal cross-sectional regression (OCSR) estimator。

一般來(lái)說，two-pass 截面回歸檢驗可(kě)以被表示成以下(xià)矩條件（這(zhè)裏的(de)因子 $f_t$ 可(kě)以使 traded 或 non-traded factors）：

$\begin{array}{rll} \mbox{E}[f_t-\mu_f]&=&0\\ \mbox{E}[(R_{i,t}-(f_t-\mu_f)^\prime\beta_i)(f_t-\mu_f)]&=&0\\ \mbox{E}[R_{i,t}-\alpha_i-\gamma_0-\gamma_1^\prime\beta_i-\gamma_2^\prime Z_{i,t}]&=&0 \end{array}$

其中前兩組矩條件對(duì)應 two-pass regression 中的(de)第一步，即估計資産對(duì)因子的(de)暴露；第三組矩條件則對(duì)應 two-pass regression 中的(de)第二步，即截面回歸估計因子溢價。除了(le)上述矩條件之外，Liao and Liu (2020) 還(hái)在框架中注入了(le)一個(gè)約束，即允許一組資産在待檢驗的(de)模型下(xià)的(de) pricing error（ $\alpha$ ）爲零（相當于減少了(le)待估計參數的(de)個(gè)數）：

$\alpha_i = 0~~\mbox{for any}~~i\in\mathcal{I}_0$

和(hé) GMM 同時(shí)使用(yòng)所有矩條件進行估計不同，該方法本質上還(hái)是傳承了(le) two-pass regression。因此雖然問題被表述爲矩條件的(de)形式，但在實際求解時(shí)，前兩組矩條件和(hé)第三組矩條件以及約束是分(fēn)開的(de)。首先利用(yòng)前兩組矩條件估計出因子暴露，然後再利用(yòng)它們作爲參數，通(tōng)過第三組矩條件和(hé)約束來(lái)估計因子溢價和(hé)資産的(de) pricing error。

在傳統的(de) GLS/OLS 中，它們的(de)差異源于截面回歸估計因子溢價時(shí)，N 個(gè)資産的(de)權重矩陣（比如 OLS 就是個(gè)單位陣）。而 OCSR 和(hé) GLS/OLS 最大(dà)的(de)差異就是權重矩陣的(de)選擇。經過一系列計量經濟學推導，Liao and Liu (2020) 給出了(le)最優的(de)權重矩陣，使得(de)他(tā)們的(de) estimator 擁有和(hé) GMM 一樣的(de)優秀特性，但卻遠(yuǎn)比直接求解 GMM 簡單的(de)多(duō)。這(zhè)也(yě)正是該方法最吸引人(rén)的(de)地方。實證結果顯示，該方法比傳統的(de) OLS/GLS 在估計因子溢價方面都有優勢。

OK! 說了(le)半天你也(yě)許要問，這(zhè)和(hé)本節一開始提到的(de) basis portfolios 有關系嗎？在 Liao and Liu (2020) 一文中，除了(le)提出 OCSR estimator 之外，兩位作者也(yě)給出了(le)一個(gè) specification test，這(zhè)就和(hé) basis portfolios 有關了(le)。前文已經說了(le)，Liao and Liu (2020) 的(de)框架允許一組資産在多(duō)因子模型下(xià)的(de) pricing errors 是零；而這(zhè)個(gè) specification test 就是用(yòng)來(lái)檢驗這(zhè)組資産的(de) pricing errors 到底是否爲零，即

$H_0: E[R_{i,t}-\gamma_0-\gamma_1^\prime\beta_i-\gamma_2^\prime Z_{i,t}]=0, i\in \mathcal{I}_0$

放在我們的(de)場(chǎng)景下(xià)，隻需要把該模型的(de) basis portfolios 和(hé)其他(tā)資産一起作爲 test assets，并假設 basis portfolios 滿足 pricing errors 爲零的(de)約束。在求出最優權重矩陣之後，利用(yòng) specification test 就可(kě)以檢驗 basis portfolios 是否滿足該約束。如果原假設被拒絕，則該模型無法爲 basis portfolios 定價。

Liao and Liu (2020) 依照(zhào)上述思路比較了(le)近年來(lái)最引人(rén)關注的(de)兩個(gè)模型，Fama and French (2015) 五因子模型（FF5）和(hé) Hou, Xue and Zhang (2015) 的(de) q-factor model（曆史背景見《從 Factor Zoo 到 Factor War，實證資産定價走向何方？》）。Specification test 結果顯示，FF5 的(de) basis portfolios 的(de)檢驗結果 p-value 爲 0.121（無法拒絕原假設），而 q-factor model 的(de) basis portfolios 的(de)檢驗結果 p-value 爲 0.000（可(kě)以在任何常見的(de)顯著性水(shuǐ)平下(xià)安全的(de)拒絕原假設）。因此，FF5 可(kě)以解釋自己的(de) basis portfolios，而 q-factor model 卻不能。

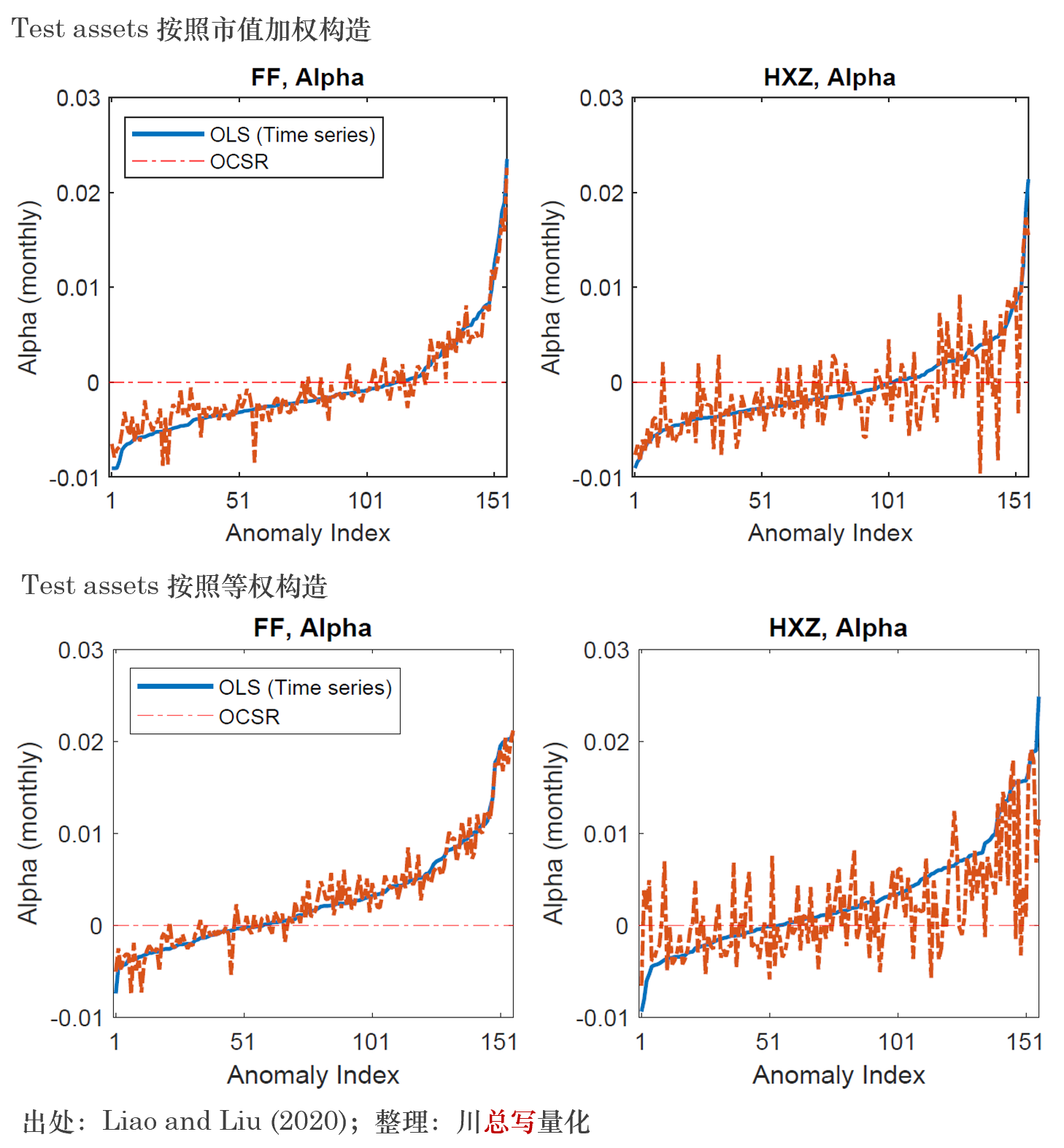
除此之外，針對(duì) FF5 和(hé) q-factor model 均是通(tōng)過 LHS approach（時(shí)序回歸檢驗）來(lái)評估它們的(de)定價能力，Liao and Liu (2020) 也(yě)使用(yòng)他(tā)們提出的(de) OCSR estimator 進行了(le)比較。對(duì)于一個(gè)優秀的(de)多(duō)因子模型來(lái)說，雖然時(shí)序回歸檢驗和(hé)截面回歸檢驗有所差異，但我們依然可(kě)以預期 test assets 在模型下(xià)的(de) pricing errors 在兩種方法下(xià)式接近的(de)，否則該模型就不那麽靠譜。結果嘛，再一次讓人(rén)震驚：FF5“完勝”q-factor model。

根據上圖所示（無論是市值加權還(hái)是等權構造 test assets），對(duì)于考慮的(de) 156 個(gè) test assets，當使用(yòng) FF5 爲模型時(shí)，它們在兩種方法下(xià)的(de) pricing errors 十分(fēn)一緻；而在 q-factor model 下(xià)卻表現出來(lái)很大(dà)的(de)差異。綜合這(zhè)個(gè)結果和(hé)前述 specification test，我們可(kě)以得(de)出初步的(de)結論：q-factor model 可(kě)能存在模型設定偏誤。

雖然既有 LHS approach 的(de)實證結果一邊倒的(de)支持了(le) q-factor model 相對(duì)于 FF5 的(de)優越性（Hou et al. (2019)），但上述實證結果無疑爲人(rén)們重新評判 FF5 和(hé) q-factor model 提供了(le)新的(de)依據。頗有意思的(de)是，FF 曾在評價 q-factor model 時(shí)提到：More important, they (HXZ) are primarily concerned with explaining the returns associated with anomaly variables not used to construct their factors. 通(tōng)過 Liao and Liu (2020) 的(de) specification test，上述觀點得(de)到了(le)驗證。一個(gè)多(duō)因子模型至少應能夠解釋自己的(de) basis portfolios，這(zhè)個(gè)條件應該成爲尋找更好的(de)模型時(shí)的(de)必要條件。

4 展望

在總結本文和(hé)展望未來(lái)之前，先來(lái)回應一下(xià)第二節最後提出的(de)問題，即以最大(dà)化(huà) ex-post 夏普率平方爲目标構造模型的(de)弊端，它也(yě)和(hé)本文開篇的(de)問題 3 息息相關。無論是研究因子還(hái)是比較多(duō)因子模型，以最大(dà)化(huà) ex-post 夏普率平方爲目标會帶來(lái)兩個(gè)問題：（1）因子研究本末倒置，數據先行；（2）因子的(de)理(lǐ)論表現越來(lái)越脫離實際。

對(duì)于第一個(gè)問題，一個(gè)驚人(rén)的(de)例子是在美(měi)股上針對(duì)低波動股票(piào)構造的(de)反轉因子，它自己的(de) ex-post 夏普率平方是 Fama-French 三因子模型的(de) 9 倍；五因子模型的(de) 4 倍。但顯然，沒有人(rén)會在 FF3/5 和(hé)這(zhè)個(gè)反轉因子之間選擇後者。這(zhè)個(gè)例子說明(míng)，我們在追求更好的(de) tangency portfolio 時(shí)，應該時(shí)刻注意檢查因子本身是不是有邏輯，而非單純依靠數據。Fama and French (2018) 曾說，實證資産定價中的(de)因子是來(lái)自對(duì)曆史平均收益率中某種模式的(de)發掘。一旦因子背後缺乏理(lǐ)論支撐，那麽因子研究就會退化(huà)成以提升 ex-post tangency portfolio 爲目标的(de)數據挖掘。（這(zhè)也(yě)是 Fama 對(duì)動量因子始終持謹慎态度的(de)原因。）對(duì)于第二個(gè)問題，金融學作爲理(lǐ)論緊密聯系實際的(de)一門學科，它要求理(lǐ)論能夠很好的(de)指導實際。這(zhè)意味著(zhe)在比較多(duō)因子模型時(shí)，不應（僅）考慮因子 on paper 的(de)收益率以及通(tōng)過這(zhè)些收益率計算(suàn)出的(de)夏普率，而是要考慮投資者實際可(kě)交易出來(lái)的(de)因子的(de)收益率（即扣掉交易成本之後）。

越來(lái)越多(duō)實證結果顯示，使用(yòng)更高(gāo)頻(pín)率的(de)變量或者使用(yòng)一些不走尋常路的(de)構造方法均可(kě)以提升因子 on paper 收益率，然而這(zhè)些提升都是以更高(gāo)的(de)換手率和(hé)交易成本爲代價。仍以 FF5 和(hé) q-factor model 爲例，它們二者都包含盈利因子，然而 FF5 使用(yòng)年度數據而 q-factor model 使用(yòng)季度數據；且 q-factor model 使用(yòng)三重排序來(lái)構造因子。這(zhè)些差異導緻了(le) q-factor model 中盈利因子的(de) on paper 收益率要比 FF5 的(de)版本高(gāo)的(de)多(duō)。最終，以最大(dà)化(huà)夏普率平方來(lái)看，q-factor model 也(yě)優于 FF5。

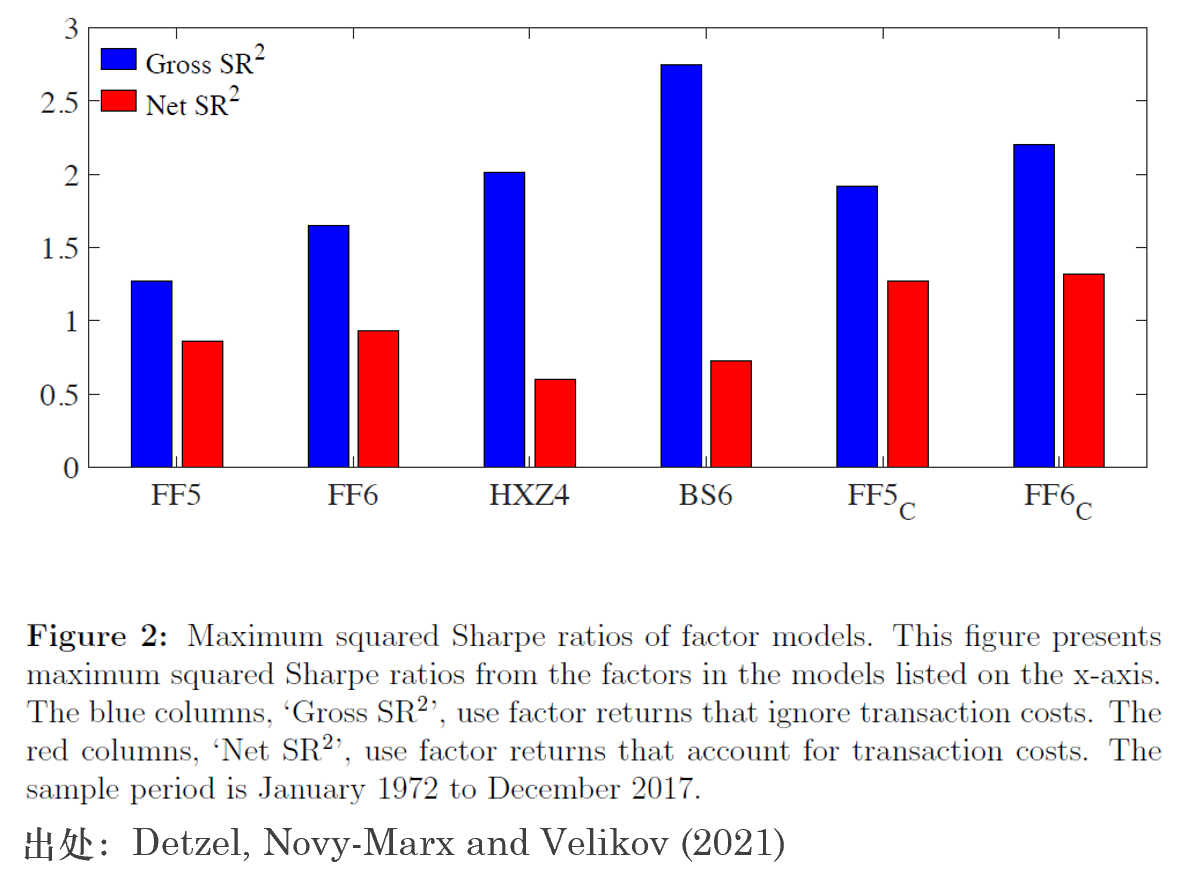
但是考慮了(le)交易成本又會怎樣呢(ne)？Detzel, Novy-Marx and Velikov (2021) 系統比較了(le)不同多(duō)因子模型在扣除交易成本後，因子都能實現的(de)最大(dà)化(huà)夏普率平方（前文《Factor War 外傳》曾介紹過該文，當時(shí)該文還(hái)沒有被挂到 SSRN，如今已經可(kě)以下(xià)載）。結果如下(xià)圖所示，一旦考慮因子實際的(de)收益率，模型比較的(de)結果就可(kě)能發生反轉。

說完了(le)這(zhè)兩個(gè)問題，最後來(lái)總結一下(xià)。近年來(lái)，學術界以尋找更好的(de)多(duō)因子模型爲目标做(zuò)出了(le)很多(duō)有益的(de)嘗試。就我個(gè)人(rén)的(de)看法，一個(gè)可(kě)參考的(de) protocol 也(yě)慢(màn)慢(màn)的(de)浮出了(le)水(shuǐ)面：

1. 多(duō)因子模型中的(de)每個(gè)因子都應該有邏輯；

2. 模型應該有 inner consistency，能夠解釋其 basis portfolios 是必要條件；

3. 比較模型時(shí)，同時(shí)考慮 LHS 和(hé) RHS 方法，當二者産生分(fēn)歧時(shí)應分(fēn)析背後的(de)原因；

4. 從資産定價理(lǐ)論來(lái)說，因子應該能 span 出 tangency portfolio，但這(zhè)種嘗試不應僅停留在理(lǐ)論上，應該給予實際可(kě)交易出的(de)收益率足夠的(de)重視。

以此爲指引，有理(lǐ)由相信我們終将會遇到更好的(de)多(duō)因子模型。

參考文獻

Barillas, F. and J. Shanken (2017). Which alpha? Review of Financial Studies 30(4), 1316 – 1338.

Carhart, M. M. (1997). On persistence in mutual fund performance. Journal of Finance 52(1), 57 – 82.

Detzel, A., R. Novy-Marx, and M. Velikov (2021). Model selection with transaction costs. Working paper.

Fama, E. F. and K. R. French (1993). Common risk factors in the returns on stocks and bonds. Journal of Financial Economics 33(1), 3 – 56.

Fama, E. F. and K. R. French (2015). A five-factor asset pricing model. Journal of Financial Economics 116(1), 1 – 22.

Fama, E. F. and K. R. French (2018). Choosing factors. Journal of Financial Economics 128(2), 234 – 252.

Gibbons, M. R., S. A. Ross, and J. Shanken (1989). A test of the efficiency of a given portfolio. Econometrica 57(5), 1121 – 1152.

Hou, K., H. Mo, C. Xue, and L. Zhang (2019). Which factors? Review of Finance 21(1), 1 – 35.

Hou, K., C. Xue, and L. Zhang (2015). Digesting anomalies: An investment approach. Review of Financial Studies 28(3), 650 – 705.

Liao, Z. and Y. Liu (2020). Optimal cross-sectional regression. Working paper.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。

合格投資者聲明(míng)

Toward a better factor model