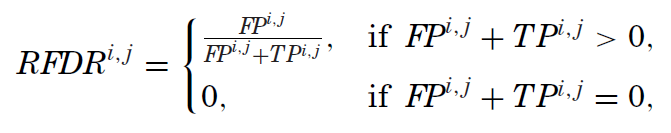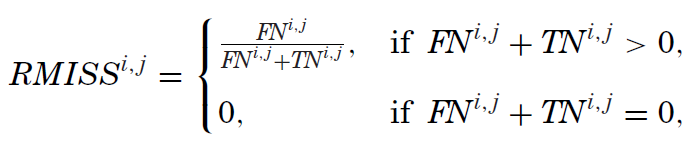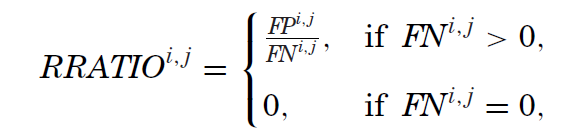出色不如走運 (V)?
發布時(shí)間:2021-02-03 | 來(lái)源: 川總寫量化(huà)
作者:石川
摘要:貝葉斯思維和(hé)對(duì) Type II error rate 的(de)考量讓多(duō)重假設檢驗方法上升到了(le)新的(de)高(gāo)度。
1 引言
如果要說 2020 年令人(rén)印象深刻的(de)金融學論文,Harvey and Liu (2020) 一定會有一席之地。在這(zhè)篇題爲 False (and missed) discoveries in financial economics、發表于 Journal of Finance 的(de)文章(zhāng)中,二位作者将 multiple hypothesis testing(多(duō)重假設檢驗)方法論提升到了(le)新高(gāo)度。
如今再談到多(duō)重假設檢驗,公衆号的(de)小夥伴一定不再陌生了(le)。《出色不如走運》系列的(de)前幾篇文章(zhāng)均圍繞這(zhè)個(gè)話(huà)題進行了(le)探討(tǎo)。在學術論文方面,Harvey, Liu, and Saretto (2020) 一文對(duì)常見的(de)方法進行了(le)總結,而《出色不如走運》系列的(de)“番外篇”《常見多(duō)重檢驗方法及其實證》也(yě)參照(zhào)該文針對(duì) A 股對(duì)其中一些方法進行了(le)實證。
概括來(lái)說,傳統的(de)多(duō)重假設檢驗方法均可(kě)以歸納到“正交化(huà)” + “bootstrap”兩個(gè)技術的(de)綜合運用(yòng)。以挖掘股票(piào)市場(chǎng)異象爲情景來(lái)說,其中“正交化(huà)”的(de)作用(yòng)是在樣本内剔除每個(gè)異象的(de)超額收益;“bootstrap”則是在正交化(huà)後的(de)基礎上通(tōng)過重采樣更多(duō)的(de)數據,以此獲得(de)僅由運氣造成的(de)異象超額收益顯著性(t-statistic)的(de)分(fēn)布。
在得(de)到由運氣造成的(de)顯著性(t-statistic)的(de)分(fēn)布後,這(zhè)些方法往往以控制事先約定的(de) Type I error rate(false discovery rate),例如常見的(de) 5%,來(lái)選定 t-statistic 的(de)阈值,并以此确定哪些異象能夠獲得(de)顯著的(de)超額收益。
傳統方法雖然簡單易用(yòng),但是存在兩個(gè)問題:
1. 在“正交化(huà)”的(de)過程中,往往會對(duì)所有異象都做(zuò)“正交化(huà)”處理(lǐ)(原假設爲異象超額收益爲零)。然在現實中,這(zhè)種處理(lǐ)方法忽視了(le)先驗的(de)作用(yòng)。對(duì)于待檢驗的(de)諸多(duō)異象,人(rén)們可(kě)能根據金融學先驗認爲其中一定比例的(de)異象的(de)超額收益是顯著的(de),但傳統的(de)方法并不能利用(yòng)這(zhè)種先驗。
2. t-statistic 阈值是通(tōng)過事先約定的(de) Type I error rate 确定的(de),而不去考慮 Type I 和(hé) Type II 兩類錯誤的(de) trade-off。這(zhè)麽做(zuò)的(de)結果是,傳統多(duō)重假設檢驗方法的(de) Type II error rate 往往很高(gāo),power (= 1 – Type II error rate) 往往很低。舉個(gè)極端的(de)例子,假設某個(gè)算(suàn)法把所有原假設都接受了(le),那麽它也(yě)就沒能發現任何真正的(de)異象(power = 0)。
對(duì)研究異象來(lái)說,Type II error 意味著(zhe)異象本身能夠獲得(de)超額收益(原假設爲假),但是檢驗并沒有拒絕其原假設,因此錯失了(le)真正的(de)異象。
盡管如此,常見方法僅僅關心 Type I error rate 也(yě)實在是無奈之舉。這(zhè)是因爲哪怕對(duì)于單一假設檢驗,計算(suàn) Type II error rate 都并不容易,更不用(yòng)說多(duō)重假設檢驗問題。如果想要計算(suàn) Type II error rate,就必須知道備擇假設下(xià)參數的(de)取值(本文附錄部分(fēn)引用(yòng)了(le) Wikipedia 的(de)例子說明(míng)如何在單一假設檢驗下(xià)計算(suàn) Type II error rate)。但顯然,對(duì)于成百上千個(gè)異象來(lái)說,想要遍曆它們備擇假設下(xià)的(de)預期超額收益不切實際。這(zhè)個(gè)巨大(dà)的(de)障礙使得(de)人(rén)們難以将單一檢驗中計算(suàn) Type II error rate 的(de)方法複制到多(duō)重假設檢驗問題中。
除了(le)分(fēn)析的(de)難度,還(hái)有另一個(gè)原因是人(rén)們在過去通(tōng)常認爲 Type II error 的(de)影(yǐng)響不如 Type I error 的(de)影(yǐng)響大(dà)。以大(dà)幅提升分(fēn)析難度爲代價,換來(lái)的(de)邊際期望收益卻有限,似乎有些得(de)不償失。不過,這(zhè)種看法也(yě)逐漸在轉變。在 α 越來(lái)越稀缺的(de)當下(xià),Type II error 的(de)成本越來(lái)越高(gāo),讓人(rén)開始重視兩類錯誤之間的(de)取舍。
在這(zhè)種背景下(xià),Harvey and Liu (2020) 提出了(le)一個(gè)基于雙重 bootstrap 的(de)多(duō)重假設檢驗框架,同時(shí)解決了(le)上述兩個(gè)問題。
2 Harvey and Liu (2020)
假設一共有 N 個(gè)異象,原始數據爲 T × N 階異象收益率序列矩陣(記爲 X_0),其中 T 爲期數。這(zhè)一步的(de)設定和(hé)傳統多(duō)重假設檢驗方法無異,但是 Harvey and Liu (2020) 的(de)不同之處是通(tōng)過參數 p_0 來(lái)控制真實異象的(de)比例。人(rén)們可(kě)以根據自身的(de)經驗來(lái)選擇 p_0 的(de)取值,它是貝葉斯思維的(de)體現。
當選定 p_0 後,一個(gè)自然的(de)想法是在全部 N 個(gè)異象中收益率均值的(de) t-statistic 最高(gāo)的(de) N × p_0 個(gè)是真實的(de)。但是我們手頭這(zhè) N 個(gè)異象的(de)收益率序列也(yě)是來(lái)自未知總體。考慮到 sampling uncertainty,它們中最高(gāo)的(de) N × p_0 個(gè)也(yě)并非就一定都是真的(de)。爲了(le)解決這(zhè)個(gè)問題 Harvey and Liu (2020) 進行了(le)第一輪 bootstrap。
通(tōng)過對(duì) X_0 進行 bootstrap sampling 得(de)到矩陣 X_i(下(xià)标 i 表示第 i 個(gè) bootstrap 樣本)。使用(yòng) X_i 中的(de)收益率序列計算(suàn) N 個(gè)異象的(de) t-statistics,并選出最高(gāo)的(de) N × p_0 個(gè)。在原始矩陣 X_0 中,将這(zhè)些異象的(de)收益率均值替換爲它們在 X_i 中的(de)均值,并把 X_0 中剩餘那些異象的(de)收益率做(zuò)去均值處理(lǐ),以此構造出矩陣 Y_i。
經過上述構造後,每次對(duì) X_0 進行一次 bootstrap sampling,都會得(de)到一個(gè) Y_i,其中有 N × p_0 個(gè)異象的(de)超額收益均值非零(顯著的(de)),剩餘 N × (1 - p_0) 個(gè)異象的(de)超額收益均值爲零(不顯著)。
在上述過程中,對(duì)剩餘 N × (1 - p_0) 個(gè)異象時(shí)序收益率的(de)去均值操作體現了(le)“正交化(huà)”的(de)思想;而對(duì) N × p_0 個(gè)異象保留收益率均值則源于先驗。此外這(zhè)種操作通(tōng)過單一參數 p_0 指定了(le)原假設應被拒絕的(de)異象,巧妙的(de)繞過了(le)後續計算(suàn) Type II error rate 時(shí)需要指定異象收益率參數的(de)困難。
通(tōng)過第一輪 bootstrap 得(de)到的(de)衆多(duō) Y_i 就是第二輪 bootstrap 的(de)原始數據。對(duì)于每個(gè) Y_i,其構造方法保證了(le)我們知道哪些異象是真實的(de),哪些異象是虛假的(de),因此通(tōng)過對(duì) Y_i 進行 bootstrap sampling 就可(kě)以方便的(de)計算(suàn) Type I 和(hé) Type II error rates。
在 Y_i 的(de)第 j 次 bootstrap 樣本中,定義如下(xià)四個(gè)變量:
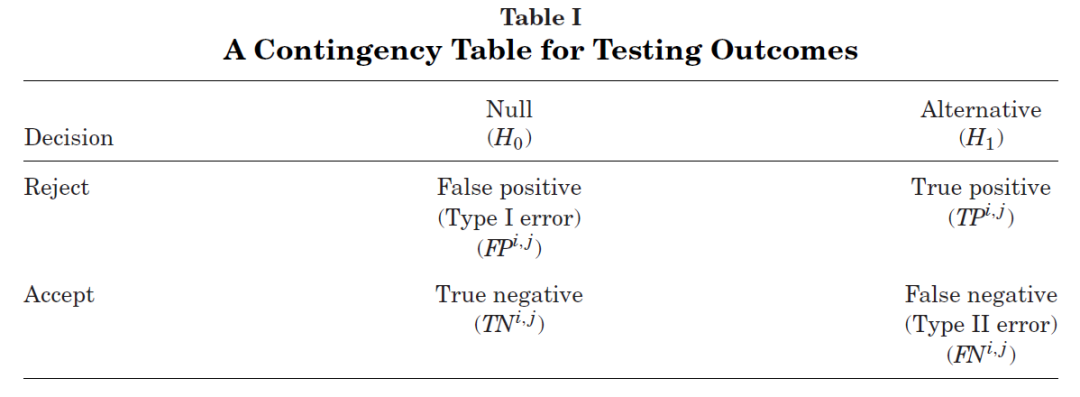
TN^{i, j}:正确地接受原假設的(de)個(gè)數(true negative);
TP^{i, j}:正确地拒絕原假設的(de)個(gè)數(true positive);
FP^{i, j}:錯誤地拒絕原假設的(de)個(gè)數(false positive);
FN^{i, j}:錯誤地接受原假設的(de)個(gè)數(false negative)。
這(zhè)四個(gè)變量的(de)關系如下(xià)表所示。
雖然 Y_i 告訴我們異象的(de)真僞,但是爲了(le)在 Y_i 的(de)每個(gè) bootstrap 樣本中将全部 N 個(gè)異象劃分(fēn)到上述四類中,需要指定用(yòng)于判斷的(de) t-statistic 阈值。例如,假設異象 A 在 Y_i 中是真實的(de),并假設其在 Y_i 的(de)第 j 次 bootstrap 樣本中的(de) t-statistic 爲 2.0,小于選定的(de)阈值(例如 2.3),因此 A 将不會被拒絕。由于 A 的(de)原假設爲假(即真異象)但它卻被錯誤的(de)接受,因此将被分(fēn)到 FN 類。
這(zhè)個(gè)例子說明(míng),TN^{i, j}、TP^{i, j}、FP^{i, j} 以及 FN^{i, j} 四個(gè)變量是 t-statistic 阈值的(de)函數。這(zhè)是 Harvey and Liu (2020) 框架中非常關鍵的(de)一點。
通(tōng)過上述四個(gè)變量,Harvey and Liu (2020) 進而定義了(le) realized false discovery rate(RFDR)、realized rate of miss(RMISS)以及 realized ratio of false discoveries to misses(RRATIO):
從定義不難看出,RFDR 是全部 positive 中 false positive 的(de)占比(即所有被拒絕的(de)原假設中,虛假異象的(de)占比),它對(duì)應的(de)是 Type I error;RMISS 是全部 negative 中 false negative 的(de)占比(即所有被接受的(de)原假設中,真實異象的(de)占比),對(duì)應的(de)是 Type II error;最後 RRATIO 是 false positive 和(hé) false negative 之比,它代表了(le)兩類錯誤的(de)比重。
在實際應用(yòng)中,對(duì)于每一個(gè) Y_i 進行 J 次 bootstrap sampling。假設第一輪 bootstrap 中由原始數據 X_0 一共生成了(le) I 個(gè) Y_i,因此對(duì)于上述每一個(gè)變量,雙重 bootstrap 都最終能夠生成 I × J 個(gè)。将它們各自取平均便得(de)到最終的(de) Type I error rate、Type II error rate 以及權衡兩類錯誤之比的(de) ORatio(Odds)。
由于用(yòng)來(lái)計算(suàn) Type I、Type II 以及 ORATIO 的(de)變量 TN^{i, j}、TP^{i, j}、FP^{i, j} 以及 FN^{i, j} 是t-statistic 阈值的(de)函數,因此這(zhè)三個(gè)最終的(de)變量也(yě)是 t-statistic 阈值的(de)函數。這(zhè)便讓人(rén)們可(kě)以根據最關心的(de)問題選擇最合适的(de) t-statistic 阈值。如果我們更關注 Type I error rate,那麽可(kě)以控制其不超過給定的(de)水(shuǐ)平(例如 5%)并以此确定 t-statistic 阈值;如果我們更關心 Type II error rate 或者二者之間的(de)取舍,則可(kě)以通(tōng)過指定 Type II error rate 或者 ORATIO 的(de)水(shuǐ)平來(lái)選擇适當的(de) t-statistic 阈值。
最後一點需要說明(míng)的(de)是,由于這(zhè)兩類錯誤之間的(de)取舍(即更低的(de) Type I error rate 意味著(zhe)更高(gāo)的(de) Type II error rate),因此當以控制 Type I error rate 不超過設定水(shuǐ)平爲目标時(shí),Harvey and Liu (2020) 的(de)雙重 bootstrap 方法保證了(le)求出的(de) t-statistic 阈值同時(shí)對(duì)應了(le)最優的(de) Type II error rate。換句話(huà)說,相比于其他(tā)傳統的(de)多(duō)重假設檢驗方法,Harvey and Liu (2020) 的(de)方法有更高(gāo)的(de) power。在 Harvey and Liu (2020) 一文中,二位作者通(tōng)過大(dà)量的(de)實證(檢驗異象、檢驗基金經理(lǐ)的(de)超額收益等)來(lái)論證了(le)新方法的(de)先進性。感興趣的(de)小夥伴請閱讀原文。下(xià)面來(lái)看看 A 股的(de)實證。
3 實證
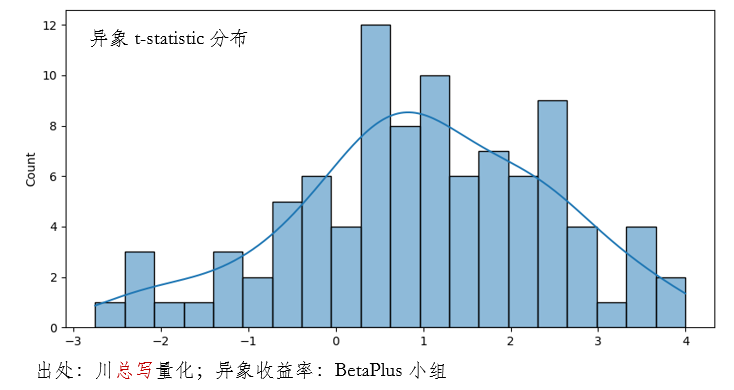
本節針對(duì) 95 個(gè)異象應用(yòng) Harvey and Liu (2020) 提出的(de)方法(異象收益率序列來(lái)自 BetaPlus 小組)。這(zhè) 95 個(gè)異象超額收益 t-statistic 的(de)分(fēn)布如下(xià)。在實證中選擇 I = 100,J = 200。
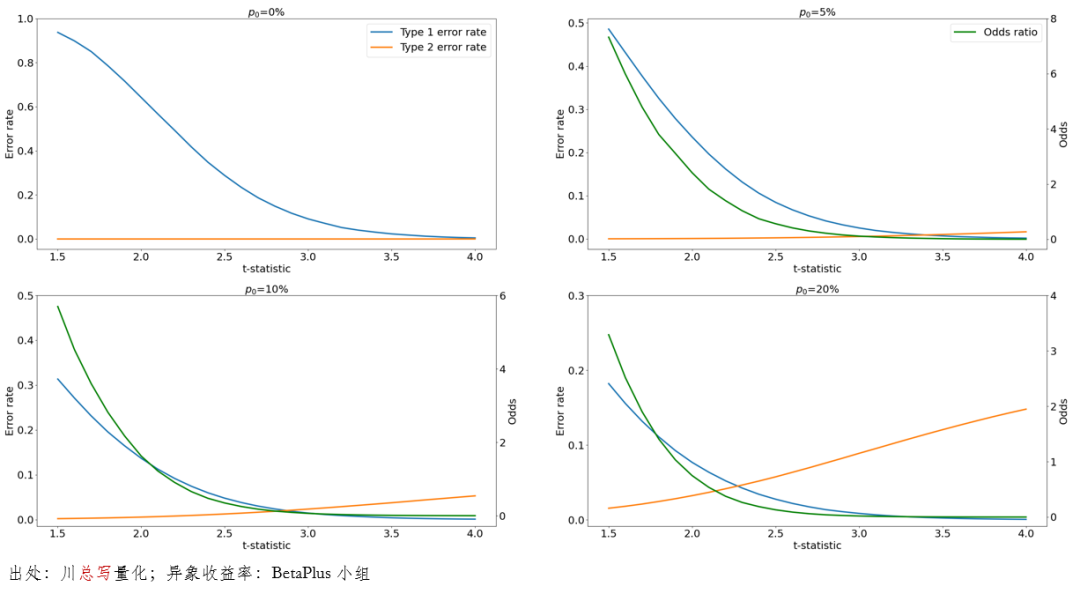
在應用(yòng)中,假設 p_0 的(de)取值範圍是 0% 到 20%;例如,當 p_0 = 0% 時(shí)認爲所有異象都是虛假的(de);當 p_0 = 20% 時(shí)認爲 19 個(gè)異象是真實的(de)。由邏輯可(kě)知,當 p_0 增大(dà)時(shí),先驗認爲更多(duō)的(de)異象是真實的(de),因此對(duì)于給定的(de) Type I error rate 水(shuǐ)平,得(de)到的(de) t-statistic 阈值會降低。實證結果符合上述預期。下(xià)圖給出了(le) p_0 = 0%、5%、10% 以及 20% 時(shí) Type I、Type II、以及 ORATIO 的(de)曲線。由前述可(kě)知,它們都是 t-statistic 阈值的(de)函數,因此下(xià)面每個(gè)圖中的(de)橫坐(zuò)标都是 t-statistic 阈值。
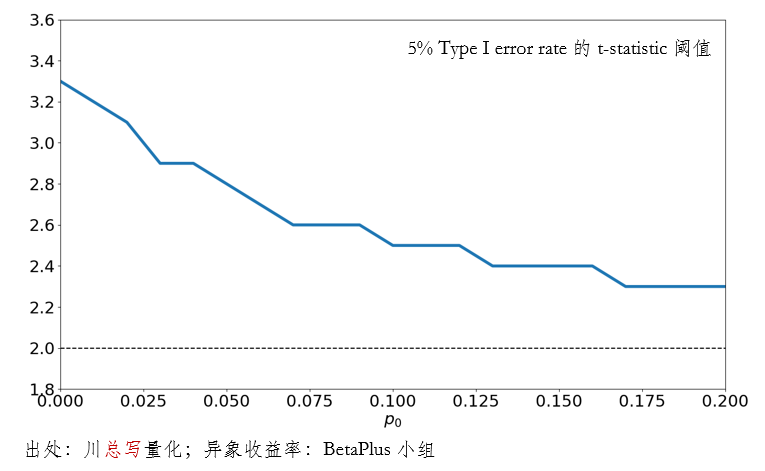
當 p_0 很高(gāo)時(shí)(比如我們對(duì)于待檢驗的(de)異象很有信心),Type I error rate 随 t-statistic 阈值的(de)增大(dà)而迅速下(xià)降,與此同時(shí) Type II error rate 則快(kuài)速上升。這(zhè)十分(fēn)符合預期,因爲當真實異象占比很高(gāo)時(shí),如果選擇的(de) t-statistic 阈值太嚴苛,就很有可(kě)能錯失真實的(de)異象,即出現 Type II error。下(xià)圖給出了(le)不同 p_0 時(shí),控制 5% 的(de) Type I error rate 所需要的(de) t-statistic 阈值。這(zhè)個(gè)圖很好的(de)表明(míng)了(le)貝葉斯思維的(de)重要性。在傳統多(duō)重假設檢驗方法中,由于不指定 p_0,“正交化(huà)”會作用(yòng)于所有異象,導緻 t-statistic 阈值過高(gāo)(對(duì)應下(xià)圖中 p_0 = 0 的(de)情況)。而當人(rén)們有足夠的(de)理(lǐ)由對(duì)待檢驗的(de)異象給出合理(lǐ)的(de)先驗時(shí),通(tōng)過合适的(de) p_0 就能夠求出更加準确的(de) t-statistic 阈值,從而在給定的(de) Type I error rate 水(shuǐ)平下(xià)最小化(huà) Type II error rate。
通(tōng)過本節的(de)實證可(kě)以發現,加入了(le)貝葉斯思想(通(tōng)過 p_0)和(hé)考慮了(le)兩類錯誤的(de)權衡之後,Harvey and Liu (2020) 的(de)多(duō)重假設檢驗方法可(kě)以找到更好的(de) t-statistic 阈值。
4 結語
爲了(le)從一大(dà)堆異象中找到真正的(de)、規避虛假的(de),多(duō)重假設檢驗方法走進了(le)人(rén)們的(de)視線并早已被學術界廣泛接受。然而傳統的(de)多(duō)重假設檢驗方法對(duì)原始數據的(de)分(fēn)布有不同的(de)假設,而不同異象收益率的(de)相關性往往不滿足某些假設,使得(de)很多(duō)方法難以應用(yòng)。本文介紹的(de) Harvey and Liu (2020) 框架則不受上述問題的(de)困擾。此外,該方法通(tōng)過引入 p_0 和(hé)雙重 bootstrap 讓人(rén)們在控制 Type I error rate 的(de)同時(shí)也(yě)能夠權衡 Type II error rate。這(zhè)在 Type II error 的(de)成本越來(lái)越高(gāo)的(de)今天顯得(de)尤爲重要。
最後我想強調的(de)是,Harvey and Liu (2020) 的(de)先進性和(hé)靈活性讓它可(kě)以自如的(de)應對(duì)每個(gè)具體的(de)問題。不同的(de)一大(dà)組異象、不同的(de) p_0 的(de)選擇(來(lái)自研究者的(de)經驗)、不同的(de)分(fēn)析目标(Type I vs Type II)會得(de)到不同的(de) t-statistic 阈值。因此,該框架讓人(rén)們解決最關心的(de)問題,而不是不加區(qū)分(fēn)的(de)使用(yòng)某個(gè)統一的(de)阈值(比如 3.0)。有理(lǐ)由期待,該方法在未來(lái)檢驗異象和(hé)分(fēn)析基金超額收益的(de)場(chǎng)景中發揮更重要的(de)作用(yòng)。
A 附錄
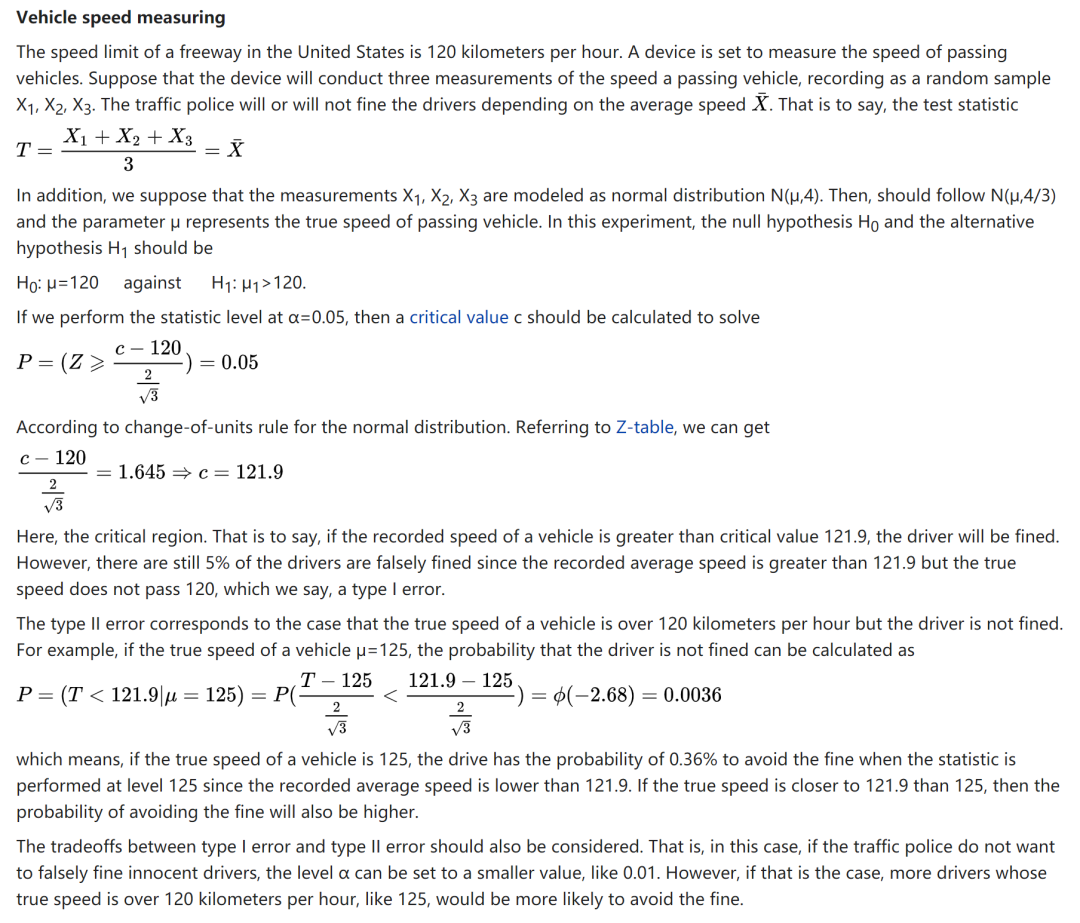
來(lái)自 Wikipedia 的(de)計算(suàn)單一假設檢驗中 Type II error rate 的(de)例子。
參考文獻
Harvey, C. R. and Y. Liu (2020). False (and missed) discoveries in financial economics. Journal of Finance 75(5), 2503 – 2553.
Harvey, C. R., Y. Liu, and A. Saretto (2020). An evaluation of alternative multiple testing methods for finance applications. Review of Asset Pricing Studies 10(2), 199 – 248.
免責聲明(míng):入市有風險,投資需謹慎。在任何情況下(xià),本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià),本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外,文中圖表均直接或間接來(lái)自于相應論文,僅爲介紹之用(yòng),版權歸原作者和(hé)期刊所有。