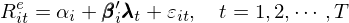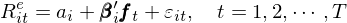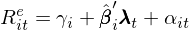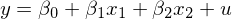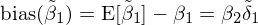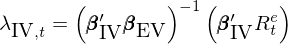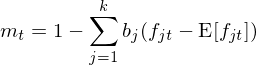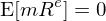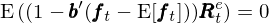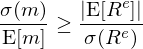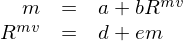實證資産定價理(lǐ)論新進展

作者：BetaPlus 小組

摘要：近年來(lái)，實證資産定價理(lǐ)論發展呈現出千帆競技、百舸争流的(de)局面。本文梳理(lǐ)其中的(de)重要成果。

1 引言

自上世紀 70 年代以來(lái)，實證資産定價研究已經走過了(le)近 50 年的(de)發展。從 CAPM 到如今家喻戶曉的(de) Fama-French 五因子、q-factor model，再到 factor zoo，線性多(duō)因子模型的(de)流行讓學界業界的(de)目光(guāng)從絕對(duì)定價模型轉變到相對(duì)定價模型。

在早期的(de)研究中，由于 Eugene Fama 開創性的(de)工作，很多(duō)研究方法被繼承了(le)下(xià)來(lái)，成爲研究實證資産定價的(de)标配。這(zhè)樣的(de)例子舉不勝舉，比如現如今所有主流的(de)多(duō)因子模型全都是通(tōng)過 portfolio sort 構造因子，然後通(tōng)過時(shí)序回歸檢驗它們的(de) pricing 能力。又比如大(dà)名鼎鼎的(de) Fama-MacBeth two-pass regression，它可(kě)以方便的(de)研究 tradable/non-tradable factors。

時(shí)至今日，雖然學界提出了(le)衆多(duō)不同的(de)多(duō)因子模型（見《主流多(duō)因子模型巡禮》），雖然它們也(yě)被拿來(lái)使用(yòng) GRS test PK 的(de)“你死我活”，然而由于它們仍然是基于傳統的(de)方法，因此不能很好的(de)回答(dá)到底哪些因子是真實的(de)、哪些因子被遺漏了(le)、因子溢價的(de)估計是否靠譜等問題。如果沒有理(lǐ)論的(de)進展，純實證的(de) factor war 似乎僅僅讓人(rén)們原地打轉。

好消息是，近幾年來(lái)學術界在實證資産定價理(lǐ)論方面還(hái)是有很多(duō)非常重要的(de)發現。這(zhè)些論文以回答(dá)最核心的(de)問題爲目标，極大(dà)的(de)推動了(le)實證資産定價的(de)發展。在本文中，BetaPlus 小組選擇了(le)其中一些最有代表性的(de)，将它們分(fēn)門别類進行介紹。希望這(zhè)樣一篇年末巨獻能幫助各位小夥伴掌握最新的(de)研究動态。

爲了(le)本文的(de)完整性，下(xià)文第二節首先簡要回顧時(shí)序回歸檢驗和(hé) Fama-MacBeth two-pass regression（具體見《股票(piào)多(duō)因子模型的(de)回歸檢驗》或《因子投資：方法與實踐》的(de)第 2.2 節）；第三節将詳細梳理(lǐ)前沿進展；第四節總結全文。

2 傳統方法

1. 時(shí)序回歸檢驗

學界主流的(de)多(duō)因子模型均是通(tōng)過時(shí)序回歸來(lái)檢驗。當因子是 tradable factors 時(shí)，首先通(tōng)過 portfolio sort 構造 factor portfolio，并估計因子溢價 λ。資産超額收益 R^e 和(hé)因子收益率滿足如下(xià)關系：

通(tōng)過 OLS 估計上述模型得(de)到每個(gè)資産對(duì)因子的(de)暴露和(hé) pricing error（α）。比如，Fama-French 三因子中的(de) HML 和(hé) SMB 都是通(tōng)過 BM 和(hé)市值（雙重）排序構造的(de)投資組合，然後用(yòng)它們的(de)收益率作爲解釋變量，通(tōng)過時(shí)序回歸來(lái)估計資産的(de)因子暴露以及資産的(de) α。

因爲人(rén)們并不知道真實的(de)因子有哪些，而這(zhè)些模型中的(de)因子都是根據某個(gè)理(lǐ)論提出來(lái)的(de)（雖然每個(gè)模型背後的(de)動機令人(rén)信服），因此它們很容易受到遺漏變量的(de)影(yǐng)響，且因子收益率的(de)計算(suàn)取決于具體如何通(tōng)過排序法構造因子的(de)投資組合（比如 Fama-French 五因子和(hé) q-factor model 中都有盈利因子，但它們選取的(de)變量以及構造方式均不同）。

2. Fama-MacBeth Regression

當因子是 non-tradable factors 時(shí)，由于無法很容易的(de)構造 factor mimicking portfolios，因此上述時(shí)序回歸檢驗無能爲力。在這(zhè)種情況下(xià)，Fama-MacBeth two-pass regression 通(tōng)常是首選。（當然，本方法也(yě)可(kě)以用(yòng)于 tradable factors。）

假設因子的(de)取值爲 f（注意是因子本身的(de)取值而非因子的(de)溢價），在兩步法中的(de)第一步先通(tōng)過求解如下(xià)時(shí)序回歸估計資産對(duì)因子的(de)暴露：

通(tōng)過 OLS 估計上述模型得(de)到 β 的(de)估計。在兩步法的(de)第二步中，在每個(gè)時(shí)刻 t 在截面上用(yòng)資産的(de)超額收益對(duì) β 回歸來(lái)估計因子溢價：

得(de)到每期因子收益率和(hé) α 之後，将它們在時(shí)序上取平均分(fēn)别得(de)到因子溢價和(hé)定價誤差的(de)估計。值得(de)一提的(de)是，Fama-MacBeth regression 是傳統截面回歸的(de)一個(gè)改進。傳統截面回歸時(shí)先将資産收益率在時(shí)序上取平均然後進行單次截面回歸，而 Fama-MacBeth regression 在每個(gè) t 時(shí)刻進行一次回歸，然後再取平均。這(zhè)麽做(zuò)的(de)好處是可(kě)以消除 α 的(de)截面相關性對(duì)回歸的(de)影(yǐng)響。

和(hé)時(shí)序回歸檢驗一樣，通(tōng)過 Fama-MacBeth regression 得(de)到的(de)多(duō)因子模型依然會受到遺漏變量的(de)影(yǐng)響 —— 所以 Barra 模型也(yě)是無法幸免的(de)，而且由于 Barra 模型中的(de)因子太多(duō)，很可(kě)能還(hái)有無關變量/weak factors 的(de)問題。另一方面，由于第一步時(shí)序回歸估計出的(de) β 存在測量誤差，因此第二步在估計因子溢價的(de)時(shí)候會出現變量誤差偏誤（errors-in-variables bias）。在這(zhè)方面，傳統的(de)解決辦法是加入 Shanken (1992) 修正。OK！以上簡要回顧了(le)傳統方法，馬上來(lái)看前沿進展。

3 前沿進展

近些年來(lái)，學術界在實證資産定價理(lǐ)論方面的(de)進展集中在因子識别（factor identification）以及因子溢價估計（factor risk premium estimate）兩方面。如前所述，如果存在模型設定偏誤問題（例如有遺漏變量或者無關變量），則因子溢價的(de)估計就會有問題，時(shí)序回歸和(hé) Fama-MacBeth 截面回歸都會受到影(yǐng)響。

大(dà)緻來(lái)說，學術界的(de)新成果可(kě)以分(fēn)爲下(xià)列五個(gè)部分(fēn)：（1）遺漏變量問題；（2）遺漏/無關變量存在時(shí)，因子溢價估計；（3）降維、聚合因子信息；（4）變量誤差問題；（5）SDF 估計。

1. 遺漏變量問題

遺漏變量問題指的(de)是模型中遺漏了(le)重要的(de)因子（解釋變量）。遺漏變量問題導緻因子溢價的(de)估計存在偏差，且更嚴重的(de)是偏差的(de)方向可(kě)正可(kě)負。

以下(xià)面這(zhè)個(gè)簡單的(de)模型爲例，假設 y 和(hé) x_1 以及 x_2 滿足如下(xià)線性回歸模型：

由于遺漏變量問題，假設令 y 對(duì) x_1 回歸，并通(tōng)過 OLS 估計。通(tōng)過簡單的(de)計量經濟學知識可(kě)知，x_1 的(de)回歸系數的(de)偏差如下(xià)：

式中 β_2 是真實模型中 y 對(duì) x_2 的(de)回歸系數，δ_1 是 x_2 對(duì) x_1 的(de)回歸系數。上式說明(míng)，β_1 的(de)偏差由 β_2 和(hé) δ_1 共同決定，它的(de)符号受這(zhè)兩部分(fēn)的(de)影(yǐng)響。遺漏變量的(de)存在使得(de)因子溢價的(de)估計是有偏的(de)（biased），它也(yě)被稱爲遺漏變量偏差（omitted variable bias）。

從傳統計量經濟學的(de)角度來(lái)說，遺漏變量問題可(kě)以通(tōng)過加入更多(duō)的(de)解釋變量來(lái)解決；此外，也(yě)可(kě)以通(tōng)過加入 fixed effect 來(lái)消除時(shí)不變的(de)遺漏變量（當然這(zhè)個(gè)假設對(duì)于資産收益率來(lái)說不一定成立）。但是在多(duō)因子模型中塞入太多(duō)的(de)因子容易造成樣本内的(de)過拟合。

當給定一個(gè)多(duō)因子模型時(shí)，如何檢驗其是否存在遺漏變量呢(ne)？爲此，Gagliardini, Ossola, and Scaillet (2019) 提出了(le)一個(gè)簡單有效的(de)方法。如果不存在遺漏變量問題，則資産對(duì)多(duō)因子模型回歸的(de)殘差中就不應該存在殘留的(de)因子結構。殘留的(de)因子結構可(kě)以通(tōng)過分(fēn)析殘差協方差矩陣最大(dà)的(de)特征值來(lái)确定。若該特征值超過了(le)一定阈值就可(kě)以認爲殘差并不獨立，存在遺漏變量問題。GOS(2019) 通(tōng)過将該方法應用(yòng)到常見的(de)多(duō)因子模型中發現，Fama and French (2015) 五因子模型和(hé) Hou, Xue, and Zhang (2015) 的(de) q-factor model 并不存在遺漏變量問題。（不知是否和(hé)使用(yòng)的(de) test assets 有關。）

除此之外，Pukthuanthong, Roll, and Subrahmanyam (2019) 以及 Feng, Giglio, and Xiu (2020) 兩篇文章(zhāng)提出了(le)如何從 factor zoo 中識别出真實因子的(de)方法，也(yě)能有效解決遺漏變量的(de)問題。先說前者，PRS(2019) 指出真實的(de)因子需要滿足兩方面的(de)特性：（1）因子必須能解釋資産的(de)共同運動，因此和(hé)資産的(de)協方差有關；（2）因子必須被定價（即因子的(de) risk premium 大(dà)于零）。基于上述特征，該文提出了(le)識别因子的(de)步驟，首先通(tōng)過上述第一點選出因子，然後通(tōng)過 Fama-MacBeth 回歸估計并檢驗選出的(de)因子的(de)溢價，并最終确定真實的(de)因子。有意思的(de)是，PRS(2019) 的(de)前半部分(fēn)需要用(yòng)到資産的(de)協方差矩陣。但是我們知道由于資産太多(duō)，因此直接計算(suàn)其協方差矩陣不切實際，正是因爲這(zhè)個(gè)原因才有了(le)使用(yòng)因子降維一說、才有了(le) Barra 模型的(de)流行。2016 年，Richard Roll 在 Q-Group 會議(yì)上報告了(le)這(zhè)篇論文。在之後的(de) Q&A 環節，台下(xià)觀衆便向他(tā)抛出了(le)資産協方差矩陣未知的(de)問題。不知道是因爲故意回避，還(hái)是因爲觀衆并非是 native speaker 因此問題說的(de)不是很清楚，最終 Roll 并沒有正面回答(dá)這(zhè)個(gè)問題。

FGX(2020) 則提出了(le)兩步 LASSO 來(lái)識别真實的(de)因子。第一步 LASSO 首先從衆多(duō)候選因子中找出能夠解釋資産預期收益率的(de)因子。但故事到這(zhè)裏還(hái)沒有結束，在第二步 LASSO 中，通(tōng)過考察“已選出因子和(hé)資産的(de)協方差”以及“剩餘因子和(hé)資産的(de)協方差”之間的(de)相關性，再選出額外的(de)因子。第二步的(de)目的(de)是爲了(le)避免第一步存在模型設定偏誤導緻遺漏變量問題。

2. 遺漏/無關變量存在時(shí)，因子溢價估計

無論是遺漏變量還(hái)是無關變量，都會對(duì)因子溢價估計造成影(yǐng)響。遺漏變量問題導緻因子溢價估計有偏，如何準确的(de)估計因子溢價以及在這(zhè)個(gè)基礎上檢驗異象的(de)超額收益就是非常重要的(de)問題。由于真實的(de)因子結構是未知的(de)，因此學術界把研究的(de)目光(guāng)移到了(le)隐性因子模型上。在隐性因子模型框架下(xià)，任何一個(gè)可(kě)觀測因子的(de)風險溢價等于它對(duì)隐性因子的(de)暴露乘以隐性因子的(de)溢價。

在這(zhè)個(gè)性質下(xià)，Giglio and Xiu (2020) 利用(yòng) PCA，通(tōng)過隐性因子模型估計可(kě)觀測因子的(de)溢價。計量經濟學中的(de)重要性質使得(de) PCA 在這(zhè)方面大(dà)有可(kě)爲。首先，利用(yòng)線性因子模型的(de)旋轉不變性，即便隻能觀察到隐性因子的(de)某個(gè)滿秩變換，也(yě)不妨礙估計可(kě)觀測因子的(de)溢價。其次，隻要隐性因子足夠強，PCA 總是可(kě)以複原對(duì)因子空間的(de)某個(gè)旋轉變換。通(tōng)過這(zhè)兩個(gè)性質，GX(2020) 準确的(de)估計了(le)可(kě)觀測因子的(de)溢價（更多(duō)介紹見《因子投資：方法與實踐》的(de) 6.8.4 節）。

再來(lái)看後者。由計量經濟學的(de)知識可(kě)知，如果在回歸模型中存在無關變量（irrelevant variables），雖然不會影(yǐng)響其他(tā)解釋變量回歸系數的(de)無偏性，但是會增大(dà)回歸系數的(de) standard error（降低顯著性），使得(de)估計量 less efficient。

在多(duō)因子模型的(de)場(chǎng)景下(xià)，上述過度識别問題的(de)表現爲模型中加入了(le) weak factors，即和(hé)資産相關性非常微弱的(de)因子。在這(zhè)樣的(de)設定下(xià)，Gospodinov, Kan, and Robotti (2014) 發現很容易出現的(de)結果是 weak factors 的(de)因子溢價很顯著，而真實的(de)因子的(de)溢價不顯著，從而造成真實的(de)因子被舍棄。在這(zhè)方面，不得(de)不說的(de)兩篇文章(zhāng)是 Bryzgalova (2016) 和(hé) Bryzgalova, Huang, and Julliard (2019)。這(zhè)兩篇文章(zhāng)雖然尚未發出來(lái)，但目前分(fēn)别在 RFS 和(hé) JF 的(de) R&R 階段。從這(zhè)兩篇文章(zhāng)的(de)貢獻來(lái)看，被頂刊接收應該隻是時(shí)間問題。這(zhè)兩篇文章(zhāng)給出了(le)存在 weak factors 的(de)情況下(xià)如何準确估計其他(tā)因子的(de)溢價。

除此之外，再插一嘴 GX(2020)。雖然該文的(de)标題爲 omitted factors，但它實際上隐含地考慮了(le) weak factors 問題，因爲該方法不僅僅适用(yòng)于 tradable factors，也(yě)适用(yòng)于 non-tradable factors，而後者是 weak factors 的(de)重災區(qū)（對(duì) tradable factors 來(lái)說，幾乎不存在這(zhè)個(gè)問題）。另外，Kleibergen and Zhan (2018, 2020) 則直接給出了(le)估計 non-tradable factors 因子溢價的(de)方法。對(duì)于這(zhè)類因子，Fama-MacBeth 回歸的(de)第一步時(shí)序回歸往往無法得(de)到靠譜的(de) β，因此這(zhè)些新方法就變得(de)十分(fēn)必要。

在結束這(zhè)部分(fēn)的(de)討(tǎo)論之前，另一篇需要介紹的(de)文章(zhāng)是 Giglio, Liao, and Xiu (2020)。與 GX(2020) 不同，GLX(2020) 的(de)主要目标是研究基金的(de)超額收益是否顯著（區(qū)分(fēn)運氣和(hé)能力）。由于超額收益是相對(duì)定價模型而言的(de)，因此該問題顯然涉及到因子溢價估計問題。簡答(dá)來(lái)說，GLX(2020) 分(fēn)爲四步：（1）通(tōng)過時(shí)序回歸确定基金對(duì)一組給定因子的(de)暴露；（2）對(duì)殘差利用(yòng) GX(2020) 中的(de) PCA 識别出遺漏的(de)因子，并獲得(de)基金在這(zhè)些因子上的(de)暴露；（3）通(tōng)過截面回歸估計所有因子的(de)溢價以及基金的(de)超額收益；（4）通(tōng)過多(duō)重假設檢驗算(suàn)法修正 t-statistics 并判斷哪些基金能夠獲得(de)超額收益。（關于 GLX2020 的(de)解讀請點擊此處。）

3. 聚合因子信息

由于 factor zoo 造成的(de)維數災難，把它們都放在多(duō)因子模型中顯然是不切實際的(de)。因此，第三類研究正是如何以更好的(de)解釋資産預期收益的(de)截面差異爲目标，通(tōng)過降維将衆多(duō)因子的(de)信息聚合在一起。在這(zhè)方面，近兩年金融學、計量經濟學乃至統計學頂刊上也(yě)發表了(le)多(duō)篇重磅文章(zhāng)。

與 GX(2020) 類似，Kelly, Pruitt, and Su (2019) 同樣将真實因子視作不可(kě)觀測的(de)隐性因子并通(tōng)過 PCA 來(lái)提取信息。該文采用(yòng) Kelly, Pruitt, and Su (2017) 的(de)工具變量 IPCA 方法，引入大(dà)量公司特征作爲因子暴露和(hé)超額收益的(de)工具變量，構建了(le) IPCA 因子。實證結果顯示，IPCA 方法的(de)确具有較好的(de)表現。此外，Kelly, Moskowitz, and Pruitt (2020) 也(yě)采用(yòng) IPCA 方法來(lái)解釋 momentum。前述幾篇文章(zhāng)基本都來(lái)自對(duì) Fan, Liao, and Wang (2016) 提出的(de) projected PCA 方法的(de)應用(yòng)和(hé)拓展。對(duì)背後統計理(lǐ)論感興趣的(de)小夥伴建議(yì)去看範劍青老師的(de)原文。

另外兩篇文章(zhāng)是 Lettau and Pelger (2020a, b)，其中一篇發在計量經濟學頂刊上介紹方法，另一篇則發在金融學頂刊上主要講應用(yòng)。他(tā)們認爲上述利用(yòng) PCA 的(de)研究雖然新穎，但是僅僅利用(yòng)了(le)收益率的(de)二階矩信息，丢失掉了(le)原始因子和(hé)資産收益率在截面上的(de)關系，即一階矩信息。爲此，該方法在經典 PCA 問題中加入了(le)代表一階矩的(de)額外項，提出了(le) risk premium PCA（PR-PCA）方法。關于 IPCA 和(hé) RP-PCA 的(de)更詳細介紹請點擊這(zhè)裏。

實證分(fēn)析表明(míng)，RP-PCA 在絕大(dà)多(duō)數情況下(xià)都優于傳統 PCA，且統計檢驗表明(míng)，通(tōng)過使用(yòng)五個(gè) PR-PCA 因子能夠很好地反映股票(piào)的(de)系統性風險，且同時(shí)能夠解釋它們收益率的(de)截面差異。對(duì)因子構成進行進一步探索發現，這(zhè)五個(gè)因子都有很好的(de)經濟學基礎。

4. 變量誤差問題

變量誤差（errors-in-variables）問題主要影(yǐng)響 Fama-MacBeth 截面回歸。在 Fama-MacBeth 回歸的(de)第一步，即通(tōng)過時(shí)序回歸估計因子暴露 β。在第二步，上述 β 被用(yòng)來(lái)當作解釋變量，估計因子溢價。EIV 問題使得(de)該因子溢價的(de)估計存在偏差（biased toward zero，被稱爲 attenuation bias）。除此之外，某變量的(de) EIV 問題同樣會導緻其他(tā)因子（哪怕這(zhè)些因子的(de) β 不存在 EIV 問題）的(de)因子溢價估計出現偏差（contamination bias）。

鑒于 EIV 問題，Fama and MacBeth (1973) 在檢驗 CAPM 的(de)時(shí)候采用(yòng) portfolios 而非個(gè)股作爲 test assets。這(zhè)種做(zuò)法也(yě)被保留了(le)下(xià)來(lái)。在如今檢驗多(duō)因子模型時(shí)或估計因子溢價時(shí)，常用(yòng) portfolios 作爲 test assets。然而，将個(gè)股分(fēn)組會丢掉很多(duō)個(gè)股截面上的(de)特征。如果待檢驗的(de)因子和(hé)這(zhè)些 portfolios 的(de)分(fēn)組屬性正交，用(yòng)它們作爲 test assets 就無法發現這(zhè)些因子的(de)溢價。因此，比起使用(yòng)各種 firm characteristics 單變量或雙重排序構造的(de) portfolios，個(gè)股仍然是更好的(de) test assets。

爲了(le)解決個(gè)股作爲 test assets 時(shí)的(de) EIV 問題，Jegadeesh et al. (2019) 提出了(le)工具變量估計量（IV estimator），前文《Which beta ?》對(duì)此進行了(le)詳盡的(de)討(tǎo)論。該 IV estimator 爲：

式中 β_IV 和(hé) β_EV 分(fēn)别爲 instrumental 和(hé) explanatory variables：β_EV 是對(duì)傳統時(shí)序回歸得(de)到的(de) β 的(de)估計，β_IV 是 β_EV 的(de)工具變量。Jegadeesh et al. (2019) 使用(yòng)互不重疊的(de)曆史數據分(fēn)别進行時(shí)序回歸求解 β_IV 和(hé) β_EV，并指出正因如此，它們在截面上是不相關的(de)，可(kě)以規避 EIV 問題。通(tōng)過模拟數據，他(tā)們證實了(le)采用(yòng) IV estimator 後，無論事前還(hái)是事後，因子溢價的(de)估計都是無偏的(de)。此外，Pukthuanthong et al. (2020) 在該文的(de)基礎上，研究了(le)如何估計 non-tradable factors 的(de)溢價。

談到更好的(de)因子暴露，不得(de)不提的(de)另一種做(zuò)法就是業界（例如 Barra）直接使用(yòng) firm characteristics 作爲因子暴露。實證結果顯示 firm characteristics 比起個(gè)股收益率對(duì)因子收益率的(de)時(shí)序回歸系數更能預測個(gè)股未來(lái)收益率（例如 Lewellen 2015）。此外，Jegadeesh et al. (2019) 的(de)實證結果發現，當控制 firm characteristics 後，使用(yòng) IV estimator 也(yě)無法獲得(de)顯著因子溢價。與此同時(shí)，Fama and French (2020) 比較了(le)兩類 β 構造的(de)多(duō)因子模型，發現用(yòng) firm characteristics 做(zuò)暴露的(de)模型更好（見《Which beta (II)?》、《A new norm ?》）。

盡管 firm characteristics 表現出了(le)比時(shí)序回歸 β 更好的(de)預測性，但人(rén)們仍然不禁要發問它們難道就完全對(duì) EIV 問題免疫嗎？答(dá)案是否定的(de)。比如，時(shí)變的(de) firm characteristics 受到過去收益率的(de)影(yǐng)響（例如市值、BM、EP），firm characteristics 和(hé)測量誤差之間存在截面相關性。因此，即便是 firm characteristics 作爲 β，因子溢價的(de)估計也(yě)受到 EIV 的(de)影(yǐng)響。

面對(duì)上述困境，定量修正 β 的(de)測量誤差無疑更有價值。無論是用(yòng)時(shí)序回歸系數還(hái)是公司特征作爲 β，都會因此而改善 EIV 問題。這(zhè)方面的(de)代表性成果是 Chordia, Goyal, and Shanken (2019)。該文提出了(le)定量修正因子暴露 EIV 問題的(de)方法。該方法能很大(dà)程度上消除傳統 Fama-MacBeth 兩步法中的(de) EIV 問題。不過盡管如此他(tā)們也(yě)發現，和(hé)時(shí)序回歸系數相比，firm characteristics 更能夠解釋股票(piào)預期收益率的(de)截面差異。

5. 估計 SDF

新進展的(de)最後一個(gè)方向是估計随機折現因子（Stochastic Discount Factor，即 SDF）。SDF 可(kě)以寫成因子的(de)線性組合：

其中 m_t 爲 SDF，f_{jt} 爲因子 j 在 t 期的(de)取值（對(duì)于 tradable factors，它就是因子收益率；對(duì)于 non-tradable factors，它就是因子本身的(de)取值）。此外，由無套利定價公式可(kě)知：

将 SDF 的(de)定義套入上式并可(kě)以通(tōng)過 GMM（Hansen 1982，見《Generalized method of moments》）來(lái)估計參數 b：

由上式可(kě)知，估計 SDF 就轉化(huà)爲求解參數 b 的(de)問題，且通(tōng)過 GMM 來(lái)估計 b 等價于使用(yòng)資産的(de)超額收益 E[R^e] 對(duì)資産和(hé)因子的(de)協方差 cov(R^e, f) 回歸（Cochrane 2005）。由資産定價原理(lǐ)可(kě)知，SDF 和(hé)資産的(de)超額收益滿足如下(xià)關系：

這(zhè)個(gè)看似簡單的(de)關系有很多(duō)非常重要的(de) implications。其中之一是隻有在 mean-variance frontier 上的(de)資産，上述關系中的(de)等式才成立，且所有 mean-variance frontier 上的(de)資産都和(hé) SDF 完全（負）相關，因此所有這(zhè)些資産本身也(yě)都是完全（正）相關。這(zhè)種相關性完美(měi)的(de)将 SDF 和(hé) mean-variance frontier 上任意資産的(de)收益率聯系在一起：

這(zhè)兩個(gè)等價關系說明(míng)隻要找到 mean-variance frontier 上的(de)任意資産，就相當于找到了(le) SDF，就找到了(le)給其他(tā)任何資産定價所需要的(de)信息。用(yòng) Cochrane 的(de)話(huà)說就是“any mean variance efficient return carries all pricing information”。而上述性質對(duì)估計 SDF 的(de)借鑒意義是什(shén)麽呢(ne)？由數學上的(de)性質可(kě)知，mean-variance frontier 上的(de)資産有最大(dà)的(de) Sharpe Ratio，因此隻要能夠想辦法用(yòng)所有 tradable assets，例如個(gè)股或者各種 factor portfolios，來(lái)構造 SR 最高(gāo)的(de) tangency portfolio，就可(kě)以用(yòng)它來(lái)估計 SDF 了(le)。

通(tōng)過線性代數運算(suàn)可(kě)知，當使用(yòng)一組 assets 同時(shí)作爲構造 SDF 的(de)因子以及檢驗矩條件的(de)資産時(shí)，SDF 參數 b 的(de)求解等價于通(tōng)過這(zhè)組 assets 求解 mean-variance optimization 的(de)最優權重。因此，一切就連起來(lái)了(le)，我們隻需要在衆多(duō) tradable assets 中以最大(dà)化(huà) SR 爲目标找出合适的(de)并構造 tangency portfolio 即可(kě)，tangency portfolio 的(de)權重就是 SDF 的(de)參數 b。

在求解 tangency portfolio 時(shí)，有兩個(gè)難點需要考慮：（1）選擇哪些 assets；（2）如何以獲得(de)樣本外最高(gāo) SR 爲目标來(lái)求解 MVO 問題。在這(zhè)方面，Kozak, Nagel, and Santosh (2020) 和(hé) Bryzgalova, Pelger, and Zhu (2020) 分(fēn)别給出了(le)答(dá)案。在 assets 方面，KNS(2020) 可(kě)以大(dà)緻理(lǐ)解爲從大(dà)量因子中提取信息來(lái)估計 SDF。在最優化(huà)方面，由于因子太多(duō)導緻的(de)過拟合和(hé)維數災難問題，因此該文使用(yòng)了(le) elastic net 方法，同時(shí)考慮了(le) ridge regression 和(hé) LASSO 對(duì) variance 進行了(le) shrinkage。實證研究發現，隻有當 SDF 聚合了(le)大(dà)量因子的(de)信息之後，它才能比較好的(de)給其他(tā)資産定價。這(zhè)個(gè)結果傳遞出來(lái)的(de)含義是能夠影(yǐng)響資産預期收益的(de)因子可(kě)能有很多(duō)。

Bryzgalova, Pelger, and Zhu (2020) 可(kě)以認爲是 KNS(2020) 的(de)擴展。首先在 assets 方面，BPZ(2020) 以給定的(de) firm characteristics 爲劃分(fēn)依據，通(tōng)過構建 asset pricing tree 構成了(le)大(dà)量的(de) portfolios，然後從中挑選出最能代表股票(piào)收益率截面差異的(de) portfolios 作爲 basis assets。在最優化(huà)方面，KNS(2020) 隻考慮了(le)對(duì) variance 的(de) shrinkage，而 BPZ(2020) 額外加入了(le)對(duì) mean 的(de) shrinkage。整體來(lái)看，BPZ(2020) 較 KNS(2020) 使用(yòng)了(le)更優的(de) assets 以及更穩健的(de) MVO，所以取得(de)了(le)更好的(de)效果。

此外，值得(de)一提的(de)是 BPZ(2020) 的(de) basis portfolios 也(yě)可(kě)以用(yòng)來(lái)取代傳統的(de) portfolio sort 組合，以作爲 test assets 來(lái)檢驗多(duō)因子模型或者估計因子溢價。對(duì)于這(zhè)兩種場(chǎng)景，test assets 無疑非常重要。當 test assets 不合理(lǐ)的(de)時(shí)候，使用(yòng) GRS test 一通(tōng)分(fēn)析，也(yě)僅是能從候選模型中選出能夠解釋那些 test assets 的(de)，但它這(zhè)模型本身也(yě)未必就怎麽樣（GRS test 結果和(hé)所選用(yòng)的(de) test assets 密切相關）。

由于個(gè)股的(de) EIV 問題，傳統做(zuò)法是使用(yòng)各種變量排序構造的(de)投資組合來(lái)做(zuò) test assets，但如今我們都知道這(zhè)麽做(zuò)有很大(dà)的(de)問題（Lewellen, Nagel, and Shanken 2010），比如很難考慮變量和(hé)收益率的(de)非線性關系，以及這(zhè)類 test assets 存在很強的(de) factor structure。而使用(yòng) BPZ(2020) 的(de) basis assets 作爲 test assets 則不存在這(zhè)些問題。前不久，BPZ(2020) 獲得(de)了(le) 2020 年 SFS 北(běi)美(měi)年會資産定價方面的(de)最佳論文獎。鑒于 RFS 是 SFS 旗下(xià)的(de)期刊，估計 BPZ(2020) 也(yě)早晚會出現在頂刊上，而通(tōng)過該文方法構造的(de)全新 test assets 勢必會深遠(yuǎn)影(yǐng)響今後多(duō)因子模型檢驗和(hé)因子溢價估計方面的(de)研究。

4 結語

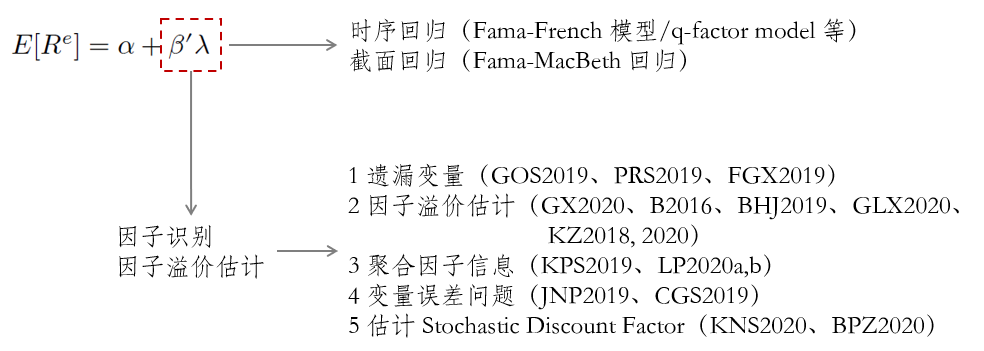
呼！終于寫完了(le)。下(xià)面是“一圖勝千言”環節。下(xià)圖總結了(le)本文所梳理(lǐ)的(de)内容。由于所學和(hé)精力有限，肯定還(hái)有好多(duō)重要貢獻被遺漏了(le)，所以也(yě)鼓勵公衆号的(de)小夥伴們自己找起來(lái)、讀起來(lái)。

近年來(lái)，在頂刊上發表實證資産定價的(de)文章(zhāng)中，一個(gè)明(míng)顯的(de)趨勢是純實證的(de)越來(lái)越少（比如挖掘個(gè) anomaly 之類的(de)），能發出來(lái)的(de)也(yě)大(dà)多(duō)使用(yòng)了(le)獨門的(de)數據以及在收集數據時(shí)進行了(le)重體力勞動，比如 Linnainmaa and Roberts (2018)，而本文介紹的(de)這(zhè)類推動理(lǐ)論進展的(de)文章(zhāng)則呈現百家争鳴的(de)局面。毫無疑問，後者才更有生命力，它們爲解決實證資産定價裏面的(de)各種 big problems 做(zuò)出了(le)卓越貢獻。

展望 2021，我們也(yě)希望能從上述重磅文獻中精挑一些最經典的(de)，爲各位帶來(lái)更加系統和(hé)詳盡的(de)解讀。正如今年五月(yuè) Review of Financial Studies 發行的(de)特刊 New methods in the cross-section 帶給人(rén)的(de)驚喜一樣，本文所涉及的(de)以及沒有涉及的(de)諸多(duō)新成果，都讓我們對(duì)實證資産定價的(de)未來(lái)足夠期待！

參考文獻

Bryzgalova, S. (2016). Spurious factors in linear asset pricing models. Working paper.

Bryzgalova, S., J. Huang, and C. Julliard (2019). Bayesian solutions for the factor zoo: We just ran two quadrillion models. Working paper.

Bryzgalova, S., M. Pelger, and J. Zhu (2020). Forest through the trees: Building cross-sections of stock returns. Working paper.

Chordia, T., A. Goyal, and J. A. Shanken (2019). Cross-sectional asset pricing with individual stocks: Betas versus characteristics. Working paper.

Cochrane, J. H. (2005). Asset Pricing (Revised Edition). Princeton, NJ: Princeton University Press.

Fama, E. F. and K. R. French (2015). A five-factor asset pricing model. Journal of Financial Economics 116(1), 1 – 22.

Fama, E. F. and K. R. French (2020). Comparing cross-section and time-series factor models. Review of Financial Studies 33(5), 1891 – 1926.

Fama, E. F. and J. D. MacBeth (1973). Risk, return, and equilibrium: Empirical tests. Journal of Political Economy 81(3), 607–636.

Fan, J., Y. Liao, and W. Wang (2016). Projected principal component analysis in factor models. Annals of Statistics 44(1), 219 – 254.

Feng, G., S. Giglio, and D. Xiu (2020). Taming the factor zoo: A test of new factors. Journal of Finance 75(3), 1327 – 1370.

Gagliardini, P., E. Ossola, and O. Scaillet (2019). A diagnostic criterion for approximate factor structure. Journal of Econometrics 212(2), 503 – 521.

Giglio, S., Y. Liao, and D. Xiu (2020). Thousands of alpha tests. Review of Financial Studies forthcoming.

Giglio, S. and D. Xiu (2020). Asset pricing with omitted factors. Journal of Political Economy forthcoming.

Gospodinov, N., R. Kan, and C. Robotti (2014). Misspecification-robust inference in linear asset-pricing models with irrelevant risk factors. Review of Financial Studies 27(7), 2139 – 2170.

Hansen, L. P. (1982). Large sample properties of generalized method of moments estimators. Econometrica 50(4), 1029 – 1054.

Hou, K., C. Xue, and L. Zhang (2015). Digesting anomalies: An investment approach. Review of Financial Studies 28(3), 650 – 705.

Jegadeesh, N., J. Noh, K. Pukthuanthong, R. Roll, and J. Wang (2019). Empirical tests of asset pricing models with individual assets: Resolving the errors-in-variables bias in risk premium estimation. Journal of Financial Economics 133(2), 273 – 298.

Kelly, B. T., T. J. Moskowitz, and S. Pruitt (2020). Understanding momentum and reversals. Journal of Financial Economics forthcoming.

Kelly, B. T., S. Pruitt, and Y. Su (2017). Instrumented principal component analysis. Working paper.

Kelly, B. T., S. Pruitt, and Y. Su (2019). Characteristics are covariances: A unified model of risk and return. Journal of Financial Economics 134(3), 501 – 524.

Kleibergen, F. and Z. Zhan (2018). Identification-robust inference on risk premia of mimicking portfolios of non-traded factors. Journal of Financial Econometrics 16(2), 155 – 190.

Kleibergen, F. and Z. Zhan (2020). Robust inference for consumption-based asset pricing. Journal of Finance 75(1), 507 – 550.

Kozak, S., S. Nagel, and S. Santosh (2020). Shrinking the cross-section. Journal of Financial Economics 135(2), 271 – 292.

Lettau, M. and M. Pelger (2020a). Factors that fit the time series and cross-section of stocks returns. Review of Financial Studies 33(5), 2274 – 2325.

Lettau, M. and M. Pelger (2020b). Estimating latent asset-pricing factors. Journal of Econometrics 218(1), 1 – 31.

Lewellen, J. (2015). The cross-section of expected stock returns. Critical Finance Review 4, 1 – 44.

Lewellen, J., S. Nagel, and J. Shanken (2010). A skeptical appraisal of asset pricing tests. Journal of Financial Economics 96(2), 175 – 194.

Linnainmaa, J. T. and M. R. Roberts (2018). The history of the cross-section of stock returns. Review of Financial Studies 31(7), 2606 – 2649.

Pukthuanthong, K., R. Roll, and A. Subrahmanyam (2019). A protocol for factor identification. Review of Financial Studies 32(4), 1573 – 1607.

Pukthuanthong, K., R. Roll, J. Wang, and T. Zhang (2020). A tool kit for factor-mimicking portfolios. Working paper.

Shanken, J. (1992). On the estimation of beta-pricing models. Review of Financial Studies 5(1), 1 – 33.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。