分(fēn)形市場(chǎng)假說

作者：石川

摘要：分(fēn)形市場(chǎng)假說可(kě)以解釋有效市場(chǎng)假說無法解釋的(de)市場(chǎng)現象。分(fēn)形時(shí)間序列可(kě)以更加合理(lǐ)的(de)對(duì)收益率或者價格序列建模。

0 引言：英國的(de)海岸線有多(duō)長(cháng)

問：“要想确定英國的(de)海岸線有多(duō)長(cháng)得(de)分(fēn)幾步？”

答(dá)：“三步！第一步，确定度量的(de)比例；第二步，按選擇的(de)比例沿海岸線度量；第三步，計算(suàn)并記錄結果。”

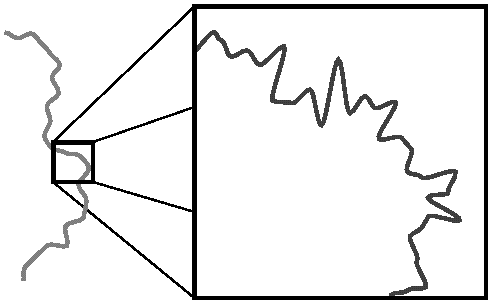
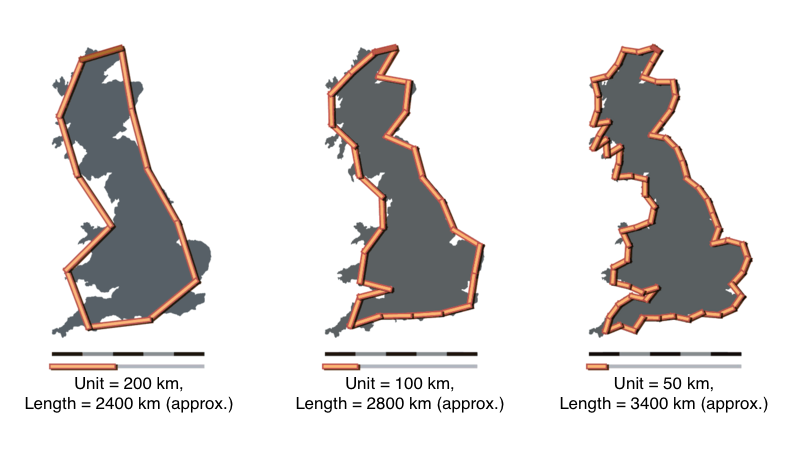
然而，輕松之餘，這(zhè)實際上是個(gè)非常嚴謹的(de)數學問題，但它又是個(gè)哲學問題。因爲無論你的(de)度量尺度選的(de)多(duō)小，在比該尺度更小的(de)尺度上，海岸線仍然會呈現出大(dà)量的(de)無規則性（如下(xià)圖），所以選擇不同的(de)尺度會得(de)到不同的(de)測量結果。

比如，如果我們的(de)測量尺度是 200 公裏，那麽得(de)出的(de)結果大(dà)概是 2400 公裏；當測量尺度變爲 100 公裏時(shí)，得(de)到的(de)結果是 2800 公裏；如果進一步縮小測量尺度到 50 公裏，得(de)到的(de)距離是 3400 公裏。可(kě)見，随著(zhe)度量尺度越來(lái)越精細，測量得(de)到的(de)英國海岸線的(de)長(cháng)度是一直增加的(de)！

英國的(de)海岸線隻是真實世界中不規則的(de)、支離破碎的(de)幾何形态的(de)一個(gè)普通(tōng)的(de)例子。類似的(de)例子還(hái)包括山峰的(de)輪廓、股票(piào)的(de) K 線等。對(duì)于這(zhè)些雜(zá)亂無章(zhāng)的(de)幾何形态和(hé)自然現象，經典幾何無能爲力，而“分(fēn)形”的(de)概念卻大(dà)有作爲（Mandelbrot 1977, 1982）。

1 分(fēn)形

分(fēn)形的(de)概念由 Mandelbrot 提出。通(tōng)俗的(de)說，分(fēn)形是局部和(hé)整體有某種方式相似的(de)形狀。該定義強調局部和(hé)整體的(de)自相似性。用(yòng)上面英國海岸線的(de)例子來(lái)說，如果我們用(yòng)一個(gè)可(kě)變焦的(de)放大(dà)鏡來(lái)研究它的(de)不同局部，那麽無論我們選擇什(shén)麽樣的(de)焦距，我們看到的(de)無規則幾何形狀都是類似的(de)。又或者以股票(piào)的(de)K線爲例，不管我們看 5 分(fēn)鐘(zhōng) K 線，15 分(fēn)鐘(zhōng) K 線，日 K 線還(hái)是周 K 線（即我們在不同的(de)頻(pín)率上觀察），我們看到的(de) K 線的(de)随機形态也(yě)具有統計意義上的(de)自相似性。

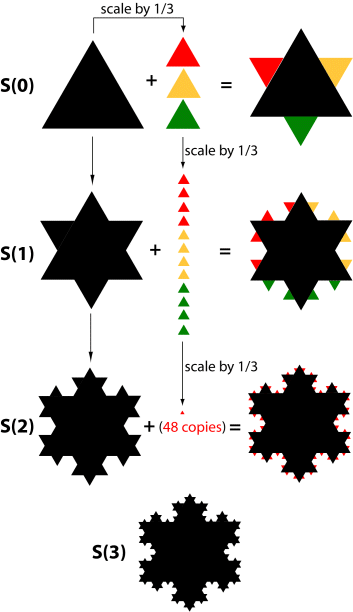
一個(gè)經典的(de)分(fēn)形例子如下(xià)面的(de) Koch 曲線（又稱 Koch 雪(xuě)花）。它由一個(gè)等邊三角形按一定的(de)規則無限遞歸構成，每一步都在上一步的(de)基礎上構造出形狀相似但尺度更小（上一步中三角形的(de) 1/3）的(de)等邊三角形。Koch 曲線的(de)長(cháng)度是無窮大(dà)的(de)。但是無論我們以哪個(gè)尺度觀察，看到的(de)都是等邊三角形。這(zhè)就是局部和(hé)整體自相似性的(de)完美(měi)體現。

迄今爲止，分(fēn)形并沒有嚴格的(de)定義（雖然它在數學上有嚴格和(hé)精密的(de)表達式），但分(fēn)形具有以下(xià)特征：

2 分(fēn)形市場(chǎng)假說

Peters 将分(fēn)形的(de)概念引入到經濟系統中，提出了(le)分(fēn)形市場(chǎng)假說 Fractal Market Hypothesis（Peters 1994）。該理(lǐ)論被認爲比有效市場(chǎng)假說更能解釋資本市場(chǎng)的(de)動态變化(huà)。分(fēn)形市場(chǎng)假說爲金融市場(chǎng)的(de)研究搭建了(le)全新的(de)框架。它認爲：

由于市場(chǎng)由數目衆多(duō)的(de)具有不同投資期限的(de)投資者構成，因此市場(chǎng)呈現分(fēn)形結構。在一個(gè)呈現分(fēn)形特點的(de)穩定的(de)市場(chǎng)中，不同期限的(de)投資者往往關注不同的(de)信息，他(tā)們會按照(zhào)各自的(de)投資期限做(zuò)有利自己的(de)投資操作。比如當短期投機者因爲熱(rè)點減少而賣出股票(piào)時(shí)，長(cháng)期的(de)價值投資者便可(kě)能會在價格下(xià)降到他(tā)認爲的(de)合理(lǐ)位置買入。這(zhè)就保證了(le)市場(chǎng)的(de)流動性。當市場(chǎng)的(de)分(fēn)形結構沒有變化(huà)時(shí)，市場(chǎng)就是穩定的(de)。

但是，一旦市場(chǎng)中的(de)所有投資者的(de)投資期限都統一時(shí)，市場(chǎng)就會因爲缺乏流動性而崩潰。比如在金融危機時(shí)，金融市場(chǎng)未來(lái)的(de)不确定性使所有投資者都望而卻步。因此，所有投資者都想立刻賣出自己手中的(de)籌碼，這(zhè)就造成了(le)流動性的(de)驟然枯竭。當風暴過去、市場(chǎng)開始緩慢(màn)恢複時(shí)，投資者們逐步對(duì)市場(chǎng)産生新的(de)理(lǐ)性認知，從而市場(chǎng)中再一次充滿了(le)不同投資期限的(de)投資者，這(zhè)時(shí)便産生了(le)一個(gè)新的(de)具有分(fēn)形特征的(de)穩定市場(chǎng)。

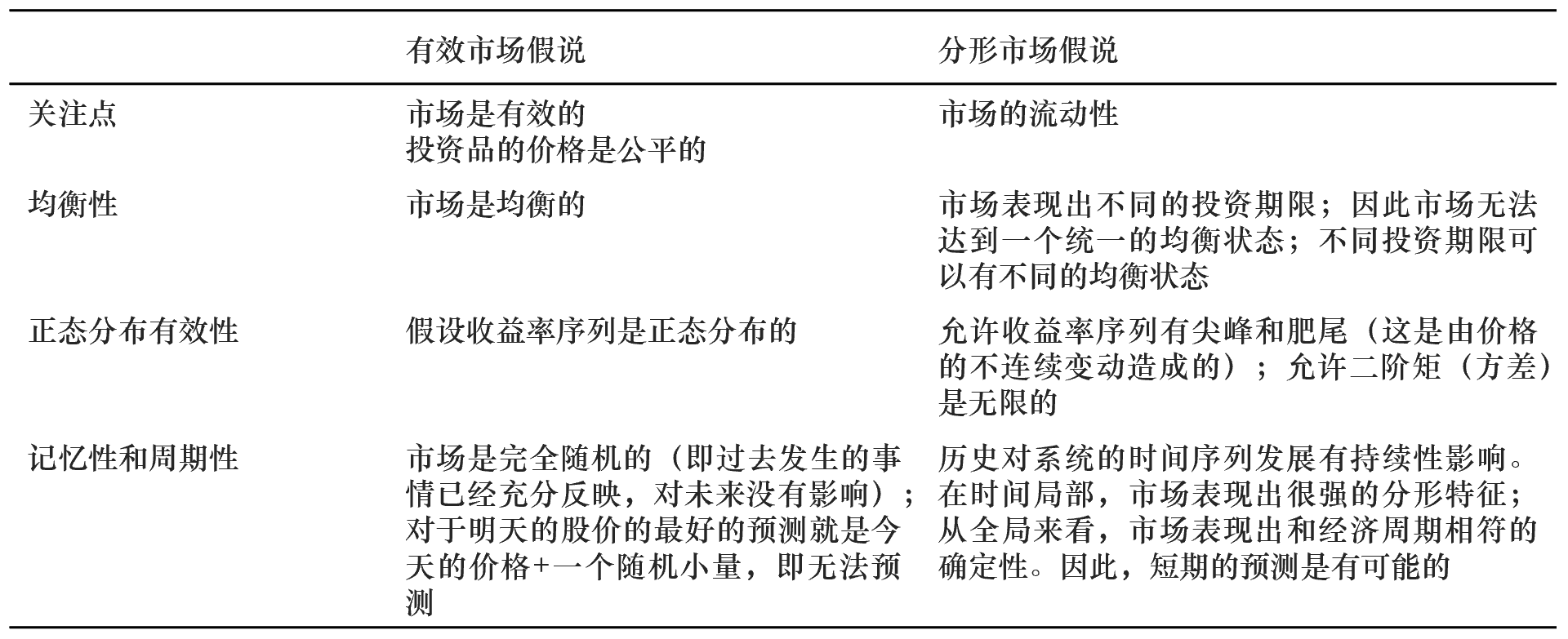
分(fēn)形市場(chǎng)假說和(hé)有效市場(chǎng)假說的(de)主要區(qū)别如下(xià)表所示。

3 分(fēn)形時(shí)間序列

具有分(fēn)形特性的(de)收益率序列就是分(fēn)形時(shí)間序列。分(fēn)形時(shí)間序列一般具有兩個(gè)明(míng)顯的(de)特征：

Peters 将源于自然科學的(de)重标極差（R/S）方法和(hé) Hurst 指數（Hurst 1951）運用(yòng)到經濟系統。R/S 方法通(tōng)過計算(suàn) Hurst 指數有效地描繪不同頻(pín)率上收益率序列在各階矩上的(de)自相似性的(de)大(dà)小。Hurst 指數的(de)取值在 0 到 1 之間。0.5 說明(míng)時(shí)間序列是完全随機的(de)；當 Hurst 指數在 0.5 到 1 之間時(shí)，說明(míng)該序列有一定的(de)長(cháng)期正相關性，表示時(shí)間序列如果當前的(de)數值比較大(dà)（或小），那麽接下(xià)來(lái)出現的(de)數值也(yě)可(kě)能比較大(dà)（或小）；當 Hurst 指數在 0 到 0.5 之間時(shí)，說明(míng)該序列的(de)數值可(kě)能較大(dà)較小交替出現。

分(fēn)形市場(chǎng)假說在歐美(měi)和(hé)我國股市都得(de)到了(le)很多(duō)實證的(de)支持。有很多(duō)券商的(de)報告中利用(yòng) Hurst 指數描繪股價走勢是否有趨勢性或者反轉性，并以此開發擇時(shí)策略。此外，在分(fēn)形的(de)基礎上又發展出來(lái)了(le)多(duō)重分(fēn)形，來(lái)更好的(de)刻畫(huà)資本市場(chǎng)的(de)非線性動态特征。在這(zhè)些方面，我們也(yě)都做(zuò)了(le)大(dà)量的(de)研究，會在今後的(de)專題中繼續介紹。

參考文獻

Hurst, H. E. (1951). Long-term storage capacity of reservoirs. Transactions of American Society of Civil Engineers 116(1), 770 – 799

Mandelbrot, B. B. (1977). Fractals: form, chance and dimension. San Francisco: Freeman.

Mandelbrot, B. B. (1982). The fractal geometry of nature. New York: Freeman.

Peters, E. E. (1994). Fractal market analysis: applying chaos theory to investment and economics. New York: Wiley.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。