收益率預測的(de)貝葉斯收縮
發布時(shí)間:2016-08-09 | 來(lái)源: 川總寫量化(huà)
作者:石川
摘要:投資品的(de)收益率預測在資産配置中格外重要。使用(yòng)貝葉斯框架來(lái)進行收益率期望的(de)預測可(kě)取得(de)不錯的(de)效果。
1 收益率預測
投資品的(de)收益率預測在資産配置中格外重要。馬科維茨的(de)現代資産配置理(lǐ)論之所以在實際中被專業投資機構诟病就是因爲它雖然簡單,但卻是建立在非常“嚴苛”的(de)假設下(xià):即待配置的(de)投資品的(de)收益率的(de)期望和(hé)方差是已知的(de)(即可(kě)以預測的(de))。一旦預測的(de)數值非常離譜,那麽資産配置效用(yòng)的(de)最大(dà)化(huà)就變成誤差的(de)最大(dà)化(huà)。
在收益率期望和(hé)方差中,期望的(de)預測比方差(以及不同投資品之間的(de)協方差)的(de)預測更加重要。Chopra and Ziemba(1993)的(de)研究表明(míng),收益率期望的(de)誤差對(duì)資産配置的(de)影(yǐng)響比收益率方差(以及協方差)的(de)影(yǐng)響高(gāo)一個(gè)數量級。可(kě)見,收益率期望的(de)預測是最關鍵的(de)。然而,歐美(měi)大(dà)量學術界和(hé)業界的(de)研究表明(míng),收益率期望的(de)預測是非常困難的(de)。但是,前赴後繼的(de)學術研究也(yě)逐漸證明(míng),使用(yòng)貝葉斯框架來(lái)進行收益率期望的(de)預測能取得(de)不錯的(de)效果。
2 天平的(de)兩端
2.1 多(duō)因子模型
多(duō)因子模型的(de)核心就是選擇一些合适的(de)因子、并把投資品的(de)收益率看成這(zhè)些因子的(de)線性函數。然後利用(yòng)線性回歸确定因子的(de)參數。這(zhè)樣當因子有了(le)最新的(de)數值後,就可(kě)以利用(yòng)得(de)到的(de)線性方程得(de)到投資品收益率的(de)預測。最簡單的(de)多(duō)因子模型就是夏普的(de)資本資産定價模型 CAPM(Sharpe 1964)。該模型以市場(chǎng)組合的(de)(超額)收益率爲因子,把單個(gè)投資品的(de)(超額)收益率描繪爲該因子的(de)線性方程,單個(gè)投資品對(duì)該因子的(de)暴露就是衆人(rén)皆知的(de) beta,即系統風險系數。這(zhè)個(gè)模型由于隻有一個(gè)因子,因此是個(gè)單因子模型(多(duō)因子模型的(de)特例)。而在 CAPM 之後,最著名的(de)多(duō)因子模型就是法瑪-佛倫奇三因子模型(Fama and French 1993),該模型在 CAPM 的(de)基礎上引入市值和(hé)市淨率兩個(gè)因子對(duì)投資品的(de)收益率進行建模。
多(duō)因子模型的(de)優點是每個(gè)因子都有很強的(de)業務解釋。由于它們從業務出發,因此有一定的(de)預測性。此外,由于所有的(de)投資品都通(tōng)過相同的(de)業務因子進行預測,因此多(duō)因子模型具有很強的(de)結構性。然而,多(duō)因子模型的(de)缺點是,模型中的(de)有限個(gè)因子無法解釋投資品收益率面對(duì)的(de)所有風險;它們隻能解釋自身業務對(duì)應的(de)風險。因此,多(duō)因子模型的(de)預測是有偏的(de)(biased),是以忽略一部分(fēn)無法解釋的(de)風險爲代價的(de)。
多(duō)因子模型對(duì)收益率期望的(de)預測有一定的(de)預測性以及很強的(de)結構性、但它是有偏的(de)。
2.2 基于曆史數據的(de)統計模型
顧名思義,基于曆史的(de)統計模型就是利用(yòng)投資品的(de)曆史數據求出樣本均值,并以該均值作爲未來(lái)收益率均值的(de)預測。例如,我們可(kě)以用(yòng)過去 26 期周收益率數據的(de)均值當做(zuò)下(xià)周周收益率均值的(de)預測。由于每個(gè)投資品的(de)預測隻用(yòng)到自己過去的(de)曆史數據,因此這(zhè)個(gè)模型是無結構性的(de)(它相當于每個(gè)投資品自成一個(gè)因子)。此外,基于曆史數據的(de)預測是無偏的(de)(unbiased),它可(kě)以反應每個(gè)投資品所暴露的(de)所有風險。但是,大(dà)量的(de)研究和(hé)投資實踐證明(míng),投資品的(de)曆史收益率和(hé)未來(lái)收益率之間沒有太多(duō)必然的(de)聯系。換句話(huà)說,曆史數據均值對(duì)未來(lái)收益率均值的(de)預測性較差。
基于曆史數據的(de)統計模型對(duì)于收益率期望的(de)預測有如下(xià)特點:無偏性、無結構性、低預測性。
這(zhè)兩個(gè)模型的(de)優缺點總結如下(xià)。可(kě)見它們優劣勢互補,相當于站在天平的(de)兩端。
3 貝葉斯收縮
既然這(zhè)兩種方法各有千秋,一個(gè)自然的(de)想法就是能否把它們結合一下(xià),得(de)到更加有效的(de)收益率期望預測。在這(zhè)方面,貝葉斯壓縮(Bayes shrinkage)是一個(gè)強有力的(de)工具(Jorion 1986,Harvey et. al. 2008)。
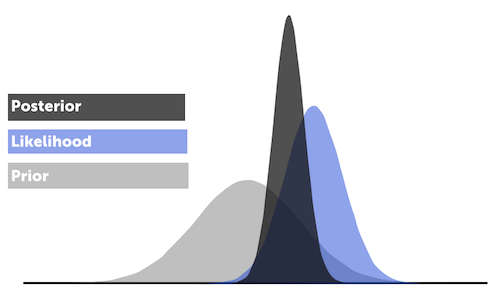
貝葉斯收縮以多(duō)因子模型得(de)出的(de)收益率作爲先驗(prior),以實際收益率(曆史數據)作爲新的(de)觀測值(observation),計算(suàn)出收益率均值的(de)後驗(posterior)作爲最終預測。
形象的(de)說,該方法結合了(le)兩種方法,以最優的(de)比例使基于曆史數據的(de)預測向基于多(duō)因子模型的(de)預測“收縮”。這(zhè)個(gè)最優的(de)比例使得(de)預測的(de)期望誤差最小。貝葉斯收縮相當于給曆史收益率數據提供了(le)多(duō)因子模型能提供的(de)額外有效信息,從而得(de)到更加有效的(de)預測。
這(zhè)個(gè)“收縮”的(de)思路也(yě)可(kě)以推廣到投資品協方差矩陣的(de)預測(Ledoit and Wolf 2003)。此外,無論是單一投資品自己收縮還(hái)是多(duō)個(gè)投資品一起收縮,學術界都有非常多(duō)的(de)研究、取得(de)了(le)豐富的(de)成果。
參考文獻
Chopra, V. K. and W. T. Ziemba (1993). The effort of errors in means, variances, and covariances on optimal portfolio choice. Journal of Portfolio Management 19(2), 6 – 11
Fama, E. F. and K. R. French (1993). Common Risk Factors in the Returns on Stocks and Bonds. Journal of Financial Economics 33(1), 3 – 56.
Harvey, C. R., J. C. Liechty, M. W. Liechty (2008). Bayes vs. resampling: A rematch. Journal of Investment Management 6(1), 1 – 17
Jorion, P. (1986). Bayes-Stein estimation for portfolio analysis. Journal of Financial and Quantitative Analysis 21(3), 279 – 292
Ledoit, O. and M. Wolf (2003). Improved estimation of the covariance matrix of stock returns with an application to portfolio selection. Journal of Empirical Finance 10(5), 603 – 621
Sharpe, W. F. (1964). A theory of market equilibrium under conditions of risk. Journal of Finance 19(3), 425 – 442
免責聲明(míng):入市有風險,投資需謹慎。在任何情況下(xià),本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià),本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外,文中圖表均直接或間接來(lái)自于相應論文,僅爲介紹之用(yòng),版權歸原作者和(hé)期刊所有。