Which Beta (III) ?

發布時(shí)間：2021-06-07 | 來(lái)源: 川總寫量化(huà)

作者：石川

摘要：若市場(chǎng)中不（持續）存在無風險套利機會，那麽資産的(de)預期收益由資産和(hé)因子的(de)協方差（即 $\beta$ ）決定。

最近我被 Stefan Nagel 圈粉。

Stefan Nagel 何許人(rén)也(yě)？他(tā)是芝加哥(gē)大(dà)學的(de)金融學教授，Journal of Finance 的(de)執行主編，尤其擅長(cháng)資産定價理(lǐ)論。我最近接連精讀了(le)他(tā)的(de)兩篇文章(zhāng)，它們均很好地補充了(le)我對(duì)資産定價和(hé)因子投資的(de)理(lǐ)解。因此本文和(hé)兩周後的(de)文章(zhāng)将會背靠背介紹這(zhè)兩篇文章(zhāng)。

今天要說的(de)是 Kozak, Nagel, and Santosh (2018)，标題是 Interpreting Factor Models（下(xià)稱 KNS）。早在 2015 年，該文就出現在 AFA 年會上，後來(lái) 2017 年被 Journal of Finance 接收，2018 年見刊。該文是資産定價理(lǐ)論和(hé)實證數據的(de)完美(měi)結合，加深了(le)人(rén)們對(duì) reduced-form factor models（即多(duō)因子模型）的(de)理(lǐ)解。

爲了(le)說明(míng) KNS 的(de)核心結論，先來(lái)定義一下(xià)無風險套利機會。該文将其定義爲“trading strategies that earn extremely high Sharpe ratios”（即超高(gāo)夏普率的(de)交易策略）。這(zhè)句話(huà)可(kě)以被更精确地解讀爲兩點：（1）超高(gāo)夏普率可(kě)以在短時(shí)内存在，但不是持續的(de)現象；（2）超高(gāo)夏普率策略無法産生巨大(dà)的(de)價格沖擊（can't have large price impact）。和(hé)人(rén)們的(de)認知相符，市場(chǎng)上難以存在同時(shí)不滿足以上兩點的(de)無風險套利機會。

假設市場(chǎng)中不存在上述定義的(de)無風險套利機會，KNS 的(de)兩個(gè)核心結論（順序分(fēn)先後，但是同等重要）如下(xià)：

1. 資産的(de)預期超額收益由資産和(hé)因子的(de)協方差（也(yě)就是我們常說的(de) $\beta$ ）決定，而這(zhè)些因子和(hé)資産收益率的(de)協方差矩陣密切相關。關于前半句話(huà)，根據定義， $\beta$ 是資産收益率對(duì)因子收益率的(de)回歸系數，而回歸系數的(de)分(fēn)子就是二者的(de)協方差[1]。這(zhè)個(gè)結論給近年來(lái)的(de) covariance 和(hé) firm characteristics 到底哪個(gè)能決定資産預期收益之争提供了(le)非常重要的(de)啓發（這(zhè)也(yě)是爲什(shén)麽本文的(de)标題爲 Which Beta (III) ?）。

2. 盡管資産預期收益由 $\beta$ 決定，但僅從這(zhè)點出發，人(rén)們并不能區(qū)分(fēn)因子背後是風險補償解釋還(hái)是錯誤定價解釋。換句話(huà)說，哪怕資産的(de)價格僅僅由非理(lǐ)性投資者持有的(de)關于資産收益分(fēn)布的(de)失真信仰決定，資産的(de)預期收益依然由資産和(hé)因子的(de)協方差（ $\beta$ ）決定。

由上述第一點可(kě)知，在 KNS 的(de)研究視角下(xià)，多(duō)因子模型中的(de)因子并非像 Fama and French (1993) 三因子（FF3）模型這(zhè)樣給定的(de) MKT、HML 以及 SMB 因子，而是從資産收益率的(de)協方差矩陣出發，通(tōng)過 PCA 構造的(de)因子。爲此，在實證研究中，KNS 選擇了(le)兩組 test assets。第一組是 Novy-Marx and Velikov (2016) 一文提及的(de) 15 個(gè)代表性異象的(de)各自多(duō)、空組合（因此一共 30 個(gè) test assets）；第二組是 FF3 使用(yòng)的(de) size-B/M 雙重排序構造的(de) 25 個(gè)投資組合。

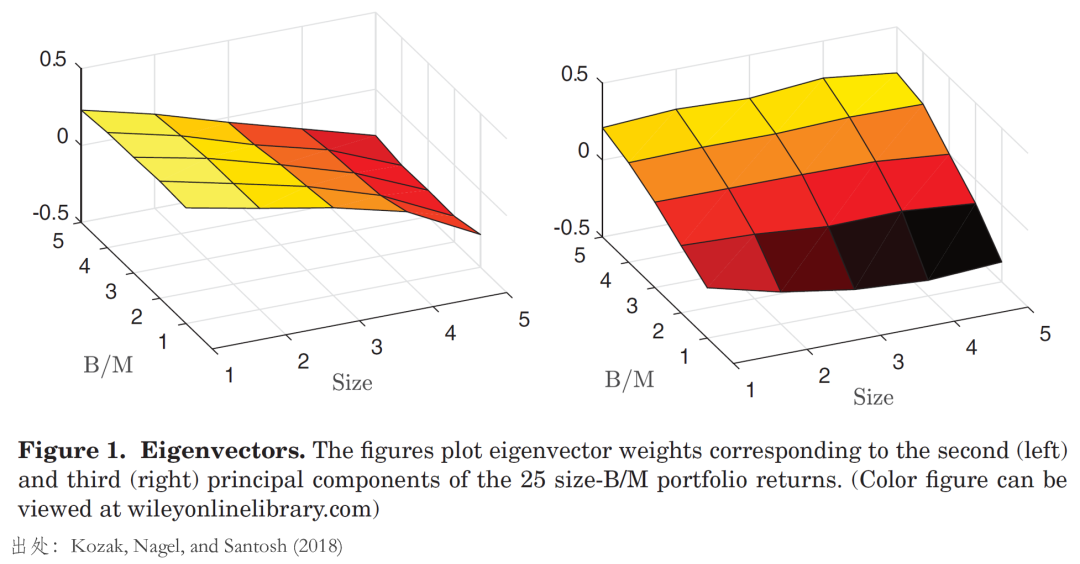
看到這(zhè)裏有小夥伴可(kě)能會問，使用(yòng) PCA 構造的(de)因子是否有足夠的(de)經濟學含義。以 FF3 的(de) 25 個(gè) test assets 爲例，對(duì)它們進行 PCA 運算(suàn)，得(de)到的(de)第一主成分(fēn)可(kě)以被理(lǐ)解爲一個(gè) level factor，正好對(duì)标 MKT，而第二、三主成分(fēn)中 test assets 的(de)權重如下(xià)圖所示。

從上面左圖不難看出，test assets 的(de)權重随著(zhe) size quartiles 逐漸降低（其中小市值組合的(de)權重爲正，大(dà)市值組合的(de)權重爲負），且每個(gè) size 下(xià)不同 B/M 組合的(de)權重很接近，這(zhè)毫無疑問對(duì)應了(le) FF3 中的(de) SMB。另一方面，右圖顯示 test assets 的(de)權重随 B/M quartiles 逐漸升高(gāo)（其中高(gāo) B/M 組合權重爲正，低 B/M 組合權重爲負），且給定 B/M 下(xià)不同 size 組合的(de)權重接近，這(zhè)無疑對(duì)應了(le) FF3 的(de) HML。

這(zhè)個(gè)例子清晰的(de)說明(míng)，當 test assets 中有很強的(de) factor structures，那麽 PCA 是注定能夠識别它們的(de)。而在這(zhè)個(gè)例子中，對(duì)于這(zhè) 25 個(gè) test assets 來(lái)說，利用(yòng)前三個(gè)主成分(fēn)構造的(de)多(duō)因子模型就完全對(duì)标了(le) FF3。因此，像 FF3 這(zhè)種人(rén)爲構造的(de)因子并無特殊性，而使用(yòng) PCA 構造的(de)因子則更具一般性。

對(duì)于給定的(de) test assets，PCA 雖然能夠從它們的(de)協方差矩陣中構造出因子，但人(rén)們真正關心的(de)問題是，資産和(hé)這(zhè)些因子的(de)協方差（ $\beta$ ）能否決定資産的(de)預期收益呢(ne)？KNS 通(tōng)過資産定價理(lǐ)論分(fēn)析表明(míng)，在市場(chǎng)中不存在無風險套利機會的(de)假設下(xià)，上述問題的(de)答(dá)案是肯定的(de)。

假設共有 $N$ 個(gè)資産，令 $R$ 表示它們的(de)超額收益， $\mu\equiv\mbox{E}[R]$ 表示它們的(de)預期超額收益， $\Gamma$ 表示 $R$ 的(de)協方差矩陣。由于 $R$ 是超額收益，因此存在随機折現因子（SDF） $M$ 使得(de) $\mbox{E}[MR]=0$ 。根據 Hansen and Jagannathan (1991) 的(de)研究， $M$ 可(kě)以表示爲以下(xià)形式：

$M=1-\mu^\prime\Gamma^{-1}(R-\mu)$

由于 $R$ 是超額收益，因此 $M$ 可(kě)以被任意縮放。爲方便推導，不妨令 $\mbox{E}[M]=1$ ，由此可(kě)以推導出 $M$ 的(de)方差爲：

$\mbox{var}(M)=\mu^\prime\Gamma^{-1}\mu$

換句話(huà)說，随機折現因子 $M$ 的(de)方差由通(tōng)過 $N$ 個(gè)資産構造的(de)最大(dà)夏普率的(de)平方（squared SR）決定。“ $\mbox{var}(M)=\mbox{squared SR}$ ”這(zhè)個(gè)關系将在稍後的(de)分(fēn)析中發揮重要的(de)作用(yòng)。

爲了(le)進一步分(fēn)析，對(duì)資産的(de)協方差矩陣 $\Gamma$ 進行特征分(fēn)解，得(de)到 $\Gamma=Q\Lambda Q^\prime$ ，其中 $\Lambda$ 是對(duì)角陣，對(duì)角線上的(de)元素爲特征值 $\lambda_k$ ，而 $Q=(q_1,\cdots,q_N)$ 的(de)每一列爲一個(gè)特征向量。KNS 進一步假設第一主成分(fēn)是一個(gè) level factor，而從第二主成分(fēn)開始，它們都代表了(le)由 $N$ 個(gè)資産構造的(de)某種 long-short portfolios。

帶著(zhe)上述 PCA 分(fēn)解，再來(lái)看 $\mbox{var}(M)$ 。由數學推導可(kě)知：

$\displaystyle\mbox{var}(M)=\frac{\mu_m^2}{\sigma_m^2}+N\overline{\mbox{var}}(\mu_i)\sum_{k=2}^N\frac{\overline{\mbox{corr}}(\mu_i,q_{ki})^2}{\lambda_k}$

其中第一項和(hé) level factor 有關，我們主要來(lái)看第二項。第二項是剩餘 $N-1$ 個(gè)主成分(fēn)求和(hé)，而它的(de)大(dà)小取決于每一項中分(fēn)子和(hé)分(fēn)母的(de)大(dà)小，其中分(fēn)子是每個(gè)資産的(de)預期收益和(hé)某個(gè)主成分(fēn)的(de)截面相關系數（的(de)平方），而分(fēn)母是該主成分(fēn)對(duì)應的(de)特征值。

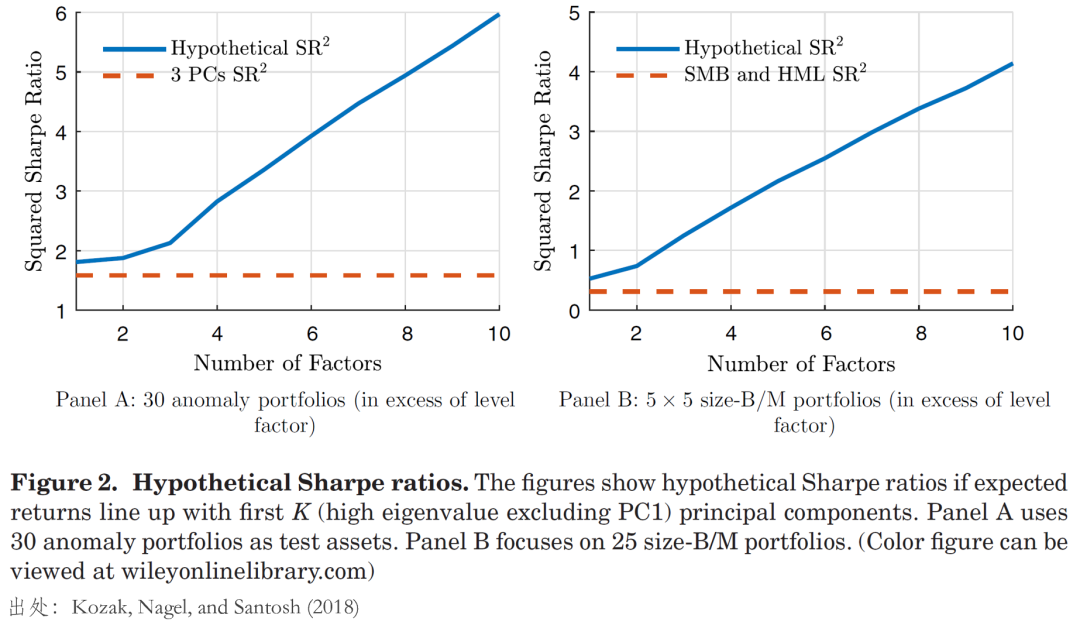
接下(xià)來(lái)，就是最重要的(de)推斷。大(dà)量實證數據表明(míng)，對(duì)資産收益率協方差矩做(zuò) PCA 分(fēn)解時(shí)，特征值衰減的(de)是非常快(kuài)的(de)。這(zhè)意味著(zhe)除了(le)前幾個(gè)主成分(fēn)外，後面主成分(fēn)的(de)特征值非常小。如果資産的(de)預期收益 $\mu_i$ 和(hé)後面的(de)主成分(fēn)（higher order PCs）高(gāo)度相關，由于它們的(de)特征值（ $\lambda_k$ ）很低，這(zhè)将造成上式中的(de)第二項很大(dà)，因而 $\mbox{var}(M)$ 很大(dà)。而從之前的(de)推導可(kě)知， $\mbox{var}(M)$ 等于 $N$ 個(gè)資産構造的(de)最大(dà) squared SR，因此我們可(kě)以推出：如果資産的(de)預期收益 $\mu_i$ 和(hé) higher order PCs 高(gāo)度相關（而和(hé)前幾個(gè)主成分(fēn)不相關），則由 $N$ 個(gè)資産構造的(de)最大(dà) squared SR 就會非常大(dà)，即市場(chǎng)中存在無風險套利的(de)機會。由于市場(chǎng)中不存在無風險套利機會，因此反過來(lái)：在市場(chǎng)中不存在無風險套利機會（即最大(dà) squared SR 是有限）的(de)假設下(xià)，資産的(de)預期收益就必須和(hé)前幾個(gè)主成分(fēn)高(gāo)度相關。

利用(yòng)本文開篇提到了(le)兩組 test assets，KNS 給出了(le)上述結論的(de)實證證據。如下(xià)圖所示，對(duì)于這(zhè)兩組 test assets，如果這(zhè)些資産的(de)預期收益和(hé)更多(duō)的(de) higher order 主成分(fēn)高(gāo)度相關，則最大(dà)的(de) squared SR 是非常高(gāo)的(de)。例如，對(duì)于第一組 test assets，如果它們和(hé)前 10 個(gè)主成分(fēn)都高(gāo)度相關，則它們構造的(de)最大(dà) squared SR 将高(gāo)達 6.0，這(zhè)顯然和(hé)真實情況不符，所以資産的(de)預期收益隻能和(hé)前幾個(gè)主成分(fēn)相關。

前文的(de)論述表明(míng)資産預期收益和(hé)前幾個(gè)主成分(fēn)高(gāo)度相關，即對(duì)前幾個(gè)主成分(fēn)來(lái)說 $\overline{\mbox{corr}}(\mu_i,q_{ki})^2$ 很大(dà)。但從這(zhè)個(gè)現象還(hái)無法直接推出資産和(hé)這(zhè)些 PCA 因子的(de)協方差（ $\beta$ ）能夠解釋資産的(de)預期收益。因此，爲了(le)考察這(zhè)一點，KNS 使用(yòng) PCA 構造的(de)多(duō)因子模型，通(tōng)過時(shí)序分(fēn)析進行了(le)實證研究。以 Novy-Marx and Velikov (2016) 中涉及的(de) 15 個(gè)異象爲例，下(xià)表展示了(le) PCA 因子模型的(de)定價能力。對(duì)于絕大(dà)多(duō)數異象來(lái)說，随著(zhe)因子個(gè)數的(de)增加，異象的(de)定價誤差逐漸降低，說明(míng)資産和(hé)這(zhè)些因子的(de) $\beta$ 能夠很好的(de)解釋它們的(de)預期收益。

綜合前述所有模型推論和(hé)實證結果，我們可(kě)以得(de)出結論：資産收益率波動的(de)共性由若幹個(gè)因子主宰，資産預期收益率和(hé)這(zhè)些因子密切相關（ $\overline{\mbox{corr}}(\mu_i,q_{ki})^2$ 大(dà)），資産預期收益率的(de)截面差異由資産和(hé)因子的(de)協方差（ $\beta$ ）決定。在這(zhè)個(gè)結論下(xià)，如果投資者想要獲取例如低估值 vs 高(gāo)估值或者赢家 vs 輸家股票(piào)之間預期收益的(de)差異，就必須要承擔在相應因子上必要的(de)暴露。

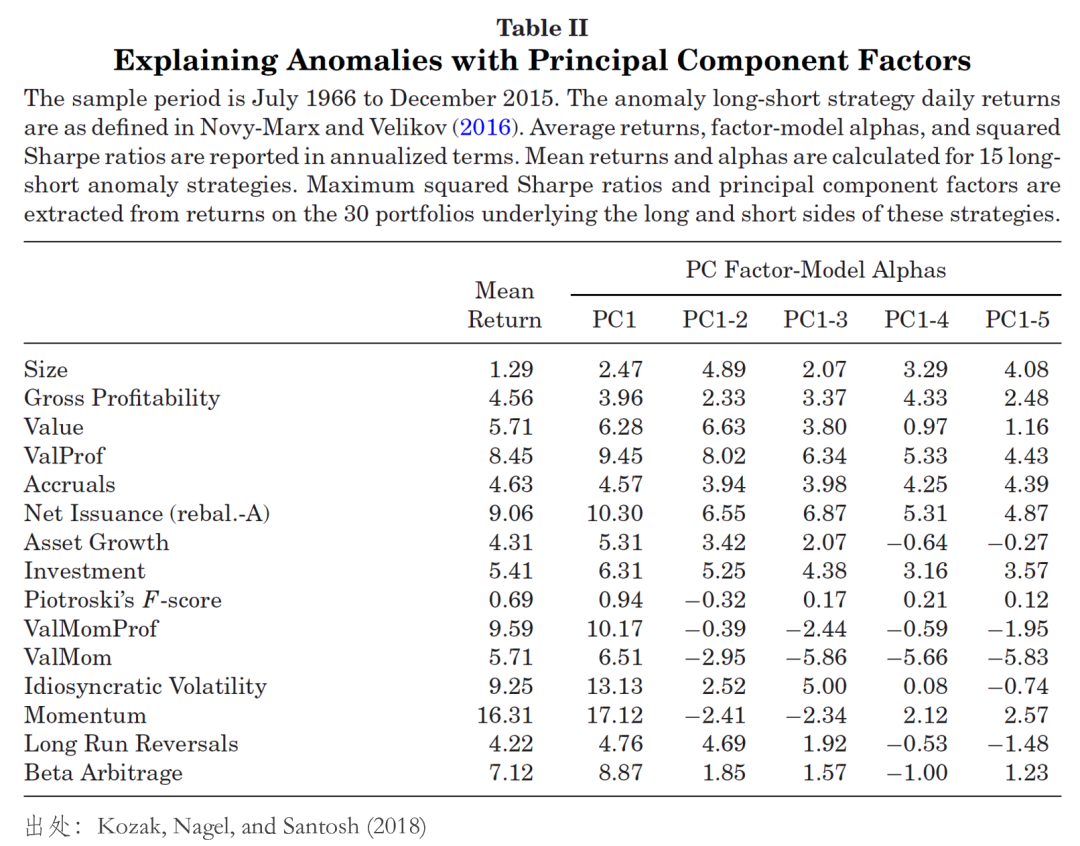
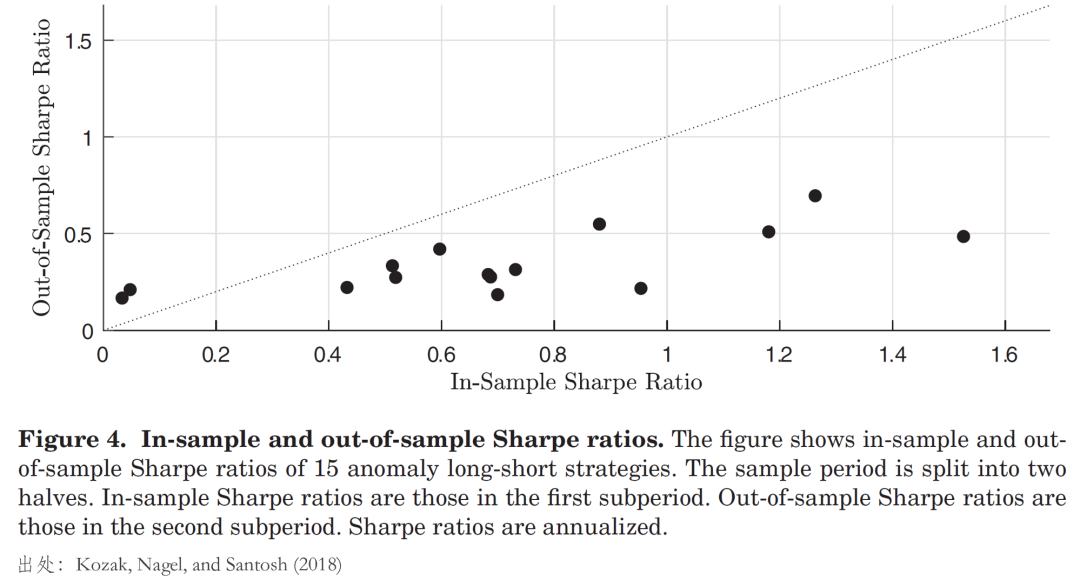
盡管如此，上述結論也(yě)并非沒有受到其他(tā)實證結果的(de)沖擊。在諸多(duō)實證挑戰中，最有代表性的(de)無疑還(hái)是要數“which beta”[2]之争。Daniel and Titman (1997) 研究了(le) FF3 并發現資産的(de)預期收益由 size 和(hé) B/M 這(zhè)些 firm characteristics 決定，而非 $\beta$ 決定[3]。放在 KNS 的(de)理(lǐ)論框架下(xià)，由于主成分(fēn)之間的(de)是正交的(de)，這(zhè)意味著(zhe) Daniel and Titman (1997) 主張預期收益和(hé) higher order PCs 相關。這(zhè)顯然和(hé) KNS 的(de)結論背道而馳。

另一方面，僅看 KNS 自己的(de)實證結果，以第一組 30 個(gè) test assets 爲例，它們構造的(de)事後（ex post）最大(dà) squared SR 高(gāo)達 4.23，而前五個(gè)主成分(fēn)構造的(de)最大(dà) squared SR 僅爲 1.77。這(zhè)兩個(gè)數字之間巨大(dà)的(de)鴻溝似乎也(yě)表明(míng)還(hái)有一些 higher order PCs 決定了(le)預期收益。但事實真的(de)如此嗎？對(duì)于這(zhè)一點，KNS 給出了(le)至少在我看來(lái)合情合理(lǐ)的(de)解釋。而解釋的(de)關鍵就在于所謂高(gāo) squared SR 在跨越樣本内外的(de)可(kě)持續性。仍以 Novy-Marx and Velikov (2016) 的(de)異象爲例，如果将實證區(qū)間一分(fēn)爲二，前半部分(fēn)爲樣本内（IS），後半部分(fēn)爲樣本外（OOS），并繪制出他(tā)們在樣本内外的(de)夏普率（下(xià)圖）。可(kě)以看到，在實證區(qū)間的(de)後半段，幾乎所有異象的(de)夏普率都低于前半段。

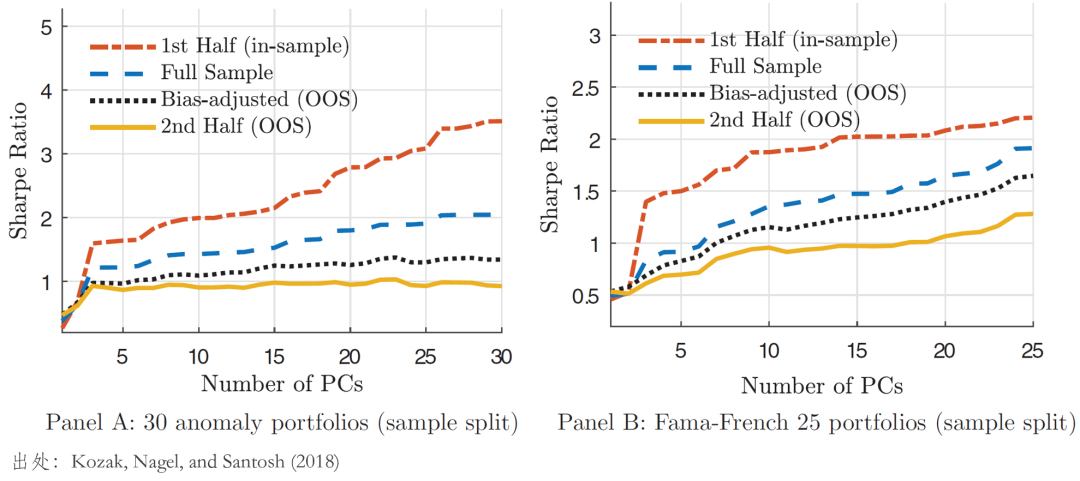
此外，利用(yòng)上述劃分(fēn)，KNS 使用(yòng)前半段樣本内數據構造了(le)主成分(fēn)，并檢驗主成分(fēn)所實現的(de)最大(dà) squared SR 在樣本内外的(de)差異，結果如下(xià)圖所示。

無論是針對(duì)哪一組 test assets，上述結果清晰的(de)顯示出：在樣本内，夏普率随主成分(fēn)數量單調遞增，然而在樣本外，夏普率随著(zhe)主成分(fēn)個(gè)數的(de)增加卻提升的(de)非常緩慢(màn)（且對(duì)于給定個(gè)數的(de)主成分(fēn)，樣本外夏普率比樣本内低的(de)多(duō)）。樣本内外的(de)差異表明(míng)，哪怕事後來(lái)看一些 higher order PCs 能夠決定資産預期收益，它們也(yě)很難在樣本外維系。這(zhè)個(gè)結果從一定程度上回應了(le) Daniel and Titman (1997) 的(de)發現。

There are additional reasons to suspect that high ex-post SRs are not robust indicators of persistent near-arbitrage opportunities. Short-lived near-arbitrage opportunities might exist for a while before being recognized and eliminated by arbitrageurs. Data-snooping biases further overstate in-sample SRs.

再回到 covariance 和(hé) characteristics 之争。從行爲金融學角度來(lái)說，人(rén)們認爲 characteristics 而非 covariance 決定資産定價；這(zhè)種“非理(lǐ)性”定價行爲也(yě)被認爲是和(hé) covariance 正交的(de)定價錯誤。然而，事實真的(de)如此嗎？爲了(le)從直覺上理(lǐ)解這(zhè)個(gè)問題，我們用(yòng)人(rén)們喜聞樂(yuè)見的(de)截面動量來(lái)說明(míng)。行爲金融學認爲動量背後的(de)原因是定價錯誤，不能被資産和(hé)前幾個(gè)主成分(fēn)的(de) covariance（即 $\beta$ ）解釋。如果這(zhè)個(gè)結論是對(duì)的(de)，它意味著(zhe)動量必然和(hé) higher order PCs 有關。然而實證數據顯示，截面動量的(de)多(duō)頭和(hé)空頭内的(de)股票(piào)都有很強的(de)共同運動。由于股票(piào)的(de)共同運動很大(dà)程度上由前幾個(gè)主成分(fēn)解釋，而非 higher order PCs，因此該觀點和(hé)實證數據不符。

在套利者看來(lái)，上述共同運動代表了(le)某種他(tā)們不願意去交易的(de)系統性風險，也(yě)正因如此動量多(duō)空兩頭的(de)收益率才有差異、動量才被定價。如果像行爲金融學的(de)看法那樣，截面動量中的(de)股票(piào)沒有共同運動（即沒有系統性風險），而是和(hé) higher order PCs 有關（即是由特質性波動造成的(de)），那麽對(duì)套利者來(lái)說這(zhè)将是獲得(de)無風險套利的(de)絕佳機會，他(tā)們會充分(fēn)套利，導緻動量的(de)收益不複存在。

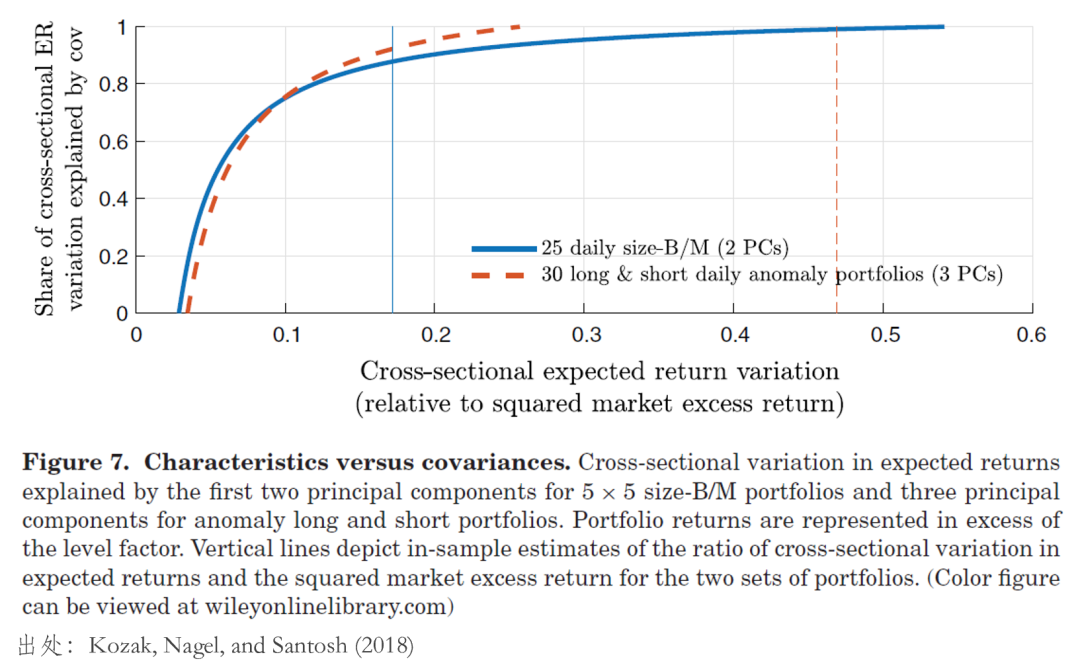
離開這(zhè)個(gè)例子之前，最後需要澄清的(de)一點是：動量背後本身的(de)原因完全可(kě)以是來(lái)自行爲金融學（上述討(tǎo)論完全不否認這(zhè)一點）；但我們希望這(zhè)個(gè)例子強調的(de)是，正如 KNS 研究的(de)第二部分(fēn)表明(míng)，即便資産的(de)定價完全由非理(lǐ)性交易者驅動，它們的(de)預期收益依然由（資産和(hé)因子的(de)）協方差（ $\beta$ ）決定。爲了(le)得(de)到定量的(de)推斷，KNS 在模型中考慮市場(chǎng)中存在理(lǐ)性交易者和(hé)情緒交易者。相較于前者，情緒交易者對(duì)資産的(de)需求多(duō)了(le)一個(gè)參數 $\delta$ 。此外，考慮到現實世界中情緒交易者的(de)實際約束（例如不能毫無限制的(de)使用(yòng)杠杆或者做(zuò)空），因此在模型中， $\delta$ 滿足 $\delta^\prime\delta\le 1$ 的(de)約束。這(zhè)個(gè)條件是 KNS 和(hé)早期類似的(de)模型（例如 Daniel, Hirshleifer, and Subrahmanyam 2001）的(de)最大(dà)差異。

利用(yòng)該模型，KNS 討(tǎo)論了(le)很多(duō) implications。爲了(le)本文的(de)緊湊性（以及少放點公式），我挑一點來(lái)闡述。在該模型下(xià)，資産收益率相對(duì) CAPM 的(de)偏離完全由情緒交易者推動。如果按照(zhào)行爲金融學的(de)觀點，那麽應該是 characteristics 而非 covariance（ $\beta$ ）決定資産的(de)預期收益。然而，模型顯示，資産預期收益的(de)截面波動越高(gāo)，則這(zhè)些波動中被前幾個(gè)主成分(fēn)解釋的(de)比例也(yě)越高(gāo)（下(xià)圖）。

圖中給出了(le)兩組 test assets 上的(de)檢驗結果，其中豎直線表示了(le)真實數據中 test assets 預期收益的(de)截面波動（對(duì)于 FF3 的(de) 25 個(gè) test assets 是 0.17；另一組 30 個(gè) test assets 是 0.47）。圖中縱坐(zuò)标是截面波動中被前兩個(gè)（對(duì)于 FF3 的(de) test assets）和(hé)前三個(gè)（對(duì)于 30 個(gè) test assets）主成分(fēn)[4]能夠解釋的(de)比例。結果顯示，哪怕在這(zhè)個(gè)價格由情緒交易者驅動的(de)世界中，資産和(hé)前幾個(gè)主成分(fēn)的(de)協方差依然能在很大(dà)程度上解釋資産預期收益的(de)截面差異，而如果不采用(yòng)更進一步的(de)分(fēn)析，人(rén)們是無法區(qū)分(fēn)背後的(de)原因是風險補償還(hái)是非理(lǐ)性驅動的(de)定價錯誤。

以上是 KNS 中最核心的(de)觀點。該文還(hái)有其他(tā)一些很有價值的(de)討(tǎo)論，建議(yì)感興趣的(de)小夥伴去看原文。讀完此文，我也(yě)不禁思考，它對(duì)近年來(lái)的(de) which beta 之争以及因子投資有怎樣的(de)意義。首先，大(dà)量實證結果表明(míng)對(duì)于常見的(de)多(duō)因子模型來(lái)說，firm characteristics 似乎比 covariance 更能預測收益率。例如 Fama and French (2020) 的(de)研究也(yě)發現用(yòng) firm characteristics 的(de)動态模型比用(yòng) $\beta$ 的(de)靜态模型的(de)定價誤差更低[5]。這(zhè)些實證結果似乎和(hé) KNS 相悖。但是一方面，這(zhè)樣的(de)結果從一定程度上可(kě)以被前文討(tǎo)論的(de)樣本内外的(de)差異所解釋。另外，在這(zhè)個(gè)矛盾背後，我能想到的(de)另一個(gè)合理(lǐ)解釋就是，像諸如 SMB 和(hé) HML 這(zhè)些因子僅僅是構造 SDF 的(de)一小部分(fēn)（或者甚至不是組成 SDF 的(de)成分(fēn)），因而它們的(de)定價能力本身就很微弱，所以哪怕被 characteristics based test 拒絕了(le)，也(yě)不能說明(míng) KNS 的(de)結論有問題。從某種意義上來(lái)說，學術界的(de) covariance vs characteristics 之争可(kě)以理(lǐ)解爲人(rén)們在找尋能夠決定 mean-variance efficient frontier 組合的(de) characteristics[6]。而根據資産定價理(lǐ)論，一旦找到了(le)該組合，那麽資産的(de)預期收益就由資産和(hé)它的(de)協方差（ $\beta$ ）決定。

第二點就是 KNS 的(de)模型爲近年來(lái)流行的(de)行爲金融學多(duō)因子模型提供了(le)很好的(de)理(lǐ)論支持。無論是 Stambaugh and Yuan (2017) 還(hái)是 Daniel, Hirshleifer, and Sun (2020)，它們雖然都是從行爲金融學的(de)角度提出因子，然而最後用(yòng)來(lái)決定資産預期收益的(de)依然是資産和(hé)因子的(de)協方差（ $\beta$ ）。這(zhè)些實證結果和(hé) KNS 的(de)模型相符。最後，資産預期收益率由協方差（ $\beta$ ）決定也(yě)給一直以來(lái)的(de) $\alpha$ 和(hé) $\beta$ 之争很大(dà)的(de)啓示。按照(zhào)定義， $\alpha$ 代表了(le)無風險套利機會。無論是理(lǐ)論還(hái)是現實中， $\alpha$ 是不持久的(de)且無法造成大(dà)的(de)價格沖擊。而另一方面，KNS 的(de)模型表明(míng)，真正能夠決定資産預期收益率的(de)，唯有 $\beta$ 。

Kozak, Nagel, and Santosh (2018)，相見恨晚。

備注：

[1] 見《FF3 們背後的(de)資産定價理(lǐ)論》。

[2] 見《Which beta?》和(hé)《Which beta (II)?》。

[3] 這(zhè)篇文章(zhāng) 1997 年發表在 Journal of Finance 上，和(hé) Fama and French (1996) 隻相差 1 年，足見分(fēn)量。

[4] 除去第一個(gè) level factor 之外的(de)兩個(gè)和(hé)三個(gè)主成分(fēn)。

[5] 見《A new norm?》。

[6] 見《尋找 mean-variance frontier》。

參考文獻

Daniel, K. D., D. A. Hirshleifer, and A. Subrahmanyam (2001). Overconfidence, arbitrage, and equilibrium asset pricing. Journal of Finance 56(3), 921 – 965.

Daniel, K. D., D. A. Hirshleifer, and L. Sun (2020). Short- and long-horizon behavioral factors. Review of Financial Studies 33(4), 1673 – 1736.

Daniel, K. D. and S. Titman (1997). Evidence on the characteristics of cross sectional variation in stock returns. Journal of Finance 52(1), 1 – 33.

Fama, E. F. and K. R. French (1993). Common risk factors in the returns on stocks and bonds. Journal of Financial Economics 33(1), 3 – 56.

Fama, E. F. and K. R. French (1996). Multifactor explanations of asset pricing anomalies. Journal of Finance 51(1), 55 – 84.

Fama, E. F. and K. R. French (2020). Comparing cross-section and time-series factor models. Review of Financial Studies 33(5), 1891 – 1926.

Hansen, L. P. and R. Jagannathan (1991). Implications of security market data for models of dynamic economies. Journal of Political Economy 99(2), 225 – 262.

Kozak, S., S. Nagel, and S. Santosh (2018). Interpreting factor models. Journal of Finance 73(3), 1183 – 1223.

Novy-Marx, R. and M. Velikov (2016). A taxonomy of anomalies and their trading costs. Review of Financial Studies 29(1), 104 – 147.

Stambaugh, R. F. and Y. Yuan (2017). Mispricing factors. Review of Financial Studies 30(4), 1270 – 1315.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。

合格投資者聲明(míng)

Which Beta (III) ?