False In-Sample Predictability ?
發布時(shí)間:2021-06-22 | 來(lái)源: 川總寫量化(huà)
作者:石川
摘要:Martin and Nagel (2019) 指出投資者 high-dimensional learning 有可(kě)能造成樣本内虛假的(de)可(kě)預測性。
1
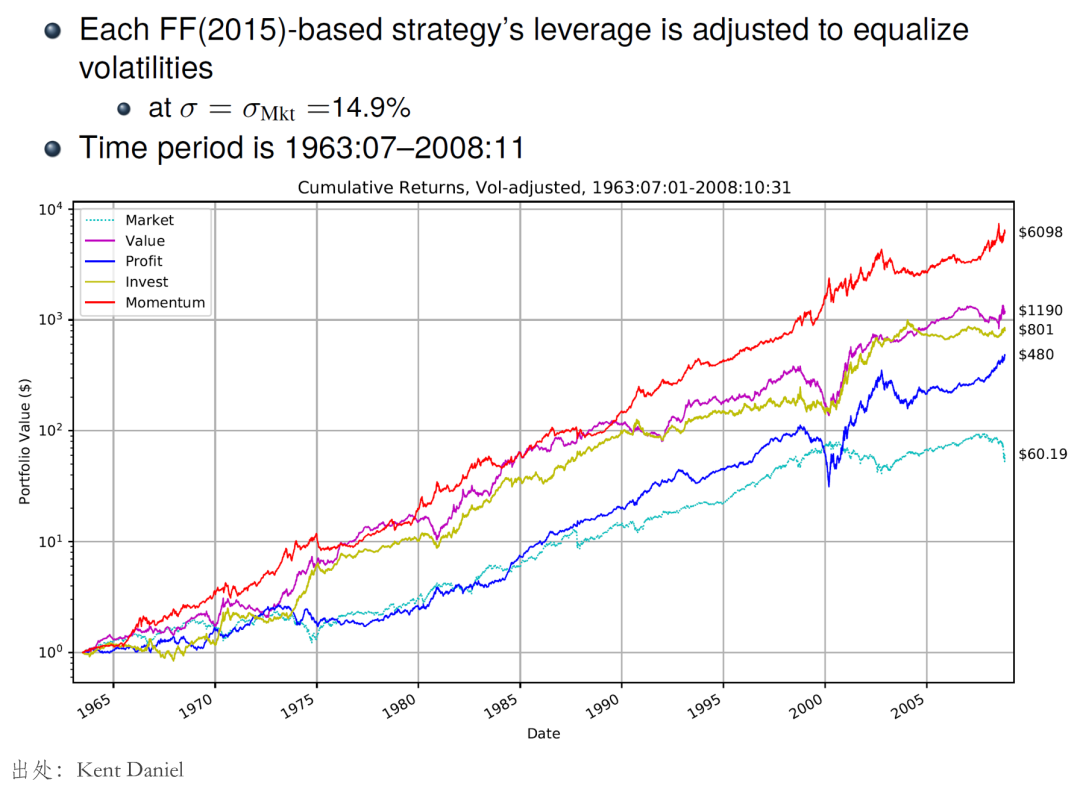
讓我們從兩組實證結果說起。下(xià)圖是 Fama and French (2015) 五因子(除了(le) SMB)和(hé) Carhart (1997) 動量因子在 1963 到 2008 年之間的(de)表現,無一例外的(de),它們都獲得(de)了(le)顯著的(de)超額收益。由于時(shí)間跨度和(hé)相關論文所涉及的(de)實證區(qū)間接近,我們可(kě)以把它們視作樣本内的(de)表現。
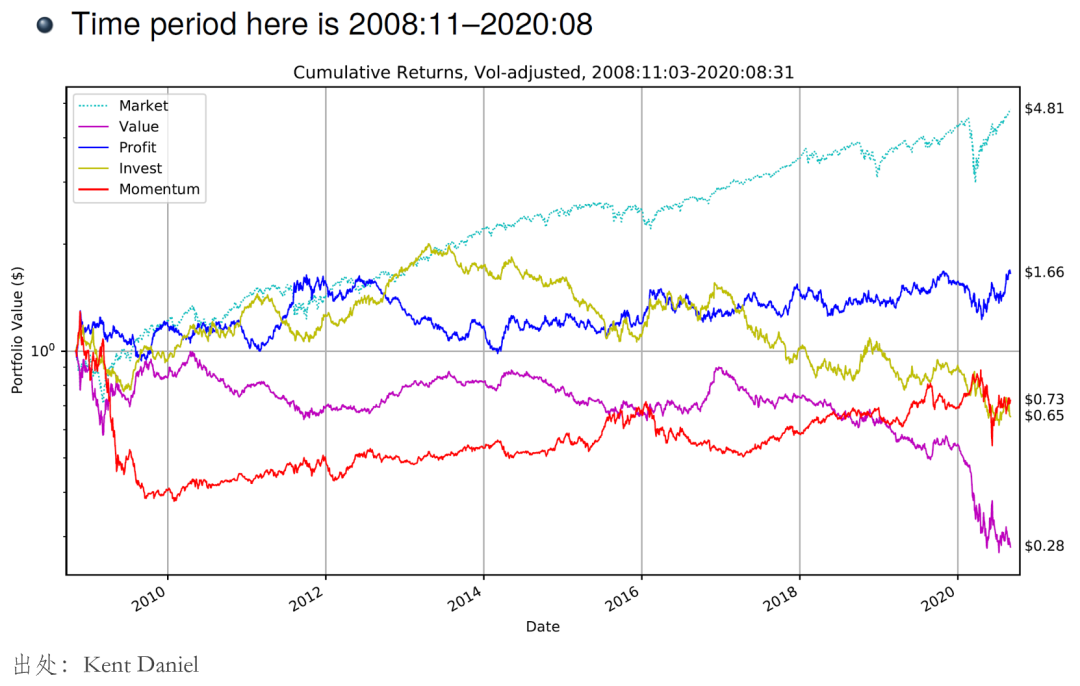
再來(lái)看看樣本外……
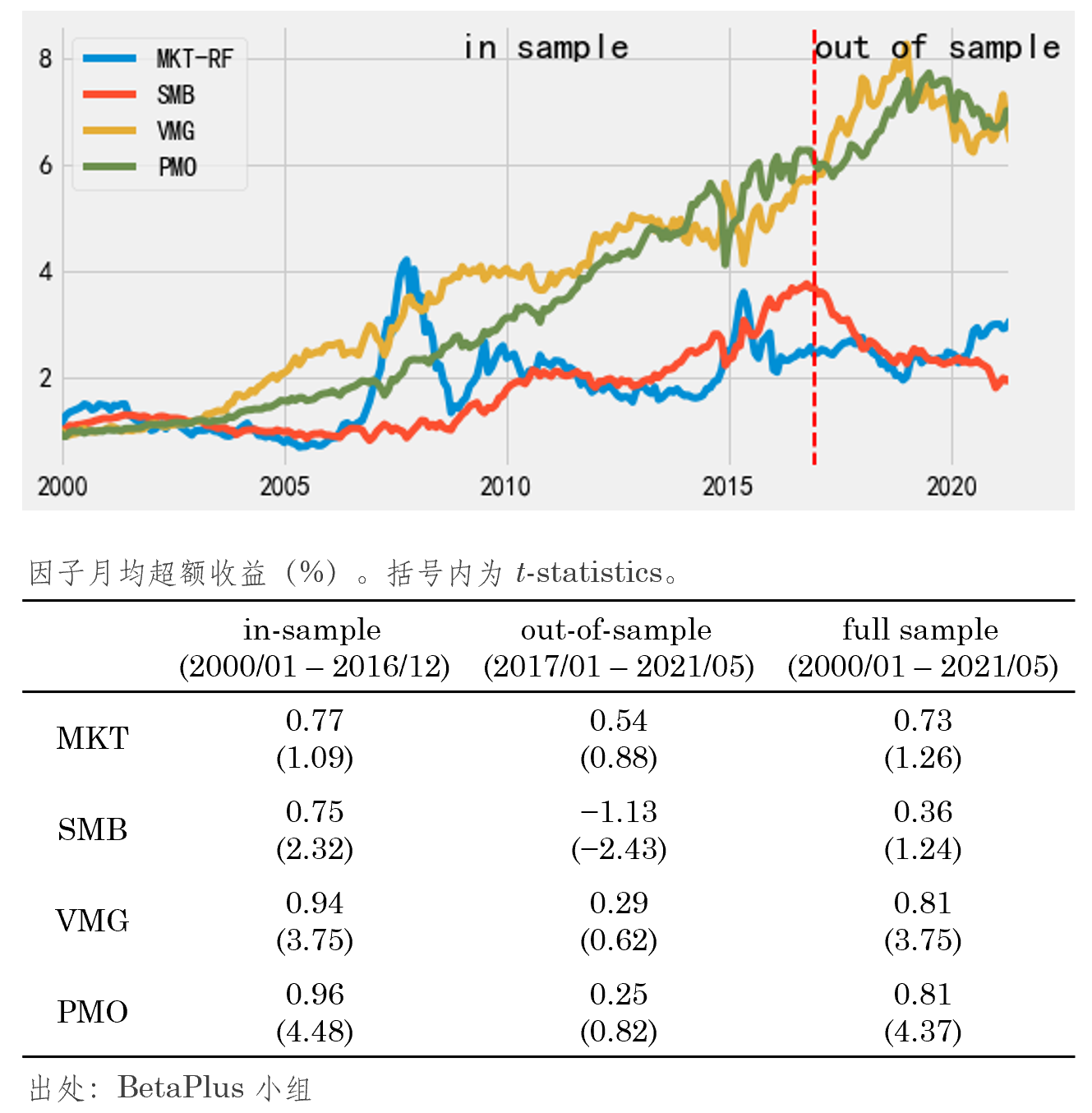
怎麽說呢(ne)?“此時(shí)無聲勝有聲”。看完了(le)美(měi)股,再來(lái)看看 A 股上中國版四因子的(de)表現。下(xià)圖統計了(le)市場(chǎng)、SMB、VMG(基于 Earnings-to-Price ratio 構造的(de)價值因子)以及 PMO 四因子在樣本内、外以及全樣本的(de)表現(樣本的(de)劃分(fēn)是根據該模型的(de)論文)。
Again,“此時(shí)無聲勝有聲”。此處無意進一步探討(tǎo)因子的(de)表現,隻是想通(tōng)過這(zhè)兩個(gè)例子引出本文要探討(tǎo)的(de)内容。在過去的(de) 30 年,學術界提出了(le)大(dà)量樣本内顯著的(de)因子和(hé)異象(zoo of factors),然而絕大(dà)多(duō)數在樣本外都無法持續。至于這(zhè)背後的(de)原因,目前有兩種主流看法。一種是由于多(duō)重假設檢驗,大(dà)多(duō)數因子都是 p-hacking 的(de)結果(Harvey, Liu, and Zhu (2016));另一種則是因子在樣本外之所以變差是因爲套利者把它們交易了(le)(McLean and Pontiff (2016))。
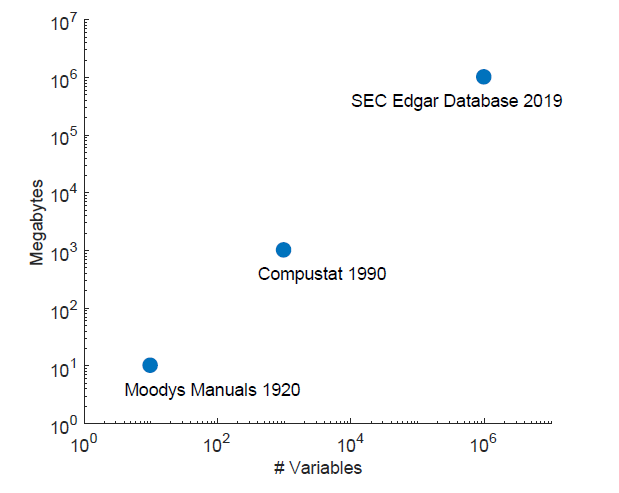
而今天要解讀的(de) Martin and Nagel (2019) 則給出了(le)第三種可(kě)能。該文題目是 Market Efficiency in the Age of Big Data,作者是 Ian Martin 和(hé) Stefan Nagel。看過上期推文的(de)小夥伴會知道這(zhè)就是我說的(de) Stefan Nagel 的(de)背靠背的(de)第二篇。針對(duì)大(dà)量樣本内顯著樣本外消失的(de)可(kě)預測性,該文提出了(le)一個(gè)新穎的(de)視角 —— high-dimensional investor learning。正如下(xià)圖所描繪的(de),在大(dà)數據時(shí)代,人(rén)們面對(duì)著(zhe)指數級增長(cháng)的(de)數據量,而能夠影(yǐng)響公司未來(lái)基本面的(de)變量也(yě)在無限擴張(例如會計報表數據,公司财報中的(de)措辭,分(fēn)析師一緻預期,量價數據,公司所處行業的(de)景氣度,以及各種宏觀經濟變量和(hé)其他(tā)另類數據)。在這(zhè)個(gè)背景下(xià),傳統的(de)實證資産定價檢驗受到了(le)巨大(dà)的(de)挑戰。
傳統實證資産定價假設理(lǐ)性預期(rational expectation),即假設投資者知道哪些變量影(yǐng)響公司基本面以及它們和(hé)基本面的(de)關系,即 基本面 = f(預測變量) 對(duì)投資者是已知的(de),并在這(zhè)個(gè)前提下(xià)通(tōng)過曆史數據(在樣本内)檢驗市場(chǎng)有效性。一旦原假設被拒絕便認爲變量獲得(de)的(de)超額收益代表著(zhe)風險補償或定價錯誤。然而,Martin and Nagel (2019) 指出,在大(dà)數據時(shí)代,投資者根本無法知道到底哪些變量能夠影(yǐng)響公司基本面,以及變量和(hé)基本面之間的(de)關系
從直觀上來(lái)理(lǐ)解,這(zhè)是因爲投資者高(gāo)維學習(xí)問題會導緻均衡狀态下(xià)資産的(de)價格和(hé)理(lǐ)性預期情況下(xià)相比出現偏差;該偏差的(de)存在将造成事後(ex post)從計量經濟學家的(de)視角來(lái)看,已實現收益率不再随機,而是包含了(le)一部分(fēn)可(kě)預測的(de)成分(fēn);因此當人(rén)們事後用(yòng)統計檢驗分(fēn)析變量和(hé)收益率的(de)關系時(shí),會誤以爲某些變量對(duì)收益率有預測性(且在高(gāo)維問題下(xià),即變量越來(lái)越多(duō)時(shí),這(zhè)個(gè)偏差造成的(de)影(yǐng)響愈加明(míng)顯)。
但實際的(de)情況是,對(duì)投資者來(lái)說,這(zhè)種可(kě)預測性在事前(ex ante)是感知不到的(de);對(duì)進行事後檢驗的(de)計量經濟學家來(lái)說,樣本内的(de)可(kě)預測性僅僅是源自由投資者學習(xí)
下(xià)面就來(lái)深度解讀這(zhè)篇文章(zhāng)。
2 Model
本節介紹 Martin and Nagel (2019) 使用(yòng)的(de)模型。令
由上式可(kě)知,模型中假設
其中
接下(xià)來(lái)是關于投資者的(de)設定。該文假設投資者是風險中性(risk-neutral)以及同質的(de)(homogeneous)。此外,他(tā)們還(hái)假設無風險收益率爲 0。在風險中性 + 無風險收益率爲 0 下(xià),資産的(de) risk premium 爲零,因此稍後對(duì)模型求解時(shí)發現的(de)任何 in-sample return predictability 都不應歸結爲 risk premium(因爲 risk premium 已經在模型中被排除了(le))。同質性則意味著(zhe)所有投資者對(duì)于
有了(le)資産和(hé)投資者,接下(xià)來(lái)就要開始研究投資者如何對(duì)資産估值、确定其均衡狀态下(xià)的(de)價格,以及在這(zhè)個(gè)過程中造成的(de)資産收益率的(de)可(kě)預測性。爲了(le)簡化(huà),Martin and Nagel (2019) 使用(yòng)了(le)單期估值模型。由于投資者是風險中性且利率爲零,因此
由上式可(kě)知,均衡狀态下(xià)資産的(de)價格
3 Rational Expectation
在探討(tǎo) investor learning 之前,我們先來(lái)看基準,即理(lǐ)性預期的(de)情況。理(lǐ)性預期下(xià)假設投資者知道真實的(de)
在理(lǐ)性預期下(xià),由于投資者無需估計
由于
從實證資産定價檢驗的(de)角度來(lái)說,我們關注的(de)是事後聯合檢驗
由
在沒有任何可(kě)預測性的(de)原假設下(xià),該投資組合在樣本内的(de)預期收益爲
4 OLS Learning
首先來(lái)看最簡單(但稍微不太滿足實際)的(de)情況 —— 投資者直接使用(yòng) OLS 來(lái)估計
然後用(yòng)
和(hé)理(lǐ)性預期(上一節)不同,由于投資者不知道真實的(de)
而 realized return 爲:
站在投資者在
将其代入
怎麽樣,在 OLS learning 下(xià),
和(hé)理(lǐ)性預期相比,投資者對(duì)
與理(lǐ)性預期相比,OLS learning 造成事後檢驗的(de)回歸系數
沒有可(kě)預測性的(de)原假設下(xià),
讓我們串一下(xià)上面“可(kě)預測性”産生的(de)邏輯。該邏輯是因爲投資者不知道
5 Bayesian Learning
通(tōng)過上一節的(de)介紹,希望各位小夥伴搞清楚 Martin and Nagel (2019) 想要幹什(shén)麽了(le)。但是我負責的(de)說,OLS learning 因爲有些問題,并不是他(tā)們關注的(de)重點。下(xià)面就來(lái)上點“硬貨”—— Bayesian learning。好消息是,有了(le) OLS learning 做(zuò)鋪墊,本節的(de)内容會容易理(lǐ)解地多(duō)(我寫起來(lái)也(yě)容易的(de)多(duō))。
爲了(le)簡化(huà)模型,Martin and Nagel (2019) 假設投資者的(de)先驗是
和(hé) OLS learning 相比,Bayesian learning 下(xià)的(de)
其中
1.
2.
3.
比較 Bayesian learning 和(hé) OLS learning 可(kě)知二者的(de)差異就體現在
在 Bayesian learning 下(xià),投資者通(tōng)過
毫無疑問,和(hé)理(lǐ)性預期以及 OLS learning 相比,這(zhè)個(gè)
上表中,我特地使用(yòng)了(le)相同的(de)顔色圈出了(le)相似的(de)項。和(hé) OLS learning 相比,Bayesian learning 中又多(duō)了(le)額外的(de)一項(第一項),而它的(de)第二項則對(duì)應 OLS learning 的(de)第一項,其中的(de)差異是,Bayesian Learning 的(de)第二項中多(duō)了(le)收縮系數
1. 第一項是因爲往先驗收縮,因此投資者對(duì)基本面信息
2. 第二項和(hé) OLS learning 類似,是噪聲對(duì)投資者估計的(de)影(yǐng)響。不過
3. 最後一項和(hé)理(lǐ)性預期一樣,爲
接下(xià)來(lái)如法炮制,利用(yòng)上述
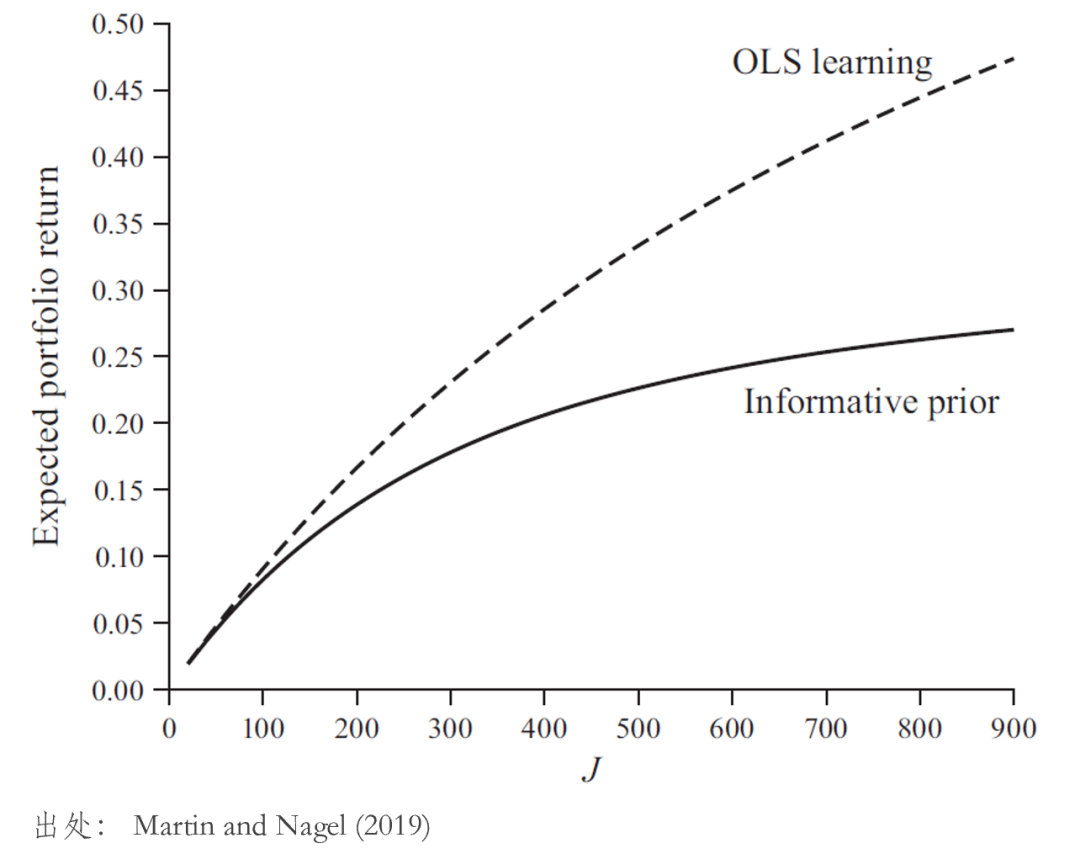
當
最後,我們再來(lái)回顧下(xià)“可(kě)預測性”産生的(de)原因。投資者通(tōng)過 Bayesian learning 估計
6 Out-of-Sample
以上就是關于投資者的(de) high-dimensional learning 如何影(yǐng)響事後樣本内統計檢驗的(de)研究。在該文的(de)後半部分(fēn),Martin and Nagel (2019) 也(yě)詳細討(tǎo)論了(le)樣本外的(de)可(kě)預測性。結論就是,investor learning 不會産生樣本外的(de)可(kě)預測性,這(zhè)顯然非常符合邏輯。按照(zhào)投資組合的(de)視角,它可(kě)以表述爲:
假設有兩個(gè)互不重疊的(de)時(shí)間窗(chuāng)口。如果我們使用(yòng)窗(chuāng)口 1 來(lái)檢驗
就我個(gè)人(rén)的(de)看法,Martin and Nagel (2019) 的(de)發現對(duì)學術界的(de)意義重大(dà)。在實證資産定價研究中,學術界通(tōng)常假設理(lǐ)性預期(即投資者不存在學習(xí)問題),因而無一例外都是事後通(tōng)過樣本内的(de)數據來(lái)檢驗某個(gè)異象或者因子的(de)超額收益是否顯著大(dà)于零。這(zhè)一慣例在過去 30 年内産生了(le)大(dà)量樣本内顯著的(de)異象,但是其中的(de)絕大(dà)多(duō)數在樣本外壓根不好使或者無法被複現(Hou, Xue, and Zhang (2020))。而究其原因,除了(le) p-hacking 以及被套利走之外,Martin and Nagel (2019) 給出了(le)另一個(gè)解釋。
在大(dà)數據時(shí)代,我們有了(le)過去無可(kě)比拟的(de)數據量。然而,投資者面臨更加複雜(zá)的(de)高(gāo)維預測和(hé)估計問題。大(dà)數據如何影(yǐng)響投資者的(de)估計,如何影(yǐng)響均衡狀态下(xià)資産的(de)價格,如何影(yǐng)響市場(chǎng)的(de)有效性?這(zhè)些都是等待回答(dá)的(de)問題。毫無疑問,Martin and Nagel (2019) 是一個(gè)有益和(hé)大(dà)膽的(de)嘗試,而它提出的(de) investor learning 問題也(yě)足以引起人(rén)們的(de)重視。
所有曆史數據都是樣本内[3]。
備注:
[1] 但這(zhè)絲毫不影(yǐng)響這(zhè)是一個(gè)很好的(de)開端,我們也(yě)有理(lǐ)由期待今後拓展的(de)模型會有更深入的(de)發現。
[2] 如果
[3] 見《所有曆史數據都是樣本内》。
參考文獻
Carhart, M. M. (1997). On persistence in mutual fund performance. Journal of Finance 52(1), 57 – 82.
Fama, E. F. and K. R. French (2015). A five-factor asset pricing model.Journal of Financial Economics 116(1), 1 – 22.
Harvey, C. R., Y. Liu, and H. Zhu (2016). … and the cross-section of expected returns. Review of Financial Studies 29(1), 5 – 68.
Hou, K., C. Xue, and L. Zhang (2020). Replicating anomalies. Review of Financial Studies 33(5), 2019 – 2133.
McLean, R. D. and J. Pontiff (2016). Does academic research destroy stock return predictability? Journal of Finance 71(1), 5 – 32.
Martin, I. and S. Nagel (2019). Market efficiency in the age of big data. Working paper, available at: https://ssrn.com/abstract=3511296.
免責聲明(míng):入市有風險,投資需謹慎。在任何情況下(xià),本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià),本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外,文中圖表均直接或間接來(lái)自于相應論文,僅爲介紹之用(yòng),版權歸原作者和(hé)期刊所有。