出色不如走運 (VI) ?

發布時(shí)間：2021-07-04 | 來(lái)源: 川總寫量化(huà)

作者：石川

摘要：本文帶你了(le)解學術界關于 p-hacking 問題是否嚴重的(de)最新思辨。

1 p-hacking

沒想到這(zhè)麽快(kuài)就續上了(le)《出色不如走運》系列[1]。自 2016 年以來(lái)，以 Cam Harvey 和(hé) Yan Liu 爲代表的(de)一批學者開始呼籲應在金融研究中重視 p-hacking 問題帶來(lái)的(de)僞發現（見 Harvey (2017), Harvey, Liu, and Zhu (2016), Harvey and Liu (2020, 2021a) 以及 Chordia, Goyal, and Saretto (2020) 等）。這(zhè)些文章(zhāng)的(de)觀點是，由于 p-hacking 問題，很多(duō)樣本内顯著的(de)異象（或因子，本文統稱爲異象）都是虛假的(de)。

此外，Hou, Xue, and Zhang (2020) 複現了(le) 452 個(gè)異象，發現 65% 的(de)異象的(de) t-statistics 在 2.0 以下(xià)，并不顯著；而如果考慮多(duō)重假設檢驗問題，該比例甚至上升至 82%。該實證結果支持了(le)大(dà)部分(fēn)異象是虛假的(de)這(zhè)一觀點。

然而，當學術界逐漸接受并重視這(zhè)個(gè)問題的(de)時(shí)候（例如 Journal of Finance 以及 Review of Financial Studies 都有各自的(de) code-sharing policy），在最近一年有一些最新的(de)文章(zhāng)卻提出了(le)不同的(de)看法，認爲發表的(de)諸多(duō)異象有足夠的(de)可(kě)信度。這(zhè)其中的(de)代表要數來(lái)自 AQR 的(de)這(zhè)篇 Jensen, Kelly, and Pedersen (2021)。該文一頓操作猛如虎之後，提出了(le)和(hé) Hou, Xue, and Zhang (2020) 完全不同的(de)觀點，認爲有将近 85% 的(de)異象可(kě)以被複現，從而說明(míng)學術發表很靠譜。但是仔細閱讀可(kě)知，雖然 Jensen, Kelly, and Pedersen (2021) 提出了(le) empirical Bayesian 方法來(lái)檢驗異象，但其可(kě)複現比例的(de)巨大(dà)提升卻來(lái)自于該文使用(yòng)了(le)和(hé) Hou, Xue, and Zhang (2020) 不同的(de)數據和(hé)方法來(lái)構造異象，這(zhè)個(gè)操作幾乎就把可(kě)複現的(de)比例翻了(le)一倍（但這(zhè)難道不是一種 p-hacking？）。

除了(le) AQR 的(de)這(zhè)篇文章(zhāng)之外，Chen and Zimmermann (2020) 也(yě)提出了(le)類似的(de)看法，認爲大(dà)部分(fēn)異象的(de)樣本内檢驗結果是可(kě)信的(de)。該文研究了(le)異象在樣本外預期收益相對(duì)樣本内的(de)收縮系數（shrinkage factor）。一般來(lái)說，如果這(zhè)個(gè)系數很高(gāo)，那就說明(míng)樣本内過拟合的(de)問題更嚴重。但 Chen and Zimmermann (2020) 的(de)研究表明(míng)，這(zhè)個(gè)收縮系數僅爲 12%。這(zhè)意味著(zhe)，如果一個(gè)異象樣本内年化(huà)收益是 10%，那麽它樣本外的(de)年化(huà)收益是 $10\%\times(1-0.12)=8.8\%$ 。

另外值得(de)一提的(de)是，Chen and Zimmermann (2020) 認爲該文的(de)一大(dà)亮點是和(hé)像 McLean and Pontiff (2016) 使用(yòng)真正樣本外研究不同，他(tā)們僅僅使用(yòng)了(le)樣本内的(de)數據進行的(de)分(fēn)析并得(de)出了(le)上述結論：Our adjustment uses only in-sample data and provides sharper inferences than out-of-sample tests. 看到這(zhè)個(gè)，我不禁想起了(le)上期推文剛剛介紹的(de) Martin and Nagel (2019) 所提出的(de) high-dimensional investor learning 問題造成的(de)樣本内虛假的(de)顯著性，所以就隻能呵呵了(le)。

如果以上對(duì)部分(fēn)文獻的(de)梳理(lǐ)足以引起了(le)你的(de)興趣，那麽接下(xià)來(lái)我們就要上“正餐”了(le)。本文真正要介紹的(de)是 Chen (2021) 和(hé) Harvey and Liu (2021b)。Chen (2021) 通(tōng)過 thought experiments 指出 p-hacking alone 根本無法解釋學術界發現的(de)諸多(duō)非常顯著的(de)異象（例如那些 t-statistics 超過 6.0 或者 8.0 的(de)），并通(tōng)過他(tā)的(de)模型得(de)出了(le)一系列令人(rén)震驚的(de)推論（先賣個(gè)關子，本文第二節再討(tǎo)論），間接指出對(duì)于 p-hacking 的(de)擔憂可(kě)能被 Cam Harvey 和(hé) Yan Liu 誇大(dà)了(le)。Harvey and Liu (2021b) 則對(duì) Chen (2021) 的(de)諸多(duō)推論以及 Chen and Zimmermann (2020) 所提出的(de) 12% 的(de)收縮系數逐一進行了(le)回應。

在介紹這(zhè)兩篇文章(zhāng)之前，我們不妨先來(lái)思考一下(xià)，當人(rén)們談及 p-hacking 的(de)時(shí)候，到底關心的(de)是什(shén)麽。無論是學術界還(hái)是業界，大(dà)家共同的(de)認知是所有異象預期收益聯合爲零這(zhè)個(gè)原假設一定會被拒絕，即人(rén)們都認可(kě)有一部分(fēn)異象是顯著的(de)。因此，研究 p-hacking 時(shí)，從來(lái)就不擔心僅靠 p-hacking 無法解釋特别顯著的(de)真實的(de)異象。事實上，Cam Harvey 和(hé) Yan Liu 的(de)一系列文章(zhāng)也(yě)從沒表示出類似的(de)觀點，而是關注于以下(xià)這(zhè)兩個(gè)真正需要被回答(dá)的(de)問題：

1. 在 p-hacking 以及 publication bias 的(de)影(yǐng)響下(xià)，有多(duō)少比例的(de)異象是真實的(de)？人(rén)們認同 p-hacking alone 無法解釋 t-statistics 超過 6.0 或者 8.0 的(de)異象，但也(yě)知道它會造成很多(duō) t-statistics 爲 2.0 或者 3.0 的(de)異象。而所有異象中，到底有多(duō)少是真實的(de)？

2. 對(duì)于通(tōng)過檢驗的(de)異象（即被認爲是真實的(de)），它們樣本外收益率的(de)收縮系數是多(duō)少？

這(zhè)兩個(gè)問題才是研究 p-hacking 時(shí)應該回答(dá)的(de)問題。當然，回答(dá)這(zhè)些問題并不容易，而基于不同的(de)假設可(kě)能會得(de)到千差萬别的(de)結論。以下(xià)兩節就來(lái)分(fēn)别解讀 Chen (2021) 和(hé) Harvey and Liu (2021b)，并把判斷留給各位小夥伴。本文最後一節會給出思考。

2 質疑

Chen (2021) 是 Journal of Finance forthcoming.

該文的(de)推論是基于一個(gè)假設和(hé)一個(gè)核心公式。它的(de)假設是所有異象的(de) t-statistics 都滿足标準正态分(fēn)布，即所有異象的(de)原假設都是預期收益爲零。BTW，這(zhè)個(gè)假設按照(zhào)學術界的(de)術語被稱作 ensemble null。此外，對(duì)于每個(gè)異象，取決于其 t-statistic 的(de)高(gāo)低，它都有一定的(de)概率被觀測到（即被發表出來(lái)）。隻不過這(zhè)個(gè)概率分(fēn)布在 Chen (2021) 中是抽象的(de)，該文的(de)結論不依賴于具體的(de)分(fēn)布。

在上述設定下(xià)，Chen (2021) 的(de)核心公式如下(xià)：

$\displaystyle\mbox{E}[N]\ge\frac{\mbox{E}[\mbox{num observed }(|t_i|>\bar t)]}{\mbox{prob}(|Z|>\bar t)}$

式中 $N$ 是嘗試的(de)異象的(de)個(gè)數（強調：包括發表的(de)和(hé)沒有發表的(de)）， $Z$ 是标準正态分(fēn)布随機變量， $\bar t$ 是給定的(de) t-statistic 阈值。該式的(de)含義是爲了(le)觀測到 $\mbox{E}[\mbox{num observed }(|t_i|>\bar t)]$ 個(gè) t-statistic 絕對(duì)值不低于 $\bar t$ 的(de)異象，所需要嘗試的(de)異象的(de)個(gè)數的(de)下(xià)限。利用(yòng)這(zhè)個(gè)式子和(hé)實際異象的(de)數據，Chen (2021) 得(de)到了(le)一系列推論。下(xià)表就是該文最重要的(de)結果。

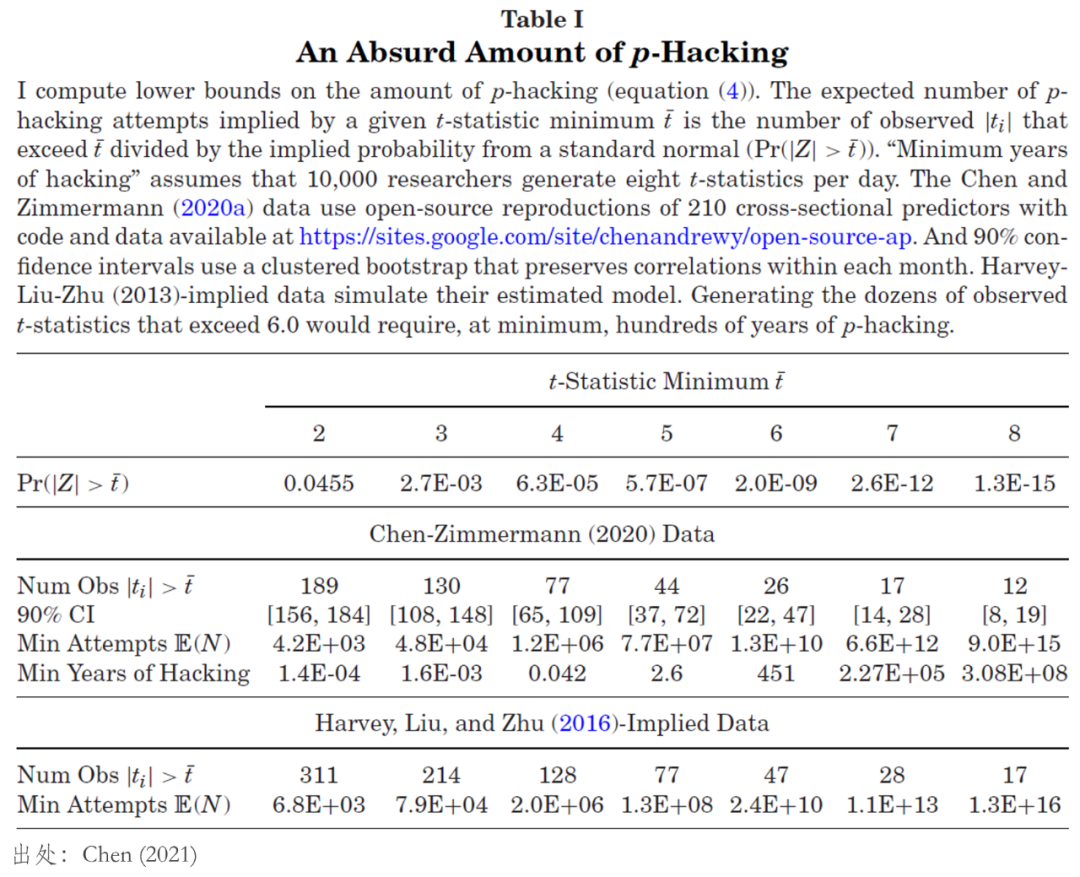
首先，該表的(de)最上面部分(fēn)給出了(le)标準正态分(fēn)布下(xià) $|Z|$ 大(dà)于不同 $\bar t$ 取值的(de)概率。中間部分(fēn)和(hé)最下(xià)面部分(fēn)分(fēn)别使用(yòng)了(le)兩組不同的(de)異象數據，統計了(le)其中超過各 $\bar t$ 的(de)異象的(de)個(gè)數，然後就利用(yòng)前述核心公式計算(suàn)了(le) $\mbox{E}[N]$ 的(de)下(xià)限。以他(tā)們自己的(de)異象數據爲例，在 210 個(gè)異象中 t-statistics 超過 6.0 的(de)共有 26 個(gè)，結合 $\mbox{prob}(|Z|>\bar t)=2.0\times 10^{-9}$ ，能夠推出 $\mbox{E}[N]$ 的(de)下(xià)限爲 $1.3\times 10^{10}$ 。該數值的(de)中文含義是，爲了(le)找到 26 個(gè) t-statistics 超過 6.0 的(de)異象，學術界至少要嘗試 130 億個(gè)異象。如果傾全美(měi)所有經濟學教授和(hé)經濟學家之力，大(dà)家不吃(chī)不喝每天挖異象，那麽要挖 451 年。顯然，這(zhè)是不可(kě)能的(de)，因此 Chen (2021) 指出僅靠 p-hacking 自身是無法造成這(zhè)麽顯著的(de)結果的(de)。另外，從上表中還(hái)可(kě)以推斷出，未發表和(hé)發表的(de)異象個(gè)數之比高(gāo)達 $10^{14}:1$ 。最後，該文還(hái)研究了(le)不同 t-statistics 異象的(de)發表概率。在該模型下(xià)，t-statistic = 8.0 的(de)異象被發表的(de)概率是 t-statistic = 2.5 的(de)異象被發表的(de)概率的(de) $10^{10}$ 倍。下(xià)表彙總了(le) Chen (2021) 的(de)三點推論（第三節中将會和(hé) Harvey and Liu (2021a) 做(zuò)對(duì)比）。

毫無疑問，模型給出的(de)這(zhè)些數據足夠令人(rén)震驚，也(yě)完全不符合認知。正因如此，Chen (2021) 總結到，靠 p-hacking 本身，學術界是不可(kě)能發表出這(zhè)麽多(duō)特别顯著的(de)異象的(de)，異象背後一定有風險補償或錯誤定價等合理(lǐ)的(de)原因。

Well, true!

上述觀點确實沒有問題，相信你我都會同意。但再仔細思考一下(xià)，兩個(gè)問題也(yě)同時(shí)浮出水(shuǐ)面：（1）在 Chen (2021) 利用(yòng) ensemble null 假設得(de)出了(le)一些匪夷所思的(de)推論，這(zhè)是否恰恰意味著(zhe)這(zhè)個(gè)假設本身就有待商榷？（2）誰也(yě)沒說僅靠 p-hacking 本身就能産生所有顯著的(de)異象，而正如本文第一節強調的(de)，我們關心的(de)是 p-hacking 造成了(le)多(duō)大(dà)比例的(de)虛假異象，以及對(duì)真實異象，它們樣本外的(de)預期收益應該打多(duō)少折扣（shrinkage factor）？

對(duì)于（1），問題的(de)核心在于在标準正态分(fēn)布下(xià)，特别高(gāo)的(de) $\bar t$ 發生的(de)概率微乎其微。當它作爲分(fēn)母時(shí)，計算(suàn)出的(de) $\mbox{E}[N]$ 自然也(yě)就是天文數字。但是 ensemble null 這(zhè)個(gè)假設合理(lǐ)嗎？如果它被其他(tā)更合理(lǐ)的(de)假設所取代，那麽上述三個(gè)定量的(de)推論是否會發生變化(huà)呢(ne)？對(duì)于（2），Chen (2021) 的(de) thought experiments 僅僅是傳遞出僅靠 p-hacking 無法産生大(dà)量 t-statistics 非常高(gāo)的(de)異象（but we all knew it！），而沒有正面回答(dá)那兩個(gè)真正需要回答(dá)的(de)問題。（所以，這(zhè)篇文章(zhāng) Journal of Finance forthcoming 還(hái)挺讓我意外的(de)。）

3 回應

再來(lái)看看 Harvey and Liu (2021b) 對(duì) Chen (2021) 的(de)回應。Harvey and Liu (2021b) 和(hé) Chen (2021) 的(de)兩點區(qū)别是：（1）該文沒有使用(yòng) ensemble null 假設，而是借鑒基金研究使用(yòng)了(le)一個(gè)更合理(lǐ)的(de)假設，在這(zhè)個(gè)假設下(xià)該文得(de)到了(le)和(hé) Chen (2021) 完全不同的(de)推論；（2）該文回答(dá)了(le)第一節提到的(de)關于 p-hacking 的(de)兩個(gè)核心問題。

在基金研究中，比起 ensemble null，另一種常見假設是 bi-modal mean 分(fēn)布（Barras, Scaillet, and Wermers (2010), Harvey and Liu (2018)），即假設所有基金的(de)超額收益來(lái)自兩個(gè)分(fēn)布：其中絕大(dà)部分(fēn)來(lái)自均值爲零的(de)分(fēn)布，而一小撮來(lái)自均值大(dà)于零的(de)分(fēn)布。放到異象上，這(zhè)對(duì)應的(de)就是假設絕大(dà)部分(fēn)異象是虛假的(de)，因此它們預期收益來(lái)自均值爲零的(de)分(fēn)布，而一小撮異象是真實的(de)，它們的(de)預期收益來(lái)自均值非零的(de)分(fēn)布。

The bi-modal mean (alpha) distribution generates a mixture distribution for t-statistics, where low t-statistics are likely drawn from the zero-mean distribution and very large t-statistics are almost surely drawn from the non-zero mean distribution.

雖然研究異象能夠借鑒基金研究的(de)分(fēn)布，但這(zhè)二者之間還(hái)有另一個(gè)巨大(dà)的(de)差異。對(duì)基金的(de)超額收益進行檢驗和(hé)推斷時(shí)，不存在觀測不到的(de)基金造成的(de)影(yǐng)響；但對(duì)異象的(de)超額收益檢驗和(hé)推斷時(shí)，除去被發表的(de)異象，還(hái)需要考慮因爲不夠顯著而被學者們放棄的(de)異象以及雖然顯著但因爲 publication bias 而未能發表的(de)異象。這(zhè)二者和(hé)被發表的(de)異象一起，構成了(le)總共被嘗試的(de)異象。

Harvey and Liu (2021b) 在模型中使用(yòng)參數 $N_0$ 來(lái)表示總共被嘗試的(de)異象的(de)個(gè)數。由于他(tā)們使用(yòng)了(le) bi-modal mean 分(fēn)布，因此假設 $p_0$ 比例的(de)異象的(de)預期收益大(dà)于零。有小夥伴會問，對(duì)于這(zhè)部分(fēn)異象，如何确定其分(fēn)布的(de)參數？對(duì)此，Harvey and Liu (2021b) 使用(yòng)了(le) bootstrap 方法[2]。另一方面，爲了(le)直接對(duì)發表過程建模，他(tā)們假設異象發表的(de)概率爲：

$\displaystyle\mbox{prob}(\mbox{$t$-stat})=\frac{\gamma_1}{2\gamma_1+\exp(-\gamma_2(\mbox{$t$-stat}-2.0))}$

其中 $\gamma_1$ 和(hé) $\gamma_2$ 爲大(dà)于零的(de)常數。這(zhè)個(gè)函數滿足随異象的(de) t-statistic 單調遞增，且當 t-statistic 趨于無窮大(dà)時(shí)，該概率趨于 0.5。這(zhè)可(kě)以被認爲是個(gè)合理(lǐ)的(de)假設，因爲哪怕是再高(gāo)的(de) t-statistic 也(yě)無法保證異象能夠被發表（比如異象沒有任何 economic sense）。以上 $[N_0,p_0,\gamma_1,\gamma_2]$ 就構成了(le) Harvey and Liu (2021b) 模型中的(de)全部參數。和(hé) Chen (2021) 相比，該模型有以下(xià)幾點不同（優勢）：

1. 通(tōng)過 $N_0$ 考慮了(le)所有被嘗試過的(de)異象，而非僅僅關注于被發表的(de)異象（Chen (2021) 的(de) thought experiments 是基于被發表的(de)異象）；

2. 通(tōng)過 $p_0$ （和(hé) bootstrap），使用(yòng) bi-modal mean 取代 ensemble null 假設，更符合人(rén)們對(duì)異象數據的(de)認知；

3. 利用(yòng) $\gamma_1$ 和(hé) $\gamma_2$ 定量描繪了(le)異象發表過程。

有了(le)模型，接下(xià)來(lái)就是通(tōng)過模型來(lái)模拟（simulation）異象被發表的(de)過程，并根據真實被發表的(de)異象的(de)數據來(lái)對(duì)模型的(de)參數 $[N_0,p_0,\gamma_1,\gamma_2]$ 進行校準（calibration）。先來(lái)說模拟。由于 $N_0$ 代表所有被嘗試的(de)異象（包括發表的(de)和(hé)沒有發表的(de)），因此需要一個(gè)巨大(dà)的(de)異象池并從中抽取 $N_0$ 個(gè)。爲此，Harvey and Liu (2021b) 同時(shí)使用(yòng)了(le) Chen and Zimmermann (2020) 中提及的(de) 156 個(gè)被發表的(de)異象和(hé) Yan and Zheng (2017) 通(tōng)過純 data-mining 生成的(de) 18,000+ 個(gè)異象作爲候選的(de)異象池。

模拟的(de)第一步是從上述合并異象池中生成 $N_0$ 個(gè)異象。值得(de)說明(míng)的(de)是，由于被發表的(de)異象一定是被試過的(de)，因此在每次模拟中，那 156 個(gè)被發表的(de)異象都會出現在 $N_0$ 個(gè)異象中；剩餘 $N_0-156$ 個(gè)異象則從 Yan and Zheng (2017) 的(de)池子中随機抽取。令 $D_{CZ}$ 表示 $T\times 156$ 階矩陣，儲存 156 個(gè)異象的(de) $T$ 期收益率序列； $D_{YZ}^n$ 表示 $T\times N_0-156$ 階矩陣，儲存剩餘異象的(de)收益率序列；最後 $D^n=[D_{CZ},D_{YZ}^n]$ 表示第 $n$ 次模拟中生成的(de) $N_0$ 個(gè)異象的(de)收益率序列矩陣。

模拟的(de)第二步是利用(yòng) bi-modal mean 模型計算(suàn)異象 t-statistics。首先，使用(yòng) $D^n$ 計算(suàn)全部異象的(de) t-statistics 絕對(duì)值，保留絕對(duì)值最高(gāo)的(de) $N_0\times p_0$ 個(gè)異象，并把剩餘 $N_0\times(1-p_0)$ 個(gè)異象的(de)收益率在時(shí)序上去均值。如此操作後得(de)到的(de) $T\times N_0$ 階收益率序列矩陣記爲 $\hat D^n$ 。然而，這(zhè)波操作僅僅保證了(le)原假設成立（ $p_0$ 的(de)異象爲真， $1-p_0$ 的(de)異象爲假）。由于樣本分(fēn)布和(hé)總體分(fēn)布會有差異，因此 Harvey and Liu (2021b) 對(duì)每一個(gè) $\hat D^n$ 又進行了(le)一層 bootstrap，以此來(lái)模拟實際的(de)收益率序列。對(duì) $\hat D^n$ 的(de)第 $m$ 次 bootstrap 得(de)到的(de)收益率序列記爲 $\hat D^{n_m}$ 。

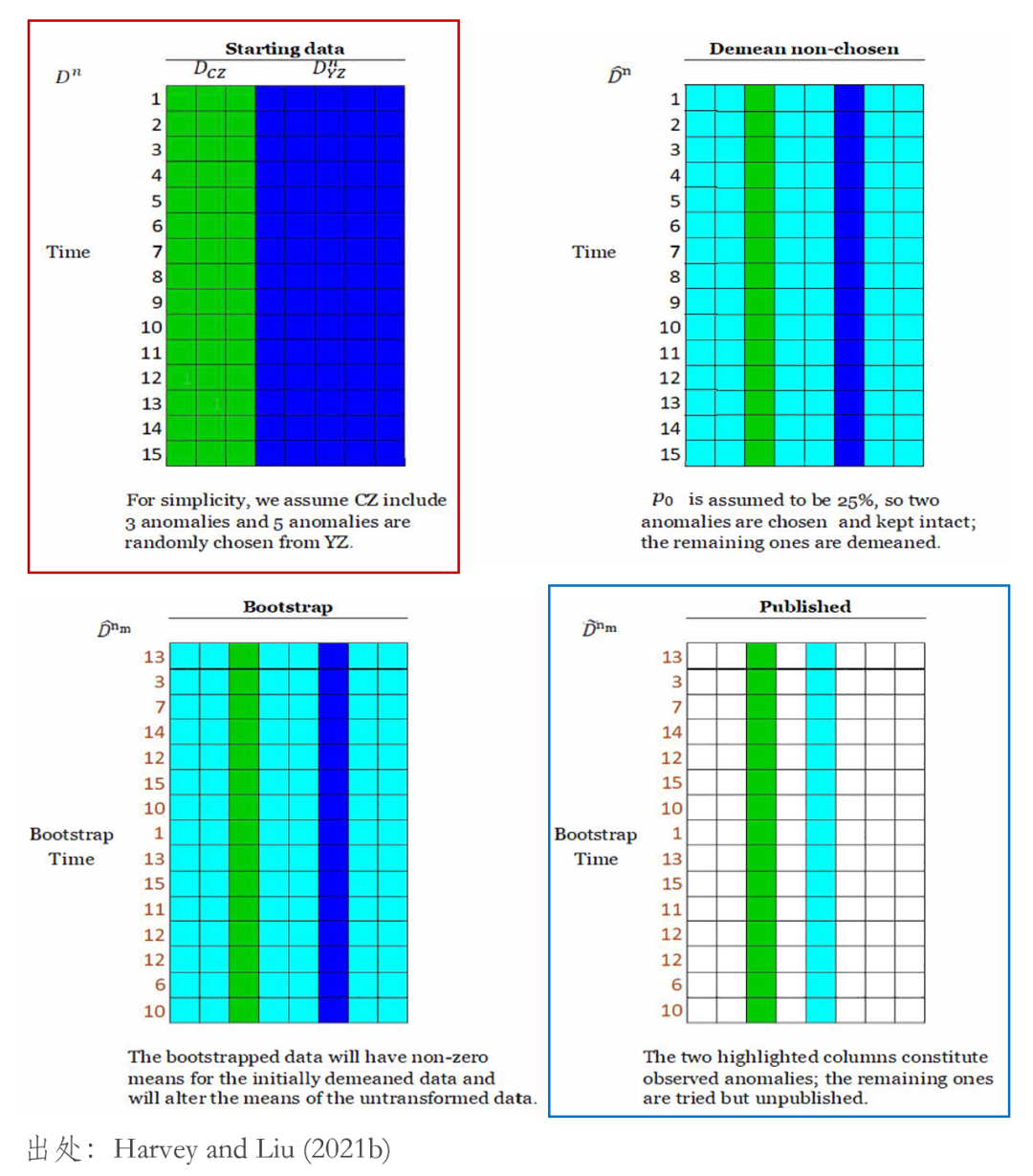
模拟的(de)第三步是确定哪些異象被發表。對(duì)于每個(gè) $\hat D^{n_m}$ ，計算(suàn)其中每個(gè)異象的(de) t-statistic 并使用(yòng) $\mbox{prob}(\mbox{$t$-stat})$ 的(de)公式計算(suàn)其被發表的(de)概率 $p_i$ 。對(duì)每個(gè)異象，随機生成一個(gè)在 0 和(hé) 1 之間均勻分(fēn)布的(de)變量，若它的(de)取值小于 $p_i$ 則認爲異象被發表，反之則沒有被發表。令 $\tilde N_{n_m}$ 代表矩陣 $\hat D^{n_m}$ 中最終被發表的(de)異象的(de)個(gè)數；令 $\tilde D^{n_m}$ 儲存所有被發表異象的(de)收益率序列。

OK！希望上面的(de)介紹足夠清楚了(le)……如果還(hái)沒有，下(xià)面通(tōng)過一個(gè)圖例來(lái)加深理(lǐ)解。圖中紅色框出來(lái)的(de)部分(fēn)代表了(le)模拟中的(de)第一步；藍色框出來(lái)的(de)部分(fēn)代表模拟的(de)第三步；次對(duì)角線上的(de)兩張圖代表了(le)模拟的(de)第二步。

爲了(le)便于理(lǐ)解，圖例中假設 $N_0=8$ ，且被發表的(de)異象是 3 個(gè)（綠色部分(fēn)是它們的(de)收益率時(shí)序）；此外，從 Yan and Zheng (2017) 中随機抽取了(le) 5 個(gè)（深藍色表示它們的(de)收益率時(shí)序），這(zhè)就構成了(le)第一步的(de) $D^n$ 。圖例第二步中假設 $p_0=25\%$ ，因此有 2 個(gè)異象是真的(de)。計算(suàn)這(zhè) 8 個(gè)異象的(de) t-statistics 并選擇絕對(duì)值最高(gāo)的(de)兩個(gè)（維持了(le)綠色和(hé)藍色，即假設一個(gè)來(lái)自發表的(de)異象，另一個(gè)來(lái)自 Yan and Zheng (2017)），把其餘異象收益率在時(shí)序上去均值（青色），得(de)到 $\hat D^n$ 。緊接著(zhe)對(duì)它進行下(xià)一層 bootstrap，得(de)到 bootstrapped 樣本 $\hat D^{n_m}$ 。觀察上圖中左下(xià)方的(de)那副圖可(kě)知，它的(de)時(shí)間戳已經是被打亂的(de)了(le)（代表 bootstrapped 樣本）。最後，在模拟的(de)第三步，根據發表概率确定哪些異象被發表。圖例中假設兩個(gè)真實的(de)異象被發表，其餘的(de)異象未被發表。

說完了(le)模拟，接下(xià)來(lái)就要說參數校準。對(duì)于任何一組給定的(de)參數 $[N_0,p_0,\gamma_1,\gamma_2]$ ，通(tōng)過上述雙層的(de) bootstrap，都可(kě)以模拟出一些被發表的(de)異象。然而，哪組參數才是正确的(de)呢(ne)？這(zhè)就要看在哪組參數下(xià)，模拟産生的(de)被發表的(de)異象的(de)某些統計指标更加符合實際被發表的(de)異象的(de)統計指标。爲此，Harvey and Liu (2021b) 選擇了(le)實際被發表異象的(de) t-statistics 的(de)五個(gè)分(fēn)位數（5th，10th，50th，90th，95th）以及顯著的(de)異象的(de)個(gè)數作爲校準的(de)統計指标。

需要說明(míng)的(de)是，在 156 個(gè)異象中，僅有 132 個(gè)異象的(de) t-statistics 高(gāo)于 2.0。因此，前述 t-statistics 的(de)五個(gè)分(fēn)位數是使用(yòng)者 132 個(gè)異象計算(suàn)的(de)，且顯著異象的(de)個(gè)數也(yě)是 132 而非 156。最終校準的(de)目标是選擇合适的(de)參數，使得(de)模拟生成的(de)指标和(hé)真實的(de)指标之間的(de)誤差平方的(de)加權平均最小：

$\displaystyle\mbox{obj func}=\frac{1}{MN}\sum_{n=1}^N\sum_{m=1}^M\left(\sum_{j=1}^5\tilde w_j\left(\tilde{pc}_j^{n_m}-pc_{0,j}\right)^2+\tilde w_N\left(\tilde N_{n_m}-132\right)^2\right)$

其中 $\tilde{pc}_j^{n_m}$ 表示利用(yòng) $\tilde D^{n_m}$ 中發表的(de)異象收益率序列計算(suàn)的(de) t-statistics 分(fēn)位數， $pc_{0,j}$ 表示利用(yòng) 132 個(gè)異象計算(suàn)的(de) t-statistics 分(fēn)位數； $\tilde N_{n_m}$ （前面介紹過）是 $\tilde D^{n_m}$ 中儲存的(de)發表的(de)異象的(de)個(gè)數，而 132 是真實的(de)被發表的(de)異象的(de)個(gè)數。

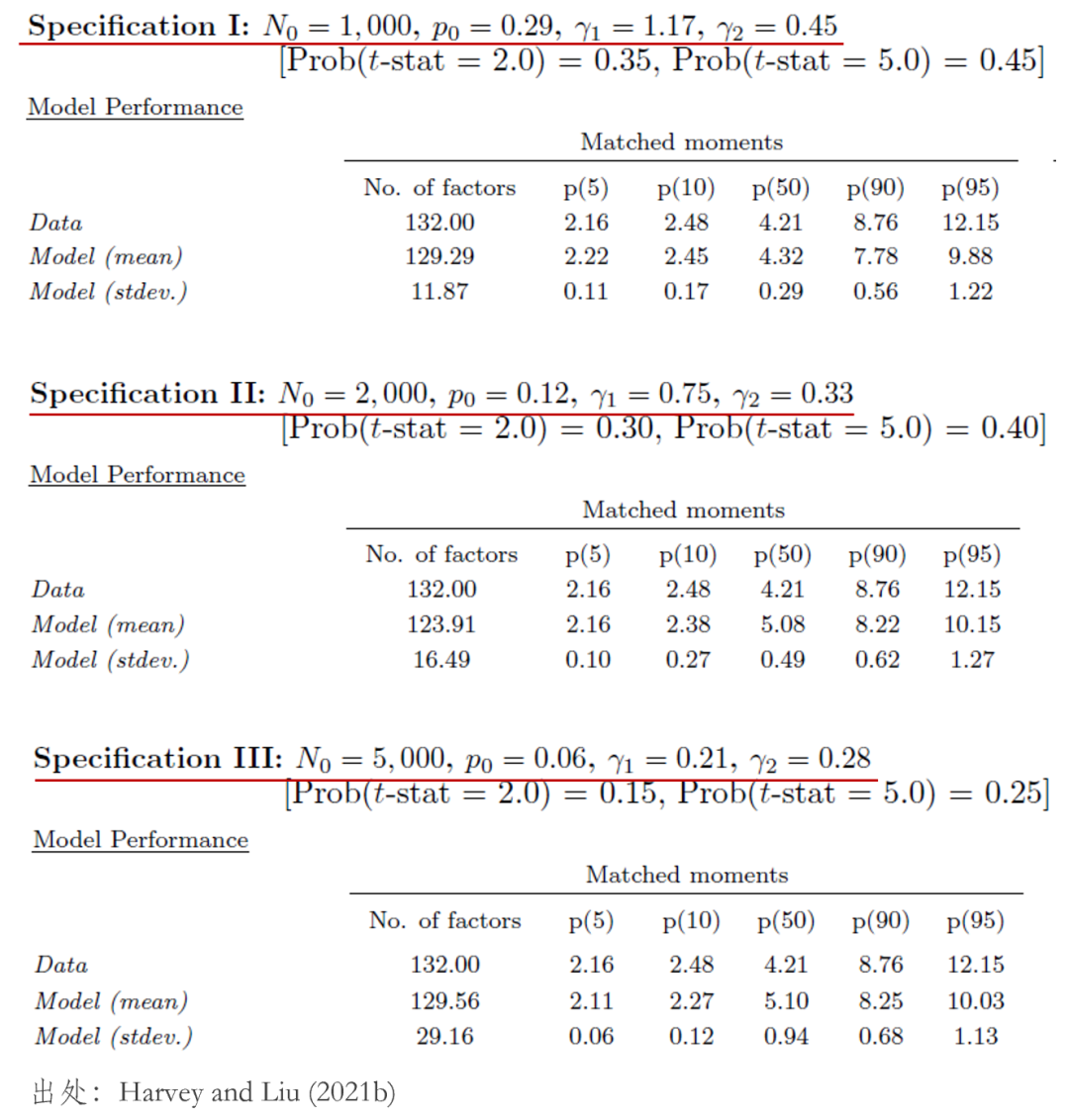
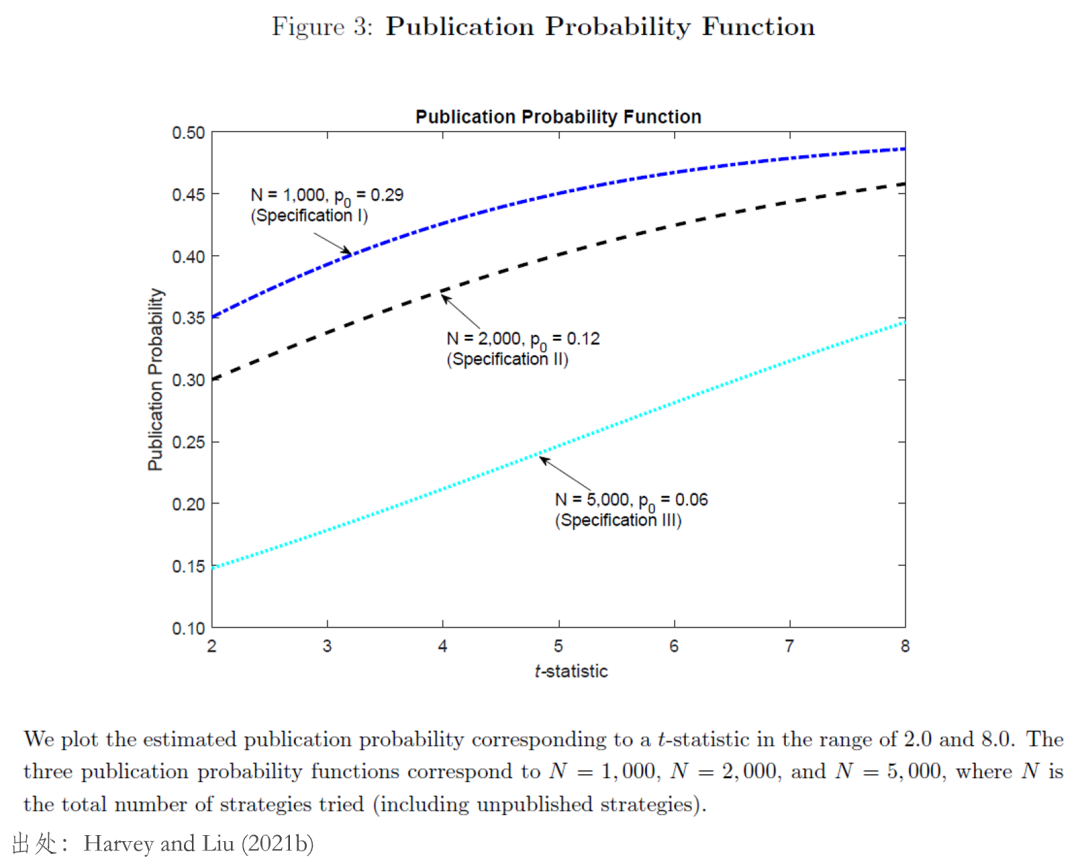
由前述對(duì)模拟的(de)說明(míng)，該模拟過程其實是雙層的(de) bootstrap：（1）第一層是生成不同的(de) $N_0$ 個(gè)異象的(de)樣本；（2）第二層是對(duì)于每組 $N_0$ （即 $D^n$ ），通(tōng)過 bootstrap 生成收益率序列并決定哪些被發表，即得(de)到 $\tilde D^{n_m}$ 。因此，對(duì)于任何一組給定的(de)參數 $[N_0,p_0,\gamma_1,\gamma_2]$ ，最終都有 $M\times N$ 個(gè)模拟，而目标函數是它們的(de)均值。此外，由于進行了(le)多(duō)次模拟，因此能夠方便的(de)計算(suàn)每個(gè)指标（上述 5 個(gè)分(fēn)位數以及發表的(de)異象的(de)個(gè)數）的(de)标準差。在目标函數中， $\tilde w_j$ 和(hé) $\tilde w_N$ 分(fēn)别等于标準差的(de)倒數，以此來(lái)決定不同指标在目标函數中的(de)權重。

有了(le)目标函數，Harvey and Liu (2021b) 給每個(gè)參數選了(le)範圍，然後進行了(le)大(dà)規模的(de) search。不過也(yě)許接下(xià)來(lái)的(de)結果讓你意想不到，那就是這(zhè)個(gè)問題本身是未識别的(de)（not identified），換句話(huà)說，它的(de)最優參數不唯一。該文正文部分(fēn)彙報的(de)三組參數 $[N_0,p_0,\gamma_1,\gamma_2]$ 如下(xià)圖所示。在這(zhè)三組參數下(xià)，模拟得(de)到的(de)五個(gè) t-statistics 分(fēn)位數和(hé)發表異象個(gè)數都和(hé)實際值較好地吻合。

可(kě)以看到，在這(zhè)三組參數中， $N_0$ 分(fēn)别等于 1000，2000 和(hé) 5000。而這(zhè)個(gè)問題之所以是未識别的(de)，原因恰恰是我們觀察到的(de)隻有被發表的(de)異象，而真正的(de) $N_0$ （學術界到底嘗試了(le)多(duō)少個(gè)異象）永遠(yuǎn)是未知的(de)。這(zhè)是在研究 p-hacking 問題時(shí)注定無法逃避的(de)現實。而至于 $N_0$ 可(kě)能的(de)取值範圍，坦白說也(yě)确實取決于研究者的(de)經驗和(hé)對(duì)實證數據的(de)理(lǐ)解。

在 Harvey and Liu (2021b) 的(de)這(zhè)三組參數中，有一些間接的(de)證據更加支持第三組參數（即 $N_0=5000$ ）。例如在前兩組參數中， $p_0$ （真實異象的(de)比例）分(fēn)别爲 29% 和(hé) 12%。如果說 12% 還(hái)姑且 OK，那麽 29% 則顯得(de)太高(gāo)了(le)。而在第三組參數中， $p_0$ 僅爲 6%。另一方面，下(xià)圖繪制了(le)三組參數下(xià)，不同 t-statistics 被發表的(de)概率。在前兩組參數下(xià)，t-statistic = 2.0 的(de)異象被發表的(de)概率高(gāo)達 30% 以上，這(zhè)似乎無法和(hé)“内卷”時(shí)代發表金融學論文的(de)難度相匹配。在第三組參數下(xià)，這(zhè)個(gè)概率降低了(le)一半，僅有不到 15%。

無論如何，不妨将選擇哪組參數留給各位讀者。在本節的(de)最後，我僅以第三組參數（ $N_0=5000$ ）爲例，介紹一些模型的(de)推論。在這(zhè)組參數下(xià)：

1. 5% false discovery rate（FDR）下(xià)的(de) t-statistics 阈值爲 3.0（這(zhè)個(gè)數值和(hé) Harvey, Liu, and Zhu (2016) 一緻）；

2. 在所有被發表的(de)異象中，真實異象的(de)比例爲 62%（他(tā)們正面回答(dá)了(le)第一節討(tǎo)論的(de) p-hacking 研究關心的(de)第一點）；

3. 在所有被發表的(de)異象中，樣本外平均收益的(de)收縮系數爲 36%；如果僅考慮 t-statistics 在 2.0 到 5.0 之間的(de)異象，該系數上升到 53%（他(tā)們正面回答(dá)了(le)第一節討(tǎo)論的(de) p-hacking 研究關心的(de)第二點）。作爲對(duì)比，無論是 36% 還(hái)是 53% 都遠(yuǎn)超過 Chen and Zimmermann (2020) 所主張的(de) 12%。

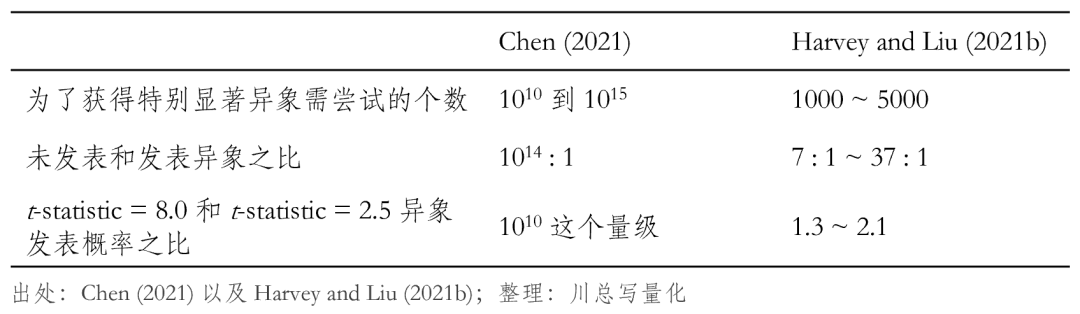
最後的(de)最後，再來(lái)回顧一下(xià) Chen (2021) 的(de)三個(gè)推論，即爲了(le)獲得(de)特别顯著異象所需要的(de)嘗試的(de)次數，未發表和(hé)發表異象之比，t-statistic = 8.0 和(hé) t-statistic = 2.5 異象發表的(de)概率之比。在 Harvey and Liu (2021b) 的(de)模型中，這(zhè)三個(gè)推論的(de)結果如何呢(ne)？下(xià)表總結了(le)在三組不同的(de)參數下(xià)三個(gè)推論的(de)結果，留給小夥伴們去評判。

4 思考

文章(zhāng)最後，我想不妨借助 Harvey and Liu (2021b) 關于未發表異象的(de)推論爲引子，對(duì) p-hacking 問題進行一些思考。由于對(duì)發表過程進行了(le)建模，Harvey and Liu (2021b) 能夠對(duì)未發表的(de)異象進行推論，這(zhè)方面的(de)結果也(yě)頗有價值。具體來(lái)說，他(tā)們考慮了(le) false publication rate 和(hé) false non-publication rate。前者的(de)定義是所有虛假異象中，被錯誤地發表的(de)異象的(de)比例；後者定義是所有真實異象中，沒有被發表的(de)異象的(de)比例。在第三組參數下(xià)，前者爲 1.12%，後者爲 72.93%。我想討(tǎo)論一下(xià)前者。

乍一看 1.12% 似乎很低，但通(tōng)過計算(suàn)并非如此。由于 $N_0=5000$ ， $p_0=0.06$ ，因此所有的(de)虛假異象共有 $5000\times (1-0.06)=4700$ 個(gè)。而這(zhè)其中 1.12% 即 $4700\times 1.12\%=53$ 個(gè)被發表了(le)。正是因爲這(zhè)些被發表的(de)虛假異象，造成了(le)我們今日看到的(de) p-hacking 問題；而識别這(zhè)些被發表的(de)虛假異象 —— 而非去主張 p-hacking 本身無法解釋 t-statistics 很高(gāo)的(de)異象（它當然不能！） —— 才是人(rén)們通(tōng)過研究 p-hacking 應該要解決的(de)問題。

談到 p-hacking，其他(tā)學科對(duì)它的(de)重視其實由來(lái)已久（Ioannidis (2005)），而金融學對(duì)它的(de)重視算(suàn)是比較晚的(de)了(le)。但好消息是，經過過去 5 年的(de)發展，人(rén)們已經意識到這(zhè)個(gè)問題并通(tōng)過各種手段（考慮多(duō)重假設檢驗懲罰，提高(gāo)發表論文的(de)标準，使用(yòng)同樣的(de)數據集在頂刊上發文相互建設性的(de)“硬怼”等）來(lái)降低 p-hacking 的(de)影(yǐng)響。

關于 p-hacking 問題有多(duō)嚴重，學術界以開放的(de)心态來(lái)討(tǎo)論它至關重要。從這(zhè)個(gè)意義上說，本文介紹的(de) Chen (2021) 和(hé) Harvey and Liu (2021b) 沒有誰對(duì)誰錯，都是有益的(de)討(tǎo)論，讓我們可(kě)以從不同的(de)視角立體地審視這(zhè)個(gè)問題。而 Harvey and Liu (2021b) 所表明(míng)的(de)一點就是，因爲 lack of identification，對(duì) p-hacking 的(de)研究确實存在主觀的(de)一面。這(zhè)也(yě)是最近一些文章(zhāng)得(de)到相反結論的(de)原因。與其深究各種（存在問題的(de)）Bayesian 方法，不如承認這(zhè)個(gè)計量上的(de)系統問題，并通(tōng)過合理(lǐ)的(de)主觀判斷得(de)到令人(rén)信服的(de)結論。無論學者們在這(zhè)個(gè)問題上持怎樣不同的(de)立場(chǎng)，關于 p-hacking 的(de)思辨還(hái)遠(yuǎn)沒有走到終點。而如果你要問我，基于最新的(de)研究，是否可(kě)以轉變觀點并認爲被發表的(de)異象大(dà)多(duō)能站得(de)住腳？

我的(de)回答(dá)是：Not so fast!

備注：

[1] 見《在追求 p-value 的(de)道路上狂奔，卻在科學的(de)道路上漸行漸遠(yuǎn)》、《出色不如走運?》、《出色不如走運 (II)?》、《出色不如走運 (III)?》、《出色不如走運 (IV)?》和(hé)《出色不如走運 (V)?》。

[2] 他(tā)們使用(yòng)了(le) Harvey and Liu (2020) 所提出的(de)兩步 bootstrap 法中的(de)第一步 bootstrap。關于這(zhè)篇文章(zhāng)的(de)介紹，見《出色不如走運 (V)?》。

參考文獻

Barras, L., O. Scaillet, and R. Wermers (2010). False discoveries in mutual fund performance: Measuring luck in estimated alphas. Journal of Finance 65(1), 179 – 216.

Chen, A. Y. (2021). The limits of p-hacking: Some thought experiments. Journal of Finance forthcoming.

Chen, A. Y. and T. Zimmermann (2020). Publication bias and the cross-section of stock returns. Review of Asset Pricing Studies 10(2), 249 – 289.

Chordia, T., A. Goyal, and A. Saretto (2020). Anomalies and false rejections. Review of Financial Studies 33(5), 2134 – 2179.

Harvey, C. R. (2017). Presidential address: The scientific outlook in financial economics. Journal of Finance 72(4), 1399 – 1440.

Harvey, C. R. and Y. Liu (2018). Detecting repeatable performance. Review of Financial Studies 31(7), 2499 – 2552.

Harvey, C. R. and Y. Liu (2020). False (and missed) discoveries in financial economics. Journal of Finance 75(5), 2503 – 2553.

Harvey, C. R. and Y. Liu (2021a). Lucky factors. Journal of Financial Economics 141(2), 413 – 435.

Harvey, C. R. and Y. Liu (2021b). Uncovering the iceberg from its tip: A model of publication bias and p-hacking. Working paper.

Harvey, C. R., Y. Liu, and H. Zhu (2016). … and the cross-section of expected returns. Review of Financial Studies 29(1), 5 – 68.

Hou, K., C. Xue, and L. Zhang (2020). Replicating anomalies. Review of Financial Studies 33(5), 2019 – 2133.

Ioannidis, J. P. A. (2005). Why most published research findings are false. PLoS Medicine 2(8), 696 – 701.

Jensen, T. I., B. Kelly, and L. H. Pedersen (2021). Is there a replication crisis in finance? Working paper.

McLean, R. D. and J. Pontiff (2016). Does academic research destroy stock return predictability? Journal of Finance 71(1), 5 – 32.

Martin, I. and S. Nagel (2019). Market efficiency in the age of big data. Working paper.

Yan, X. and L. Zheng (2017). Fundamental analysis and the cross-section of stock returns: A data-mining approach. Review of Financial Studies 30(4), 1382 – 1423.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。

合格投資者聲明(míng)

出色不如走運 (VI) ?