利用(yòng)收益率時(shí)序信息改進 SDF 估計

發布時(shí)間：2021-09-02 | 來(lái)源: 川總寫量化(huà)

作者：石川

摘要：實證結果顯示，因子收益率的(de)時(shí)序信息可(kě)以改進 SDF 估計。

溫馨提示：爲更好的(de)閱讀本文的(de)内容，建議(yì)先熟悉《實證資産定價理(lǐ)論新進展》的(de)第 5 節（估計 SDF）、《FF3 們背後的(de)資産定價理(lǐ)論》、《Which Beta (III)?》以及《尋找 Mean-Variance Frontier》。

The cross-section and time series of stock returns contains a wealth of information about the stochastic discount factor (SDF).

2020 年 5 月(yuè)，Review of Financial Studies 推出了(le)題爲 New Methods in the Cross-Section 的(de)專刊。兩位專刊編輯也(yě)特地寫了(le)一篇同名[1]文章(zhāng)（Karolyi and Nieuwerburgh 2020）介紹這(zhè)期專刊。而上面這(zhè)句話(huà)就出自該文摘要的(de)第一句。它傳遞出了(le)相當多(duō)的(de)信息量。

首先，人(rén)們之所以關心 SDF，是因爲它和(hé) mean-variance efficient frontier 是等價的(de)[2]；後者決定了(le)最大(dà)夏普率，而最大(dà)化(huà)樣本外（條件）夏普率一直都是人(rén)們的(de)目标。所以對(duì) SDF 的(de)估計無疑對(duì)這(zhè)方面有很大(dà)的(de)啓發。在上面這(zhè)句英文中，和(hé)本文最相關的(de)關鍵詞是 time series，即股票(piào)收益率的(de)時(shí)序信息。

最近兩年，在利用(yòng)股票(piào)平均收益截面（cross-section）信息估計 SDF（或者 SDF 的(de)等價物(wù) —— 多(duō)因子模型[3]）方面出現了(le)很多(duō)佳作，其中頗具代表性的(de)見刊的(de)文章(zhāng)包括 2019 和(hé) 2020 年分(fēn)别獲得(de) Journal of Financial Economics Fama-DFA best paper award 的(de)雄文Kelly, Pruitt, and Su (2019) 和(hé) Kozak, Nagel, and Santosh (2020)[4]。不過，利用(yòng)收益率時(shí)序信息來(lái)改進 SDF 估計方面的(de)研究則寥若晨星。

你問爲什(shén)麽，因爲時(shí)序收益率難預測啊！我們來(lái)理(lǐ)一理(lǐ)。根據 Hansen and Jagannathan (1991)，SDF 和(hé)個(gè)股 excess return 滿足如下(xià)關系：

$m_{t+1}=1-b_t^\prime(R_{t+1}-\mbox{E}_t[R_{t+1}])$

其中 $m_{t+1}$ 是 SDF，且由于 $R_{t+1}$ 表示超額收益，因此滿足 $\mbox{E}_t[m_{t+1}R_{t+1}]=0$ 。如果從上式出發，則意味著(zhe)想要更好的(de)估計 SDF，就需要對(duì)個(gè)股收益率進行時(shí)序預測。但這(zhè)無疑是很困難的(de)。因此，有必要把上式進行簡化(huà)。大(dà)量實證研究表明(míng)，股票(piào)的(de)收益率和(hé)各種公司特征（firm characteristics）相關，因此可(kě)以利用(yòng)有限個(gè)公司特征把上式中的(de) $b_t$ —— $t$ 期 SDF 對(duì)股票(piào)的(de) loading 向量 —— 轉化(huà)爲如下(xià)的(de)形式：

$b_t=C_t\delta_t$

其中 $C_t$ 是 $N\times K$ 階矩陣，代表 $N$ 個(gè)股票(piào)在 $K$ 個(gè)公司特征上的(de)取值，而 SDF 的(de)表達式轉化(huà)爲：

$m_{t+1}=1-\delta_t^\prime(F_{t+1}-\mbox{E}_t[F_{t+1}])$

由上述對(duì) $b_t$ 的(de)假設可(kě)知， $F_{t+1}$ 和(hé) $R_{t+1}$ 滿足 $F_{t+1}=C_t’R_{t+1}$ 。看到這(zhè)裏就一目了(le)然了(le)， $F_{t+1}$ （ $K\times 1$ 階向量）代表了(le) $K$ 個(gè) managed portfolios 的(de)收益率 —— 每個(gè)組合都是以 $C_t’$ 的(de)某一行（即原始 $C_t$ 的(de)某一列，即某個(gè)公司特征）爲權重的(de)多(duō)空組合。而在上式中， $\delta_t$ 是 SDF 對(duì)這(zhè)些組合的(de) loading 向量。通(tōng)過這(zhè)個(gè)變化(huà)，我們把 SDF 和(hé) $K$ 個(gè)基于公司特征構造的(de)投資組合 —— 因子！—— 聯系起來(lái)了(le)。由資産定價原理(lǐ)可(kě)知， $t$ 期 SDF 的(de)最優權重爲：

$\displaystyle\delta_t=\Sigma^{-1}_{F,t}\mbox{E}_t[F_{t+1}]$

其中， $\Sigma_F$ 爲因子的(de)協方差矩陣。那麽，我們是否距離利用(yòng)時(shí)序信息更接近了(le)呢(ne)？在上述最優解中，爲了(le)更好的(de)估計 SDF，需要估計時(shí)變的(de)因子預期收益率。這(zhè)件事兒(ér)又有另一個(gè)令人(rén)興奮的(de)名字：因子擇時(shí)。但是因子擇時(shí)何其容易？尤其當因子的(de)個(gè)數 $K$ 很大(dà)的(de)時(shí)候。是否還(hái)有辦法從縮減因子個(gè)數的(de)角度把問題進一步簡化(huà)呢(ne)？好消息是，答(dá)案是肯定的(de)。我們請出第二個(gè)武器：Kozak, Nagel, and Santosh (2018)[5]。Kozak, Nagel, and Santosh (2018) 的(de)研究表明(míng)，在不存在無風險套利機會的(de)假設下(xià)，那些能夠解釋資産共同運動（即協方差矩陣）的(de)因子同樣能夠解釋資産的(de)預期超額收益。在這(zhè)個(gè)結論下(xià)，隻需要把上述因子理(lǐ)解成資産，然後對(duì)它們的(de)協方差矩陣做(zuò) PCA。由于前幾個(gè)主成分(fēn)極大(dà)的(de)解釋了(le)這(zhè)些因子的(de)共同運動，因此它們也(yě)将解釋因子的(de)預期收益。在這(zhè)個(gè)假設下(xià)，對(duì) SDF 的(de)估計可(kě)以進一步簡化(huà)爲：

$m_{t+1}\approx 1-\gamma^\prime(Z_{t+1}-\mbox{E}_t[Z_{t+1}])$

其中 $Z_{t+1}$ 表示由若幹主成分(fēn)構成的(de)投資組合的(de)收益率向量，而 SDF 最優權重爲：

$\displaystyle\gamma_t=\Sigma^{-1}_{Z,t}\mbox{E}_t[Z_{t+1}]$

将其帶回 SDF 的(de)表達式，就可(kě)以得(de)到利用(yòng)了(le)時(shí)序信息的(de) SDF 估計：

$m_{t+1}\approx 1-\mbox{E}_t[Z_{t+1}]\Sigma_{Z,t}^{-1}(Z_{t+1}-\mbox{E}_t[Z_{t+1}])$

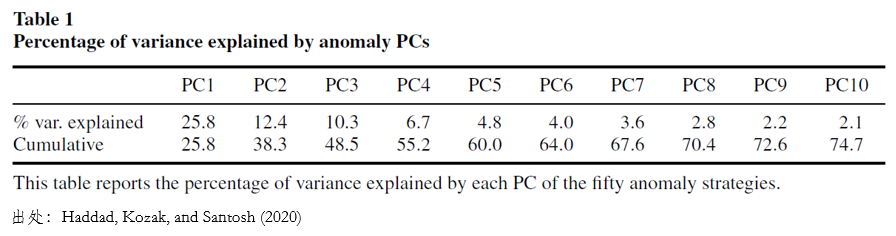
我們來(lái)回顧一下(xià)上述兩步走，來(lái)看看是怎麽得(de)到的(de)最終的(de) SDF 的(de)估計。第一步把股票(piào)收益率轉化(huà)爲因子的(de)收益率（每個(gè)因子組合是按照(zhào) firm characteristic 構造的(de) managed portfolio），并指出通(tōng)過對(duì)因子收益率擇時(shí)在理(lǐ)論上可(kě)以更好的(de)估計 SDF；而第二步中将上述因子視作資産，進一步通(tōng)過 PCA 将需要估計的(de)時(shí)變收益率個(gè)數從 $K$ 個(gè)因子轉化(huà)成比 $K$ 小的(de)多(duō)的(de)有限個(gè)主成分(fēn)的(de)個(gè)數，使得(de)擇時(shí)成爲可(kě)能。上述推論意味著(zhe)，一旦能夠比較準确地預測 $\mbox{E}_t[Z_{t+1}]$ ，就可(kě)以利用(yòng)時(shí)序信息更好的(de)估計 SDF。

那麽實證結果是否支持這(zhè)個(gè)猜想呢(ne)？Haddad, Kozak, and Santosh (2020) 這(zhè)篇發表在本文開篇提到的(de) RFS 專刊上的(de)論文給出了(le)肯定的(de)答(dá)案。在實證中，該文利用(yòng)美(měi)股中常見的(de) 50 個(gè)因子爲出發點。通(tōng)過 PCA 發現，前 10 個(gè)主成分(fēn)就可(kě)以解釋将近 75% 的(de)波動。

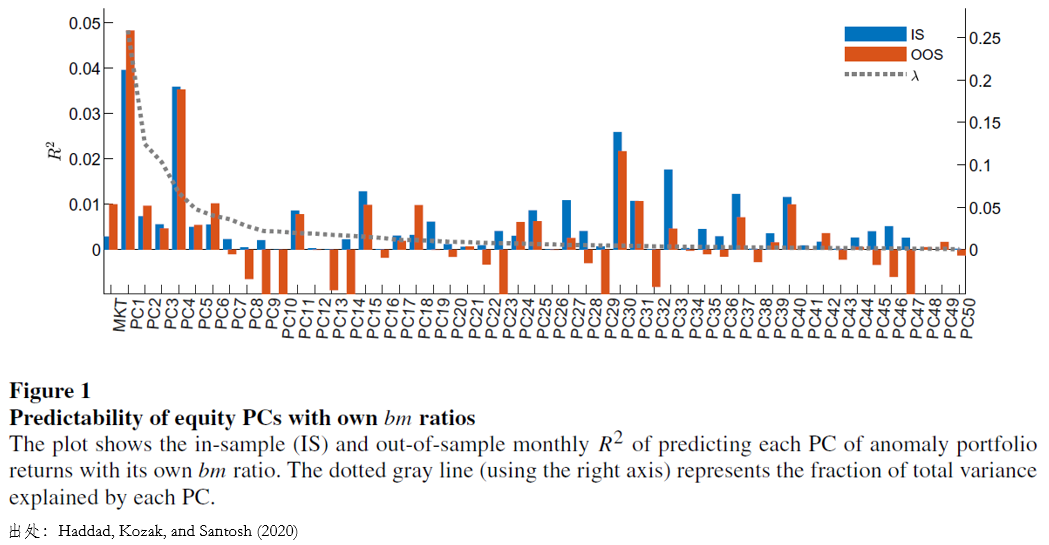
在接下(xià)來(lái)的(de)實證中，他(tā)們最終選擇了(le)前 5 個(gè)主成分(fēn)。再加之市場(chǎng)組合，一共六個(gè)“資産”。它們的(de)收益率就對(duì)應了(le)最終 SDF 表達式中的(de) $Z_{t+1}$ 。爲了(le)預測它們，該文使用(yòng)了(le)一個(gè)最爲基本的(de) predictor —— BM spread。由于每個(gè)主成分(fēn)組合僅僅是原始 50 個(gè)因子的(de)線性組合，因此隻需要先計算(suàn)原始因子的(de) BM spread 再按特征向量爲權重計算(suàn)每個(gè)主成分(fēn)的(de) BM spread。實證數據表明(míng)，BM spread 在樣本外預測 $\mbox{E}_t[Z_{t+1}]$ 的(de)效果很不錯。

另一方面，下(xià)圖給出了(le)利用(yòng) BM spread 預測不同主成分(fēn)在樣本内外的(de)效果（因爲一共有 50 個(gè)原始因子，因此一共有 50 個(gè)主成分(fēn)）。不難看出，實證結果顯示樣本外的(de)預測效果僅僅對(duì)前幾個(gè)主成分(fēn)有效。但這(zhè)并不影(yǐng)響，因爲圖中灰色虛線（右軸）顯示了(le)每個(gè)主成分(fēn)解釋的(de)方差的(de)比例，可(kě)見前幾個(gè)主成分(fēn)極大(dà)解釋了(le)原始因子資産的(de)共同運動。這(zhè)個(gè)實證結果完美(měi)的(de)符合 Kozak, Nagel, and Santosh (2018) 的(de)結論，即隻有前幾個(gè)主成分(fēn)（最能解釋波動的(de)那些）才有用(yòng)。

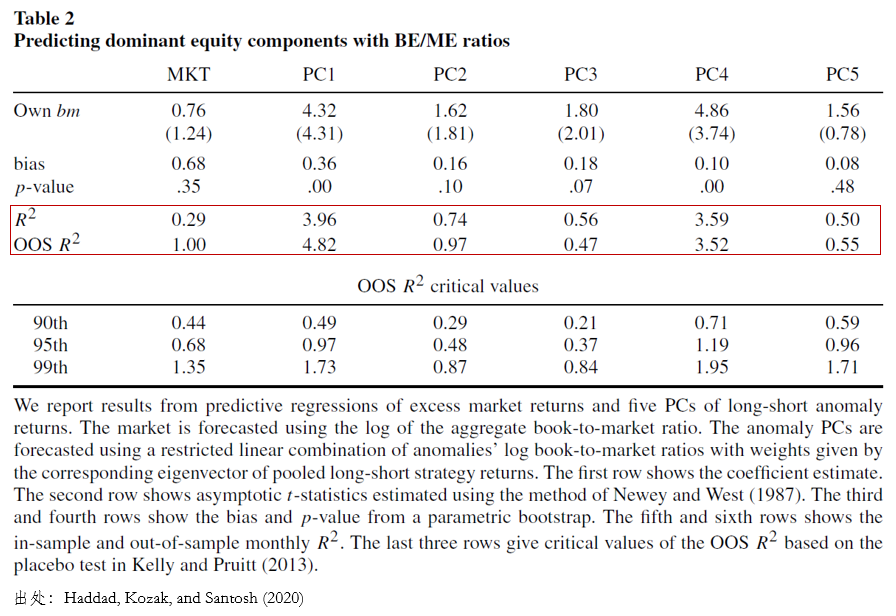
我很欣賞的(de)是，Haddad, Kozak, and Santosh (2020) 并沒有試圖用(yòng)更多(duō)的(de)變量或更複雜(zá)的(de)模型，而是僅僅用(yòng)了(le) BM[6]，來(lái)預測 $\mbox{E}_t[Z_{t+1}]$ 。由資産定價理(lǐ)論可(kě)知，SDF 的(de)最優參數 $\gamma_t$ 同時(shí)是 mean-variance efficient portfolio 的(de)權重，因此可(kě)以通(tōng)過夏普率來(lái)判斷時(shí)序信息是否對(duì)估計 SDF 提供了(le)增量貢獻。爲此，Haddad, Kozak, and Santosh (2020) 考慮了(le)以下(xià)五種不同的(de)處理(lǐ)方式：

Factor investing：不擇時(shí)，用(yòng) unconditional 估計；

Market timing：僅對(duì)市場(chǎng)因子擇時(shí)，對(duì)五個(gè)主成分(fēn)不擇時(shí)；

Factor timing：同時(shí)對(duì)市場(chǎng)和(hé)五個(gè)主成分(fēn)因子擇時(shí)；

Anomaly timing：對(duì)市場(chǎng)不擇時(shí)，對(duì)五個(gè)主成分(fēn)擇時(shí)；

Pure anom. timing：市場(chǎng)權重設爲 0，主成分(fēn)因子權重由 conditional 預期相對(duì) unconditional 預期的(de)偏離決定。

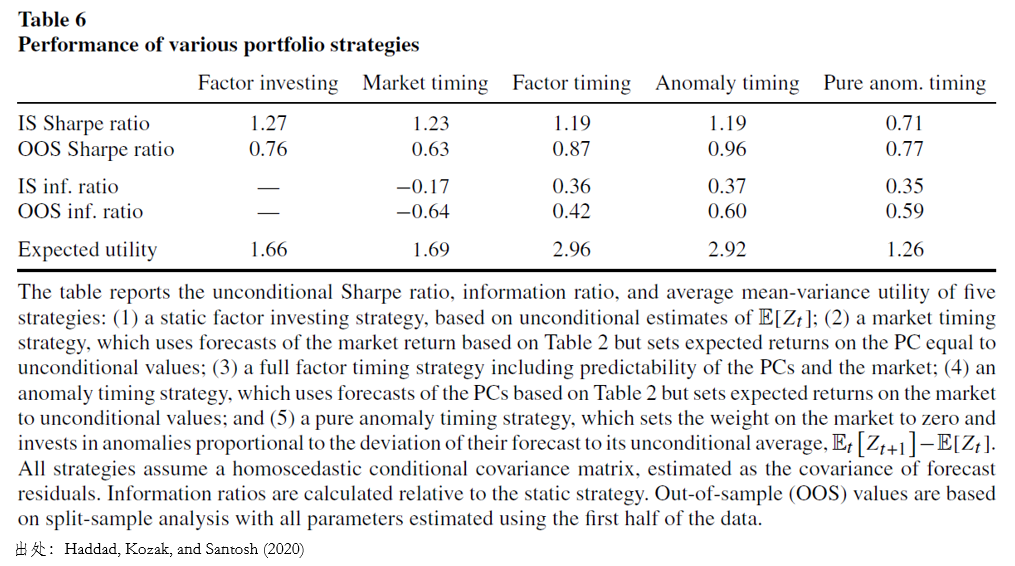
這(zhè)五個(gè)處理(lǐ)方式的(de)樣本内外夏普率如下(xià)表所示。以樣本外夏普率爲例，最好的(de)結果是 anomaly timing 和(hé) factor timing 兩種，這(zhè)說明(míng)利用(yòng)對(duì)因子擇時(shí)是有益的(de)（能夠增大(dà)夏普率）。不過有意思的(de)是，anomaly timing 戰勝了(le) factor timing 則說明(míng)，雖然對(duì)因子擇時(shí)是有益的(de)，但是對(duì)（美(měi)股）市場(chǎng)擇時(shí)（似乎）是徒勞的(de)。

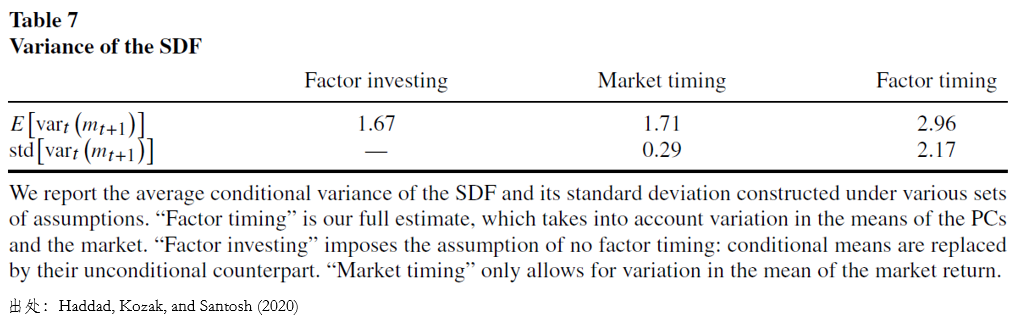
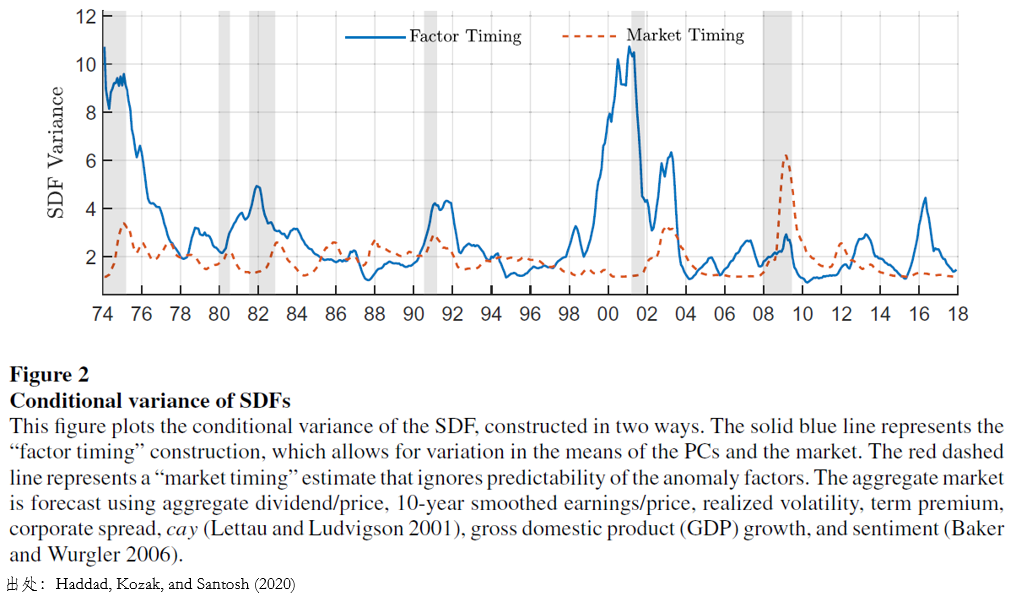
除了(le)從夏普率角度來(lái)評估，我們自然也(yě)關心對(duì) SDF 的(de)估計。由 Hansen and Jagannathan (1991) bond[7]可(kě)知，任何資産的(de)夏普率的(de)上限由 $\sqrt{\mbox{var}_t(m_{t+1})}/\mbox{E}_t[m_{t+1}]$ 決定。在我們的(de)設定下(xià)，由于 $\mbox{E}_t[m_{t+1}]=1$ ，所以任何資産夏普率的(de)上限爲 $\sqrt{\mbox{var}_t(m_{t+1})}$ 。因此，通(tōng)過考察 SDF 的(de)條件方差的(de)大(dà)小，就可(kě)以判斷利用(yòng)時(shí)序信息是否改進了(le) SDF 估計。

作爲比較，Campbell and Cochrane (1999) 對(duì) SDF 方差的(de)估計爲 0 到 1.2 之間。而 Haddad, Kozak, and Santosh (2020) 的(de)估計遠(yuǎn)遠(yuǎn)高(gāo)于這(zhè)個(gè)區(qū)間，也(yě)高(gāo)于不進行因子擇時(shí)的(de)結果（下(xià)圖）。結果顯示，若不進行因子擇時(shí)， $\mbox{var}_t(m_{t+1})$ 的(de)估計爲 1.67，而若隻進行市場(chǎng)擇時(shí)，這(zhè)個(gè)數值僅僅上升至 1.71。而一旦加入因子擇時(shí)， $\mbox{var}_t(m_{t+1})$ 則高(gāo)達 2.96。

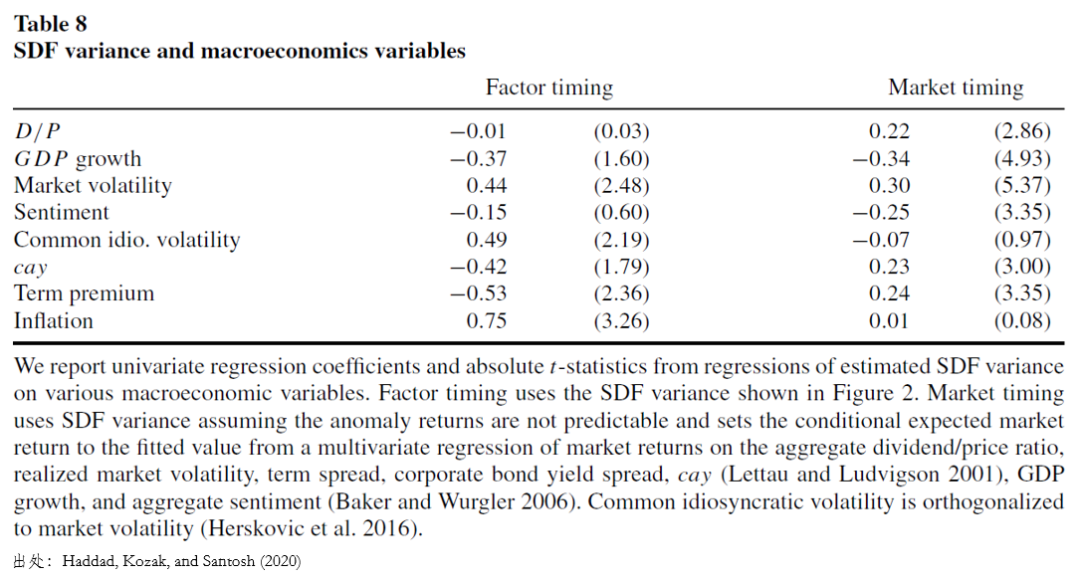
進一步的(de)，下(xià)圖顯示了(le) $\mbox{var}_t(m_{t+1})$ 如何随時(shí)間波動。當考慮因子擇時(shí)後， $\mbox{var}_t(m_{t+1})$ 的(de)波動範圍較僅考慮市場(chǎng)擇時(shí)要大(dà)得(de)多(duō)。這(zhè)說明(míng)如果不考慮因子擇時(shí)，将會丢失掉很多(duō) SDF 的(de)信息。

最後，該文還(hái)研究了(le) SDF 方差和(hé)宏觀經濟之間的(de)關系（下(xià)圖）。不過，幾位作者也(yě)強調，這(zhè)部分(fēn)研究是偏實證性質的(de)。人(rén)們不應急于從回歸系數的(de)正負中盲目得(de)出因果推斷，而是應該以這(zhè)些客觀存在的(de)實證數據爲起點，更好的(de)研究 SDF 和(hé)股票(piào)預期收益的(de)截面差異。

以上就是 Haddad, Kozak, and Santosh (2020) 一文的(de)核心結果。其實，這(zhè)篇文章(zhāng)的(de)标題正是 Factor Timing —— 因子擇時(shí)。然而，我沒有選擇因子擇時(shí)作爲這(zhè)篇小文的(de)标題。其原因是，這(zhè)四個(gè)字實在是太火，我怕一些小夥伴會被這(zhè)個(gè)标題吸引進來(lái)，但在看完後卻留下(xià)一句“這(zhè)不是我想要的(de)”。正如當初我看完這(zhè)個(gè)這(zhè)篇論文的(de)标題就激動的(de)讀下(xià)去，但卻發現它的(de)内容 —— 雖然夠硬核 —— 但是并不是你我心中想象的(de)那種因子擇時(shí)（RFS 畢竟不是 JPM……），你懂(dǒng)的(de)。

Anyway，Campbell Harvey 曾說過，因子擇時(shí)這(zhè)件事兒(ér)雖然非常難，但卻是值得(de)研究。因此，雖然是從估計 SDF 入手，但考慮到 SDF 和(hé) mean-variance efficient frontier 以及多(duō)因子模型的(de)等價性，該文的(de)實證結果以及通(tōng)過 PCA 的(de)處理(lǐ)方式依然能給我們啓發。

最後，再忍不住吐槽一句：也(yě)許不久的(de)将來(lái)，我們就能看到有人(rén)把 A 股的(de)數據套在相似的(de)方法中，然後搖身一變成爲另一篇（次）頂刊論文也(yě)不一定，就像最近剛被 JFE 接收的(de)某篇（還(hái)是賣個(gè)關子吧）。

備注：

[1] 不完全一樣，論文的(de)名字是 New methods for the cross-section of returns，專刊标題是 New methods in the cross-section。

[2] 見《尋找 Mean-Variance Frontier》。

[3] 見《FF3 們背後的(de)資産定價理(lǐ)論》。

[4] 忍不住吐個(gè)槽，這(zhè)兩篇真是 JFE 這(zhè)兩年在資産定價方面的(de)扛把子，其它的(de)大(dà)部分(fēn)……

[5] 見《Which Beta (III) ?》。

[6] 當然，我們僅僅看到了(le)發表出來(lái)的(de)版本。

[7] 見《尋找 Mean-Variance Frontier》。

參考文獻

Campbell, J. Y. and J. H. Cochrane (1999). By force of habit: A consumption-based explanation of aggregate stock market behavior. Journal of Political Economy 107(2), 205 – 251.

Karolyi, G. A. and S. V. Nieuwerburgh (2020). New methods for the cross-section of returns. Review of Financial Studies 33(5), 1879 – 1890.

Kelly, B. T., S. Pruitt, and Y. Su (2019). Characteristics are covariances: A unified model of risk and return. Journal of Financial Economics 134(3), 501 – 524.

Kozak, S., S. Nagel, and S. Santosh (2018). Interpreting factor models.Journal of Finance 73(3), 1183 – 1223.

Kozak, S., S. Nagel, and S. Santosh (2020). Shrinking the cross-section. Journal of Financial Economics 135(2), 271 – 292.

Haddad, V., S. Kozak, and S. Santosh (2020). Factor timing. Review of Financial Studies 33(5), 1980 – 2018.

Hansen, L. P. and R. Jagannathan (1991). Implications of security market data for models of dynamic economics. Journal of Political Economy 99(2), 225 – 262.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。

合格投資者聲明(míng)

利用(yòng)收益率時(shí)序信息改進 SDF 估計