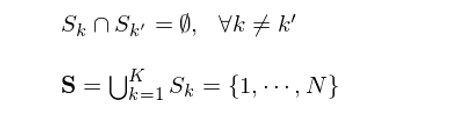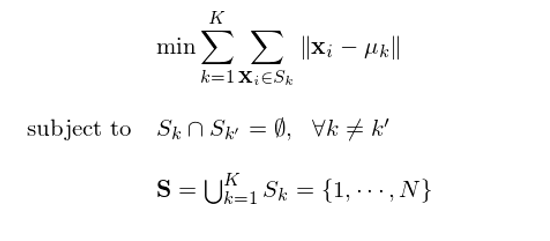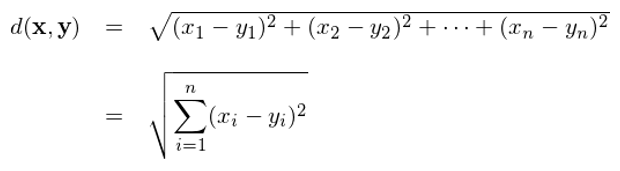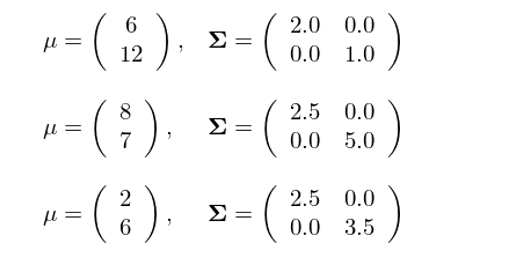用(yòng) K-means 聚類做(zuò)市場(chǎng)狀态分(fēn)析 —— 大(dà)陽線之後更危險？

作者：石川

1 無監督聚類

無監督學習(xí)（unsupervised learning）是機器學習(xí)中的(de)三大(dà)類問題之一，另外兩類分(fēn)别爲監督學習(xí)（supervised learning）和(hé)強化(huà)學習(xí)（reinforcement learning）。在無監督學習(xí)問題中，對(duì)于給定的(de)觀測數據無需（也(yě)沒有）已知的(de)響應（response），而是希望分(fēn)析出觀測數據本身的(de)結構。在無監督學習(xí)中，聚類（clustering）和(hé)降維（dimension reduction）是主要的(de)兩大(dà)應用(yòng)場(chǎng)景。

無監督聚類的(de)目的(de)是将觀測點按照(zhào)它們的(de)特征分(fēn)成若幹個(gè)子集——這(zhè)些子集又稱爲簇（cluster）——以使得(de)每一簇内的(de)觀測點有相似的(de)特性，而不同簇之間的(de)觀測點有不同的(de)特性。聚類分(fēn)析的(de)算(suàn)法有很多(duō)；其中一個(gè)常見且有效的(de)算(suàn)法是 K-means 聚類（譯作 K-均值聚類），其中 K 代表簇的(de)個(gè)數。今天我們就來(lái)說說 K-means 聚類，它在量化(huà)投資領域有很多(duō)應用(yòng)。爲了(le)說明(míng)這(zhè)一點，本文除了(le)介紹該算(suàn)法外，還(hái)會以上證指數的(de)價格數據爲例說明(míng)如何利用(yòng)該算(suàn)法進行市場(chǎng)狀态監測（regime detection）。

2 K-means

K-means 聚類是一種硬聚類（hard clustering）算(suàn)法。所謂硬聚類就是說每一個(gè)樣本點都必須“非此即彼”的(de)被分(fēn)到某一個(gè)簇中。與硬聚類對(duì)應的(de)是軟聚類（soft clustering）。針對(duì)每一個(gè)樣本點，軟聚類算(suàn)法計算(suàn)該點屬于不同簇的(de)概率，這(zhè)是一種模糊（fuzzy）的(de)概念，它不要求樣本點和(hé)簇之間“非此即彼”的(de)映射，而是允許樣本點以不同的(de)概率所屬于不同的(de)簇。

假設 n 維空間中共有 N 個(gè)觀測數據。在數學上，硬聚類意味著(zhe) K 個(gè)簇将該 n 維度空間劃分(fēn)爲 K 個(gè)互斥的(de)區(qū)域，每個(gè)觀測點屬于且僅屬于這(zhè) K 個(gè)簇中的(de)某一個(gè)。令 S_k 代表簇 k，k 屬于｛1, …, K｝，不同的(de)簇 S_k 之間滿足如下(xià)關系：

這(zhè)兩個(gè)式子說明(míng)硬聚類對(duì)空間的(de)劃分(fēn)滿足 MECE 原則，即 Mutually Exclusive（上面第一個(gè)式子）, Collectively Exhaustive（上面第二個(gè)式子）。下(xià)圖是一個(gè) K-means 聚類的(de)示意圖。圖中不同的(de)顔色代表著(zhe) 10 個(gè)簇；每一個(gè)黑(hēi)點代表一個(gè)觀測點。每個(gè)簇内的(de)白色叉子代表該簇的(de)質心。這(zhè)個(gè)圖的(de)意思是，如果我們有下(xià)圖中的(de)那些觀測點，想采用(yòng) K-means 聚類将它們分(fēn)爲 10 個(gè)子集，那麽就會得(de)到如下(xià)的(de)結果。

下(xià)面來(lái)具體說說 K-means 算(suàn)法。該算(suàn)法的(de)目标是，對(duì)于給定的(de)簇個(gè)數 K，找到關于樣本空間的(de)最優化(huà)分(fēn)S =｛S_1, …, S_K｝，使得(de)簇内差異（within-cluster variation）最小。簇内差異被定義爲簇内的(de)每一個(gè)點到該簇質心的(de)距離的(de)平方和(hé)，因此簇内差異又稱爲簇内平方和(hé)（within-cluster sum of squares）。由于質心代表著(zhe)均值，這(zhè)也(yě)是 K-means 聚類名字中 mean 一詞的(de)含義。在數學上，該優化(huà)問題可(kě)以表示爲：

其中，μ_k 代表簇 k 的(de)質心向量，它和(hé)觀測點一樣是 n 維向量。表達式 ||x_i - μ_k|| 代表簇 k 内的(de)第 i 個(gè)點到質心 μ_k 的(de)歐氏距離。

對(duì)該優化(huà)問題求解，就可(kě)以得(de)到最優的(de)劃分(fēn) S =｛S_1, …, S_K｝。不幸的(de)是，尋找該問題的(de)全局解（global optimum）是 NP-hard（簡單的(de)理(lǐ)解就是複雜(zá)度太高(gāo)，讓計算(suàn)機硬來(lái)也(yě)算(suàn)不出來(lái)）。所幸的(de)是，可(kě)以使用(yòng)啓發式算(suàn)法找到局部解（local optimum）。該啓發式算(suàn)法分(fēn)爲兩部，思路如下(xià)。

值得(de)一提的(de)是，局部解十分(fēn)依賴于求解過程的(de)初始值。且由于不知道全局解是什(shén)麽，我們沒法證明(míng)局部解就是最優的(de)。爲了(le)盡可(kě)能降低這(zhè)個(gè)問題的(de)影(yǐng)響，可(kě)以多(duō)次使用(yòng)該啓發式算(suàn)法找到不同的(de)局部解，然後從它們中間找到最小的(de)，作爲最終的(de)解。

3 K-means 的(de)不足

在将 K-means 聚類應用(yòng)于量化(huà)投資之前，有必要知道它的(de)不足。具體來(lái)說，特别是針對(duì)金融數據，它有以下(xià)四點不足之處：

4 K 的(de)取值

聚類分(fēn)析是爲了(le)挖掘觀測數據自身的(de)結構。如果我們在事前從業務的(de)角度對(duì)數據的(de)結構有一個(gè)認知、并以此來(lái)選取簇的(de)個(gè)數，那麽聚類分(fēn)析的(de)結果将會更有意義。反之，如果我們對(duì)待分(fēn)析的(de)數據一無所知，盲目的(de)選擇K的(de)取值，那麽得(de)到的(de)很可(kě)能是無意義的(de)分(fēn)析結果。

下(xià)面通(tōng)過一個(gè)例子說明(míng)正确選取 K 值的(de)重要性。假設我們有 3 個(gè)二元正态分(fēn)布，它們的(de)均值向量、協方差矩陣分(fēn)别如下(xià)所示：

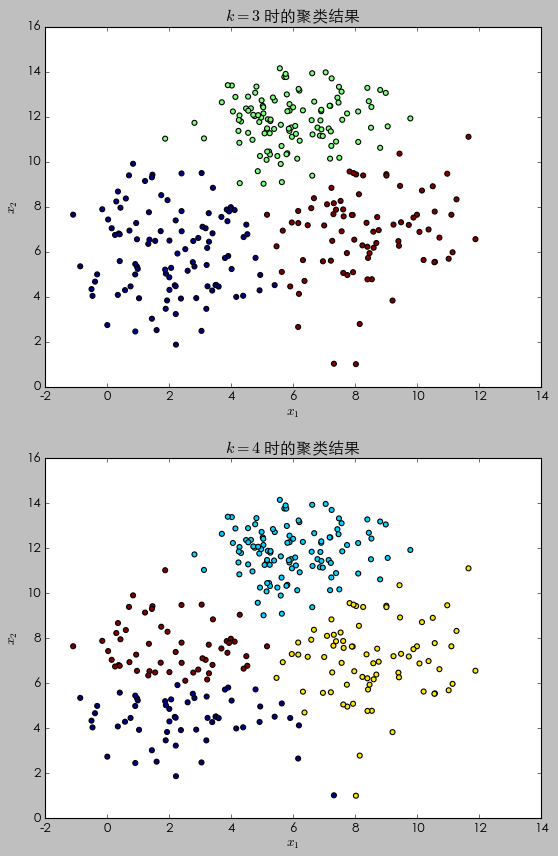
使用(yòng)這(zhè) 3 個(gè)二元正态分(fēn)布在二維空間内各随機生成 100 個(gè)觀測點（即一共有 300 個(gè)點），然後使用(yòng) K-means 聚類對(duì)他(tā)們進行劃分(fēn)。由于在這(zhè)個(gè)例子中，我們知道這(zhè)些點來(lái)自 3 個(gè)不同的(de)二元正态分(fēn)布，因此簇數 K 的(de)正确取值應該爲 3。爲了(le)比較，我們同時(shí)考慮 K = 4 的(de)情況。下(xià)圖展示了(le) K = 3 和(hé) K = 4 時(shí)的(de) K-means 聚類結果。

當 K = 3 時(shí)，這(zhè) 300 個(gè)觀測點被分(fēn)爲了(le) 3 簇。它們的(de)質心基本位于 (2, 6)、(8, 7) 以及 (6, 12) 這(zhè)三個(gè)點附近——即這(zhè)三個(gè)二元正态分(fēn)布的(de)均值點。由于 K = 3 和(hé)這(zhè)些點的(de)内在結構吻合（因爲在這(zhè)個(gè)例子中我們知道這(zhè)些點是來(lái)自這(zhè) 3 個(gè)不同的(de)二元正态分(fēn)布！），所以聚類挖掘出了(le)有效的(de)信息。當 K = 4 時(shí)，這(zhè) 300 個(gè)觀測點被分(fēn)爲了(le) 4 簇。比較兩個(gè)聚類結果可(kě)知，來(lái)自于均值向量 (2, 6)、協方差矩陣 (2.5, 0; 0, 3.5) 這(zhè)個(gè)二元正态分(fēn)布的(de)樣本點被進一步細分(fēn)爲兩個(gè)不同的(de)簇（這(zhè)是因爲 K = 4，因此算(suàn)法必須把所有點分(fēn)爲 4 簇！）。基于這(zhè)樣的(de)結果，我們會認爲這(zhè)兩簇是不同的(de)。但是在這(zhè)裏例子中，它們事實上來(lái)自同一個(gè)分(fēn)布。這(zhè)個(gè)例子說明(míng)，當 K 的(de)取值不當時(shí)，我們有可(kě)能從聚類的(de)結果中得(de)出錯誤的(de)推斷。因此，在使用(yòng) K-means 聚類之前，如能對(duì)待分(fēn)析的(de)數據有一定的(de)了(le)解，并能從業務的(de)角度判斷出合适的(de)簇數 K，将大(dà)大(dà)提高(gāo)聚類分(fēn)析結果的(de)可(kě)靠性。

5 用(yòng) K-means 進行市場(chǎng)狀态監測

本節使用(yòng)一個(gè)簡單的(de)例子将 K-means 聚類應用(yòng)于量化(huà)投資領域。我們使用(yòng)上證指數日線的(de)開盤、最高(gāo)、最低、收盤價（即 OHLC 數據）來(lái)描述市場(chǎng)所處的(de)（未知）狀态，通(tōng)過聚類将不同的(de)交易日劃分(fēn)到不同的(de)市場(chǎng)狀态中，并在聚類的(de)結果上進行進一步的(de)推斷。交易日的(de)時(shí)間跨度爲過去 5 年。在這(zhè)樣的(de)設定下(xià)，每一個(gè)交易日的(de) OHLC 數據就是一個(gè)觀測點。爲了(le)不同的(de)交易日的(de)價格數據有可(kě)比性，有必要進行标準化(huà)處理(lǐ)。爲此，使用(yòng)每日的(de)開盤價對(duì)其他(tā)三個(gè)價格進行标準化(huà)，得(de)到 H/O，L/O，C/O，即最高(gāo)價和(hé)開盤價之比、最低價和(hé)開盤價之比、以及收盤價和(hé)開盤價之比。标準化(huà)後，每一個(gè)觀測點實際上是一個(gè)三維向量。接下(xià)來(lái)就是确定簇數 K 的(de)取值。在本例中，每一簇便代表了(le)市場(chǎng)的(de)一種狀态。從這(zhè)個(gè)角度出發，我們假設 K 的(de)取值爲 4，即市場(chǎng)存在 4 種狀态。

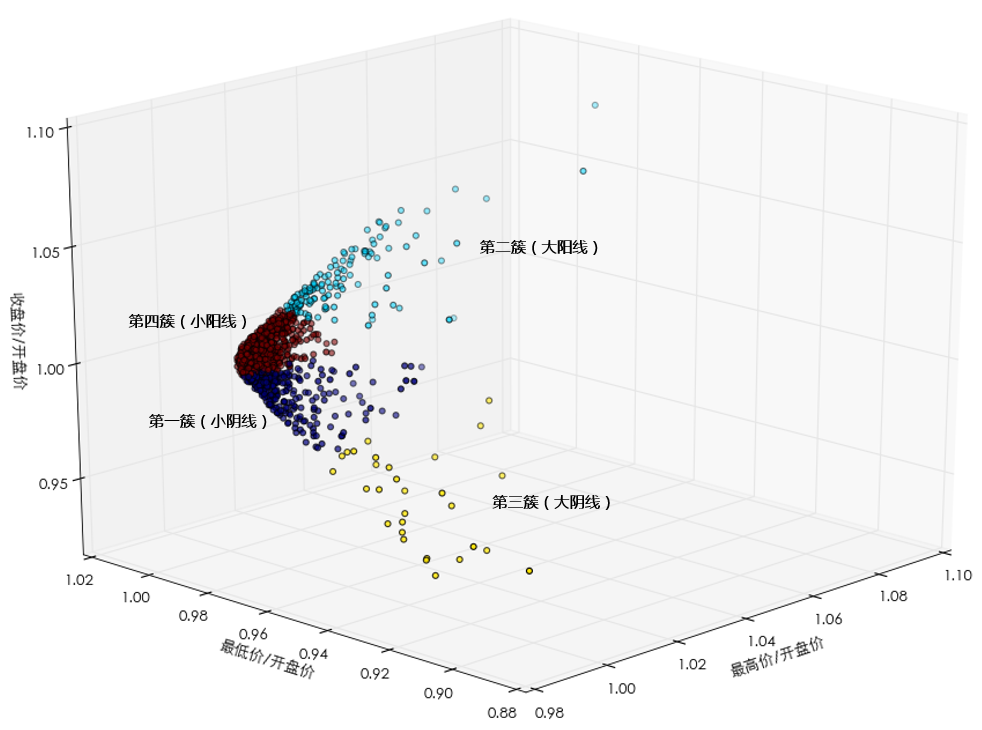
由于觀測點都是三維的(de)，因此可(kě)以方便的(de)在三維空間畫(huà)出聚類的(de)結果。以不同顔色表示不同的(de)簇，這(zhè) 4 簇的(de)聚類結果如下(xià)圖所示。大(dà)部分(fēn)觀測點都圍繞在 (1.0, 1.0, 1.0) 附近，它們構成了(le)兩簇 —— 小陽線和(hé)小陰線；少量的(de)觀測點在遠(yuǎn)離 (1.0, 1.0, 1.0) 的(de)位置，構成另外兩簇 —— 大(dà)陽線和(hé)大(dà)陰線。

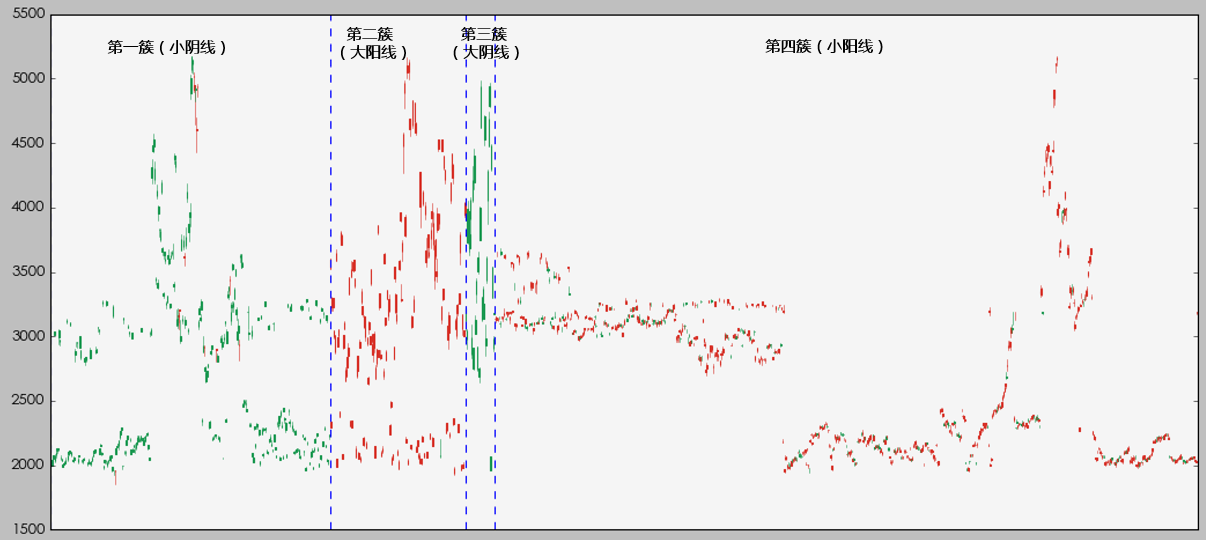
如果我們按照(zhào)簇把每個(gè)交易日的(de) K 線畫(huà)出來(lái)，則可(kě)以更清晰的(de)看出簇與簇之間交易日 K 的(de)差異（下(xià)圖）。

從這(zhè)個(gè)圖中可(kě)以看出：

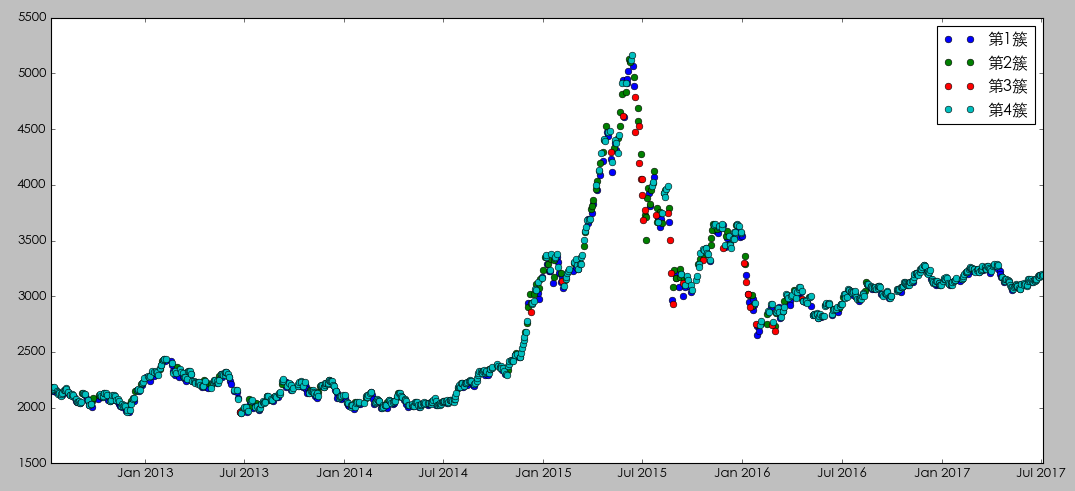
不過這(zhè)個(gè)結果也(yě)清晰的(de)說明(míng)，我們的(de)樣本是嚴重的(de)不均衡的(de)，第四簇小陽線内的(de)觀測點遠(yuǎn)超其他(tā)三簇。樣本嚴重不均衡對(duì)所有的(de)機器學習(xí)算(suàn)法都是一個(gè)挑戰。我們會在下(xià)面再談到這(zhè)個(gè)問題。如果按照(zhào)時(shí)間順序把每個(gè)交易日的(de)市場(chǎng)狀态畫(huà)出來(lái)，則得(de)到下(xià)圖。

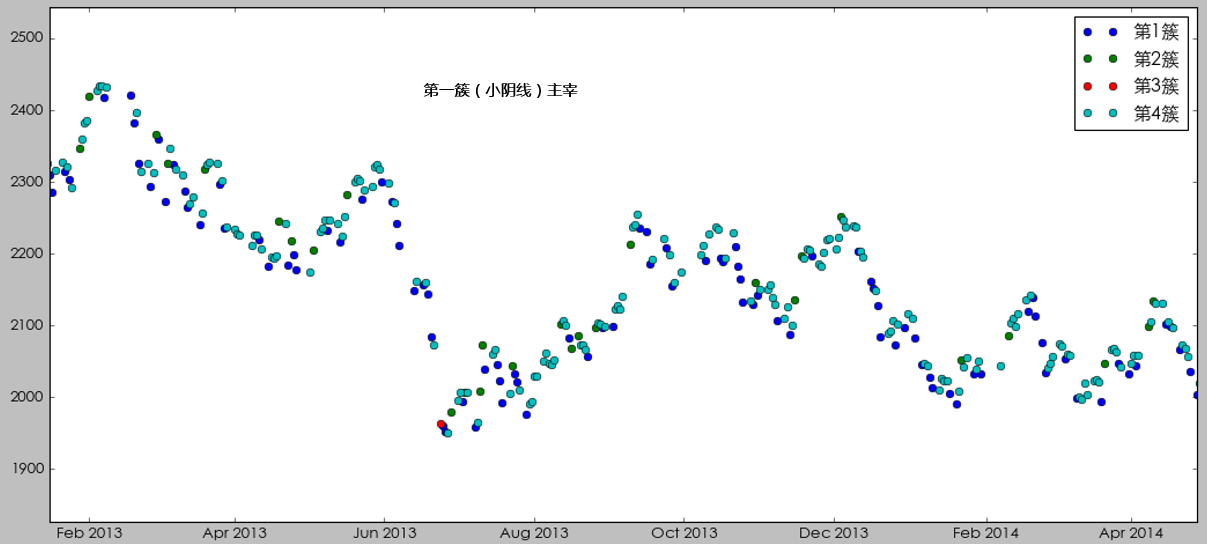
我們分(fēn)幾個(gè)不同的(de)時(shí)期來(lái)仔細看看。在 2014 年底牛市啓動之前，市場(chǎng)的(de)狀态受第一簇（小陰線）主宰，表現出來(lái)一個(gè)慢(màn)慢(màn)陰跌的(de)态勢。

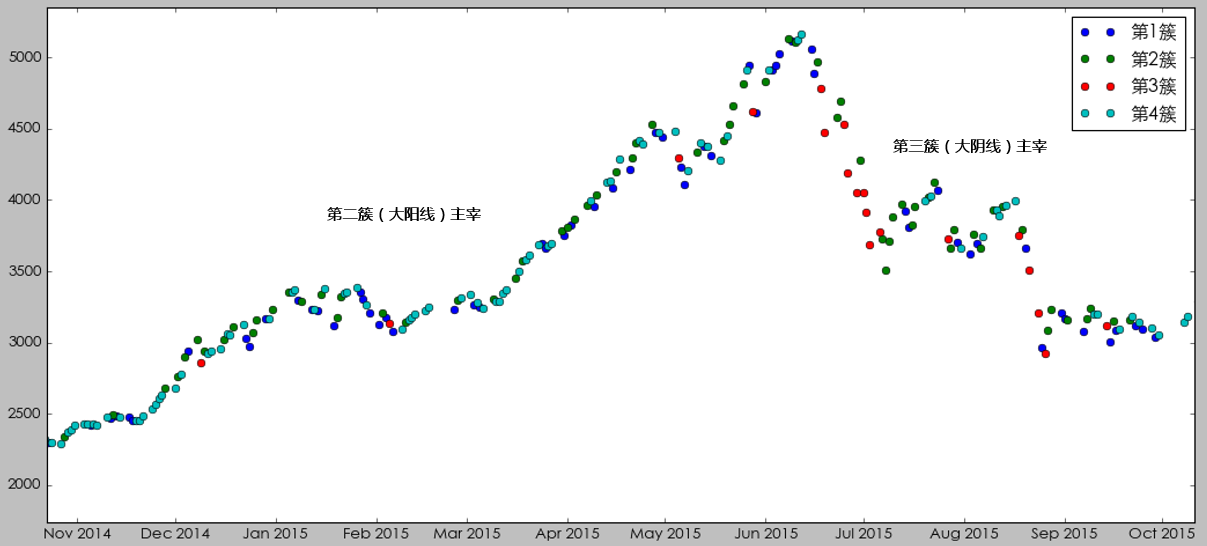
在 2014 年底到 2015 年底這(zhè)個(gè)牛熊周期中，在牛市中市場(chǎng)狀态由第二簇（大(dà)陽線）主宰，而在熊市中市場(chǎng)狀态由第三簇（大(dà)陰線）主宰。

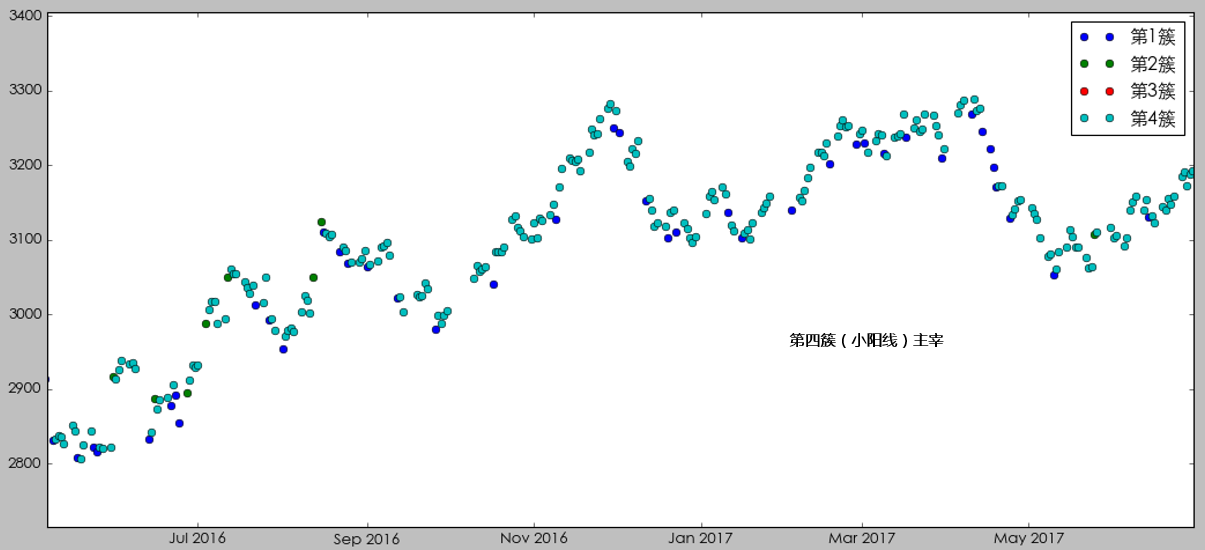
最後，從 2016 年二季度開始，市場(chǎng)狀态由第四簇（小陽線）主宰，呈現出慢(màn)牛的(de)走勢。

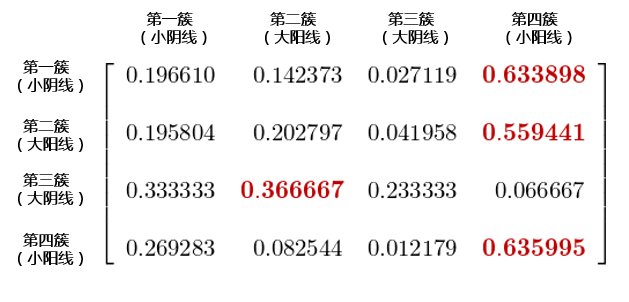
在我們有了(le)每個(gè)交易日的(de)狀态之後，便可(kě)以進行一系列的(de)數據分(fēn)析，得(de)到進一步的(de)推論。這(zhè)其中最有效的(de)應該是求出市場(chǎng)狀态的(de)轉移矩陣，它告訴我們在當前的(de)狀态 i 下(xià)，下(xià)一個(gè)交易日市場(chǎng)将處于狀态 j 的(de)條件概率。這(zhè)對(duì)策略擇時(shí)和(hé)風控會有很大(dà)幫助。基于上面的(de)聚類結果，得(de)到市場(chǎng)狀态的(de)轉移矩陣如下(xià)。其中第 i 行第 j 列的(de)數值表示在今天的(de)市場(chǎng)狀态爲 i 的(de)條件下(xià)，明(míng)天市場(chǎng)狀态爲 j 的(de)條件概率。對(duì)于每一個(gè) i，明(míng)天最有可(kě)能的(de)狀态 j 被用(yòng)紅色粗體表示出來(lái)。這(zhè)個(gè)結果說明(míng)，除了(le)大(dà)陰線外，在其他(tā)三種狀态下(xià)，下(xià)一個(gè)交易日最有可(kě)能出現的(de)都是小陽線，這(zhè)和(hé)前面提到的(de)樣本嚴重不均衡密切相關。

本文的(de)标題提出一個(gè)問題“大(dà)陽線之後更危險？”。這(zhè)個(gè)問題可(kě)以通(tōng)過這(zhè)個(gè)狀态轉移矩陣回答(dá)。如果今天是大(dà)陽線，則下(xià)一個(gè)交易日是大(dà)陰線的(de)條件概率爲4.2%（第二行、第三列的(de)數值）。讓我們再來(lái)看看大(dà)陰線出現的(de)非條件概率。在回測的(de) 1207 個(gè)交易日中，有 30 個(gè)交易日屬于第三簇，因此大(dà)陰線的(de)非條件概率僅爲 2.5%，小于前面這(zhè)個(gè) 4.2% 的(de)條件概率。基于這(zhè)個(gè)結果，我們得(de)出“大(dà)陽之後更危險”的(de)推論。這(zhè)個(gè)結論事實上是符合人(rén)的(de)認知的(de)。這(zhè)是因爲無論大(dà)漲還(hái)是大(dà)跌，都意味著(zhe)波動率的(de)上升；而波動率的(de)上升意味著(zhe)風險的(de)加大(dà)；風險加大(dà)意味著(zhe)大(dà)跌的(de)可(kě)能性增大(dà)。假如上述聚類分(fēn)析的(de)結果是有效的(de)，那麽使用(yòng)這(zhè)個(gè)轉移矩陣可(kě)以回答(dá)很多(duō)類似的(de)問題、得(de)到很多(duō)有益的(de)推論。

6 結語

樣本不足和(hé)樣本不均衡是金融數據的(de)兩大(dà)特色。這(zhè)些對(duì)于 K-means 聚類算(suàn)法在量化(huà)投資中的(de)應用(yòng)提出了(le)嚴峻的(de)挑戰。對(duì)于待分(fēn)析的(de)數據，“如何有效的(de)選取特征？”，“适合的(de)簇數 K 是多(duō)少？”，這(zhè)些都屬于算(suàn)法本身之外的(de)問題，但它們又對(duì)算(suàn)法的(de)分(fēn)析結果至關重要。比如在上面的(de)例子中，使用(yòng) OHLC 數據描述市場(chǎng)狀态是否恰當？K = 4 是否有足夠的(de)依據？要回答(dá)這(zhè)些問題，自然需要更多(duō)的(de)研究。任何機器學習(xí)算(suàn)法都僅僅是工具。在金融領域，核心的(de)問題不是工具的(de)使用(yòng)，而是從對(duì)市場(chǎng)的(de)理(lǐ)解。唯有理(lǐ)解了(le)市場(chǎng)，才能選擇正确的(de)工具。掌握一門算(suàn)法并不需要很長(cháng)的(de)時(shí)間；但要想深刻理(lǐ)解市場(chǎng)則需要時(shí)間的(de)積澱。

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。