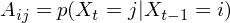從飲食習(xí)慣知天氣冷(lěng)暖 —— 淺談隐馬爾可(kě)夫模型

作者：石川

摘要：無記憶性使得(de)很多(duō)複雜(zá)的(de)問題變得(de)易于分(fēn)析和(hé)計算(suàn)。今天通(tōng)過氣溫和(hé)飲食的(de)例子來(lái)介紹馬爾可(kě)夫和(hé)隐馬爾可(kě)夫模型。

1 引言

明(míng)天的(de)世界隻與今天有關，而與昨天無關。

這(zhè)句話(huà)是對(duì)馬爾可(kě)夫模型的(de)一個(gè)很好的(de)诠釋。在概率論中，馬爾可(kě)夫模型是一個(gè)非常重要的(de)狀态空間随機模型（stochastic state space model）。該模型假設一個(gè)系統或随機變量在下(xià)一時(shí)刻的(de)狀态僅和(hé)當前的(de)狀态有關，而與任何過去的(de)曆史狀态都無關，即當前的(de)狀态已經包括了(le)預測未來(lái)所需的(de)所有信息。這(zhè)個(gè)特性被稱爲馬爾可(kě)夫性質（Markov property），也(yě)被稱爲無記憶性（memorylessness）。馬爾可(kě)夫模型由俄羅斯數學家安德雷 • 馬爾可(kě)夫（Андрей Андреевич Марков）提出。該模型在預測建模方面有著(zhe)廣泛的(de)應用(yòng)。近年來(lái)，也(yě)有越來(lái)越多(duō)的(de)人(rén)将它用(yòng)在量化(huà)投資領域。

根據在時(shí)間上以及在狀态空間中是否連續，馬爾可(kě)夫模型又有不同的(de)版本，比如連續的(de)馬爾可(kě)夫過程（Markov process）和(hé)離散的(de)馬爾可(kě)夫鏈（Markov chain）。本文中，爲了(le)便于介紹，我們考慮最簡單的(de)離散模型，即模型在時(shí)間和(hé)狀态上都是離散的(de)。時(shí)間上離散意味著(zhe)系統僅在特定的(de)時(shí)間點上發生狀态的(de)變化(huà)（比如每小時(shí)或者每天發生一次變化(huà)）；狀态空間上離散意味著(zhe)系統狀态的(de)取值是非連續的(de)。此外我們假設狀态的(de)取值個(gè)數是有限的(de)。離散模型雖然簡單，但在本文最後一節可(kě)以看出，它在量化(huà)投資領域同樣有重要的(de)應用(yòng)價值。

在正常的(de)馬爾可(kě)夫模型中，系統的(de)狀态對(duì)于觀察者來(lái)說是直接可(kě)見的(de)，我們關心的(de)是諸如系統在不同時(shí)刻處于不同狀态的(de)概率這(zhè)類問題。遺憾的(de)是，在一些應用(yòng)中（比如量化(huà)投資中的(de)一些問題），我們并不能直接觀測到系統的(de)狀态——這(zhè)些狀态對(duì)我們來(lái)說是隐形的(de)。雖然無法直接觀測到狀态，但是受這(zhè)些狀态影(yǐng)響的(de)觀測量的(de)取值對(duì)我們來(lái)說是可(kě)見的(de)；我們需要透過這(zhè)些觀測量的(de)取值來(lái)推測系統所處的(de)狀态。這(zhè)樣的(de)模型稱爲隐馬爾可(kě)夫模型（Hidden Markov Models，簡稱 HMM）。

2 馬爾可(kě)夫模型的(de)一個(gè)例子

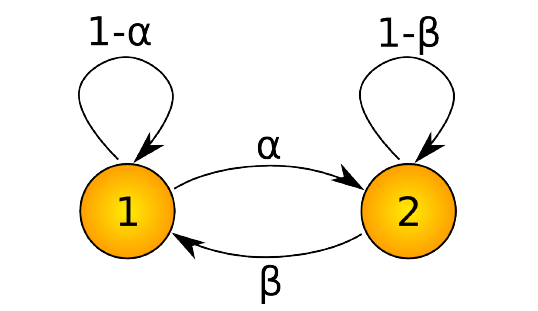
假設我們要分(fēn)析的(de)系統是城(chéng)市 S 的(de)每天的(de)氣溫。爲了(le)簡化(huà)問題，令氣溫分(fēn)爲冷(lěng)和(hé)熱(rè)兩個(gè)狀态。在馬爾可(kě)夫模型的(de)框架下(xià)，該系統有兩個(gè)狀态，且狀态間的(de)轉移由下(xià)面四個(gè)條件概率來(lái)表示：

這(zhè)個(gè)系統可(kě)以由下(xià)面這(zhè)個(gè)馬爾可(kě)夫鏈表示，其中 1 和(hé) 2 分(fēn)别代表了(le)熱(rè)和(hé)冷(lěng)兩個(gè)狀态，箭頭表明(míng)了(le)狀态之間的(de)轉移、旁邊的(de)數字表明(míng)了(le)轉移發生的(de)概率。

這(zhè)四個(gè)條件概率又被稱爲狀态之間的(de)轉移概率。一般的(de)，一個(gè)具有 K 個(gè)狀态的(de)馬爾可(kě)夫過程，對(duì)于所有的(de) i, j ∈ {1, 2, …, K}，其在 t – 1 到 t 時(shí)刻從狀态 i 到狀态 j 的(de)轉移概率便構成了(le)轉移矩陣（transition matrix）中。因此轉移矩陣中第 i 行第 j 列的(de)元素爲：

對(duì)于一個(gè)離散的(de)馬爾可(kě)夫過程來(lái)說，轉移矩陣包括了(le)刻畫(huà)其狀态變換随機性的(de)全部信息。有了(le)轉移矩陣，我們可(kě)以方便的(de)求解各種關于系統狀态的(de)概率問題。比如，在本節的(de)例子中，如果城(chéng)市 S 今天的(de)天氣是熱(rè)，那麽我們可(kě)以方便的(de)計算(suàn)出明(míng)天（乃至任意若幹天之後）天氣情況的(de)概率；我們也(yě)可(kě)以回答(dá)例如未來(lái)五天連續出現天冷(lěng)（或熱(rè)）的(de)概率。總之，有了(le)這(zhè)個(gè)轉移矩陣，一切關于系統狀态的(de)問題都可(kě)以計算(suàn)。

3 隐馬爾可(kě)夫模型的(de)一個(gè)例子

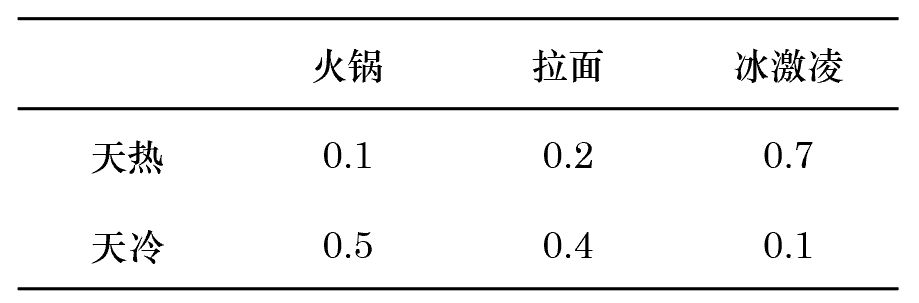
在隐馬爾可(kě)夫模型中，系統的(de)狀态并不是直接可(kě)見的(de)，但受狀态影(yǐng)響的(de)某些觀測量則是可(kě)見的(de)。這(zhè)些觀測量受不同狀态的(de)影(yǐng)響不同，即不同狀态下(xià)，這(zhè)些觀測量有著(zhe)不同的(de)概率分(fēn)布。因此通(tōng)過分(fēn)析觀測量序列，我們可(kě)以對(duì)系統的(de)狀态做(zuò)出判斷。爲了(le)解釋隐馬爾可(kě)夫模型，仍然考慮城(chéng)市 S 的(de)天氣的(de)例子。假設天氣仍然隻有冷(lěng)、熱(rè)兩個(gè)狀态。但與前面例子不同的(de)是，你無法直接獲得(de)關于 S 的(de)天氣信息（比如你不生活在該城(chéng)且沒有它的(de)天氣預報）。 所幸的(de)是，你有一個(gè)好朋友 c 居住在 S 城(chéng)。他(tā)根據當天的(de)天氣情況，每天從火鍋、拉面和(hé)冰激淩三種食品中以不同的(de)概率挑選一種來(lái)吃(chī)，并把吃(chī)了(le)什(shén)麽告訴你。具體的(de)，在不同天氣下(xià)，朋友 c 選擇這(zhè)三種食品的(de)概率如下(xià)。

因此，雖然你不知道 S 城(chéng)的(de)天氣， 但是知道 c 每天的(de)飲食。因此你可(kě)以通(tōng)過朋友的(de)飲食信息判斷 S 城(chéng)的(de)冷(lěng)暖。比如  c 告訴你他(tā)連續吃(chī)了(le)五天火鍋，那麽你可(kě)以判斷出過去五天 S 城(chéng)的(de)天氣很可(kě)能都處于冷(lěng)的(de)狀态，因爲在天冷(lěng)時(shí) c 吃(chī)火鍋的(de)概率遠(yuǎn)大(dà)于天熱(rè)時(shí)。這(zhè)就是隐馬爾可(kě)夫模型要解決的(de)問題之一。

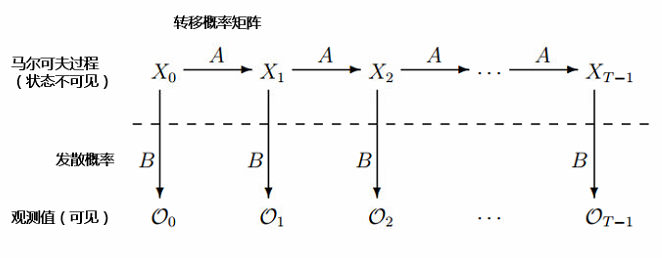
在數學上，隐馬爾可(kě)夫模型如下(xià)圖所示。其内在的(de)馬爾可(kě)夫過程仍然由轉移矩陣 A 來(lái)刻畫(huà)，隻不過狀态對(duì)你來(lái)說它是不可(kě)見的(de)。除了(le) A 之外，狀态與觀測值之間的(de)關系——即觀測值在不同狀态下(xià)不同的(de)概率分(fēn)布——由發散概率（emission probability）B 來(lái)決定。值得(de)一提的(de)是，雖然在本例中，觀測值（火鍋、拉面、冰激淩）在不同狀态（天冷(lěng)、熱(rè)）下(xià)的(de)概率分(fēn)布是離散的(de)，但是這(zhè)個(gè)概率分(fēn)布也(yě)完全可(kě)以是連續的(de)。這(zhè)完全由待考察的(de)問題決定。

在任意時(shí)刻  t，系統處于未知的(de)狀态 X_t，根據對(duì)應的(de)發散概率産生相應的(de)觀測值 O_t，這(zhè)對(duì)于你來(lái)說是可(kě)見的(de)。如何根據觀測值序列來(lái)推測狀态序列，或者如何根據轉移概率和(hé)發散概率計算(suàn)某個(gè)觀測值出現的(de)概率，這(zhè)些都是隐馬爾可(kě)夫模型想要回答(dá)的(de)問題。

4 三類問題

在隐馬爾可(kě)夫模型（HMM）中，視要解決的(de)問題而定，A 和(hé) B 對(duì)你來(lái)說可(kě)以是已知的(de)或未知的(de)。具體的(de)，我們可(kě)以解決三類問題。

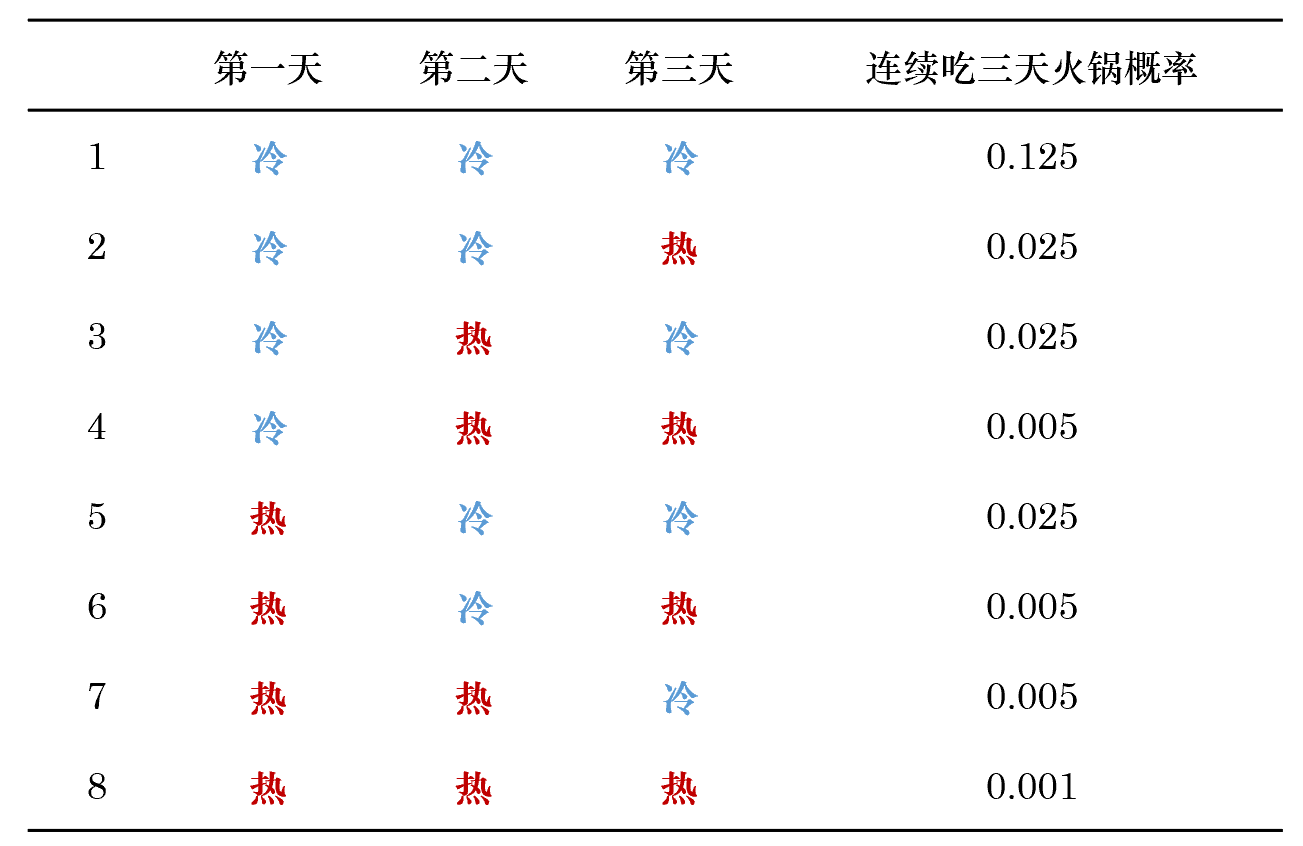
對(duì)于量化(huà)投資來(lái)說，在建模時(shí)，A 和(hé) B 基本上都是未知的(de)，因此第三類問題是我們最關心的(de)。下(xià)面分(fēn)别對(duì)這(zhè)三類問題做(zuò)簡要介紹。前兩類問題看似非常接近，都是知道 A，B 和(hé) O，然後求一個(gè)概率。但是他(tā)們又略有不同。我們用(yòng)上一節的(de)那個(gè)氣溫和(hé)飲食的(de)例子做(zuò)一個(gè)解釋。假設連續三天 c 的(de)飲食都是火鍋；而這(zhè)三天的(de)天氣冷(lěng)、熱(rè)狀态一共有 8 種可(kě)能，如下(xià)表所示。

在這(zhè) 8 中情況下(xià)，朋友 c 均有可(kě)能連續吃(chī)三天火鍋，隻不過在不同的(de)狀态序列下(xià)，他(tā)連續吃(chī)三天火鍋的(de)概率不同（概率見上表）。如果連續三天都很冷(lěng)，那麽他(tā)都吃(chī)火鍋的(de)概率爲 0.125，如果三天都很熱(rè)，那麽他(tā)吃(chī)火鍋的(de)概率則僅爲 0.001。在第一類問題中，我們不關心産生吃(chī)三天火鍋這(zhè)個(gè)觀測序列的(de)具體狀态序列；我們關心的(de)是在所有可(kě)能的(de)狀态序列下(xià)，發生這(zhè)個(gè)觀測序列的(de)總的(de)概率。這(zhè)個(gè)概率就是上面八種情況的(de)加權總和(hé)，權重爲每個(gè)狀态序列出現的(de)概率，這(zhè)個(gè)概率可(kě)以通(tōng)過狀态的(de)初始概率分(fēn)布以及轉移矩陣 A 求出。在第二類問題中，我們關心的(de)是，在所有能夠産生連吃(chī)三天火鍋這(zhè)個(gè)觀測序列的(de)狀态序列中，産生該觀測序列的(de)可(kě)能性最大(dà)的(de)那個(gè)——即在何種狀态序列下(xià)，發生這(zhè)個(gè)觀測序列的(de)概率最高(gāo)。例如在上面這(zhè)個(gè)問題中，最有可(kě)能産生連吃(chī)三天火鍋的(de)氣溫狀态序列是冷(lěng)冷(lěng)冷(lěng)。

對(duì)于這(zhè)兩類問題的(de)求解，上面這(zhè)個(gè)例子也(yě)許也(yě)許給你一個(gè)錯覺：隻要羅列出狀态所有的(de)排列組合就行了(le)。但不要忘了(le)，這(zhè)個(gè)例子中僅考慮了(le)兩個(gè)狀态和(hé)三個(gè)觀測值，因此僅有 2^3 = 8 種情況。在實際問題中，如果有 N 個(gè)狀态和(hé) T 個(gè)觀測值，可(kě)能的(de)狀态序列爲 N^T 個(gè)。因此，對(duì)于計算(suàn)機來(lái)說，窮舉法的(de)計算(suàn)量級爲 O(N^T)，當 N 和(hé)/或 T 很大(dà)時(shí)，列出所有的(de)可(kě)能是低效甚至是不切實際的(de)。好消息是，我們可(kě)以使用(yòng)更有效的(de)算(suàn)法來(lái)代替窮舉法。對(duì)于第一類問題，一個(gè)有效的(de)算(suàn)法爲向前算(suàn)法（forward algorithm）；對(duì)于第二類問題，一個(gè)有效的(de)算(suàn)法爲維特比算(suàn)法（Viterbi algorithm）。這(zhè)兩種算(suàn)法都屬于動态規劃算(suàn)法，計算(suàn)量級要比窮舉的(de)計算(suàn)量級小得(de)多(duō)。感興趣的(de)讀者可(kě)以進一步參考相關資料。

最後，來(lái)看第三類問題。它事實上是一個(gè)模型訓練問題。HMM 就是我們的(de)模型，觀測序列就是我們的(de)數據。機器學習(xí)需要通(tōng)過數據訓練模型，得(de)到 HMM 的(de)最佳參數 A 和(hé) B。比如，在上面這(zhè)個(gè)例子中，我們的(de)飲食觀測序列可(kě)以是 { 火鍋、拉面、拉面、火鍋、冰激淩、冰激淩、……、拉面、火鍋 }，另外我們知道天氣的(de)狀态有兩個(gè)。這(zhè)些信息便是我們所有的(de)輸入，機器學習(xí)将通(tōng)過它們訓練 HMM 模型。訓練 HMM 模型的(de)标準算(suàn)法是 Baum-Welch 算(suàn)法（又稱爲 forward-backward 算(suàn)法），它屬于一種最大(dà)期望算(suàn)法（Expectation-Maximization algorithm，EM 算(suàn)法）。它通(tōng)過叠代算(suàn)法，不斷的(de)改進對(duì) A 和(hé) B 的(de)估計，直到參數收斂。得(de)到 A 和(hé) B 之後，就可(kě)以用(yòng)它們計算(suàn)和(hé)回答(dá)有關狀态序列的(de)一系列問題。下(xià)面就來(lái)看一個(gè)量化(huà)投資領域的(de)例子。

5 HMM 在量化(huà)投資領域的(de)應用(yòng)

HMM 在量化(huà)投資中有哪些作用(yòng)呢(ne)？也(yě)許我們最關心的(de)問題是：它能否被用(yòng)來(lái)預測收益率或者價格呢(ne)？從馬爾可(kě)夫性質出發，我并不看好這(zhè)種可(kě)能性。雖然 HMM 的(de)無記憶性可(kě)以支持（弱）有效市場(chǎng)假說（即當前價格就包含了(le)對(duì)其未來(lái)做(zuò)預測所需的(de)全部信息），但種種經驗表明(míng)，弱有效市場(chǎng)假說并不成立。由于信息對(duì)不同投資者的(de)擴散速度不同，以及行爲金融學中的(de)反應過度和(hé)反應不足，價格或收益率的(de)曆史數據在預測未來(lái)時(shí)也(yě)能起到一定的(de)作用(yòng)。這(zhè)顯然與 HMM 的(de)無記憶性不符合。

舉例來(lái)說，如果已知今天上漲了(le) 1% 來(lái)預測明(míng)天的(de)收益率，我們仍然會看一看過去一段時(shí)間的(de)漲跌情況：連漲 3 天和(hé)連跌 5 天後發生的(de) 1% 的(de)上漲對(duì)投資者的(de)感受顯然是不同的(de)，收益率的(de)曆史軌迹将影(yǐng)響未來(lái)的(de)收益率。雖然也(yě)許無法直接預測收益率，但是 HMM 模型可(kě)以被用(yòng)來(lái)進行市場(chǎng)狀态監測（market regime detection）。每當新的(de)監管或政策的(de)出台，市場(chǎng)的(de)狀态可(kě)能發生系統性的(de)轉變。這(zhè)将對(duì)投資策略産生本質的(de)影(yǐng)響。從這(zhè)個(gè)意義上說，監測市場(chǎng)狀态十分(fēn)必要。由于市場(chǎng)的(de)“真實狀态”對(duì)于我們來(lái)說是未知的(de)——其實就連市場(chǎng)有幾個(gè)狀态都需要我們在建模中給定 —— 因此它是一個(gè)無監督學習(xí)問題。

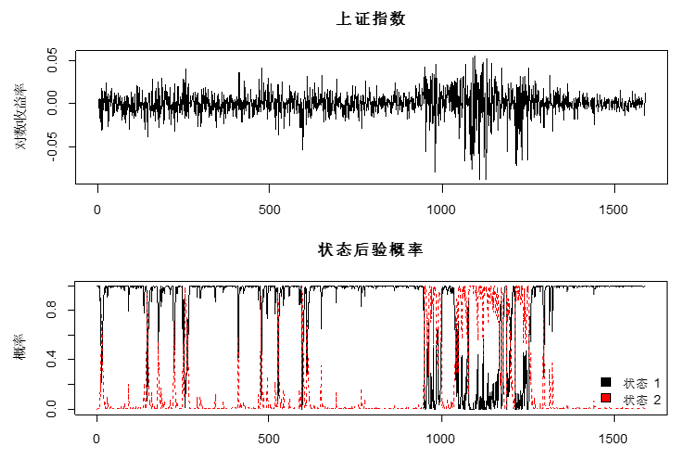
下(xià)面僅以一個(gè)非常簡單的(de)例子說明(míng) HMM 在這(zhè)方面的(de)應用(yòng)。假設市場(chǎng)有兩個(gè)狀态；觀測序列爲上證指數的(de)日對(duì)數收益率（觀測期爲 2011 年 1 月(yuè)到 2017 年 7 月(yuè)）。此外，我們需要指定發散概率分(fēn)布的(de)形态。由于對(duì)數收益率近似的(de)滿足正态分(fēn)布，因此我們假設在給定的(de)市場(chǎng)狀态下(xià)，觀測值滿足不同參數的(de)正态分(fēn)布（即它是連續的(de)分(fēn)布，這(zhè)與上面那個(gè)天氣和(hé)飲食例子中離散的(de)發散概率分(fēn)布不同）。我們希望通(tōng)過訓練 HMM 模型，根據收益率序列來(lái)估計 HMM 的(de)參數，并以此判斷每個(gè)交易日市場(chǎng)所處的(de)狀态。這(zhè)無疑屬于第三類問題。使用(yòng)最大(dà)期望算(suàn)法，得(de)到的(de)結果如下(xià)圖所示。

從圖中可(kě)以推測出 HMM 将市場(chǎng)劃分(fēn)爲平靜（狀态 1）和(hé)高(gāo)波動（狀态 2）兩個(gè)狀态。在 2014 年底之前，市場(chǎng)在絕大(dà)多(duō)數時(shí)間處于平靜狀态，但也(yě)不時(shí)出現高(gāo)波動狀态。在 2014 年底開始至 2016 年初結束的(de)牛熊周期中，市場(chǎng)處于高(gāo)波動狀态之中。自股災結束之後，市場(chǎng)則完全處于平靜狀态。雖然使用(yòng) HMM 直接預測收益率并不實際，但是對(duì)市場(chǎng)狀态的(de)正确判斷無疑對(duì)資産配置和(hé)風險控制至關重要。無獨有偶，從 2016 年第一季度開始，美(měi)股也(yě)進入了(le)“百年不遇”的(de)低波動周期，恐慌指數 VIX 屢創新低。在最近的(de)研究中，高(gāo)盛就對(duì)美(měi)股的(de)低波動性進行了(le)剖析。

無論我們多(duō)麽小心，低波動率都會在我們還(hái)沒有準備好時(shí)戛然停止；unknown unknowns 也(yě)一定會到來(lái)。想要應對(duì)這(zhè)些，首先必須對(duì)市場(chǎng)狀态有正确的(de)認知，這(zhè)便是 HMM 在量化(huà)投資領域的(de)價值之一。

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。