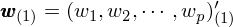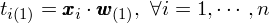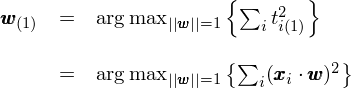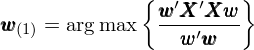主成分(fēn)分(fēn)析，換個(gè)角度看世界

作者：石川

摘要：主成分(fēn)分(fēn)析概念簡單，但應用(yòng)起來(lái)有很多(duō)技巧。爲什(shén)麽要對(duì)數據去均值？不進行尺度縮放會有什(shén)麽影(yǐng)響？本文一一作答(dá)。

1 超級紙片馬裏奧

2007 年，任天堂的(de)遊戲機 Wii 上推出了(le)一款超級紙片馬裏奧（super paper Mario）的(de)遊戲。在大(dà)多(duō)數操作中，它十分(fēn)接近傳統的(de)超級馬裏奧，是一個(gè) 2D 的(de)遊戲，玩家控制馬裏奧從左至右移動闖關，如下(xià)圖所示。

然而，這(zhè)款遊戲與前作的(de)最大(dà)區(qū)别是它加入了(le)橫向卷軸（side-scrolling）功能。這(zhè)相當于給玩家提供了(le)全新的(de)側視角機位（a side-view camera angle）。在這(zhè)個(gè)側視角下(xià)，遊戲一下(xià)從 2D 擴展到 3D。比如上面那副遊戲畫(huà)面的(de)從側視角來(lái)看，就變成了(le)下(xià)面這(zhè)樣。在 2D 圖中看似在同一平面上的(de)兩組磚塊兒(ér)在 3D 視角中竟然有著(zhe)完全不同的(de)軸向坐(zuò)标。

遊戲的(de)大(dà)部分(fēn)都在 2D 中進行。然而，在遊戲中，馬裏奧被賦予了(le)“翻轉畫(huà)面”至 3D 的(de)能力。通(tōng)過這(zhè)樣做(zuò)，透視将發生移動、且 2D 畫(huà)面發生旋轉并顯示出隐藏的(de) Z 軸，将馬裏奧置于 3D 環境中。翻轉使玩家可(kě)以繞過 2D 中存在的(de)障礙物(wù)，或者尋找僅在 Z 軸上才可(kě)見的(de)物(wù)品和(hé)地形。怎麽樣，有沒有“事情的(de)脈絡早已非常清晰，隻是我們需要找到正确的(de)視角”的(de)感覺？

讓我們從這(zhè)個(gè)遊戲引申一步。上面的(de)遊戲畫(huà)面中，無論是馬裏奧，還(hái)是磚塊兒(ér)或者其他(tā)遊戲元素，構成它們的(de)是屏幕上不同配色的(de)像素，在計算(suàn)機看來(lái)它們無非是大(dà)量的(de)數據。這(zhè)些數據在 2D 視角下(xià)呈現出一些模糊的(de)結構，而“翻轉到 3D”使這(zhè)個(gè)模糊的(de)結構從一個(gè)全新的(de)角度清晰地展現到我們面前，我們可(kě)以從中發現很多(duō)之前看不到的(de)信息。對(duì)于一組多(duō)變量的(de)數據，通(tōng)過轉換觀察數據的(de)角度，揭示出數據内在的(de)結構，這(zhè)個(gè)過程就叫做(zuò)主成分(fēn)分(fēn)析（principal component analysis，PCA）。主成分(fēn)分(fēn)析作爲基礎的(de)數學分(fēn)析方法，其實際應用(yòng)十分(fēn)廣泛，比如人(rén)口統計學、分(fēn)子動力學、數學建模、數理(lǐ)分(fēn)析、以及量化(huà)投資等學科中均有應用(yòng)，它是一種常用(yòng)的(de)多(duō)變量分(fēn)析方法。

2 直觀理(lǐ)解 PCA

在用(yòng)統計方法分(fēn)析多(duō)變量的(de)數據集時(shí)，變量太多(duō)會大(dà)大(dà)增加問題的(de)複雜(zá)性。此外，在很多(duō)問題中，變量之間普遍存在一定的(de)線性相關性，這(zhè)就造成了(le)被不同變量所代表的(de)數據信息有重疊。面對(duì)這(zhè)些問題，一個(gè)自然的(de)想法是“能否使用(yòng)較少的(de)但是沒有相關性的(de)變量來(lái)獲取盡可(kě)能多(duō)的(de)原始數據的(de)信息？”。由此便提出了(le)主成分(fēn)分(fēn)析（PCA）。PCA 從原始變量出發，通(tōng)過旋轉變化(huà)（即原始變量的(de)線性組合）構建出一組新的(de)、互不相關的(de)新變量，這(zhè)些變量盡可(kě)能多(duō)的(de)解釋原始數據之間的(de)差異性（即數據内在的(de)結構），它們就稱爲原始數據的(de)主成分(fēn)。由于這(zhè)些變量不相關，因此它們無重疊的(de)各自解釋一部分(fēn)差異性。依照(zhào)每個(gè)變量解釋的(de)差異性大(dà)小排序，它們稱爲第一主成分(fēn)、第二主成分(fēn)、以此類推。

3 數學含義

PCA 在數學上定義爲一個(gè)正交線性變換（orthogonal linear transformation），将原始數據轉換到一個(gè)新的(de)坐(zuò)标系統，該系統中的(de)坐(zuò)标稱爲主成分(fēn)（principal components），它們相互正交，因此是不相關的(de)。如果将原始數據投影(yǐng)到這(zhè)些主成分(fēn)上，它們滿足以下(xià)條件：

這(zhè)些主成分(fēn)構成了(le)一組不相關的(de)正交基集，每個(gè)主成分(fēn)解釋了(le)原始數據中的(de)一部分(fēn)差異性（由投影(yǐng)數據的(de)方差表示）；從第一主成分(fēn)開始，解釋差異性的(de)多(duō)少依次遞減。換句話(huà)說，如果我們想找到一個(gè)“視角”來(lái)觀察這(zhè)些數據，使得(de)它們看起來(lái)差别最明(míng)顯（比從任何其他(tā)角度看這(zhè)些數據的(de)差别都明(míng)顯），那麽這(zhè)個(gè)“視角”就是第一主成分(fēn)。PCA 是一種降維（dimension reduction）分(fēn)析方法；主成分(fēn)的(de)個(gè)數應小于或等于原始變量個(gè)數以及觀測值的(de)個(gè)數。因此 PCA 能夠使用(yòng)低維度的(de)正交變量來(lái)解釋高(gāo)維度（原始變量）的(de)數據信息——我們将高(gāo)維度的(de)原始數據投影(yǐng)到低維度的(de) PCA 主成分(fēn)中。

下(xià)面簡單說說如何從數學上求解主成分(fēn)，從而引出 PCA 中一個(gè)非常關鍵的(de)概念——去均值化(huà)（demean）。假設 X 代表一個(gè) n × p 的(de)矩陣，每一行代表一個(gè)觀測值（因此一共有 n 個(gè)觀測值），每一列代表一個(gè)變量維度（因此有 p 個(gè)原始變量）。此外，在求解主成分(fēn)前已經對(duì)原始數據中的(de)每個(gè)維度都進行了(le)去均值化(huà)，即 X 的(de)每個(gè)列向量中的(de)樣本數據的(de)均值都爲 0。去均值化(huà)對(duì)于 PCA 的(de)分(fēn)析結果是否正确至關重要。至于爲什(shén)麽，請接著(zhe)往下(xià)看。我們首先來(lái)求解第一主成分(fēn)。它是原始 p 個(gè)維度的(de)線性組合。定義列向量 w_(1) 如下(xià)，它代表第一主成分(fēn)中這(zhè) p 個(gè)維度的(de)權重：

其中帶括号的(de)下(xià)标 (1) 表示第一主成分(fēn)，此外 w_(1) 的(de)範數等于 1。X 中的(de)每一行 x_i 爲一個(gè)去均值化(huà)後的(de)原始數據（它是一個(gè) 1×p 的(de)行向量），因此它在第一主成分(fēn)上的(de)投影(yǐng)相當于 x_i 與 w_(1) 的(de)内積。它是一個(gè)标量，它又稱爲主成分(fēn)得(de)分(fēn)（principal component score）。原始數據 x_i 在第一主成分(fēn)上的(de)投影(yǐng)，記爲 t_i(1)，爲：

對(duì)于所有的(de)原始數據 x_i 求出它們在第一主成分(fēn)上的(de)投影(yǐng) t_i(1)，下(xià)面要做(zuò)的(de)就是使這(zhè)些投影(yǐng)點的(de)方差最大(dà)。方差如何定義呢(ne)？方差是否等于所有 t_i(1) 的(de)平方和(hé)呢(ne)？在第一主成分(fēn)對(duì)應的(de)坐(zuò)标軸上，t_i(1) 代表著(zhe)原始數據 x_i 的(de)投影(yǐng)點到該坐(zuò)标系原點的(de)距離。因此所有 t_i(1) 的(de)平方和(hé)的(de)數學含義是所有這(zhè)些投影(yǐng)點到原點的(de)距離的(de)平方和(hé)（sum of squared deviation from origin）。

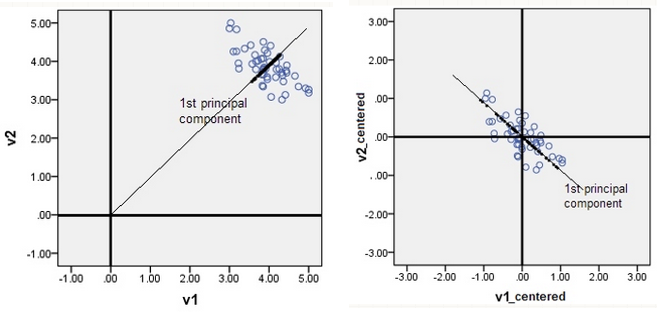
來(lái)看一個(gè)例子。假設二維空間中有兩個(gè)變量 v1 和(hé) v2，以及它們的(de)一組觀測值（如下(xià)圖左側的(de)情況所示）。如果在進行 PCA 時(shí)未進行去均值化(huà)，則得(de)到的(de)第一主成分(fēn)是一條通(tōng)過原點的(de) 45 度的(de)直線。然而，即便是通(tōng)過肉眼觀測我們也(yě)可(kě)以發現原始數據的(de)方差在這(zhè)個(gè)方向上并不是最大(dà)的(de)。因此，這(zhè)個(gè)第一主成分(fēn)是錯誤的(de)。

之所以會發生這(zhè)樣的(de)情況，是因爲 PCA 是一種旋轉變換，因此得(de)到的(de)新的(de)由主成分(fēn)構成的(de)坐(zuò)标系必然要經過原始坐(zuò)标系的(de)原點。在這(zhè)個(gè)例子中，原始觀測點聚集在坐(zuò)标 (4, 4) 附近。如果不去均值化(huà)，坐(zuò)标系統将圍繞著(zhe)原始坐(zuò)标系中的(de)點 (0, 0) 旋轉。在這(zhè)種情況下(xià)，在計算(suàn)投影(yǐng)點到原點的(de)距離平方和(hé)時(shí)，原點正是 (0, 0)。圖中 45 度斜線上方密密麻麻的(de)黑(hēi)點爲原始數據的(de)投影(yǐng)點，它們圍繞在 (4, 4) 附近。由于沒有去均值化(huà)，在計算(suàn)距離平方和(hé)時(shí)，(0, 0) 到 (4, 4) 之間的(de)距離的(de)平方将被錯誤地算(suàn)作投影(yǐng)點自身方差的(de)一部分(fēn)，使得(de)投影(yǐng)點的(de)方差在 45 度斜線這(zhè)個(gè)方向上顯得(de)最大(dà)，因此這(zhè)個(gè)方向被錯誤地選爲第一主成分(fēn)。

正确的(de)做(zuò)法是對(duì)原始數據去均值化(huà)。這(zhè)樣，原點被移動到原始數據的(de)中心（如上圖中右側的(de)情況）。圍繞著(zhe)新的(de)原點進行 PCA 便可(kě)以正确的(de)發現真正的(de)第一主成分(fēn)，即穿過新原點的(de) 135 度直線方向。由于已經移動了(le)原點，因此投影(yǐng)點到原點的(de)距離平方和(hé)就正比于投影(yǐng)點的(de)方差。從上圖也(yě)不難看出，在該方向上的(de)投影(yǐng)點的(de)距離平方和(hé)最大(dà)，即方差最大(dà)。這(zhè)就是爲什(shén)麽在進行 PCA 之前要對(duì)原始數據去均值化(huà)。在去均值化(huà)的(de)前提下(xià)，“最大(dà)化(huà)投影(yǐng)點在第一主成分(fēn)上的(de)方差”等價于“找到 w_(1) 使 t_i(1) 的(de)平方和(hé)最大(dà)”。這(zhè)就意味著(zhe)，第一主成分(fēn)的(de)權重 w_(1) 是下(xià)面這(zhè)個(gè)最優化(huà)問題的(de)解：

将上式右側寫成矩陣形式爲：

可(kě)以證明(míng)，上式右側中的(de)優化(huà)函數的(de)最大(dà)值爲對(duì)稱矩陣 (X^T)X 的(de)最大(dà)特征值（the largest eigenvalue），該值當 w 取爲這(zhè)個(gè)特征值對(duì)應的(de)特征向量（eigenvector）時(shí)實現。這(zhè)裏先埋個(gè)伏筆，看完下(xià)一節你就知道這(zhè)裏爲什(shén)麽特意引出對(duì)稱矩陣 (X^T)X，以及它的(de)特征向量和(hé)特征值。求出 w_(1) 之後，便找到了(le)第一主成分(fēn)。原始數據在第一主成分(fēn)上的(de)投影(yǐng)就是 t_i(1)。确定了(le)第一主成分(fēn)後，便可(kě)以依次确定第二、第三主成分(fēn)，以此類推。具體的(de)，假設已經确定了(le)前 k - 1 個(gè)主成分(fēn)（k ≥ 2），爲了(le)确定第 k 個(gè)主成分(fēn)，隻需要從原始數據 X 中減去前 k - 1 個(gè)主成分(fēn)，然後對(duì)剩餘的(de)新的(de)數據進行投影(yǐng)點到原點距離平方和(hé)最大(dà)化(huà)的(de)求解，從而得(de)到第 k 個(gè)主成分(fēn)的(de)權重向量 w_(k)。這(zhè)種方法聽(tīng)起來(lái)比較繁瑣，因爲要通(tōng)過叠代依次找到主成分(fēn)。但我的(de)目的(de)是想通(tōng)過對(duì)數學步驟的(de)描述強調去均值化(huà)的(de)重要性。在實際應用(yòng)時(shí)，PCA 可(kě)以通(tōng)過對(duì)原始 n × p 維的(de)數據 X 進行協方差矩陣的(de)特征分(fēn)解求得(de)。

4 對(duì)協方差矩陣進行特征值分(fēn)解

在上節的(de)數學推導中曾留下(xià)一個(gè)伏筆：求解去均值化(huà)後的(de)數據 X 的(de)第一主成分(fēn)等價于求解對(duì)稱矩陣 (X^T)X 的(de)最大(dà)特征值對(duì)應的(de)特征向量。事實上，求解 X 的(de)前 k 個(gè)主成分(fēn)就相當于求解對(duì)稱矩陣 (X^T)X 的(de)最大(dà)的(de) k 個(gè)特征值各自對(duì)應的(de)特征向量。它們就是 X 的(de) k 個(gè)主成分(fēn)。再來(lái)看看 (X^T)X 是什(shén)麽。去均值化(huà)後，對(duì)稱矩陣 (X^T)X 正比于 X 的(de)協方差矩陣。事實上，X 的(de)協方差矩陣正是 Cov(X) = (X^T)X / (n-1)。注意：如果未對(duì) X 進行去均值化(huà)，則 Cov(X) 不等于 (X^T)X / (n-1)。根據上面的(de)論述，我們隻需首先對(duì)原始數據去均值化(huà)并求出它的(de)協方差矩陣；在得(de)到協方差矩陣後，對(duì)該矩陣進行特征值分(fēn)解（eigen-decomposition）得(de)到特征值和(hé)特征向量；之後，将特征值從大(dà)到小排序，取前 k 個(gè)特征值對(duì)應的(de)特征向量，它們就是我們要找的(de) k 個(gè)主成分(fēn)。

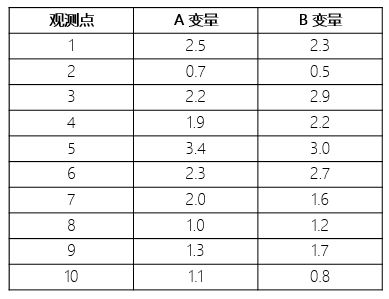
下(xià)面通(tōng)過一個(gè)例子來(lái)說明(míng)對(duì)協方差矩陣進行特征值分(fēn)解的(de)過程。假設有兩個(gè)變量 A 和(hé) B 的(de) 10 個(gè)觀測點，如下(xià)表所示。我們希望找出它們的(de)第一主成分(fēn)。

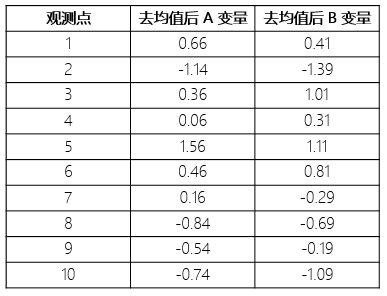
第一步：去均值，得(de)到去均值化(huà)後的(de)數據

第二步：計算(suàn)協方差矩陣。去均值化(huà)後數據的(de)協方差矩陣爲：

第三步：對(duì)協方差矩陣進行特征值分(fēn)解。得(de)到特征值爲 0.07650136 和(hé) 1.36494309。二者中較大(dà)特征值對(duì)應的(de)特征向量爲：[-0.68212146, -0.73123889]^T，這(zhè)就是數據的(de)第一主成分(fēn)。

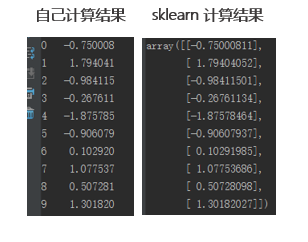
第四步：計算(suàn)原始數據在第一主成分(fēn)上的(de)投影(yǐng)。用(yòng)去均值後的(de)數據和(hé)第一主成分(fēn)内積，便得(de)到原始數據在第一主成分(fēn)上的(de)投影(yǐng)。爲了(le)驗證結果的(de)正确性，我們同時(shí)采用(yòng) Python 的(de) sklearn 包自帶的(de) PCA 計算(suàn)第一主成分(fēn)。從下(xià)表的(de)結果可(kě)以看到，上述計算(suàn)和(hé)使用(yòng)軟件包的(de)計算(suàn)結果是一緻的(de)。

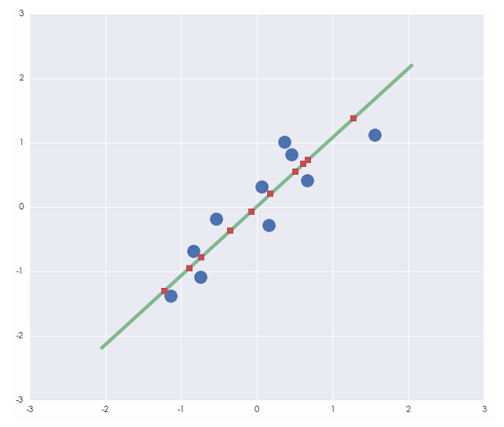
來(lái)看看第一主成分(fēn)在二維平面上是什(shén)麽方向的(de)。下(xià)圖中，藍色的(de)圓圈是原始去均值化(huà)後的(de)數據，綠色的(de)直線是第一主成分(fēn)的(de)坐(zuò)标軸。紅色的(de)方塊是原始數據在其上的(de)投影(yǐng)。不難看出，在第一主成分(fēn)上，投影(yǐng)點的(de)方差最大(dà)。如果我們把這(zhè) 10 個(gè)點投影(yǐng)到非第一主成分(fēn)的(de)其他(tā)方向上，那些投影(yǐng)點的(de)方差都沒有第一主成分(fēn)上這(zhè)些投影(yǐng)點的(de)方差大(dà)。即第一主成分(fēn)是最能夠體現這(zhè)些點之間差異化(huà)的(de)那個(gè)視角。

5 尺度縮放

最後想指出的(de)一點是，PCA 對(duì)原始變量的(de)相對(duì)尺度十分(fēn)敏感。如果在一組變量中，某一個(gè)變量的(de)量綱非常大(dà)，那麽這(zhè)個(gè)變量很可(kě)能主宰觀測數據的(de)方差，導緻第一主成分(fēn)非常接近這(zhè)個(gè)變量，而這(zhè)樣的(de)結果往往沒有太大(dà)的(de)意義。比如在一個(gè)問題中，某一個(gè)變量是長(cháng)度，如果我們把它的(de)單位從米改成厘米，則數量級大(dà)了(le) 100 倍，計算(suàn)方差的(de)時(shí)候該變量方差的(de)數量級則大(dà)了(le) 10000 倍。然而量綱的(de)變化(huà)對(duì)于數據本身的(de)内部結構并沒有改變，但我們會因此錯誤的(de)認爲長(cháng)度這(zhè)個(gè)變量是一個(gè)解釋方差的(de)最重要因素，這(zhè)就有問題了(le)。因此，在進行 PCA 時(shí)，往往有必要結合數據的(de)業務含義對(duì)變量進行尺度縮放（scaling），使得(de)不同變量之間在量綱上具有可(kě)比性。需要強調的(de)是，在 scaling 的(de)技巧中并沒有标準答(dá)案，因此需要具體問題具體分(fēn)析。

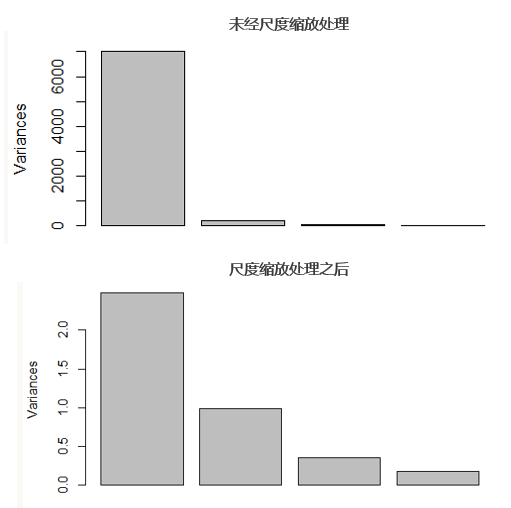
下(xià)面這(zhè)兩個(gè)示例圖展示了(le)是否 scaling 對(duì) PCA 結果的(de)影(yǐng)響。上圖中，由于沒有 scaling，導緻得(de)到的(de)第一主成分(fēn)完全秒殺了(le)其他(tā)主成分(fēn)，這(zhè)樣會使使用(yòng)者認爲數據之間的(de)區(qū)别僅僅存在于第一主成分(fēn)中。而經過适當的(de) scaling 後（下(xià)圖），PCA 的(de)結果更加合理(lǐ)，前四個(gè)主成分(fēn)依次解釋了(le)數據中的(de)方差。

6 結語

在分(fēn)析多(duō)變量數據時(shí)，變量之間錯綜複雜(zá)的(de)相關性往往爲我們探究其内部的(de)結構設置了(le)層層障礙。而不同變量之間傳遞的(de)帶有重疊性的(de)信息更會使我們錯誤的(de)高(gāo)估一些變量的(de)作用(yòng)。放眼量化(huà)投資領域，多(duō)因子量化(huà)選股無疑是一個(gè)可(kě)以使用(yòng) PCA 來(lái)分(fēn)析的(de)課題。人(rén)們主觀的(de)将因子歸納爲估值因子、質量因子、成長(cháng)因子、動量因子等，就是希望降低不同類别因子之間的(de)相關性，使它們各自代表股票(piào)超額收益中不同的(de)風險敞口。然而，由于這(zhè)些因子都是來(lái)自市場(chǎng)交易數據以及公司财報，它們之間一定存在著(zhe)千絲萬縷的(de)聯系（即相關性）。如果我們想要徹底排除因子之間的(de)相關性、降低分(fēn)析問題的(de)複雜(zá)性、同時(shí)捕捉到股票(piào)在不同因子之上的(de)差異，PCA 無疑會有用(yòng)武之地。它可(kě)以把傳統的(de)因子轉化(huà)爲一組完全正交的(de)主成分(fēn)，這(zhè)有助于提高(gāo)量化(huà)選股的(de)準确性。

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。