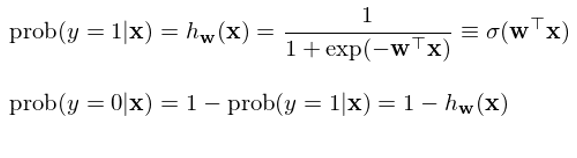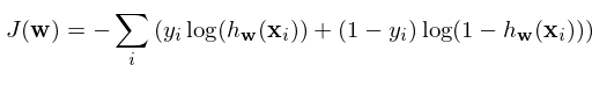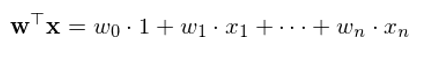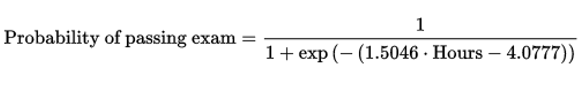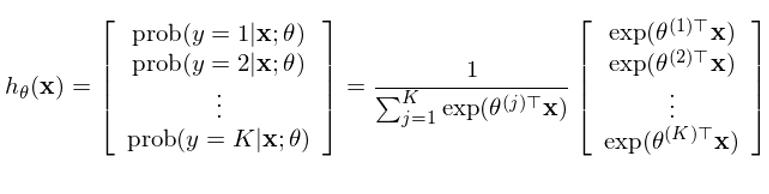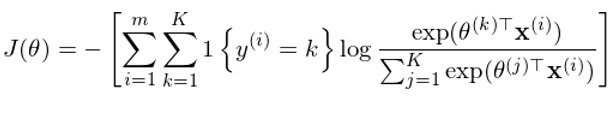邏輯回歸，很有邏輯

作者：石川

摘要：摘要：邏輯回歸是一種有機監督學習(xí)分(fēn)類器，在量化(huà)投資領域可(kě)以被用(yòng)來(lái)選股。本文介紹邏輯回歸的(de)數學背景和(hé)應用(yòng)實踐。

1 邏輯回歸分(fēn)類器

邏輯回歸由統計學家 David Cox 于 1958 年提出。與傳統的(de)線性回歸不同，邏輯回歸（logistic regression）中響應變量（因變量）的(de)取值不是連續的(de)，而是離散的(de)，每個(gè)取值代表一個(gè)不同的(de)類别。因此，邏輯回歸的(de)本質是一個(gè)分(fēn)類器（classifier）。它是一種有監督學習(xí)，通(tōng)過訓練集數據中的(de)樣本的(de)特征向量 x 和(hé)标簽 y（即響應變量的(de)類别）來(lái)訓練模型的(de)參數，并使用(yòng)該模型對(duì)未來(lái)的(de)新樣本進行分(fēn)類。

最簡單的(de)邏輯回歸中響應變量是二分(fēn)類的(de)（binary），即它僅僅可(kě)以取兩個(gè)值，代表不同的(de)兩類。按照(zhào)慣例，它的(de)取值爲 0 和(hé) 1。即便是最簡單的(de)模型也(yě)有廣泛的(de)應用(yòng)，比如這(zhè)兩類可(kě)以代表著(zhe)比賽中的(de)輸和(hé)赢、考試中的(de)通(tōng)過和(hé)失敗、醫療領域的(de)健康和(hé)生病、以及股市中的(de)漲和(hé)跌等。如果響應變量的(de)取值多(duō)于兩類，則這(zhè)樣的(de)問題叫做(zuò)多(duō)項邏輯回歸（multinomial logistic regression）。

本文以最簡單的(de)二元邏輯模型（binary logistic model，即響應變量 y 隻能取 0 和(hé) 1 兩個(gè)值）爲例，介紹邏輯回歸的(de)數學含義以及它在量化(huà)選股中的(de)應用(yòng)。本文的(de)最後會簡單談一談求解多(duō)項邏輯回歸——即 Softmax 回歸——以及它在卷積神經網絡中的(de)應用(yòng)。下(xià)文中如無特殊說明(míng)，當我們提到“邏輯回歸”時(shí)，指代的(de)都是最簡單的(de)二元邏輯回歸。

2 數學模型

在二元邏輯回歸中，回歸模型根據樣本點的(de)特征（features）計算(suàn)該樣本點屬于每一類的(de)條件概率。在數學上，通(tōng)過給定的(de)函數将樣本點的(de) n 維特征向量 x 轉化(huà)成一個(gè)概率标量。具體的(de)，具備特征向量 x 的(de)樣本點屬于 1 和(hé) 0 兩類的(de)條件概率爲：

其中，函數 σ(z) ≡ 1 / (1 + exp(-z)) 被稱爲邏輯函數（logistic function）或 sigmoid 函數（因爲 σ(z) 形如 S 曲線）；它的(de)取值範圍在 0 和(hé) 1 之間。邏輯回歸的(de)目的(de)是通(tōng)過訓練集數據找到最優的(de)權重 w 使得(de)分(fēn)類結果盡量同時(shí)滿足如下(xià)目标：

邏輯回歸将樣本點的(de)特征向量 x 按照(zhào)權重 w 進行線性組合得(de)到标量 z，再将 z 放入邏輯函數 σ(z) 最終求出該樣本點屬于類别 1 以及 0 的(de)概率，從而對(duì)其進行分(fēn)類——如果 h_w(x) > 1 - h_w(x) 則該樣本點被分(fēn)爲類别 1，反之爲類别 0。

如何決定權重 w 呢(ne)？假設訓練集共有 m 對(duì)兒(ér)數據 {(x_i, y_i), i = 1, 2, …, m}，爲了(le)盡量同時(shí)實現上述目标，定義 cost function 如下(xià)：

使用(yòng)訓練集數據訓練模型的(de)參數 w 以使上述 cost function 最小化(huà)。對(duì)于訓練集中的(de)每一個(gè)樣本點，上述方程的(de)兩項中有且僅有一個(gè)不爲 0。對(duì)于第 i 個(gè)樣本點，如果 y_i = 1，則最小化(huà)上述方程意味著(zhe)最大(dà)化(huà) h_w(x_i)，即最大(dà)化(huà)該點被分(fēn)類爲 1 的(de)概率；同理(lǐ)，如果 y_i = 0，則最小化(huà)上述方程意味著(zhe)最大(dà)化(huà) 1 - h_w(x_i)，即最大(dà)化(huà)該點被分(fēn)類爲 0 的(de)概率。

從上面的(de)論述可(kě)知，J(w) 同時(shí)考慮了(le) 1 和(hé) 0 兩類分(fēn)類的(de)準确性。使用(yòng)訓練集對(duì)該模型訓練，找到最優的(de) w，使得(de) J(w) 最小，這(zhè)就是邏輯回歸模型的(de)學習(xí)過程。一旦确定了(le)模型參數，就可(kě)以使用(yòng)它對(duì)新的(de)樣本進行分(fēn)類。對(duì)于新的(de)樣本點特征向量 x'，如果 h_w(x') > 0.5，則該點被分(fēn)到 y = 1 類；反之被分(fēn)到 y = 0 類。最優化(huà) J(w) 可(kě)以采用(yòng)梯度搜索（gradient search），爲此隻需要計算(suàn)出 J 的(de)梯度 ∇J(w)，在此不再贅述。

最後值得(de)一提的(de)是，在計算(suàn)特征向量的(de)線性組合時(shí)，往往會額外考慮一個(gè)截距項。這(zhè)相當于在原始 n 維特征向量 x 中加入一個(gè)元素 1（因此特征向量變爲 n+1 維），而x的(de)線性組合也(yě)因此變爲：

當然，這(zhè)個(gè)截距項不是必須的(de)。使用(yòng)者可(kě)以根據待解決的(de)問題判斷是否應該在特征向量中加入該項。流行的(de)統計分(fēn)析工具（比如 Python 的(de) sklearn）允許使用(yòng)者自行決定是否在模型中加入截距項。

3 一個(gè)例子

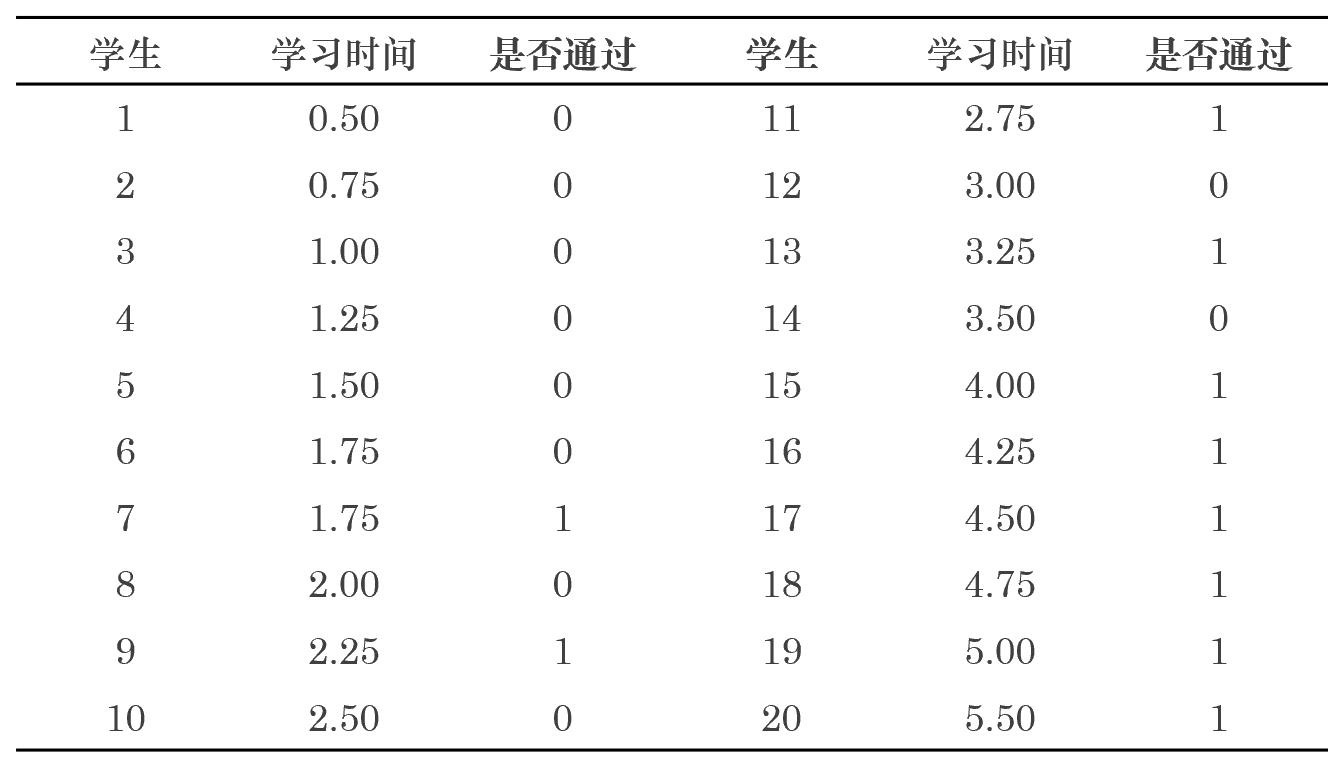
讓我借用(yòng) Wikipedia 上面的(de)例子來(lái)說明(míng)邏輯回歸的(de)應用(yòng)。這(zhè)是一個(gè)關于學習(xí)時(shí)間和(hé)考試通(tōng)過與否的(de)例子。假設一共有 20 名學生（樣本點），特征向量爲截距項 1 和(hé)學習(xí)時(shí)間組成的(de)二維向量。考試結果分(fēn)爲 1（通(tōng)過）和(hé) 0（失敗）。我們采用(yòng)邏輯回歸來(lái)建立考試時(shí)間和(hé)通(tōng)過與否之間的(de)關聯。訓練集數據如下(xià)：

使用(yòng)訓練集數據建模，得(de)到的(de)邏輯回歸模型參數（特征向量的(de)權重）：

從模型參數可(kě)以看出，是否通(tōng)過考試和(hé)該學生的(de)努力程度（學習(xí)時(shí)間）是正相關的(de)，這(zhè)符合人(rén)們的(de)預期。将模型參數帶入到 sigmoid 函數中便可(kě)計算(suàn)出給定學習(xí)時(shí)間下(xià)考試通(tōng)過的(de)概率：

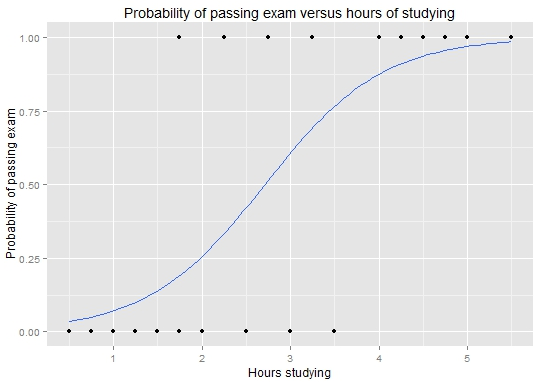
使用(yòng)該模型便可(kě)以對(duì)新的(de)考生是否通(tōng)過考試進行判斷。将訓練集中的(de) 20 名考生的(de)學習(xí)時(shí)間帶入到上式可(kě)繪制圖這(zhè)個(gè) sigmoid 函數（确實形如 S 曲線）：

4 使用(yòng)邏輯回歸選股

經過上面的(de)介紹，我們已經對(duì)邏輯回歸的(de)原理(lǐ)和(hé)它的(de)應用(yòng)有了(le)一定的(de)認識。下(xià)面就來(lái)将它應用(yòng)于量化(huà)投資相關的(de)領域——選股。爲說明(míng)這(zhè)一點，使用(yòng)股票(piào)的(de)因子作爲特征向量，使用(yòng)股票(piào)的(de)漲跌強弱作爲響應變量，建立邏輯回歸模型來(lái)選股。本實驗中，以中證 500 的(de)成分(fēn)股爲例。特别的(de)，考慮 2016 年 12 月(yuè) 31 日時(shí)這(zhè) 500 支成分(fēn)股的(de)最新截面因子數據。考察的(de)十個(gè)因子包括：EP、BP、ROE、Liability/Asset、規模、換手率、動量、反轉、市場(chǎng) β、殘差波動率。

由于選股的(de)目的(de)是使用(yòng)因子來(lái)對(duì)未來(lái)的(de)收益率做(zuò)預測，因此我們使用(yòng)這(zhè) 500 支成分(fēn)股在 2017 年 1 月(yuè)份的(de)收益率作爲響應變量的(de)原始數據。由于在二元邏輯回歸中，響應變量必須是二元的(de)，因此我們需要将這(zhè) 500 支個(gè)股的(de)絕對(duì)收益率轉換成 0 和(hé) 1。爲此，可(kě)以有以下(xià)幾種方法：

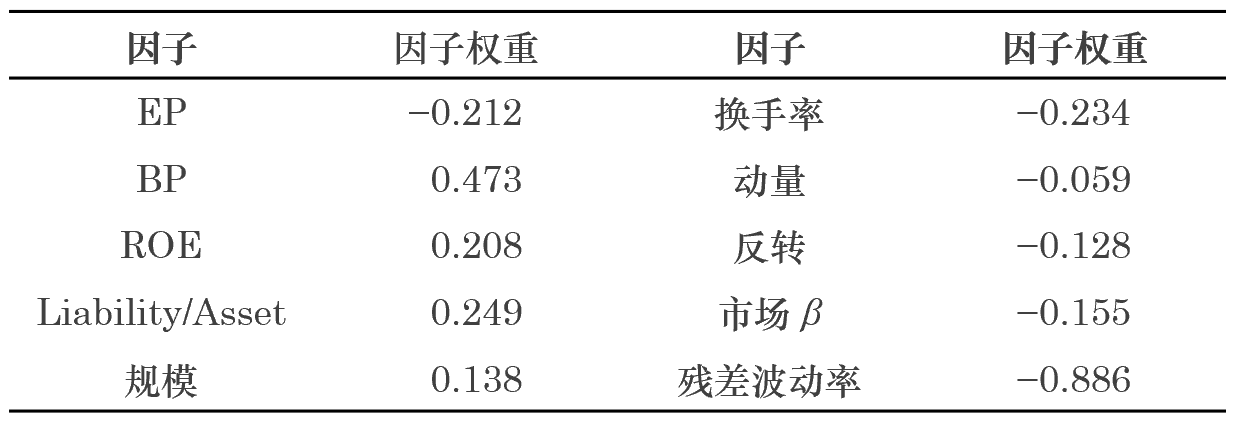
在量化(huà)選股中，爲了(le)對(duì)沖掉市場(chǎng)風險，往往希望判斷股票(piào)的(de)相對(duì)強弱。實驗中采用(yòng)上述的(de)第三種方法将股票(piào)的(de)收益率轉化(huà)爲二元響應變量。訓練集數據準備就緒，便可(kě)以訓練回歸模型。假設特征向量中不考慮截距項，得(de)到的(de)回歸模型參數如下(xià)。

可(kě)以看出，收益率和(hé) BP 以及 ROE 成正比。有意思的(de)是，收益率和(hé) β 成反比。這(zhè)似乎說明(míng)市場(chǎng)更加青睐小 β 的(de)藍籌股。想更系統的(de)分(fēn)析每個(gè)因子對(duì)于選股的(de)作用(yòng)，需要使用(yòng)多(duō)期數據同時(shí)在時(shí)間和(hé)截面兩個(gè)維度進行邏輯回歸。接下(xià)來(lái)看看在這(zhè)個(gè)簡單的(de)實驗中，邏輯回歸模型對(duì)樣本内數據的(de)分(fēn)類正确性。預測的(de)正确性必須從準确率和(hé)召回率兩方面同時(shí)評價。假設我們預測一共有 X 支股票(piào)上漲，其中有 A 支猜對(duì)了(le)、B 支猜錯了(le)；我們預測一共有 Y = (500 - X) 支下(xià)跌，其中有 C 支猜錯了(le)、D 支猜對(duì)了(le)。則這(zhè)兩個(gè)指标的(de)定義爲：

準确率衡量的(de)是在所有你猜測的(de)某一類（漲或跌）樣本中，有多(duō)少是正确的(de)；而召回率是用(yòng)來(lái)衡量在所有某一類的(de)（漲或跌）樣本中，有多(duō)少被你猜出來(lái)了(le)。對(duì)于實驗中的(de)這(zhè)個(gè)邏輯回歸模型，它的(de)正确性如下(xià)：

僅從這(zhè)些數字上來(lái)看，似乎效果還(hái)不錯。但是不要忘記，這(zhè)僅僅是對(duì)樣本内數據的(de)判斷結果（模型就是用(yòng)它們來(lái)構建的(de)）；這(zhè)些不說明(míng)樣本外的(de)預測準确性。通(tōng)過這(zhè)個(gè)例子，僅僅想說明(míng)利用(yòng)邏輯回歸可(kě)以進行量化(huà)選股。因此，我們的(de)例子止于此。在真正應用(yòng)中，正如前文提到的(de)，應該使用(yòng)多(duō)期在時(shí)間和(hé)截面兩個(gè)維度的(de)樣本數據建模，并采用(yòng)交叉驗證來(lái)評價模型在樣本外的(de)分(fēn)類準确性，以此最終确定模型的(de)參數。

5 邏輯回歸、Softmax 回歸和(hé)卷積神經網絡

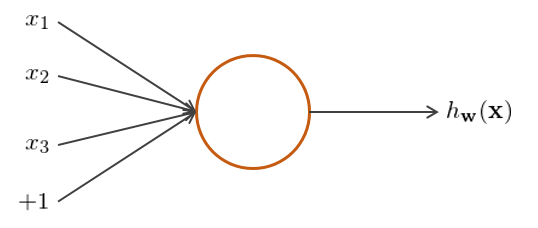
最後，簡單談談邏輯回歸、Softmax 回歸和(hé)卷積神經網絡的(de)關系。先來(lái)說說神經網絡（neural networks），它由多(duō)個(gè)、多(duō)層神經元（neuron）構成，每個(gè)神經元就是一個(gè)計算(suàn)單元（見下(xià)圖），由輸入特征、輸出值、以及激活函數構成。

在這(zhè)個(gè)例子中，x_1、x_2、x_3 和(hé)截距項 1 就是輸入的(de)特征，h_w(x) 就是輸出，而邏輯回歸中的(de) sigmoid 函數就是一種常見的(de)激活函數（其他(tā)常見的(de)激活函數包括 tanh 函數和(hé) max 函數等）。

再來(lái)看看 Softmax 回歸。它是一種多(duō)項邏輯回歸，即響應變量的(de)取值大(dà)于兩類。假設共有 K > 2 類，每個(gè)樣本點的(de)響應變量 y_i 的(de)取值爲 1 到 K 之間的(de)某一個(gè)值。多(duō)項邏輯回歸的(de)應用(yòng)更加廣泛，比如在手寫數字識别中，一共有 0 到 9 是個(gè)數字，因此一共可(kě)以有 10 類。将二元邏輯回歸的(de)數學含義延伸易知，在 Softmax 回歸中我們希望計算(suàn)出樣本點在其給定的(de)特征向量下(xià)，屬于每一類的(de)條件概率：

其中 θ^(1)，θ^(2)，……，θ^(K) 爲模型的(de)參數，通(tōng)過訓練集數據訓練得(de)到。與二元邏輯回歸類似，定義 cost function 如下(xià)：

其中 1{} 爲指示函數，當 {} 中的(de)條件爲真時(shí)，它的(de)取值爲 1，否則爲 0。通(tōng)過最小化(huà)這(zhè)個(gè)目标函數就可(kě)以得(de)到最優的(de)參數 θ^(1)，θ^(2)，……，θ^(K)。求解時(shí)同樣可(kě)以采用(yòng)梯度搜索法。

Softmax 回歸往往作爲卷積神經網絡（Convolutional Neural Network）的(de)最後一步。卷積神經網絡是在神經網絡上發展出來(lái)的(de)，可(kě)以被用(yòng)來(lái)進行圖像識别的(de)強大(dà)工具。傳統神經網絡在面對(duì)高(gāo)像素的(de)圖像進行識别時(shí)無能爲力，這(zhè)是因爲高(gāo)像素對(duì)應的(de)特征數巨大(dà)，遠(yuǎn)超過計算(suàn)機可(kě)以承受的(de)範圍；此外巨大(dà)的(de)特征也(yě)使得(de)特征矩陣非常稀疏。卷積神經網絡通(tōng)過卷積計算(suàn)對(duì)原始的(de)特征進行高(gāo)度的(de)抽象，通(tōng)過局部感知和(hé)參數共享大(dà)大(dà)的(de)減少了(le)特征數。此外，它通(tōng)過使用(yòng)多(duō)層卷積以及池化(huà)等手段，進一步抽象特征，最終得(de)到原始圖像的(de)高(gāo)度提煉的(de)信息。而在最後一步，使用(yòng)這(zhè)個(gè)高(gāo)度抽象的(de)信息對(duì)圖像進行分(fēn)類（識别），計算(suàn)它屬于不同類别的(de)概率。在實際應用(yòng)中，圖像的(de)類别往往成百上千，甚至更多(duō)，這(zhè)便要用(yòng)到 Softmax 回歸。

參考文獻

https://en.wikipedia.org/wiki/Logistic_regression

http://ufldl.stanford.edu/tutorial/supervised/SoftmaxRegression/

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。