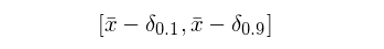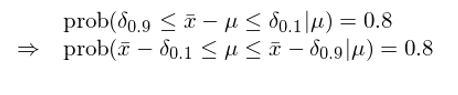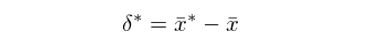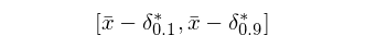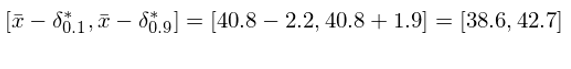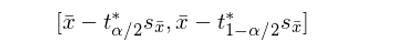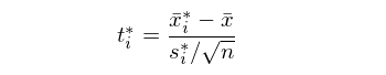用(yòng) Bootstrap 進行參數估計大(dà)有可(kě)爲

作者：石川

摘要：本文介紹如何使用(yòng) Bootstrap 進行參數估計。該方法對(duì)總體分(fēn)布不做(zuò)假設，可(kě)以用(yòng)于各種統計量，十分(fēn)強大(dà)。

1 從 t 分(fēn)布說起

在量化(huà)投資領域，有大(dà)量需要進行參數估計（parameter estimation）的(de)場(chǎng)景。比如在按照(zhào)馬科維茨的(de)均值方差框架配置資産時(shí)，就必須計算(suàn)投資品的(de)收益率均值和(hé)協方差矩陣。很多(duō)時(shí)候，對(duì)于需要的(de)統計量，僅有點估計（point estimate）是不夠的(de)，我們更感興趣的(de)是從樣本數據得(de)到的(de)點估計和(hé)該統計量在未知總體中的(de)真實值之間的(de)誤差。在這(zhè)方面，區(qū)間估計 —— 即計算(suàn)出目标統計量的(de)置信區(qū)間（confidence interval）—— 可(kě)以提供我們需要的(de)信息。

談到置信區(qū)間，人(rén)們最熟悉的(de)當屬計算(suàn)總體均值（population mean）的(de)置信區(qū)間。這(zhè)是因爲在中心極限定理(lǐ)（Central Limit Theorem）和(hé)正态分(fēn)布假設（Normal distribution）下(xià)，總體均值的(de)置信區(qū)間存在一個(gè)優雅的(de)解析表達。利用(yòng)樣本均值和(hé)其 standard error 計算(suàn)出的(de) test statistic 滿足 t 分(fēn)布（Student's t-distribution），通(tōng)過查表找到置信區(qū)間兩邊各自對(duì)應的(de) t 統計量的(de)臨界值（critical value）便可(kě)以方便的(de)求出置信區(qū)間。由于 t 分(fēn)布是對(duì)稱的(de)，因此總體均值的(de)置信區(qū)間是關于樣本均值對(duì)稱的(de)。

讓我們稱上述計算(suàn)置信區(qū)間的(de)方法爲傳統的(de) Normal Theory 方法。我想花點時(shí)間來(lái)聊聊該方法背後的(de)兩個(gè)強大(dà)假設：中心極限定理(lǐ)和(hé)正态分(fēn)布。假設總體滿足正态分(fēn)布，而我們想計算(suàn)均值的(de)置信區(qū)間。如果總體的(de)标準差 σ 已知，則可(kě)以使用(yòng)正态分(fēn)布計算(suàn)均值的(de)置信區(qū)間；如果 σ 未知，則使用(yòng)樣本的(de)标準差 s 代替，并且利用(yòng) t 分(fēn)布來(lái)代替正态分(fēn)布計算(suàn)均值的(de)計算(suàn)區(qū)間。這(zhè)就是 t 分(fēn)布被提出來(lái)的(de)初衷。因此，使用(yòng) t 分(fēn)布計算(suàn)均值的(de)置信區(qū)間隐含著(zhe)總體分(fēn)布滿足正态分(fēn)布這(zhè)個(gè)假設。但是，對(duì)于實際中的(de)問題，總體并不滿足正态分(fēn)布，因此看起來(lái)我們不能使用(yòng) t 分(fēn)布計算(suàn)均值的(de)置信區(qū)間。好消息是，我們還(hái)有另外一個(gè)“大(dà)招”：中心極限定理(lǐ)。中心極限定理(lǐ)告訴我們，不管總體的(de)分(fēn)布是什(shén)麽樣，總體的(de)均值近似滿足正态分(fēn)布，因此我們仍然可(kě)以使用(yòng) t 分(fēn)布計算(suàn)置信區(qū)間。

可(kě)見，對(duì)于一個(gè)未知分(fēn)布總體均值的(de)推斷，我們必須倚賴中心極限定理(lǐ)和(hé)正态分(fēn)布的(de)假設。如果未知分(fēn)布非常不規則或樣本數不足，則中心極限定理(lǐ)指出的(de)均值近似爲正态分(fēn)布便難以成立，而基于 t 分(fēn)布計算(suàn)出來(lái)的(de)均值置信區(qū)間也(yě)不夠準确。除了(le)均值外，對(duì)于人(rén)們關心的(de)許多(duō)其他(tā)統計量，比如中位數、分(fēn)位數、标準差、或者相關系數，它們與均值不同，無法從 Normal Theory 中可(kě)以得(de)到優雅的(de)解析表達式來(lái)計算(suàn)其置信區(qū)間，因此上述傳統方法無能爲力。從上面的(de)分(fēn)析可(kě)知，僅僅掌握傳統的(de) Normal Theory 方法局限性很大(dà)，使得(de)我們在求解置信區(qū)間的(de)很多(duō)問題面前舉步維艱。因此，今天就給大(dà)家介紹一個(gè)利器 —— Bootstrap 方法。它在計算(suàn)統計量的(de)置信區(qū)間時(shí)大(dà)有可(kě)爲。

2 Bootstrap 方法

The bootstrap is a computer-based method for assigning measures of accuracy to statistical estimates. -- Efron & Tibshirani, An introduction to the bootstrap, 1993

自 1979 年以來(lái)，Bootstrap 方法得(de)到了(le)廣泛的(de)推廣，其始作俑者是 Bradley Efron （Bootstrap 這(zhè)個(gè)詞也(yě)是他(tā)發明(míng)的(de)）。它的(de)核心思想是通(tōng)過使用(yòng)數據本身，從而估計從該數據中計算(suàn)出來(lái)的(de)統計數據的(de)變化(huà)。現代計算(suàn)機強大(dà)的(de)計算(suàn)能力使得(de)該方法的(de)實現非常簡單。Bootstrap 一詞出自英文習(xí)語“pull yourself up by your bootstraps”，它的(de)直譯是“通(tōng)過拉你自己靴子的(de)鞋帶把你自己從地面上拉起來(lái)”。它的(de)隐含意是“improve your situation by your own efforts”，即“通(tōng)過你自己的(de)努力（而非他(tā)人(rén)幫助）來(lái)解決困難改善處境”。因此，Bootstrap 一詞就代表了(le)“自力更生”。放到參數估計的(de)上下(xià)文中，Bootstrap 意味著(zhe)我們僅僅通(tōng)過使用(yòng)手頭上的(de)樣本數據（樣本數據“自力更生”）而不對(duì)總體的(de)分(fēn)布做(zuò)任何假設（比如傳統方法中的(de)正态分(fēn)布假設），來(lái)計算(suàn)樣本統計量在估計總體統計量時(shí)的(de)誤差。

The central idea is that it may sometimes be better to draw conclusions about the characteristics of a population strictly from the sample at hand, rather than by making perhaps unrealistic assumptions about the population. -- Mooney & Duval, Bootstrapping, 1993

目标夠偉大(dà)（樣本數據自力更生），但具體要怎麽做(zuò)呢(ne)？如何僅僅通(tōng)過（反複的(de)）使用(yòng)手頭的(de)數據來(lái)對(duì)同樣從這(zhè)些數據中得(de)到的(de)統計量進行誤差估計呢(ne)？這(zhè)裏面要用(yòng)到一個(gè)非常重要的(de)技巧：可(kě)置換的(de)重采樣（resampling with replacement）。在這(zhè)個(gè)定義中，“可(kě)置換”是核心。什(shén)麽是“可(kě)置換”呢(ne)？舉個(gè)例子。假設袋子裏有标号 1 到 10 的(de)小球。我們“可(kě)置換”地不斷地從袋子裏随機抽出小球。第一次抽出了(le) 3 号小球；“可(kě)置換”是說在下(xià)一次抽取之前把 3 号小球重新放回到袋子裏；即在第二次抽取的(de)時(shí)候，我們仍然有可(kě)能再次抽到 3 号小球（它和(hé)其他(tā) 9 個(gè)球被抽到的(de)概率是一樣的(de)），這(zhè)便是可(kě)置換的(de)含義。作爲對(duì)比，生活中更多(duō)的(de)是“無置換的(de)抽取”，比如體彩 36 中 7 或者世界杯抽簽，抽出的(de)小球都不會再放回池子中。

下(xià)面就來(lái)看看 Bootstrap 的(de)原則。假設我們有如下(xià)設定：

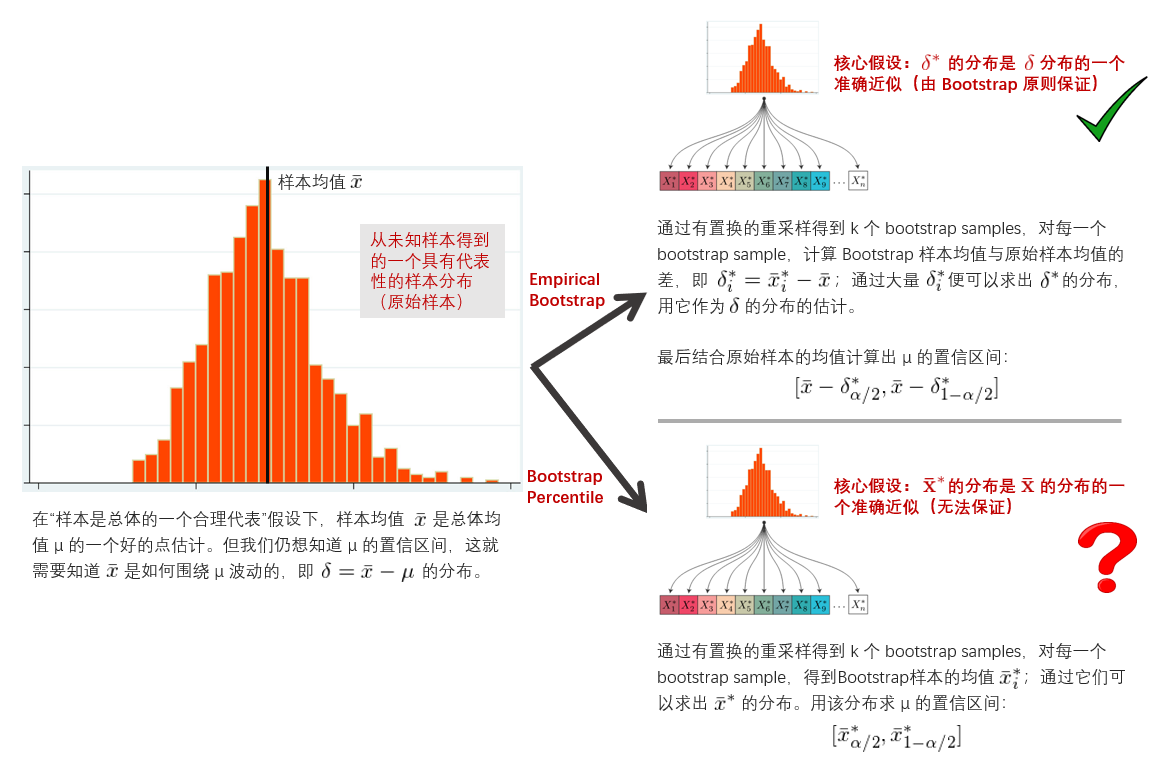
Bootstrap 原則指出：“Bootstrap 樣本統計量 u* 圍繞原始樣本統計量 u 的(de)變化(huà)（簡稱爲 u* 的(de)變化(huà)）” 是 “原始樣本統計量 u 圍繞總體統計量 v 的(de)變化(huà)（簡稱爲 u 的(de)變化(huà)）” 的(de)一個(gè)很好的(de)近似。

爲了(le)計算(suàn) u* 的(de)變化(huà)，我們隻需要對(duì)原始樣本數據進行大(dà)量的(de)可(kě)置換重采樣（爲此需要使用(yòng)計算(suàn)機的(de)計算(suàn)能力，在沒有計算(suàn)機的(de)年代，手動進行大(dà)量重采樣的(de)工作量可(kě)想而知），得(de)到許多(duō) Bootstrap 樣本，并從每個(gè)樣本中計算(suàn)出統計量 u* 的(de)一個(gè)取值，這(zhè)些取值便構成 u* 的(de)分(fēn)布。使用(yòng) u* 的(de)分(fēn)布計算(suàn)出 u* 如何圍繞 u 變化(huà)，以此來(lái)推斷統計量 u 如何圍繞 v 變化(huà)。顯然，統計量 u 的(de)變化(huà)與樣本大(dà)小有關。因此用(yòng) u* 的(de)變化(huà)作爲 u 的(de)變化(huà)的(de)近似的(de)前提是每個(gè) Bootstrap 樣本的(de)大(dà)小和(hé)原始樣本大(dà)小相同。根據 Bootstrap 原則，使用(yòng)經驗 Bootstrap 方法（empirical Bootstrap method）就可(kě)以計算(suàn)任何總體統計量的(de)置信區(qū)間。

3 經驗 Bootstrap 方法

我們以計算(suàn)某未知分(fēn)布均值的(de)置信區(qū)間爲例說明(míng)經驗 Bootstrap 方法。假設我們從某未知分(fēn)布的(de)總體中得(de)到下(xià)面 10 個(gè)樣本數據：30，37，36，43，42，48，43，46，41，42。我們的(de)問題有兩個(gè)：（1）估計總體的(de)均值（點估計），（2）計算(suàn)置信水(shuǐ)平爲 80% 的(de) Bootstrap 置信區(qū)間。第一個(gè)問題很容易回答(dá)，樣本均值 40.8 就是總體均值 μ 的(de)點估計。對(duì)于第二個(gè)問題，由于樣本點太少（僅有 10 個(gè)）且總體分(fēn)布未知（無法做(zuò)正态分(fēn)布假設），因此我們摒棄傳統的(de)方法，而采用(yòng)經驗 Bootstrap 方法計算(suàn)其置信區(qū)間。

計算(suàn) μ 的(de)置信區(qū)間的(de)本質是回答(dá)這(zhè)樣一個(gè)問題：樣本均值 \bar x 的(de)分(fēn)布是如何圍繞總體均值 μ 變化(huà)的(de)。換句話(huà)說，我們想知道 δ = \bar x – μ 的(de)分(fēn)布。δ 就是當我們使用(yòng) \bar x 來(lái)估計 μ 時(shí)的(de)誤差。

如果我們知道 δ 的(de)分(fēn)布，則可(kě)以找到待求置信區(qū)間左右兩端的(de)臨界值。在本例中，因爲我們關心的(de)是置信水(shuǐ)平爲 80% 的(de)置信區(qū)間，因此 δ 的(de)臨界值是 10% 和(hé) 90% 分(fēn)位對(duì)應的(de) δ_{0.9} 和(hé) δ_{0.1}。由此計算(suàn)出 μ 置信區(qū)間爲：

這(zhè)是因爲：

值得(de)一提的(de)是，上面的(de)概率是條件概率，它表示假設總體均值爲 μ 的(de)條件下(xià)，樣本均值 \bar x 圍繞總體均值 μ 的(de)變化(huà)在 δ_{0.1} 和(hé) δ_{0.9} 之間的(de)概率。不幸的(de)是，由于來(lái)自總體的(de)樣本隻有一個(gè)（上面的(de) 10 個(gè)數）且 μ 的(de)真實值未知，我們并不知道 δ 的(de)分(fēn)布（因此也(yě)就不知道 δ_{0.9} 和(hé) δ_{0.1}）。但是我們仍然利器在手，那就是 Bootstrap 原則。它指出雖然我們不知道 \bar x 如何圍繞 μ 變化(huà)（即 δ 的(de)分(fēn)布），但是它可(kě)以由 \bar x* 如何圍繞 \bar x 變化(huà)（即 δ* 的(de)分(fēn)布）來(lái)近似，這(zhè)裏 δ* 是利用(yòng) Bootstrap 樣本計算(suàn)的(de)均值與原始樣本均值之間的(de)差：

通(tōng)過進行多(duō)次有置換的(de)重采樣，得(de)到多(duō)個(gè) Bootstrap 樣本，每一個(gè)樣本中都可(kě)以計算(suàn)出一個(gè)均值。使用(yòng)每一個(gè) Bootstrap 樣本均值減去原始樣本均值（40.8）就得(de)到 δ* 的(de)一個(gè)取值。利用(yòng)計算(suàn)機，很容易産生足夠多(duō)的(de) Bootstrap 樣本，即足夠多(duō)的(de) δ* 的(de)取值。根據大(dà)數定理(lǐ)（law of large numbers），随著(zhe)樣本個(gè)數的(de)增加， δ* 的(de)分(fēn)布也(yě)越來(lái)越精确。有了(le) δ* 的(de)分(fēn)布，就可(kě)以找到 δ*_{0.9} 和(hé) δ*_{0.1}，并用(yòng)它們作爲 δ_{0.9} 和(hé) δ_{0.1} 的(de)估計，從而計算(suàn)出 μ 的(de)置信區(qū)間：

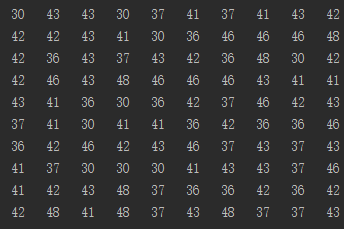
上述思路就是經驗 Bootstrap 方法的(de)強大(dà)所在。回到上面這(zhè)個(gè)例子中。利用(yòng)計算(suàn)機産生 200 個(gè) Bootstrap 樣本（下(xià)圖顯示了(le)前 10 個(gè) Bootstrap 樣本，每列一個(gè)）。

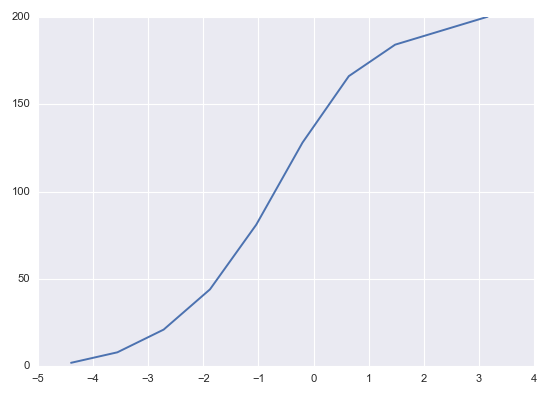
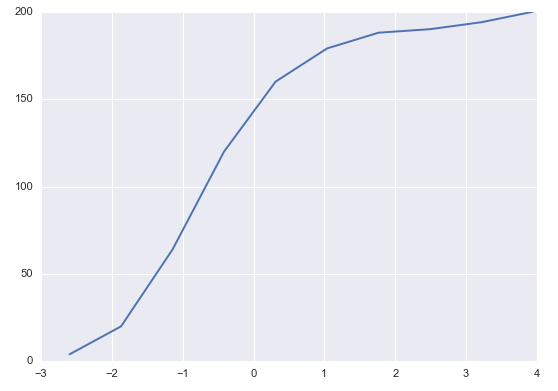
由這(zhè) 200 個(gè) Bootstrap 樣本計算(suàn)出 200 個(gè) δ*，它們的(de)取值範圍在 -4.4 到 4.0 之間，δ* 的(de)累積密度函數如下(xià)圖所示。

接下(xià)來(lái)，從這(zhè) 200 個(gè) δ* 中找出 δ*_{0.9} 和(hé) δ*_{0.1}。由于 δ*_{0.9} 對(duì)應的(de)是 10% 分(fēn)位數，而 δ*_{0.1} 對(duì)應的(de)是 90% 分(fēn)位數，我們将 200 個(gè) δ* 從小到大(dà)排序，其中第 20 個(gè)和(hé)第 181 個(gè)就是我們需要的(de)數值：δ*_{0.9} = -1.9 以及 δ*_{0.1} = 2.2。由于原始樣本均值爲 40.8，因此求出 μ 的(de) 80% 的(de)置信區(qū)間爲：

4 Bootstrap 百分(fēn)位法

讓我們來(lái)看看另外一種方法：Bootstrap 百分(fēn)位法（Bootstrap percentile method）。它與經驗 Bootstrap 方法的(de)不同之處在于，它不是用(yòng) δ* 的(de)分(fēn)布去近似 δ 的(de)分(fēn)布，而是直接使用(yòng)來(lái)自 Bootstrap 樣本的(de)統計量的(de)分(fēn)布作爲原始樣本統計量的(de)分(fēn)布。

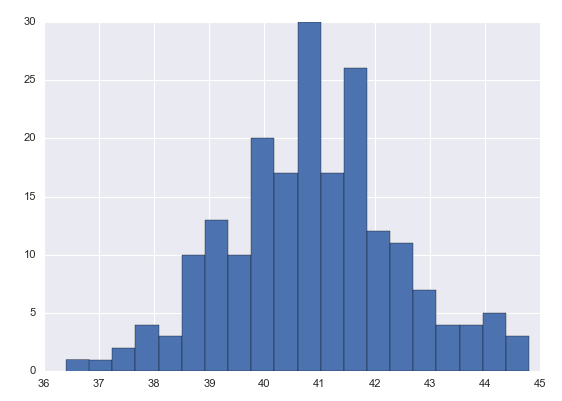
讓我們仍然用(yòng)上一節中的(de)例子來(lái)說明(míng)這(zhè)種方法。在那個(gè)例子中，我們對(duì)原始樣本數據進行有置換的(de)重采樣，得(de)到了(le) 200 個(gè) Bootstrap 樣本。對(duì)于每個(gè)樣本，計算(suàn)出樣本均值，因此一共有 200 個(gè)均值，它們構成了(le) Bootstrap 樣本統計量 \bar x* 的(de)分(fēn)布（下(xià)圖）。

Bootstrap 百分(fēn)位法使用(yòng)來(lái)自 Bootstrap 樣本統計量 \bar x* 的(de)分(fēn)布作爲原始樣本統計量 \bar x 的(de)分(fēn)布的(de)一個(gè)近似。因此，在這(zhè)種方法下(xià)，我們隻需要找到 \bar x* 分(fēn)布中 10% 分(fēn)位和(hé) 90% 分(fēn)位對(duì)應的(de) \bar x* 的(de)取值，它們就構成了(le) μ 的(de)置信區(qū)間。在本例中，這(zhè)兩個(gè)分(fēn)位對(duì)應的(de) \bar x* 的(de)取值分(fēn)别爲 38.9 和(hé) 43，因此按這(zhè)種方法得(de)到的(de) μ 的(de)置信區(qū)間爲：[38.9, 43]。不難發現，上述兩種方法得(de)到的(de)置信區(qū)間并不相同。它們是各有千秋還(hái)是說其中一個(gè)更準确呢(ne)？經驗 Bootstrap 法和(hé) Bootstrap 百分(fēn)位法的(de)區(qū)别如下(xià)：

Bootstrap 原則傳達的(de)是這(zhè)樣一個(gè)意思：樣本統計量 \bar x 是以總體統計量 μ 爲中心圍繞其波動；Bootstrap 樣本統計量 \bar x* 是以原始樣本統計量 \bar x 爲中心圍繞其波動。如果 \bar x 和(hé) μ 有較大(dà)的(de)差異，則 \bar x 和(hé) \bar x* 的(de)分(fēn)布也(yě)會不同（即 Bootstrap 百分(fēn)位法的(de)假設不成立）。反觀 δ 和(hé) δ*，它們的(de)分(fēn)布各自描述 \bar x 如何圍繞 μ 波動以及 \bar x* 如何圍繞 \bar x 波動。Bootstrap 原則指出即使 \bar x 和(hé) \bar x* 分(fēn)布不同，δ* 的(de)分(fēn)布仍然是 δ 的(de)分(fēn)布的(de)一個(gè)很好的(de)近似，因此以原始樣本均值 \bar x 爲中心，以 δ* 的(de)分(fēn)布計算(suàn)出誤差，最終得(de)到的(de) μ 的(de)置信區(qū)間是比較準确的(de)。由此可(kě)知，經驗 Bootstrap 方法優于 Bootstrap 百分(fēn)位法。在實踐中，應該使用(yòng)前者。下(xià)圖概括了(le)上文中對(duì)二者的(de)比較。

5 Bootstrapped-t 方法

除了(le)上面介紹的(de)兩種方法外，最後我還(hái)想再提另一種方法：Bootstrapped-t 方法。這(zhè)種方法和(hé)第一節中介紹的(de)傳統方法十分(fēn)接近。在傳統方法中，基于 Normal Theory 的(de)假設，我們隻需要知道 t 統計量的(de)臨界值就可(kě)以計算(suàn)均值的(de)置信區(qū)間。傳統方法假設待估計的(de)統計量的(de)分(fēn)布是對(duì)稱的(de)。然而在現實問題中，這(zhè)個(gè)假設可(kě)能無法滿足，所以假設對(duì)稱并通(tōng)過查表找出 t 統計量的(de)臨界值會有問題（因爲得(de)到的(de)置信區(qū)間是對(duì)稱的(de)）。由此提出了(le) Bootstrapped-t 方法。

這(zhè)種方法的(de)核心思想是将每個(gè) Bootstrap 樣本中計算(suàn)的(de)統計量轉化(huà)成一個(gè)對(duì)應的(de) t 統計量。這(zhè)樣，有多(duō)少個(gè) Bootstrap 樣本我們就有多(duō)少個(gè) Bootstrapped t 統計量。由此，可(kě)以計算(suàn)出 Bootstrapped t 統計量的(de)分(fēn)布。用(yòng)這(zhè)個(gè)分(fēn)布代替查表來(lái)找到計算(suàn)置信區(qū)間時(shí)所需的(de) t 統計量的(de)臨界值，從而計算(suàn)置信區(qū)間：

其中 s_{\bar x} 是 \bar x 的(de) standard error。以均值爲例，可(kě)以通(tōng)過下(xià)面的(de)關系式将每個(gè) Bootstrap 樣本的(de)均值轉化(huà)爲對(duì)應的(de) Bootstrapped t 統計量（注：如果研究的(de)對(duì)象不是均值，則 Bootstrapped t 統計量會出現不存在解析式的(de)情況）：

其中，\bar x*_i 和(hé) s*_i 分(fēn)别爲第 i 個(gè) Bootstrap 樣本的(de)均值和(hé)标準差；n 爲樣本大(dà)小。仍以前面的(de)例子說明(míng)這(zhè)種方法如何計算(suàn) μ 的(de)置信區(qū)間。對(duì)于每個(gè) Bootstrap 樣本，計算(suàn)其 Bootstrapped t 統計量，它們的(de)累積密度函數爲：

通(tōng)過 Bootstrapped t 統計量很容易找到臨界值 -1.17 和(hé) 1.81。因此，μ 的(de)置信區(qū)間爲：[31.82, 46.62]。這(zhè)個(gè)置信區(qū)間的(de)範圍遠(yuǎn)遠(yuǎn)大(dà)于前面兩種方法的(de)置信區(qū)間。介紹這(zhè)種方法的(de)目的(de)是爲了(le)給讀者開拓思路。在實踐中推薦使用(yòng)經驗 Bootstrap 方法。

6 不止均值

到目前未知，本文的(de)例子中均已均值作爲目标統計量，這(zhè)便于将不同的(de) Bootstrap 方法得(de)到的(de)置信區(qū)間進行比較。然而，Bootstrap 方法在計算(suàn)置信區(qū)間時(shí)可(kě)以考慮各種傳統方法無能爲力的(de)統計量。下(xià)面就來(lái)看看中位數的(de)例子。仍然以第三節中的(de)十個(gè)數（30，37，36，43，42，48，43，46，41，42）作爲來(lái)自某個(gè)未知總體的(de)一組樣本。采用(yòng)經驗 Bootstrap 方法，我們來(lái)計算(suàn)中位數的(de) 95% 的(de)置信區(qū)間。使用(yòng)之前用(yòng)到的(de) 200 個(gè) Bootstrap 樣本，可(kě)以得(de)到中位數誤差的(de)臨界值。由于考慮的(de)是 95% 的(de)置信區(qū)間，因此臨界值爲 2.5% 和(hé) 97.5% 分(fēn)位對(duì)應的(de)誤差：-5.0 和(hé) 2.5。從原始數據易知，樣本的(de)中位數是 42。因此，中位數的(de) 95% 的(de)置信區(qū)間爲：[39.5, 47]。

7 Bootstrap 與量化(huà)投資

本文介紹了(le)如何使用(yòng) Bootstrap 技術計算(suàn)參數估計的(de)誤差。Bootstrap 方法對(duì)總體分(fēn)布不做(zuò)假設，且可(kě)以被應用(yòng)于我們感興趣的(de)各種統計量，這(zhè)些特點使得(de)它非常強大(dà)。當然，需要說明(míng)的(de)是 Bootstrap 中的(de)重采樣并不能夠幫助我們改進點估計（point estimate）。以均值爲例，原始樣本均值 \bar x 就是總體均值 μ 的(de)點估計。我們使用(yòng)重采樣得(de)到很多(duō) Bootstrap 樣本，并且得(de)到很多(duō) Bootstrap 樣本均值 \bar x*，則這(zhè)些 \bar x* 的(de)平均值将會非常接近 \bar x （事實上，可(kě)以證明(míng) E[\bar x*] —— \bar x* 的(de)期望 —— 就是 \bar x）。換句話(huà)說，對(duì)于點估計，Bootstrap 樣本均值并不能比 \bar x 提供任何新的(de)信息。但是，這(zhè)些 \bar x* 的(de)取值對(duì)于估計 \bar x 如何圍繞 μ 變化(huà)非常有效，這(zhè)便是我們在全文中反複強調的(de) Bootstrap 的(de)核心。

在量化(huà)投資領域，Bootstrap 也(yě)有廣泛的(de)應用(yòng)。例如，Bootstrap 可(kě)以用(yòng)來(lái)對(duì)參數估計的(de)偏差進行修正，比如投資品收益率之間的(de)相關系數。投資品的(de)曆史收益率數據就是我們僅有的(de)樣本，通(tōng)過重采樣并利用(yòng)經驗 Bootstrap 方法，可(kě)以求出各種統計量的(de)估計誤差，這(zhè)無疑有助于我們更好的(de)構建投資策略，進行風險防控。又比如，簡單的(de)分(fēn)類算(suàn)法（比如分(fēn)類樹）可(kě)以用(yòng)來(lái)進行選股，但是它對(duì)樣本數據比較敏感，預測的(de)方差較大(dà)。在這(zhè)方面可(kě)以采用(yòng) Bootstrap 技巧作爲元算(suàn)法技術用(yòng)于一般分(fēn)類算(suàn)法（比如結合 Bootstrap 和(hé)分(fēn)類樹得(de)到的(de)裝袋算(suàn)法），這(zhè)可(kě)以明(míng)顯地降低分(fēn)類算(suàn)法的(de)方差，從而提高(gāo)預測的(de)準确性（感興趣的(de)讀者請看《“少樹”服從“多(duō)樹”（下(xià)）》）。

最後，本文介紹的(de)幾種方法都屬于無參數 Bootstrap 方法，即對(duì)總體分(fēn)布不做(zuò)任何假設。在一些應用(yòng)中，如果能夠明(míng)确總體分(fēn)布的(de)類型，也(yě)可(kě)以使用(yòng) Bootstrap 方法進行參數估計，這(zhè)稱之爲參數化(huà) Bootstrap 方法。比如，我們已知總體分(fēn)布滿足指數分(fēn)布，但是不知道其參數 λ。這(zhè)時(shí)，可(kě)以利用(yòng)參數化(huà) Bootstrap 方法計算(suàn)出 Bootstrap 樣本中 λ* 的(de)誤差的(de)分(fēn)布，用(yòng)它來(lái)估計 λ 的(de)置信區(qū)間。由于空間有限，本文不再展開介紹。

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。