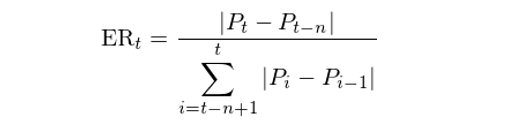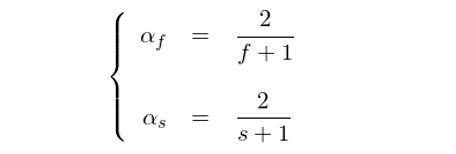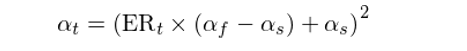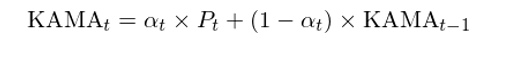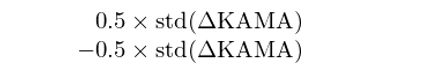精選技術指标系列（4）：KAMA

作者：石川

摘要：考夫曼自适應均線是一個(gè)優秀的(de)移動平均算(suàn)法，它根據價格噪聲大(dà)小動态決定均線的(de)衰減系數，在快(kuài)、慢(màn)均線之間切換。

1 引言

本期精選技術指标聊一聊考夫曼自适應移動平均（Kaufman Adaptive Moving Average，簡稱 KAMA）。它由系統分(fēn)析大(dà)師佩裏 • 考夫曼（Perry Kaufman）發明(míng)，是一種高(gāo)級均線算(suàn)法，能根據價格曲線噪聲的(de)大(dà)小自動确定計算(suàn)價格均線時(shí)的(de)衰減系數。我們重點講一講 KAMA 作爲移動平均線的(de)特點和(hé)優勢，并将它利用(yòng)到不同投資品的(de)價格上，說明(míng)它作爲一個(gè)系統交易工具的(de)作用(yòng)。

2 從價格噪聲說起 —— 效率比

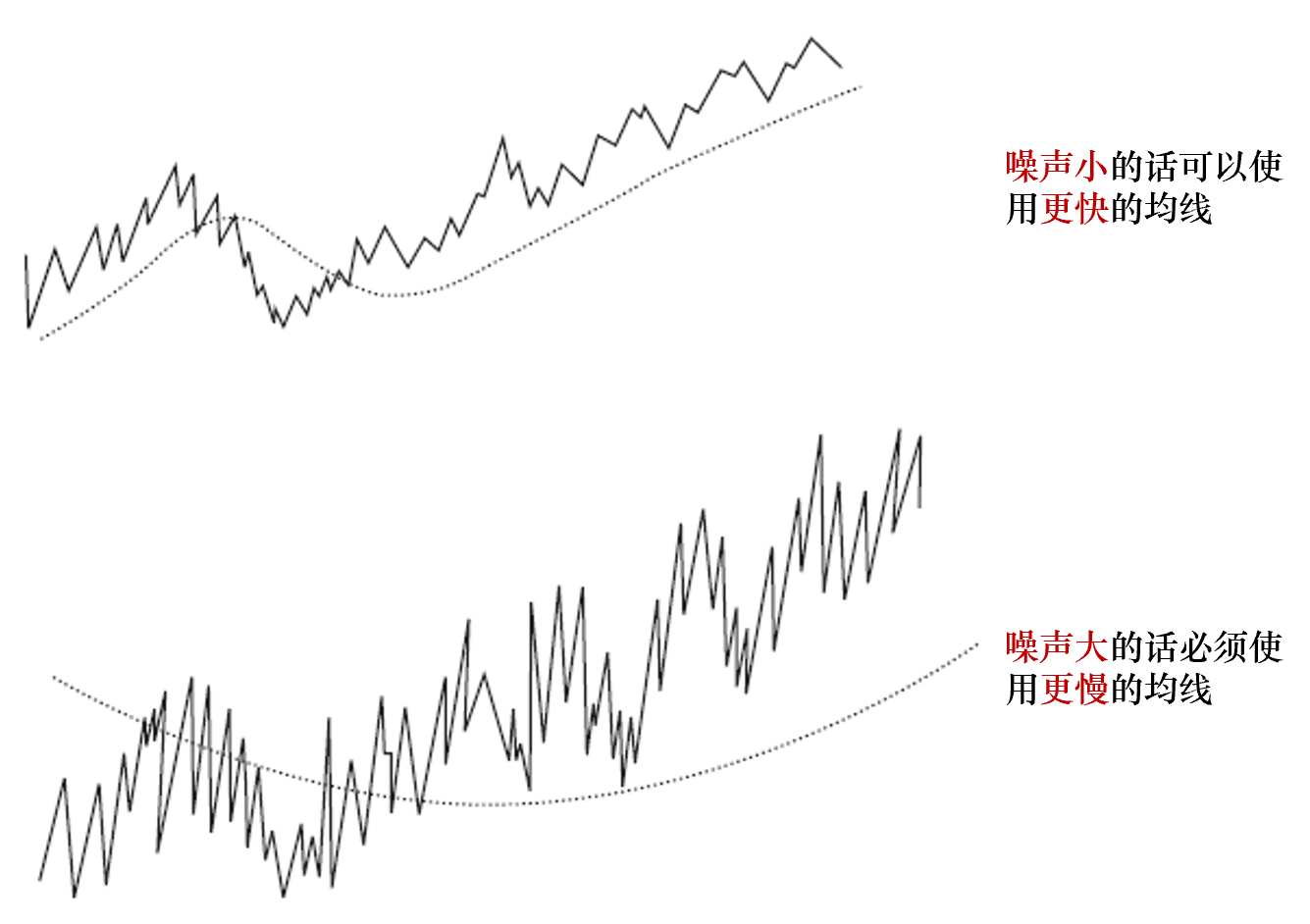
移動平均的(de)目的(de)是捕捉價格曲線的(de)低頻(pín)趨勢，而趨勢很容易被掩蓋在噪聲之中，因此價格噪聲無疑是移動平均的(de)敵人(rén)。如果價格的(de)噪聲很小，我們則可(kě)以利用(yòng)塊均線捕捉趨勢（比如 10 日或者 20 日均線）；而如果價格的(de)噪聲太大(dà)，就要使用(yòng)更慢(màn)的(de)均線（比如 50 日或者 100 日均線）。

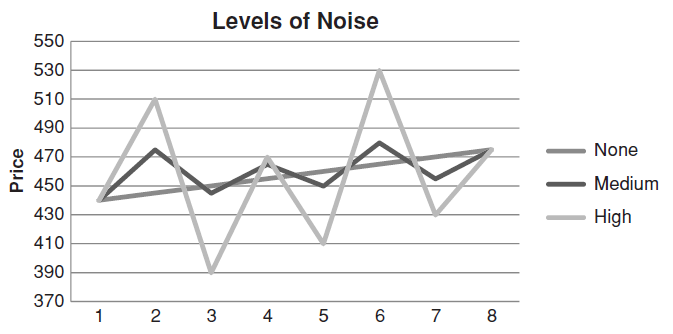
可(kě)見，價格均線如果想要有“自适應性”，就必須考慮價格曲線的(de)噪聲。這(zhè)就是考夫曼移動平均的(de)出發點。在 KAMA 中，如何衡量噪聲的(de)大(dà)小呢(ne)？來(lái)看下(xià)面這(zhè)個(gè)例子。下(xià)圖爲三條假想的(de)價格曲線：它們在初期和(hé)末期的(de)價格都相同——即在這(zhè)段時(shí)間中，價格的(de)淨變化(huà)（net move）都是一樣的(de)——但是這(zhè)三條曲線實現這(zhè)個(gè)淨變化(huà)的(de)軌迹卻大(dà)相徑庭。這(zhè)三條價格曲線中：

這(zhè)個(gè)例子給我們一個(gè)啓發：對(duì)于給定的(de)計算(suàn)窗(chuāng)口，在同樣的(de)淨變化(huà)下(xià)（即價格的(de)位移），價格曲線軌迹的(de)路程越大(dà)則價格的(de)噪聲越高(gāo)。将上面這(zhè)句話(huà)翻譯成數學，就得(de)到了(le)一個(gè)定量衡量價格噪聲的(de)指标 —— 效率比（efficiency ratio）。它的(de)定義如下(xià)：

其中，P_t 是時(shí)刻 t 的(de)價格，n 爲時(shí)間窗(chuāng)口，ER_t 則爲 t 時(shí)刻的(de)效率比。效率比的(de)取值在 0 和(hé) 1 之間，它越大(dà)說明(míng)噪聲越低。上面這(zhè)三條假想的(de)價格曲線的(de)效率比分(fēn)别爲 1.0（無噪聲）、0.56（低噪聲）、和(hé) 0.06（高(gāo)噪聲）。

有了(le)計算(suàn)噪聲的(de)方法後，考夫曼所做(zuò)的(de)就是用(yòng)它來(lái)計算(suàn)指數平滑中的(de)衰減系數 α，從而實現“在噪聲高(gāo)時(shí)，使用(yòng)慢(màn)均線，即更低的(de) α；在噪聲低時(shí)，使用(yòng)快(kuài)均線，即更高(gāo)的(de) α”。這(zhè)就是考夫曼均線的(de)核心 —— 使用(yòng)指數平滑計算(suàn)移動均線，計算(suàn)時(shí)根據價格的(de)效率比動态的(de)調整指數平滑的(de)參數 α，α 與效率比正相關。下(xià)面就來(lái)看看考夫曼均線的(de)具體計算(suàn)公式。

3 考夫曼自适應移動平均

在考夫曼均線 KAMA 的(de)計算(suàn)中，用(yòng)到了(le)快(kuài)、慢(màn)兩個(gè)時(shí)間窗(chuāng)口，它們作爲輸入的(de)常數，用(yòng)于産生快(kuài)、慢(màn)兩個(gè)默認的(de)衰減系數。令 f（fastest）和(hé) s（slowest）分(fēn)别代表快(kuài)、慢(màn)兩個(gè)時(shí)間窗(chuāng)口的(de)長(cháng)度，則這(zhè)兩個(gè)默認的(de)衰減系數爲：

這(zhè)兩個(gè)默認的(de)衰減系數相當于 KAMA 所采用(yòng)的(de)衰減系數兩個(gè)極限情況（一旦 f 和(hé) s 的(de)數值給定，這(zhè)兩個(gè)默認衰減系數也(yě)不再變化(huà)；對(duì)于 KAMA 來(lái)說它們是常數）。前面說過，KAMA 的(de)本質是動态計算(suàn)衰減系數的(de)指數平均。它的(de)衰減系數是上述這(zhè)兩個(gè)默認值 α_f 和(hé) α_s，以及效率比的(de)函數。在 t 時(shí)刻，KAMA 的(de)衰減系數爲：

由上一節的(de)介紹可(kě)知，ER_t 是時(shí)間窗(chuāng)口 n 内的(de)效率比（因此，計算(suàn) ER 的(de)時(shí)間窗(chuāng)口 n 便是計算(suàn) KAMA 的(de)第三個(gè)，也(yě)是最後一個(gè)參數）。如果在這(zhè)段時(shí)間内價格單方向運動（即連漲或者連跌），那麽 ER_t 的(de)取值爲 1；如果在這(zhè)段時(shí)間内價格反複波動而位移卻爲 0，則 ER_t 的(de)取值爲 0。當這(zhè)兩種極端情況出現時(shí)：

在 KAMA 的(de)計算(suàn)公式中，f 和(hé) s 的(de)默認取值爲 2 和(hé) 30。由于上述計算(suàn) α_t 的(de)公式中有一個(gè)二次方，因此實際上在上述兩種極端情況下(xià)，α_t 對(duì)應的(de)是時(shí)間窗(chuāng)口長(cháng)度爲 4 和(hé) 900 的(de)快(kuài)、慢(màn)均線，因此 KAMA 有時(shí)可(kě)以很快(kuài)、有時(shí)又會很慢(màn)，這(zhè)完全取決于噪聲的(de)大(dà)小。在實際使用(yòng)時(shí)，使用(yòng)者應根據投資品價格的(de)實際特征确定 f 和(hé) s 的(de)最佳取值。當然，上述極端情況很不容易出現。在一般情況下(xià)，ER_t 是一個(gè) 0 到 1 之間的(de)數，因此效率比又被稱爲分(fēn)形效率（fractal efficiency）。從公式中容易看出，

得(de)到當期的(de)衰減系數 α_t 之後，就可(kě)以将指數平均算(suàn)法作用(yòng)于價格序列 P_t 之上，求出價格序列的(de)考夫曼均線 KAMA：

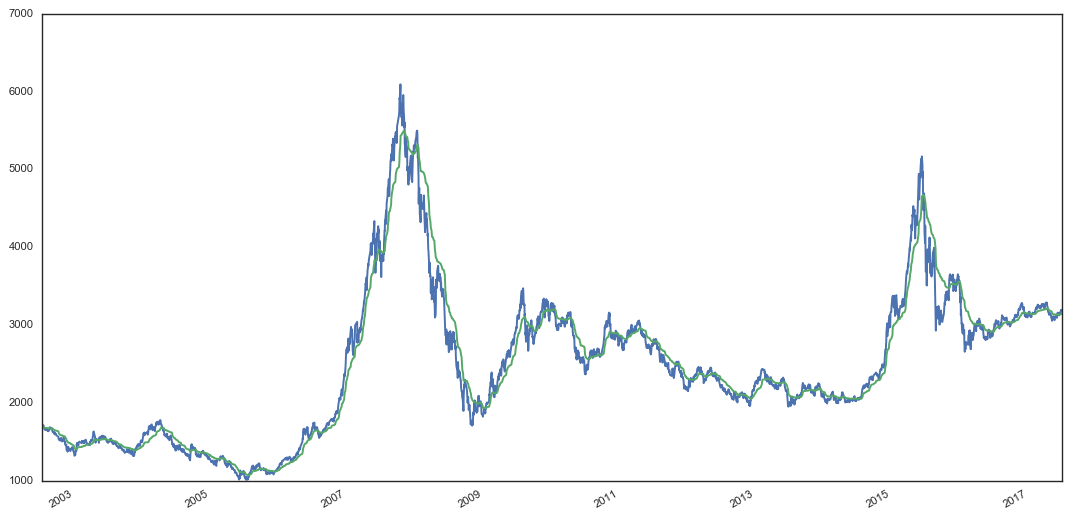
由上面的(de)介紹可(kě)知，計算(suàn) KAMA 需要三個(gè)參數，它們是計算(suàn)效率比的(de)窗(chuāng)口 n、以及計算(suàn)快(kuài)、慢(màn)兩個(gè)默認衰減系數的(de)窗(chuāng)口 f 和(hé) s。以上證指數的(de)日收盤價爲例爲例，下(xià)圖爲 n = 8，f = 5，s = 30 時(shí)的(de)考夫曼自适應均線（綠色）和(hé)上證指數收盤價的(de)比較。

無論是在趨勢明(míng)顯的(de)牛熊市還(hái)是在糾結的(de)震蕩市中，KAMA 都比較平滑，并沒有出現在震蕩市中反複變化(huà)均線方向的(de)情況。這(zhè)得(de)益于它在震蕩市中可(kě)以自适應的(de)根據市場(chǎng)的(de)噪聲決定采用(yòng)更長(cháng)周期的(de)均線來(lái)過濾掉過高(gāo)的(de)噪聲。而在牛熊市交替的(de)時(shí)候，KAMA 的(de)反應速度也(yě)比較令人(rén)滿意，它十分(fēn)果斷的(de)改變方向。這(zhè)相對(duì)于長(cháng)周期的(de)簡單移動平均來(lái)說無疑大(dà)大(dà)降低了(le)滞後性。下(xià)面就來(lái)看看使用(yòng) KAMA 擇時(shí)的(de)效果。

4 基于 KAMA 的(de)簡單擇時(shí)

由于 KAMA 捕捉低頻(pín)趨勢，因此我們可(kě)以基于此構建一個(gè)簡單的(de)純多(duō)頭股票(piào)擇時(shí)策略：

這(zhè)裏正、負阈值分(fēn)别爲：

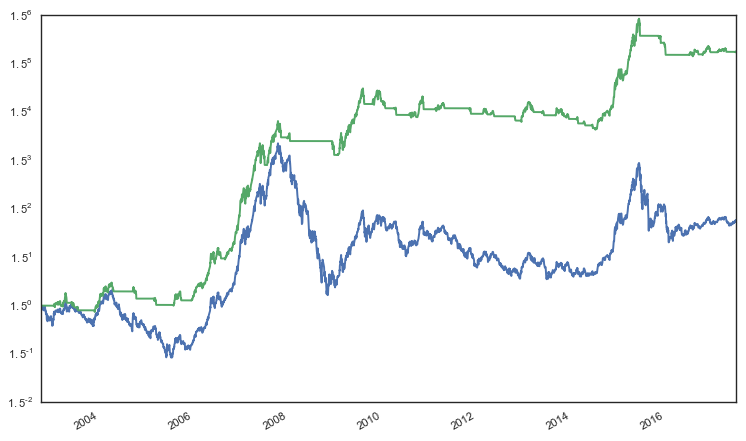
其中 ΔKAMA 爲 KAMA 的(de)變化(huà)量，std 爲求它的(de)标準差。假設每次的(de)交易成本爲萬分(fēn)之五。在計算(suàn) KAMA 時(shí)，參數爲 n = 8，f = 5，s = 30；并且采用(yòng)滾動窗(chuāng)口爲 50 計算(suàn)上述正、負阈值。該策略在上證指數上的(de)擇時(shí)效果如下(xià)圖所示。

圖中，綠色 KAMA 擇時(shí)淨值，而藍色爲基準指數本身的(de)淨值。在過去 15 年裏，KAMA 簡單擇時(shí)策略可(kě)以取得(de) 15.5% 的(de)連續複利年化(huà)收益，夏普率 0.853，最大(dà)回撤爲 -29.3%。這(zhè)些指标遠(yuǎn)超基準指數本身。

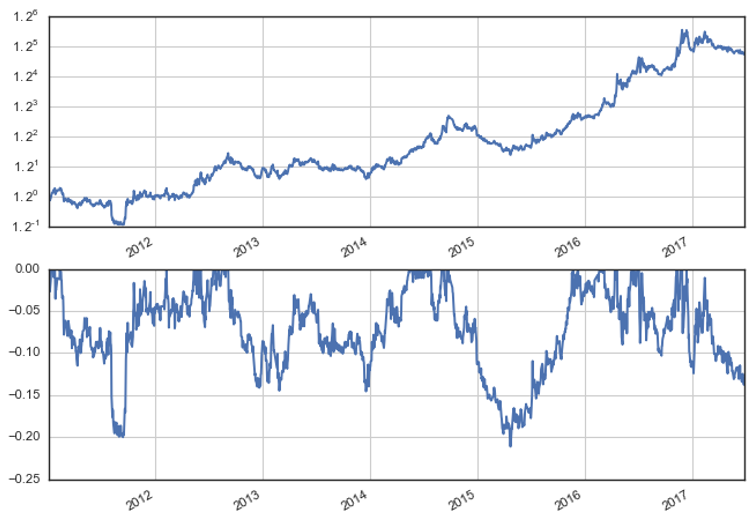
最後再來(lái)看看 KAMA 在商品期貨上面的(de)效果。交易品種爲如下(xià)商品期貨的(de)合成指數：鄭商所的(de)棉花、大(dà)商所的(de)豆粕以及上期所的(de)螺紋鋼、橡膠和(hé)滬鋅。每筆最大(dà)虧損定爲資金量的(de) 2%，并采用(yòng)跟蹤止損。假設在每日收盤後利用(yòng)最新價格數據計算(suàn) KAMA，并通(tōng)過判斷它的(de)變化(huà)是否超過正、負阈值決定是否産生交易信号（由于商品期貨可(kě)以做(zuò)空，因此當 KAMA 均線向下(xià)且超過負阈值時(shí)，我們用(yòng)做(zuò)空取代股票(piào)策略中的(de)空倉）。如果産生了(le)交易信号，則按下(xià)一個(gè)交易日的(de)開盤價執行。每筆交易的(de)手續費和(hé)滑點之和(hé)爲千分(fēn)之一。

在從 2011 年開始的(de)回測期内，KAMA 簡單擇時(shí)策略可(kě)以獲得(de) 14.4% 的(de)連續複利年化(huà)收益，最大(dà)回撤 -21.13%，夏普率 0.871。本文的(de)目的(de)是爲了(le)說明(míng) KAMA 的(de)原理(lǐ)和(hé)特點，因此我們對(duì) KAMA 的(de)擇時(shí)策略的(de)討(tǎo)論到此爲止。

5 結語

移動平均線是技術分(fēn)析中一種分(fēn)析投資品價格時(shí)間序列的(de)常用(yòng)工具。移動平均可(kě)過濾掉價格的(de)高(gāo)頻(pín)噪聲，反映其中長(cháng)期趨勢，輔助投資者做(zuò)出投資判斷。KAMA 是一個(gè)優秀的(de)移動平均算(suàn)法，它根據價格曲線自身的(de)噪聲大(dà)小動态的(de)決定計算(suàn)均線的(de)衰減系數，從而自動地在快(kuài)、慢(màn)均線之間切換。

無論是什(shén)麽技術指标，若想通(tōng)過它持續地賺到錢，必須充分(fēn)理(lǐ)解該指标的(de)原理(lǐ)和(hé)它反映的(de)本質、并堅持使用(yòng)它。對(duì)于任何指标，必須判斷它是否适合我們面對(duì)的(de)市場(chǎng)。通(tōng)過嚴格的(de)曆史回測和(hé)分(fēn)析，可(kě)以計算(suàn)出技術指标的(de)有效性。此外，随著(zhe)市場(chǎng)自身内在的(de)變化(huà)，回測中有效的(de)技術指标也(yě)許會在将來(lái)的(de)某一天失效。因此我們應用(yòng)動态和(hé)發展的(de)眼光(guāng)看問題，以檢驗指标是否持續有效。

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。