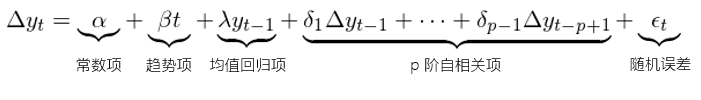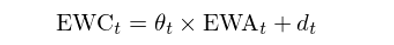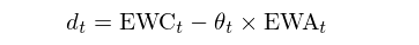均值回歸：循規蹈矩，偶發癫狂

作者：石川

摘要：均值回歸策略在量化(huà)投資中應用(yòng)廣泛。但是它往往“收益有限、風險無限”。本文就來(lái)揭開它神秘的(de)面紗。

1 引言

均值回歸指的(de)是一個(gè)變量随著(zhe)時(shí)間的(de)變化(huà)在其均值上下(xià)波動的(de)現象。

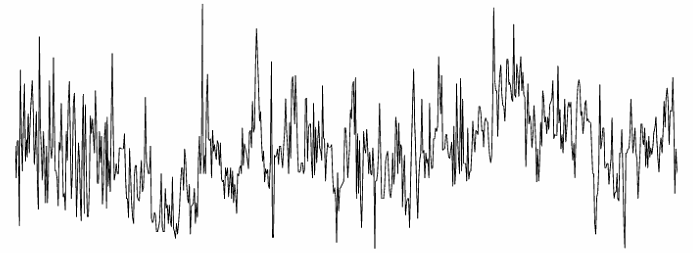
自然科學和(hé)社會科學中都有大(dà)量均值回歸（mean reversion 或 reverting to the mean）的(de)例子。下(xià)圖爲尼羅河(hé)年最低水(shuǐ)位随時(shí)間的(de)變化(huà)，它表現出了(le)明(míng)顯的(de)均值回歸特性。

在社會科學中，諾貝爾獎獲得(de)者、著名的(de)行爲金融學家、展望理(lǐ)論的(de)提出者 Daniel Kahneman 曾提出了(le)一個(gè)“體育畫(huà)報詛咒”的(de)例子：凡是登上體育畫(huà)報封面的(de)明(míng)星，在接下(xià)來(lái)的(de)新賽季的(de)表現都會“跌落人(rén)間”。科學研究表明(míng)，運動員(yuán)的(de)表現也(yě)是圍繞均值呈随機分(fēn)布。因此，上一個(gè)賽季擁有高(gāo)光(guāng)表現的(de)明(míng)星（以至于登上了(le)體育畫(huà)報），有很大(dà)可(kě)能在接下(xià)來(lái)的(de)新賽季變得(de)平庸。換句話(huà)說，運動員(yuán)的(de)表現呈現均值回歸特性。

雖然遠(yuǎn)不如自然和(hé)社會科學中的(de)現象完美(měi)，但是在金融市場(chǎng)投資中也(yě)有近似均值回歸的(de)現象，更是存在大(dà)量的(de)圍繞該現象構建的(de)投資策略。那麽，依靠均值回歸是否能夠掙到錢呢(ne)？這(zhè)樣的(de)策略風險又有多(duō)大(dà)呢(ne)？這(zhè)些就是本文要探討(tǎo)的(de)問題。

2 金融領域的(de)均值回歸

根據維基百科，金融市場(chǎng)的(de)均值回歸定義如下(xià)：

In finance, mean reversion is the assumption that a stock's price will tend to move to the average price over time.

我們可(kě)以把上述定義中的(de)“股票(piào)”換成其他(tā)任何投資品。我想強調的(de)是，這(zhè)個(gè)定義中最核心的(de)兩個(gè)字是價格（而不是投資品的(de)收益率）。這(zhè)一點怎麽強調都不過分(fēn)：

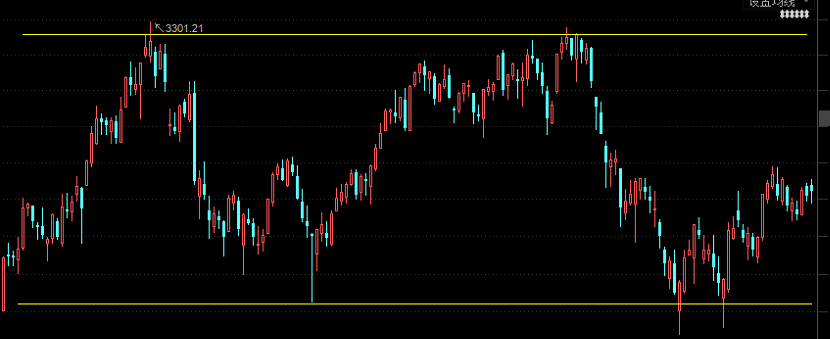
在現實中，絕大(dà)多(duō)數單一（特地提出單一，爲後面留個(gè)伏筆）投資品價格都不滿足均值回歸。如果有明(míng)顯的(de)均值回歸，那麽賺錢就太容易了(le)，我們隻需要做(zuò)到所有那些僞專家說的(de)“高(gāo)抛低吸”。滿足均值回歸時(shí)，由于格在區(qū)間内震蕩且圍繞其均值波動，高(gāo)抛低吸當然是可(kě)能的(de)。比如下(xià)圖是上證指數從 2016 年 11 月(yuè)到現在的(de)波動區(qū)間，上限 3300 附近、下(xià)限 3050 左右。如果它就在這(zhè)個(gè)區(qū)間内呈現均值回歸的(de)話(huà)，那麽我們還(hái)愁賺不著(zhe)錢嗎？

然而，現在來(lái)看都是事後諸葛亮。當我們身在其中的(de)時(shí)候，又有誰敢說上證指數會在這(zhè)個(gè)區(qū)間内震蕩呢(ne)？滿足均值回歸的(de)投資品在現實中幾乎沒有的(de)。如果一個(gè)時(shí)間序列滿足均值回歸，那麽它一定也(yě)滿足平穩性。平穩性要求時(shí)間序列的(de)均值和(hé)方差不随時(shí)間變化(huà)。顯然，投資品的(de)價格無法滿足這(zhè)樣的(de)假設。

現實中，投資品價格基本上都呈現幾何随機遊走（關于這(zhè)方面，感興趣的(de)讀者可(kě)以參考《布朗運動、伊藤引理(lǐ)、BS 公式》和(hé)《寫給你的(de)金融時(shí)間序列分(fēn)析》系列文章(zhāng)）。雖然單一投資品的(de)價格不滿足均值回歸，但幸運的(de)是，我們可(kě)以把多(duō)個(gè)投資品（通(tōng)常是兩個(gè)）線性組合在一起，使它們的(de)價差滿足均值回歸。

在數學上，如果多(duō)個(gè)非平穩的(de)時(shí)間序列通(tōng)過線性組合得(de)到一個(gè)平穩的(de)時(shí)間序列，則把滿足這(zhè)種關系稱爲協整（cointegration）。正因如此，均值回歸這(zhè)種現象才在金融領域才有了(le)廣泛的(de)應用(yòng)。如果一個(gè)價格（或者價差）序列滿足均值回歸，那麽當前的(de)價格對(duì)下(xià)一時(shí)刻價格的(de)變化(huà)應該有預測性。例如，如果當前的(de)價格高(gāo)于均值，那麽下(xià)一時(shí)刻的(de)價格會傾向于朝著(zhe)均值移動。基于這(zhè)樣的(de)假設可(kě)以構建一個(gè)描述均值回歸的(de)線性數學模型。

對(duì)于價格（或多(duō)個(gè)投資品線性組合的(de)價差）序列 y，該模型爲：

我們可(kě)以通(tōng)過曆史數據來(lái)估計模型中的(de)參數。如果 y 滿足均值回歸，那麽這(zhè)個(gè)模型中的(de)參數 λ 就必須在統計上顯著的(de)不爲零（更确切的(de)說，λ 需要顯著爲負）。通(tōng)常可(kě)以使用(yòng) ADF 檢驗（Augmented Dickey-Fuller Test）來(lái)考察 λ 的(de)取值。

一旦找到一個(gè)滿足均值回歸的(de)價格或者價差序列，就可(kě)以用(yòng)它構建一個(gè)均值回歸策略，并利用(yòng)這(zhè)種特性來(lái)賺錢。下(xià)面我們就來(lái)看看一個(gè)經典的(de)例子。

3 配對(duì)交易

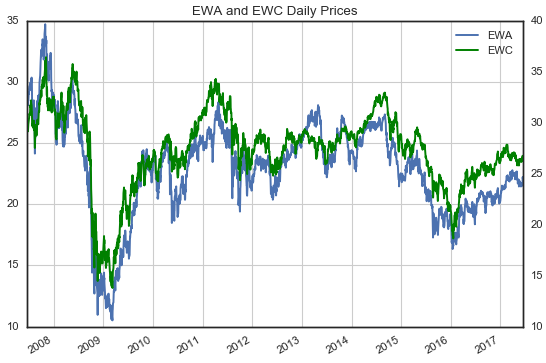
EWA 和(hé) EWC 的(de)配對(duì)交易是均值回歸策略的(de)一個(gè)經典例子。他(tā)們分(fēn)别代表澳大(dà)利亞（EWA）和(hé)加拿大(dà)（EWC）股指的(de)兩個(gè) ETFs。由于這(zhè)兩個(gè)國家的(de)經濟都主要依靠商品，因此我們預期在特定的(de)線性組合下(xià)，這(zhè)兩個(gè) ETFs 的(de)價差滿足均值回歸。爲了(le)驗證這(zhè)一點，首先畫(huà)出這(zhè)兩個(gè) ETFs 的(de)價格序列（下(xià)圖）。可(kě)見，它們确實有很高(gāo)的(de)相似度，當然這(zhè)兩個(gè)價格之間的(de)比例并不是 1:1——在絕大(dà)多(duō)數情況下(xià)，EWA 要比 EWC 高(gāo)一些，它們之間存在一個(gè)随時(shí)間變化(huà)的(de)比例，這(zhè)個(gè)比例也(yě)稱作 hedge ratio。

如果用(yòng) θ_t 來(lái)表示 t 時(shí)刻它們的(de)比例，則可(kě)以構建如下(xià)關系：

換句話(huà)說，d_t 就是它們線性組合得(de)到的(de)價差序列：

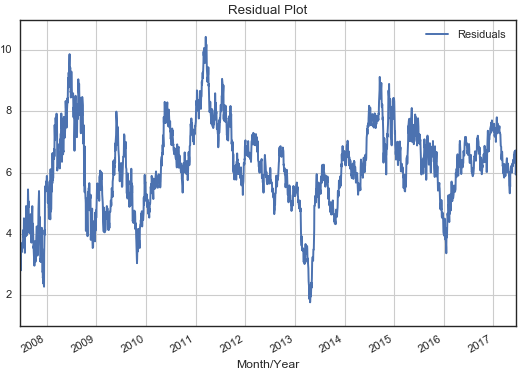
如果我們假設 θ_t 不随時(shí)間變化(huà)而是一個(gè)常數，則可(kě)以用(yòng)這(zhè)兩個(gè)曆史價格序列做(zuò)線性回歸，從而确定 θ 的(de)取值。之後便可(kě)以計算(suàn)它倆線性組合的(de)價差序列，如下(xià)圖所示。

直觀上看，價差序列确實符合均值回歸。對(duì)它進行 ADF 檢驗，得(de)到的(de)統計值爲 -4.09（p-value 爲 0.0065），小于顯著性 1% 對(duì)應的(de)阈值 -3.96，這(zhè)說明(míng)我們可(kě)以在 99% 的(de)置信水(shuǐ)平下(xià)拒絕原假設。ADF 檢驗說明(míng)該價差序列滿足均值回歸。

如何利用(yòng)這(zhè)個(gè)價差序列來(lái)構建量化(huà)策略呢(ne)？首先必須明(míng)确的(de)是，在這(zhè)個(gè)策略中，我們交易的(de)将是這(zhè)個(gè)價差。當價差在均值之下(xià)的(de)時(shí)候，則做(zuò)多(duō)價差；當價差在均值之上的(de)時(shí)候，則做(zuò)空價差。但不要忘記，價差是我們人(rén)爲構建的(de)。因此在實際交易中也(yě)必須通(tōng)過配對(duì)交易 EWC 和(hé) EWA 來(lái)實現對(duì)價差的(de)多(duō)空交易。根據價差的(de)數學表達式，最終的(de)量化(huà)策略爲：

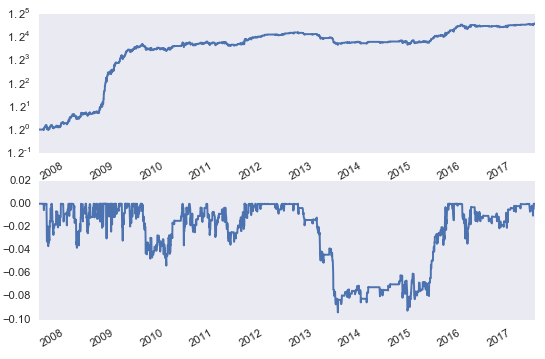
在實際交易中，必須确定多(duō)空雙向交易開倉和(hé)平倉的(de)阈值。此外，我們也(yě)假設這(zhè)兩個(gè)投資品的(de)比例 θ_t 是随時(shí)間變化(huà)的(de)。在我們的(de)實驗中，采用(yòng)狀态空間模型（state space model）中的(de)卡爾曼濾波（Kalman filter）算(suàn)法來(lái)動态确定 θ_t 以及上面提到的(de)阈值的(de)取值。狀态空間模型的(de)思想可(kě)以簡述爲它将 θ_t 看作一個(gè)未知的(de)狀态，并通(tōng)過觀測值來(lái)确定狀态的(de)取值。詳細的(de)介紹超出本文的(de)範疇，我們會在今後某期量化(huà)核武研究專題中介紹狀态空間模型。由于交易的(de)是 ETFs，我們假設萬分(fēn)之三的(de)成本。在這(zhè)種假設下(xià)，上述價差交易策略的(de)淨值曲線和(hé)最大(dà)回撤曲線如下(xià)：

在回測期内，策略的(de)年化(huà)連續複利收益率爲 8.72%，最大(dà)回撤 -9.38%，夏普率 1.00。從淨值和(hé)最大(dà)回撤曲線中看出很大(dà)的(de)一部分(fēn)收益來(lái)自 2009 年；另外，在 2013 年到 2015 年間，策略發生了(le)長(cháng)達 700 多(duō)個(gè)自然日的(de)回撤。盡管如此，策略的(de)整體表現依然算(suàn)是可(kě)圈可(kě)點，因此這(zhè)哥(gē)倆的(de)配對(duì)交易算(suàn)是均值回歸策略裏面的(de)經典案例。

在上面這(zhè)個(gè)例子中，讓我們願意相信該價差能夠維持均值回歸的(de)根本原因是基本面層面的(de)，即澳大(dà)利亞和(hé)加拿大(dà)這(zhè)兩個(gè)國家的(de)經濟都由商品貿易主宰。隻要這(zhè)個(gè)先決條件不變，我們有理(lǐ)由相信它們的(de)價差會一直均值回歸下(xià)去。但是必須說明(míng)的(de)是，與趨勢追蹤策略的(de)“收益無限、風險有限”恰恰相反的(de)是，均值回歸策略“收益有限、風險無限”。當基本面原因的(de)突然消失以及使用(yòng)超高(gāo)杠杆時(shí)，一個(gè)均值回歸策略必然驟然失效、導緻慘痛的(de)虧損。長(cháng)期資本的(de)故事正是如此。

4 長(cháng)期資本的(de)教訓

長(cháng)期資本管理(lǐ)公司（Long-Term Capital Management）曾經是美(měi)國華爾街(jiē)首屈一指的(de)對(duì)沖基金公司，在基本沒有虧損和(hé)回撤的(de)情況下(xià)，取得(de)了(le) 1994 成立至 1997 年輝煌頂峰每年費後 28.5%、42.8%、40.8% 和(hé) 17% 的(de)投資淨回報。1998 年初其淨資産達到 46 億美(měi)元，通(tōng)過 33 倍杠杆控制 1500 億美(měi)元規模的(de)金融資産。

長(cháng)期資本管理(lǐ)公司的(de)投資策略基于市場(chǎng)的(de)有效性，認爲資本市場(chǎng)不合理(lǐ)的(de)債券利差會逐漸減小，可(kě)以通(tōng)過買入低估資産/賣出高(gāo)估資産賺取這(zhè)部分(fēn)利差。他(tā)們通(tōng)過對(duì)大(dà)量曆史數據的(de)測算(suàn)，認爲可(kě)以通(tōng)過對(duì)債券投資進行嚴格對(duì)沖，保證一個(gè)極低的(de)風險暴露。在執行層面，他(tā)們通(tōng)過精确的(de)電腦(nǎo)自動數學模型發現衆多(duō)寶貴的(de)債券利差投資機會，并通(tōng)過向同業金融機構融資，運用(yòng)巨大(dà)的(de)财務杠杆來(lái)放大(dà)收益。

1998 年初，亞洲金融危機爆發後低信用(yòng)等級國債相較歐美(měi)國債利差顯著擴大(dà)。經過模型計算(suàn)，長(cháng)期資本管理(lǐ)公司的(de)交易員(yuán)相信互換利率交易利差會逐漸回縮。所以，他(tā)們動用(yòng)大(dà)量資金抛空互換利率交易利差。1998 年 8 月(yuè)，俄羅斯金融危機爆發，俄羅斯違背了(le)承諾拒絕償付債款并任由盧布貶值；國際炒家和(hé)投資者紛紛撤資，從各種低信用(yòng)等級債券中倉皇出逃，而這(zhè)些撤出的(de)資金唯一目的(de)地就是風險較低的(de)歐美(měi)國家債券。所以，美(měi)國短期債券和(hé) 30 年長(cháng)期債券利率大(dà)幅下(xià)調，長(cháng)期資本公司持有的(de)大(dà)量俄羅斯債券以及各種低信用(yòng)國債利率火箭攀升，二者之間的(de)利差并未如預期縮小而是進一步顯著放大(dà)，高(gāo)杠杆下(xià)産生的(de)虧損驚人(rén)，長(cháng)期資本管理(lǐ)公司的(de)淨資産 1 個(gè)多(duō)月(yuè)時(shí)間縮水(shuǐ) 60%，被迫被美(měi)林(lín)、摩根出資收購(gòu)接管，并于 2000 年徹底倒閉清算(suàn)。這(zhè)個(gè)教訓是對(duì)均值回歸“風險無限”最好的(de)诠釋。

5 正确認知

盡管具有“收益有限、風險無限”的(de)特性，但均值回歸策略仍然在量化(huà)投資中占據著(zhe)一席之地。如何來(lái)正确的(de)看待它的(de)優缺點呢(ne)？首先，随著(zhe)層出不窮的(de)金融工具，越來(lái)越多(duō)的(de)投資品的(de)線性組合将會滿足均值回歸特性。滿足協整的(de)投資品都存在某種基本面的(de)原因，比如上面的(de) EWA 和(hé) EWC，又比如 GDX 和(hé) GLD —— 前者是跟蹤金礦開采公司而後者跟蹤黃(huáng)金。諸如此類的(de)例子還(hái)有很多(duō)。此外，均值回歸策略在投資的(de)頻(pín)率和(hé)周期上非常靈活。我們既可(kě)以在高(gāo)頻(pín)交易中找到價格的(de)背離而運用(yòng)均值回歸策略，又可(kě)以在低頻(pín)的(de)價值投資中找到價格偏離基本面價值的(de)公司來(lái)進行投資（價格最終會回歸到基本面價值）。因此均值回歸策略的(de)适用(yòng)面非常廣泛。另一方面，均值回歸和(hé)主流的(de)趨勢追蹤策略有很高(gāo)的(de)互補性。同時(shí)使用(yòng)的(de)話(huà)可(kě)以提高(gāo)一個(gè)投資組合的(de)夏普率。這(zhè)些都是均值回歸策略的(de)優點。

而缺點方面，就如同上面長(cháng)期資本的(de)例子。誰也(yě)不知道基本面原因是否會突然失效。舉個(gè)例子，GDX 和(hé) GLD 的(de)價差在 2008 年突然失效，後來(lái)得(de)知是因爲能源價格的(de)蹿升（金礦開采需要大(dà)量能源）。因此，如果沒有做(zuò)好風控而依然等著(zhe)價差回歸的(de)話(huà)可(kě)能會因此而死的(de)很慘。後續研究發現，GDX、GLD 和(hé)油價三者從那之後可(kě)以構建出滿足協整的(de)線性組合。再有就是當一個(gè)均值回歸策略讓使用(yòng)者嘗到甜頭之後，因爲其較高(gāo)的(de)夏普率，投資者往往會變得(de)非常大(dà)膽從而不自覺的(de)加大(dà)杠杆。這(zhè)無疑相當于身上随時(shí)綁著(zhe)一顆雷。一旦價格未按預想的(de)回歸，則有可(kě)能在很短的(de)時(shí)間内産生巨大(dà)的(de)虧損。

最後來(lái)看看均值回歸策略都有哪些應用(yòng)場(chǎng)景：

這(zhè)些巨大(dà)的(de)應用(yòng)前景維持著(zhe)均值回歸策略旺盛的(de)生命力；任何一個(gè)量化(huà)投資團隊都無法對(duì)它視而不見。

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。