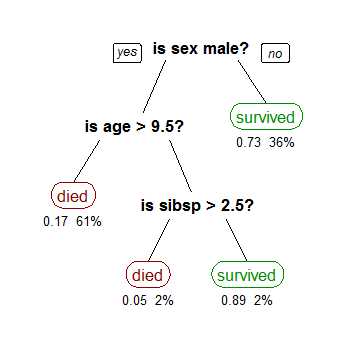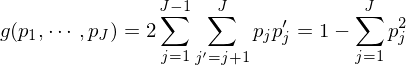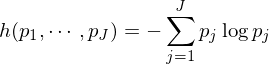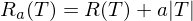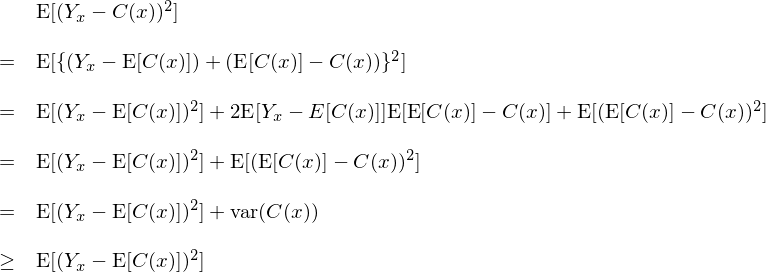“少樹”服從“多(duō)樹”（上）

作者：石川

摘要：分(fēn)類樹算(suàn)法能處理(lǐ)大(dà)量樣本和(hé)大(dà)量特征數據，但單一分(fēn)類樹存在固有的(de)方差，影(yǐng)響了(le)其準确性。

1 引言

機器學習(xí)（machine learning）和(hé)投資的(de)結合點之一便是選股。對(duì)于機器學習(xí)來(lái)說，選股可(kě)被視爲一個(gè)分(fēn)類（classification）問題。與股票(piào)相關的(de)各種估值、财務和(hé)技術等因子都可(kě)以看作是用(yòng)來(lái)對(duì)股票(piào)分(fēn)類的(de)特征（feature），而股票(piào)的(de)漲跌幅則決定股票(piào)屬于哪一類（比如好的(de)股票(piào)和(hé)差的(de)股票(piào)）。用(yòng)機器學習(xí)進行選股屬于監督學習(xí)（supervised learning），它将好的(de)和(hé)差的(de)股票(piào)進行标記（labeling），然後讓某種分(fēn)類算(suàn)法使用(yòng)曆史數據訓練、學習(xí)并挖掘股票(piào)收益率和(hé)股票(piào)特征之間的(de)關系，從而形成一個(gè)分(fēn)類模型。得(de)到分(fēn)類模型後，每當有新一期的(de)特征數據之後，便可(kě)以使用(yòng)該模型對(duì)股票(piào)進行分(fēn)類，選出在下(xià)一個(gè)投資周期内收益率（在概率上）會更加優秀的(de)股票(piào)。這(zhè)便是機器學習(xí)選股的(de)過程。在這(zhè)個(gè)過程中，分(fēn)類算(suàn)法是一個(gè)選股成功與否的(de)核心之一。

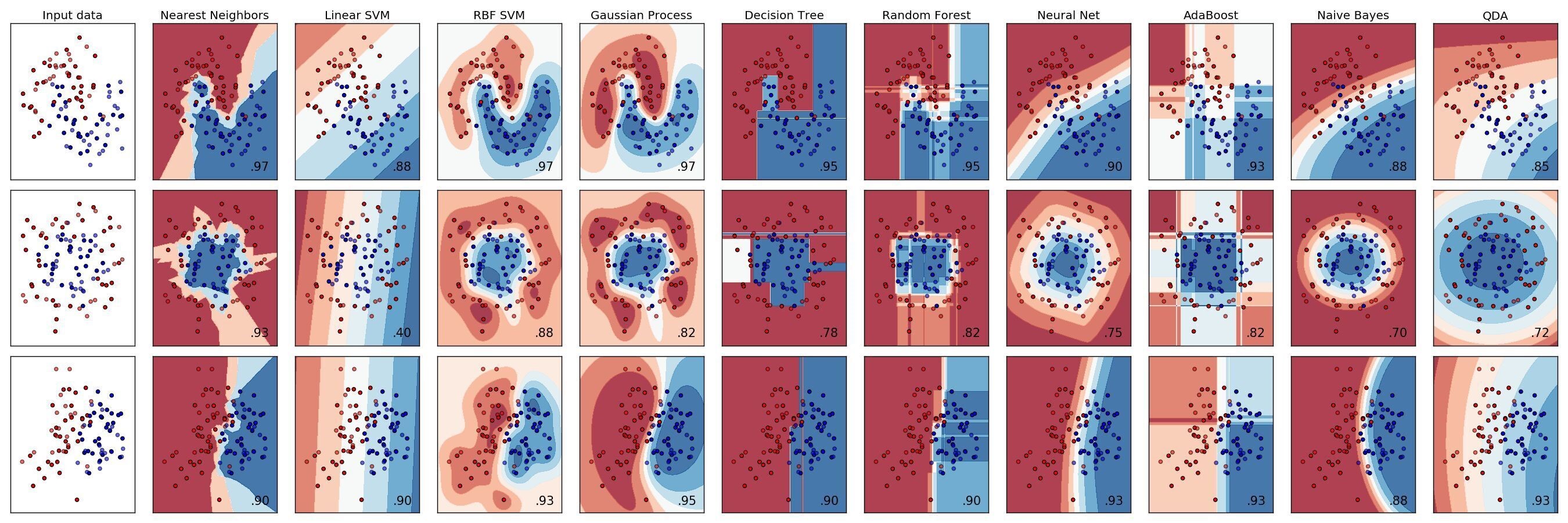
成熟的(de)監督學習(xí)的(de)分(fēn)類算(suàn)法包括支持向量機（support vector machines），樸素貝葉斯（naïve Bayes），最近鄰居法（K nearest neighbors），神經網絡（neural nets），以及分(fēn)類樹（classification trees 又稱 decision trees）及其發展出來(lái)的(de)一系列高(gāo)級算(suàn)法等等。下(xià)圖爲一些主流分(fēn)類算(suàn)法在三個(gè)不同的(de)數據集上的(de)分(fēn)類效果。

在今天和(hé)下(xià)期的(de)量化(huà)核武研究中，我們分(fēn)兩期聊聊分(fēn)類樹的(de)相關算(suàn)法，這(zhè)包括基礎的(de)分(fēn)類樹，以及可(kě)以顯著提升其分(fēn)類效果的(de)高(gāo)級算(suàn)法，包括裝袋算(suàn)法（bagging）、提升算(suàn)法（boosting）、以及随機森林(lín)（random forest）。這(zhè)些高(gāo)級算(suàn)法與基礎分(fēn)類樹的(de)本質區(qū)别是它們使用(yòng)了(le)許多(duō)個(gè)分(fēn)類樹（而非單一分(fēn)類樹），然後再把這(zhè)些多(duō)個(gè)分(fēn)類樹的(de)分(fēn)類結果按某種權重平均，作爲最終的(de)分(fēn)類結果。Bagging，Boosting 以及 Random Forest 都屬于集成學習(xí)（ensemble learning），它們通(tōng)過使用(yòng)和(hé)結合多(duō)個(gè)單一分(fēn)類樹來(lái)取得(de)更優秀的(de)分(fēn)類效果。因此，形象的(de)說，單一分(fēn)類樹是一棵樹，而這(zhè)些高(gāo)級算(suàn)法則使用(yòng)了(le)整片森林(lín)（許多(duō)許多(duō)的(de)單一分(fēn)類樹組成了(le)森林(lín)）。

在本期中，我們首先介紹單一分(fēn)類樹算(suàn)法和(hé)它的(de)一些問題。

2 分(fēn)類樹和(hé) CART 算(suàn)法

2.1 認識分(fēn)類樹

一個(gè)典型的(de)分(fēn)類問題可(kě)以描述如下(xià)：

分(fēn)類器之所以爲監督學習(xí)，是因爲它的(de)參數的(de)選擇依賴于基于曆史數據的(de)學習(xí)。這(zhè)是因爲人(rén)們相信過去的(de)經驗可(kě)以指導未來(lái)的(de)分(fēn)類。因此，在訓練分(fēn)類器的(de)時(shí)候，所有的(de)曆史樣本的(de)正确類别是已知的(de)，它們和(hé)樣本的(de)特征一起作爲分(fēn)類器的(de)輸入，分(fēn)類器通(tōng)過學習(xí)這(zhè)些數據按照(zhào)一定的(de)損失函數（loss function）來(lái)決定分(fēn)類器的(de)參數。

一個(gè)分(fēn)類樹以所有的(de)樣本爲待分(fēn)類的(de)起點，通(tōng)過重複分(fēn)裂（repetitive splits）将所有樣本分(fēn)成不同的(de)子集。在每一次分(fēn)裂時(shí)，以一個(gè)或多(duō)個(gè)特征的(de)線性組合作爲分(fēn)類的(de)依據、逐層分(fēn)類，每層都在上一層分(fēn)類的(de)結果上選取新的(de)分(fēn)類屬性進一步細分(fēn)樣本，從而形成一種發散式的(de)樹狀遞階結構（hierarchical structure）。

下(xià)圖是 wiki 上面一個(gè)用(yòng)泰坦尼克号幸存者數據建模的(de)分(fēn)類樹模型（輸入數據爲所有乘客的(de)人(rén)口特征，類别爲幸存和(hé)死亡兩類）。圖中，黑(hēi)色粗體節點說明(míng)每一層級選用(yòng)的(de)分(fēn)類特征，比如第一層分(fēn)類時(shí)選用(yòng)了(le)性别（它的(de)兩個(gè)分(fēn)支爲男(nán)性和(hé)女(nǚ)性），第二層分(fēn)類時(shí)選用(yòng)了(le)年齡（它的(de)兩個(gè)分(fēn)支爲年齡超過 9.5 歲與否），第三層分(fēn)類時(shí)選用(yòng)了(le)同船的(de)配偶及兄弟(dì)姐妹個(gè)數（它的(de)兩個(gè)分(fēn)支爲該個(gè)數是否大(dà)于 2.5）。這(zhè)些分(fēn)類節點在這(zhè)個(gè)分(fēn)類樹中被稱爲内部節點。而圖中紅色和(hé)綠色的(de)圓角矩形則代表了(le)這(zhè)顆分(fēn)類樹末端的(de)樹葉（leaf）；每片樹葉都被标有一個(gè)明(míng)确的(de)類别（本例中的(de)幸存或者死亡）。分(fēn)類樹一旦确定，它的(de)内部分(fēn)類節點便清晰的(de)說明(míng)了(le)它的(de)分(fēn)類過程。在本例中，不難看出婦女(nǚ)和(hé)兒(ér)童是泰塔尼克沉船時(shí)的(de)主要幸存者，這(zhè)和(hé)實際情況是相符的(de)。

本例雖然簡單，但它說明(míng)分(fēn)類樹算(suàn)法的(de)兩個(gè)重要的(de)問題：

以上兩點說明(míng)，一個(gè)分(fēn)類樹模型是否優秀取決于兩點：如何選取有效的(de)分(fēn)類特征，以及如何确定分(fēn)類樹的(de)大(dà)小（分(fēn)的(de)類太粗可(kě)能造成特征的(de)不充分(fēn)利用(yòng)，分(fēn)的(de)類太細則造成過拟合）。下(xià)面就簡要介紹确定分(fēn)類樹模型的(de) CART 算(suàn)法。

2.2 CART 算(suàn)法

CART 是 Classification And Regression Trees 的(de)縮寫，由 Breiman et al. (1984) 發明(míng)，自發明(míng)以來(lái)得(de)到了(le)長(cháng)足的(de)發展，成爲了(le)商業化(huà)的(de)分(fēn)類樹算(suàn)法軟件。它可(kě)以根據給定的(de)曆史數據和(hé)評價标準來(lái)決定分(fēn)類樹模型（即選擇各層的(de)分(fēn)類特征并确定分(fēn)類樹的(de)大(dà)小）。在确定分(fēn)類樹時(shí)，CART 算(suàn)法考慮如下(xià)幾個(gè)問題：（1）如何選擇當前層的(de)分(fēn)類特征；（2）如何評價分(fēn)類樹的(de)分(fēn)類準确性；（3）如何通(tōng)過綜合考慮分(fēn)類準确性和(hé)複雜(zá)程度來(lái)決定分(fēn)類樹的(de)大(dà)小。下(xià)面逐一說明(míng)。

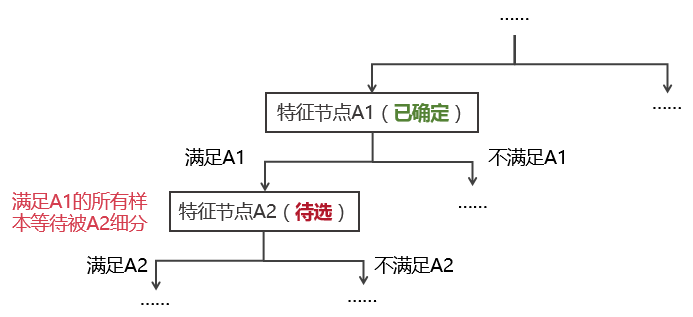
選擇當前層的(de)分(fēn)類特征：CART 是一個(gè)遞歸式的(de)二元分(fēn)類法：對(duì)于每一個(gè)特征，待分(fēn)配的(de)樣本按照(zhào)是否滿足該特征被分(fēn)爲兩類。下(xià)圖說明(míng) CART 算(suàn)法如何選擇每一層的(de)分(fēn)類特征。假設在遞歸過程中，算(suàn)法在上一步叠代中已經确定了(le)特征節點 A1，讓我們來(lái)考慮如何進一步選擇特征 A2 來(lái)細分(fēn)所有滿足 A1 的(de)樣本。

在确定特征節點 A2 的(de)時(shí)候，待分(fēn)類樣本包含的(de)所有特征都會被考慮。在所有特征中，“分(fēn)類效果最好”的(de)那個(gè)特征将被選爲 A2。那麽如何定義“分(fēn)類效果最好”呢(ne)？這(zhè)可(kě)以由節點的(de)純度（purity）來(lái)定義。爲此，定義一個(gè)衡量節點分(fēn)類純度的(de)雜(zá)質方程（impurity function）。以特征節點 A1 爲例，假設滿足該節點的(de)樣本中，屬于第 i 類的(de)樣本個(gè)數爲 Pi，i = 1, …, m。因此，A1 節點的(de)雜(zá)質方程可(kě)以由 Gini 多(duō)樣性指數（Gini index of diversity）或者熵函數（entropy function）來(lái)定義。它們都是 Pi 的(de)函數。

Gini 多(duō)樣性指數：

熵函數：

理(lǐ)想狀态下(xià)，如果所有滿足 A1 的(de)樣本都屬于同一類，記爲 i*，那麽僅當 i = i* 時(shí)有 Pi = 1, 其他(tā)的(de) Pi = 0。在這(zhè)種情況下(xià)，上述兩個(gè)雜(zá)質函數的(de)取值都是 0，說明(míng)節點的(de)純度爲 1。在一般情況下(xià)，由于滿足該節點的(de)樣本不可(kě)能都屬于同一類，因此雜(zá)質函數的(de)取值大(dà)于 0（節點純度小于 1）。

有了(le)分(fēn)類好壞的(de)評價标準，我們就可(kě)以選擇分(fēn)類特征 A2 了(le)。對(duì)于每一個(gè)候選特征，計算(suàn)按其分(fēn)類後細分(fēn)出來(lái)的(de)兩個(gè)節點（即滿足該特征的(de)節點和(hé)不滿足該特征的(de)節點）的(de)純度的(de)加權平均（可(kě)以按照(zhào)樣本個(gè)數加權）。用(yòng)這(zhè)個(gè)純度減去 A1 節點的(de)純度就是該候選特征的(de)分(fēn)類效果。在所有候選特征中，能夠最大(dà)限度提升分(fēn)類純度的(de)節點被選爲 A2。值得(de)一提的(de)時(shí)，這(zhè)個(gè)選擇節點的(de)方法隻考慮了(le)當前分(fēn)類的(de)局部最優，即選出的(de) A2 是在當前情況下(xià)能最大(dà)化(huà)提升分(fēn)類純度的(de)特征；A2 的(de)選擇是不考慮後續可(kě)能的(de)分(fēn)類的(de)。因此，CART 算(suàn)法在選擇分(fēn)類特征時(shí)是一種貪心法（greedy algorithm）。

評價分(fēn)類樹的(de)準确性：和(hé)所有機器學習(xí)算(suàn)法一樣，我們關心的(de)是得(de)到的(de)分(fēn)類樹對(duì)未來(lái)新樣本的(de)分(fēn)類效果。因此，在評估分(fēn)類樹的(de)準确性時(shí)，考慮該模型在訓練數據（即用(yòng)來(lái)建模的(de)數據）上的(de)效果是沒有意義的(de)。這(zhè)是因爲在極端過拟合的(de)情況下(xià)，模型在訓練集上的(de)誤差可(kě)以降爲 0。對(duì)于分(fēn)類樹來(lái)說，如果每一個(gè)單一樣本都通(tōng)過它獨有的(de)特征取值被分(fēn)到一個(gè)單一的(de)末端樹葉上，那麽這(zhè)個(gè)模型便可(kě)以 100% 正确地對(duì)訓練集分(fēn)類，但這(zhè)樣“準确性”對(duì)于我們評估該分(fēn)類樹對(duì)未來(lái)新數據的(de)分(fēn)類效果毫無幫助。

因此，在評判分(fēn)類效果時(shí)，理(lǐ)想的(de)狀态是用(yòng)在訓練時(shí)沒有使用(yòng)過的(de)數據，我們稱之爲測試集。測試集中的(de)樣本來(lái)自與訓練集樣本同樣的(de)本體（population）、符合同樣的(de)分(fēn)布。因此，如果我們有足夠多(duō)的(de)數據，那麽使用(yòng)額外的(de)測試集是最佳的(de)選擇。但是在很多(duō)情況下(xià)，尤其是金融領域，數據是稀缺和(hé)寶貴的(de)。對(duì)于選股，我們希望盡可(kě)能多(duō)的(de)使用(yòng)曆史數據來(lái)訓練模型。在這(zhè)種情況下(xià)，爲了(le)确保模型評價的(de)正确性，可(kě)以采用(yòng) K 折交叉驗證的(de)方法（K-fold cross validation）。

K 折交叉驗證将訓練集分(fēn)爲 K 等分(fēn)，每次将第 i 份（i = 1, …, K）的(de)數據留作驗證之用(yòng)，而用(yòng)剩餘的(de) K-1 份數據建模得(de)到一個(gè)分(fēn)類樹，然後将該模型對(duì)第 i 份數據進行分(fēn)類，用(yòng)分(fēn)類的(de)誤差評估該模型的(de)分(fēn)類能力。對(duì)每份數據重複上面的(de)操作便得(de)到 K 個(gè)分(fēn)類樹模型（在實際中，K 的(de)取值一般爲 5 到 10 之間）。在建立這(zhè) K 個(gè)分(fēn)類樹時(shí)，應保證建模的(de)标準是相同的(de)（比如它們的(de)雜(zá)質方程應該是相同的(de)，不能有些使用(yòng) Gini 多(duō)樣性指數，而另一些使用(yòng)熵函數；又或者如果在建模時(shí)指定了(le)分(fēn)類樹末端樹葉的(de)個(gè)數，那麽這(zhè) K 棵樹必須有相同的(de)樹葉個(gè)數）。把這(zhè) K 個(gè)分(fēn)類樹各自的(de)誤差取平均便得(de)到了(le)一個(gè)加權平均。如果我們用(yòng)該建模标準對(duì)原始的(de)所有訓練樣本數據進行建模，那麽上述這(zhè)個(gè)加權平均就是該模型誤差的(de)估計。

确定分(fēn)類樹的(de)大(dà)小：在生成一顆分(fēn)類樹時(shí)，很難有一個(gè)有效的(de)停止分(fēn)裂标準（stop splitting rule）來(lái)決定不再繼續細分(fēn)。這(zhè)是因爲在分(fēn)類樹的(de)發展中，可(kě)能出現這(zhè)種情況，即當前這(zhè)一步的(de)分(fēn)類隻有限的(de)提升分(fēn)類效果，但接下(xià)來(lái)的(de)分(fēn)類卻能很大(dà)的(de)提升分(fēn)類效果。在這(zhè)種情況下(xià)，基于當前有限的(de)分(fēn)類提升效果而停止繼續分(fēn)類則是錯誤的(de)。

在這(zhè)個(gè)背景下(xià)，正确的(de)做(zuò)法是先生成一顆足夠大(dà)的(de)分(fēn)類樹（比如要求每個(gè)末端樹葉下(xià)不超過 5 個(gè)樣本），記爲 T0。通(tōng)過對(duì)這(zhè)顆分(fēn)類樹進行“剪枝”（pruning）來(lái)确定它的(de)最佳尺寸。在修剪時(shí)，會綜合考慮分(fēn)類的(de)誤差和(hé)分(fēn)類樹的(de)複雜(zá)程度，因而采用(yòng)了(le)成本及複雜(zá)性綜合最小化(huà)的(de)剪枝（minimum cost–complexity pruning）。

假設我們有一顆分(fēn)類樹 T，它的(de)末端樹葉的(de)個(gè)數記爲 |T|，它的(de)分(fēn)類誤差爲 R(T)。另外，非負實數 a 爲分(fēn)類樹複雜(zá)度的(de)懲罰系數。如果用(yòng) Ra(T) 表示綜合評價準确性和(hé)複雜(zá)性的(de)測度，則有：

由于 a 是複雜(zá)度的(de)懲罰系數，當 a 很小時(shí)，分(fēn)類樹的(de)準确性會優先于複雜(zá)度，因此得(de)到的(de)分(fēn)類樹會有較多(duō)的(de)枝節和(hé)末端樹葉、分(fēn)類誤差較低；随著(zhe) a 的(de)增大(dà)，對(duì)複雜(zá)度的(de)厭惡程度加大(dà)，分(fēn)類樹的(de)複雜(zá)度會降低，擁有較少的(de)枝節和(hé)末端樹葉、但分(fēn)類誤差也(yě)會增加。因此，我們希望通(tōng)過搜索來(lái)找到最優的(de) a 使得(de) Ra(T) 最小。當 Ra(T) 最小時(shí)對(duì)應的(de)分(fēn)類樹就是最優的(de)分(fēn)類樹。

爲了(le)找到最優的(de)分(fēn)類樹，算(suàn)法會從最初的(de)分(fēn)類樹 T0 開始，對(duì)于不同的(de) a 的(de)取值（由小到大(dà)，單調遞增），按照(zhào)最弱環節切割（weakest-link cutting）法生成一系列的(de)嵌套樹（nested trees）T1，T2，……。由于修剪會減少分(fēn)類樹的(de)節點，從而造成其分(fēn)類效果下(xià)降，而修剪不同節點對(duì)分(fēn)類效果的(de)負面影(yǐng)響是不同的(de)。因此，最弱環節切割的(de)意思就是在修剪分(fēn)類樹的(de)節點時(shí)，應該剪掉對(duì)分(fēn)類效果負面影(yǐng)響最小的(de)節點。（有興趣的(de)讀者請進一步參閱 Sutton 2005）。

所謂嵌套樹，就是說 T1 是由修剪 T0 的(de)枝幹和(hé)節點得(de)到，T2 是由修剪 T1 得(de)到，每一棵樹都由修剪之前一棵樹得(de)到。舉例來(lái)說，假如我們在 1 到 10 之間的(de)整數中尋找最優的(de) a：首先取 a = 1，并由 T0 開始生成一顆新的(de)分(fēn)類樹 T1 使得(de) R1(T1) 最小；然後取 a = 2，并由 T1 開始生成一顆新的(de)分(fēn)類樹 T2 使得(de) R2(T2) 最小；以此類推，最終我們會從分(fēn)類樹 T9 和(hé) a = 10 生成最後一顆分(fēn)類樹 T10，使得(de) R10(T10) 最小。這(zhè)樣便得(de)到了(le)從 T1 開始到 T10 的(de)一族嵌套樹，而之中的(de)每一顆數之于它對(duì)應的(de) a 來(lái)說都是最優的(de)。最後，比較這(zhè) 10 個(gè)不同的(de) a 的(de)取值，找到使 Ra(Ta) 最小的(de)那個(gè) a。其對(duì)應的(de)分(fēn)類樹 Ta 就是最優的(de)。

綜上所述，假設我們使用(yòng)交叉驗證來(lái)計算(suàn)分(fēn)類樹 T 的(de)準确性的(de)話(huà)，那麽确定最優分(fēn)類樹大(dà)小的(de)步驟爲：

1. 将訓練集樣本分(fēn)成 K 份；

2. 對(duì)于每一份，重複下(xià)面的(de)步驟：

    2.1 将這(zhè)份數據留作驗證之用(yòng)；

    2.2 用(yòng)其他(tā) K-1 份數據建模，得(de)到一顆初始的(de)足夠大(dà)的(de)分(fēn)類樹 T；

    2.3 以 T 爲起點，對(duì)于給定範圍的(de) a，通(tōng)過 minimum cost–complexity pruning 得(de)到一族嵌套的(de)分(fēn)類樹；

3. 經過步驟 2 之後，對(duì)于每一個(gè)給定的(de) a，我們都有 K 顆不同的(de)分(fēn)類樹，将它們的(de) Ra 取平均作爲在整體訓練集上使用(yòng) a 進行修剪後得(de)到的(de)最優分(fēn)類樹的(de)分(fēn)類效果的(de)估計；記使得(de) Ra 平均取最小的(de)那個(gè) a 爲 a*，它就是對(duì)于整體訓練集最優的(de) a；

4. 将訓練集的(de)所有樣本爲對(duì)象，以 a=a* 訓練并修建出一顆分(fēn)類樹，這(zhè)就是我們的(de)最優分(fēn)類樹。

3 分(fēn)類樹的(de)特點和(hé)不足

分(fēn)類樹是一種非參數化(huà)的(de)計算(suàn)密集型算(suàn)法。但是随著(zhe)計算(suàn)機技術的(de)發展，計算(suàn)強度已不再是一個(gè)太大(dà)的(de)問題。這(zhè)種分(fēn)類算(suàn)法可(kě)以處理(lǐ)大(dà)量的(de)樣本以及大(dà)量的(de)特征，有效的(de)挖掘出特征之間的(de)相互作用(yòng)。此外，分(fēn)類樹的(de)解釋性也(yě)比較強，對(duì)特征數據也(yě)沒有獨立性要求，這(zhè)些使它得(de)到了(le)廣泛的(de)應用(yòng)。

然而（單顆）分(fēn)類樹存在一些先天的(de)不足。假設 x 代表樣本點特征（它的(de)取值來(lái)自一個(gè)未知的(de)概率分(fēn)布），Yx 爲該樣本點的(de)真實分(fēn)類，C(x) 爲某分(fēn)類樹對(duì) x 的(de)預測結果（因此 C(x) 是一個(gè)随機變量）。令 E[C(x)] 爲 C(x) 的(de)期望。因此，這(zhè)個(gè)分(fēn)類樹的(de)分(fēn)類誤差滿足：

可(kě)見，分(fēn)類器的(de)誤差分(fēn)爲偏差 E[(Yx – E[C(x)])^2] 和(hé)方差 Var(C(x)) 兩個(gè)部分(fēn)。分(fēn)類樹是一個(gè)不太穩定的(de)分(fēn)類器；當訓練樣本稍有改變時(shí)，分(fēn)類樹的(de)分(fēn)類節點可(kě)能會發生變化(huà)從而造成不同的(de)分(fēn)類結果。這(zhè)意味著(zhe)對(duì)于分(fēn)類樹來(lái)說，Var(C(x)) 不可(kě)忽視，即單一分(fēn)類樹自身的(de)方差對(duì)分(fēn)類誤差的(de)貢獻是固有的(de)。如果我們能夠使用(yòng) E[C(x)] 代替 C(x) 則可(kě)以避免單一分(fēn)類樹自身的(de)方差産生的(de)分(fēn)類誤差。

當然，在實際中，E[C(x)] 是未知的(de)，但是我們可(kě)以通(tōng)過平均大(dà)量不同單顆分(fēn)類樹的(de)分(fēn)類結果來(lái)近似得(de)到 E[C(x)]，使它們各自的(de)方差相互抵消。根據大(dà)數定理(lǐ)，大(dà)量不同分(fēn)類樹的(de)平均結果将有效的(de)逼近 E[C(x)]。這(zhè)便是“少樹”服從“多(duō)樹”帶來(lái)的(de)優勢。

本文第一節提到的(de) bagging（Breiman 1996a, 1996b），boosting（Freund and Schapire 1996），以及随機森林(lín)（Breiman 2001）等算(suàn)法都是使用(yòng)了(le)大(dà)量多(duō)顆分(fēn)類樹取代單一分(fēn)類樹對(duì)數據進行分(fēn)類的(de)經典算(suàn)法。它們在不改變偏差的(de)前提下(xià)有效的(de)降低了(le)分(fēn)類樹自身的(de)方差，從而顯著提高(gāo)了(le)分(fēn)類準确性。我們将在本篇的(de)下(xià)期中介紹這(zhè)些高(gāo)級算(suàn)法。

參考文獻

Breiman, L. (1996a). Bagging predictors. Machine Learning 24, 123 – 140.

Breiman, L. (1996b). Heuristics of instability and stabilization in model selection. Ann. Statist. 24, 2350 – 2383.

Breiman, L. (2001). Random forests. Machine Learning 45, 5 – 32.

Breiman, L., Friedman, J.H., Olshen, R.A., Stone, C.J. (1984). Classification and Regression Trees. Wadsworth, Pacific Grove, CA.

Freund, Y., Schapire, R. (1996). Experiments with a new boosting algorithm. In: Saitta, L. (Ed.), Machine Learning: Proceedings of the Thirteenth International Conference. Morgan Kaufmann, San Francisco, CA.

Sutton, C. D. (2005). Classification and Regression Trees, Bagging, and Boosting. In Rao, C. R., Wegman, E. J., Solka, J. L. (Eds.), Handbook of Statistics 24: Data Mining and Data Visualization, Chapter 11.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。