“少樹”服從“多(duō)樹”（下(xià)）

作者：石川

摘要：裝袋法、随機森林(lín)以及提升法是三種有效的(de)集合學習(xí)元算(suàn)法。它們可(kě)以提高(gāo)分(fēn)類樹的(de)分(fēn)類準确性。

1 前文回顧

前篇《“少樹”服從“多(duō)樹”（上）》中系統介紹了(le)單顆分(fēn)類樹算(suàn)法。同時(shí)，我們指出分(fēn)類樹算(suàn)法不夠穩定，對(duì)訓練樣本數據比較敏感，造成其固有的(de)方差，而方差又是預測誤差的(de)原因之一。爲了(le)有效降低方差，使用(yòng)多(duō)顆分(fēn)類樹然後平均它們的(de)結果作爲最終的(de)結果便成爲一種自然的(de)選擇。在這(zhè)方面，裝袋算(suàn)法（bagging）、提升算(suàn)法（boosting）、随機森林(lín)（random forest）都是很好的(de)方法。它們都是機器學習(xí)領域的(de)集成學習(xí)元算(suàn)法（ensemble learning meta algorithm）。元算(suàn)法的(de)意思是算(suàn)法的(de)算(suàn)法；如果說算(suàn)法的(de)作用(yòng)對(duì)象是數據，那麽元算(suàn)法的(de)作用(yòng)對(duì)象就是算(suàn)法。它們可(kě)以理(lǐ)解爲一種作用(yòng)于基礎分(fēn)類算(suàn)法上的(de)技術，以取得(de)更佳的(de)分(fēn)類效果。

本期就分(fēn)别介紹并比較這(zhè)三種技術。爲了(le)更好的(de)介紹它們，首先來(lái)看一個(gè)名爲自助抽樣法的(de)概念。

2 自助抽樣法

有放回的(de)的(de)重采樣：自助抽樣法（bootstrapping）是指從給定的(de)數據集中有放回的(de)重采樣（resampling with replacement）。在這(zhè)個(gè)定義中，“有放回”是核心。舉個(gè)例子。假設我們有标号 1 到 10 的(de) 10 個(gè)小球，放在一個(gè)袋子裏。下(xià)面我們“有放回”地不斷地從袋子裏随機抽出小球。假設第一次抽取中，我們抽出了(le) 3 号小球，有放回則是說我們在下(xià)一次抽取之前把 3 号小球放回到袋子裏，即在第二次抽取的(de)時(shí)候，我們仍然有可(kě)能再次抽到 3 号小球（它和(hé)其他(tā) 9 個(gè)球被抽到的(de)概率是一樣的(de)），這(zhè)便是有放回的(de)含義。作爲對(duì)比，生活中更多(duō)的(de)是“無放回抽取”，比如體彩 36 中 7 或者歐冠抽簽，抽出的(de)小球都不會再放回池子中。

随機生成大(dà)量不同的(de)樣本：讓我們仍然考慮 10 個(gè)小球這(zhè)個(gè)例子。假設我們有放回的(de)從口袋裏抽取 10 個(gè)球，得(de)到一個(gè)小球序号的(de)序列 3，5，6，1，1，7，9，10，2，6（即 1 号和(hé) 6 号球被取出兩次；4 号和(hé) 8 号球沒有被抽到）。這(zhè)便是一個(gè)重采樣得(de)到的(de)樣本序列。通(tōng)過進行大(dà)量的(de)有放回的(de)重采樣，我們可(kě)以用(yòng)原始的(de)樣本生成許多(duō)不同的(de)新的(de)樣本序列。這(zhè)麽做(zuò)的(de)意義重大(dà)。

自助抽樣的(de)統計學意義：自助抽樣的(de)目的(de)是幫助我們推斷樣本統計量（sample statistic）在估計總體統計量（population statistic）時(shí)的(de)誤差。比如我們想知道全世界所有人(rén)的(de)平均身高(gāo)（這(zhè)個(gè)平均身高(gāo)就是總體統計量，因爲我們考慮的(de)全世界所有人(rén)）。然而，我們不可(kě)能給全世界約 74 億人(rén)都測量身高(gāo)再計算(suàn)平均值。因此，我們隻能對(duì)一小部分(fēn)樣本進行分(fēn)析。假設我們在全世界随機抽取了(le) 5 萬人(rén)、測量了(le)這(zhè)些人(rén)的(de)身高(gāo)，并計算(suàn)出這(zhè) 5 萬人(rén)的(de)平均身高(gāo)爲 1.72 米，這(zhè)便是樣本統計量。當我們用(yòng) 1.72 米作爲全世界總人(rén)口平均身高(gāo)的(de)估計時(shí)，我們無法回答(dá)這(zhè)個(gè)估計是否準确、誤差是多(duō)少。這(zhè)是因爲我們隻有這(zhè)一個(gè) 5 萬人(rén)的(de)樣本；我們沒有更多(duō)的(de)其他(tā)的(de)樣本。這(zhè)時(shí)，有放回的(de)重采樣便可(kě)大(dà)顯身手。

具體的(de)，我們可(kě)以把這(zhè) 5 萬人(rén)看作是原始數據，通(tōng)過進行大(dà)量的(de)有放回重采樣（比如 10000 次），得(de)到足夠多(duō)的(de)樣本大(dà)小爲 5 萬人(rén)的(de)不同的(de)樣本序列。這(zhè)個(gè)分(fēn)析方法的(de)核心和(hé)巧妙之處是：我們暫時(shí)抛開那個(gè)真實的(de)總體（74 億人(rén)），而把這(zhè) 5 萬人(rén)就當作是我們分(fēn)析的(de)“總體”，并把經過有放回重采樣得(de)到的(de) 10000 個(gè)樣本作爲基于這(zhè)個(gè) 5 萬人(rén)“總體”得(de)到的(de)“樣本”。

通(tōng)過計算(suàn)這(zhè) 10000 個(gè)"樣本"的(de)平均身高(gāo)，得(de)到“樣本”平均身高(gāo)的(de)分(fēn)布。由于“總體”就是那 5 萬人(rén)；它的(de)所有統計量都是已知的(de)，因此我們可(kě)以準确地計算(suàn)這(zhè) 10000 個(gè)“樣本”計算(suàn)出的(de)樣本統計量在推斷這(zhè) 5 萬人(rén)“總體”的(de)總體統計量的(de)誤差，記爲 e'。更近一步，不要忘了(le)這(zhè) 5 萬人(rén)其實是從那 74 億人(rén)真實總體得(de)到的(de)一個(gè)真實樣本。令 e 表示用(yòng)這(zhè) 5 萬人(rén)樣本的(de)樣本統計量推斷 74 億人(rén)總體的(de)總體統計量時(shí)的(de)誤差。如果這(zhè) 5 萬人(rén)的(de)概率分(fēn)布是那 74 億人(rén)的(de)概率分(fēn)布的(de)一個(gè)合理(lǐ)的(de)近似，那麽我們就可(kě)以用(yòng) e' 來(lái)估計 e。

3 裝袋算(suàn)法

何爲裝袋算(suàn)法：裝袋算(suàn)法（bagging）由 Breiman (1996a, 1996b) 發明(míng)。Bagging 一詞從英文 Bootstrap aggregating 而來(lái)，中文翻譯爲很拗口的(de)引導聚類算(suàn)法，爲了(le)好記又按 bagging 直譯取名爲裝袋算(suàn)法。爲了(le)理(lǐ)解它的(de)含義，我們不用(yòng)管那個(gè)中文翻譯，隻需要把這(zhè)兩個(gè)單詞拆開來(lái)看：Bootstrap aggregating = Bootstrap + aggregate。前一個(gè)詞就代表了(le)上一節介紹的(de)自助抽樣，而後一個(gè)詞就是聚合之意。它的(de)意思是：

裝袋爲什(shén)麽有效：分(fēn)類樹本身是一種不穩定的(de)分(fēn)類器，對(duì)訓練數據的(de)敏感性比較高(gāo)。訓練數據的(de)特征值的(de)一些細微擾動可(kě)能造成分(fēn)類樹結構的(de)不同，從而使得(de)預測結果不同。這(zhè)使得(de)分(fēn)類樹的(de)預測方差比較大(dà)。一個(gè)分(fēn)類算(suàn)法的(de)預測誤差由偏差和(hé)誤差兩部分(fēn)造成（具體的(de)請參閱 Sutton 2005）。裝袋算(suàn)法通(tōng)過聚合大(dà)量單一分(fēn)類樹可(kě)以有效的(de)減少單一分(fēn)類樹的(de)預測方差。誠然，聚合也(yě)會在一定程度上增加預測偏差，但增加幅度有限，可(kě)以被大(dà)大(dà)減少的(de)方差所抵消。因此，對(duì)于分(fēn)類樹這(zhè)種自身預測偏差較小，但是預測方差較大(dà)的(de)分(fēn)類器來(lái)說，裝袋算(suàn)法可(kě)以非常有效的(de)提高(gāo)其整體的(de)預測準确性。

在實際應用(yòng)中，Hastie et al. (2001) 指出使用(yòng) 50 到 100 個(gè)重采樣的(de)樣本便可(kě)以取得(de)理(lǐ)想的(de)結果（更多(duō)的(de)樣本也(yě)無法明(míng)顯地進一步提升準确性）。上一篇中提到爲了(le)确定分(fēn)類樹的(de)最佳尺寸，需要使用(yòng) K 折交叉驗證，這(zhè)意味著(zhe)找到最優單顆分(fēn)類樹都需要一定的(de)計算(suàn)時(shí)間。然而，當我們采用(yòng)裝袋算(suàn)法時(shí)，可(kě)以避免使用(yòng)交叉驗證。對(duì)于每一棵分(fēn)類樹，我們都可(kě)以使用(yòng)原始的(de)樣本數據作爲測試集來(lái)檢驗其準确性。又或者，我們可(kě)以通(tōng)過計算(suàn)袋外誤差（out-of-bag error）來(lái)計算(suàn)。計算(suàn)袋外誤差時(shí)，對(duì)于訓練樣本中的(de)每一個(gè)點，使用(yòng)所有那些用(yòng)不包含該點的(de)重采樣樣本所訓練出的(de)分(fēn)類樹對(duì)其分(fēn)類（這(zhè)就是袋外的(de)意思），和(hé)該點的(de)實際類别比較看看是否分(fēn)類正确。平均所有樣本點的(de)分(fēn)類正誤便得(de)到袋外誤差。雖然裝袋算(suàn)法要計算(suàn)許多(duō)分(fēn)類樹，但是由于它可(kě)以避免使用(yòng)交叉驗證，因此裝袋算(suàn)法的(de)計算(suàn)時(shí)間仍然是可(kě)接受的(de)。

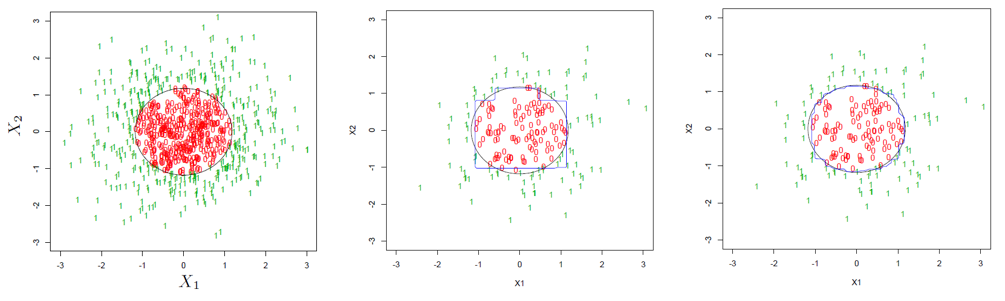
最後用(yòng)下(xià)面這(zhè)個(gè)例子直觀的(de)說明(míng)裝袋法的(de)好處。假設待分(fēn)類的(de)數據是二維平面上的(de)點，每個(gè)點都可(kě)以用(yòng)坐(zuò)标 (x1, x2) 表示。下(xià)圖左一爲所有點表示的(de)總體，0 和(hé) 1 表示每一個(gè)點的(de)分(fēn)類，黑(hēi)色的(de)圓圈表示決策邊界（decision boundary）。假設我們從總體中随機抽出 200 個(gè)點，并用(yòng)它們來(lái)訓練單一分(fēn)類樹，得(de)到的(de)分(fēn)類決策邊界如下(xià)圖中間那副所示。可(kě)以看到該決策邊界和(hé)真實的(de)邊界差别非常明(míng)顯，這(zhè)意味著(zhe)這(zhè)樣一個(gè)分(fēn)類樹的(de)分(fēn)類誤差是非常可(kě)觀的(de)。下(xià)圖右一爲使用(yòng)了(le)裝袋算(suàn)法後的(de)結果。可(kě)以清楚的(de)看到，我們的(de)訓練數據仍然還(hái)是那 200 個(gè)點，但是經過重采樣再聚合，最後得(de)到的(de)決策邊界比單一分(fēn)類樹的(de)決策邊界大(dà)大(dà)平滑了(le)，更加貼近真實的(de)決策邊界，顯著提升了(le)分(fēn)類準确性。

4 随機森林(lín)

随機森林(lín)（random forests）由 Breiman (2001) 提出，它和(hé)裝袋算(suàn)法非常類似，是裝袋算(suàn)法的(de)進階版。由前述可(kě)知，由于考慮了(le)很多(duō)分(fēn)類樹，裝袋算(suàn)法本身已經是“森林(lín)”了(le)。因此，随機森林(lín)和(hé)裝袋算(suàn)法的(de)唯一差别就在“随機”兩個(gè)字上。

在裝袋法中，不同的(de)樣本集都是通(tōng)過對(duì)原始數據重采樣得(de)到的(de)。因此，這(zhè)些樣本集——雖然它們之間有一定的(de)差異——仍然是有很高(gāo)的(de)相關性的(de)。在提出随機森林(lín)的(de)時(shí)候，Breiman 證明(míng)了(le)裝袋算(suàn)法的(de)分(fēn)類誤差的(de)上限是和(hé)樣本集之間的(de)相關性有關的(de)。隻有想辦法降低樣本集之間的(de)相關性，才能進一步提高(gāo)裝袋法的(de)效果。因此，他(tā)提出引入随機性。

具體的(de)，随機森林(lín)算(suàn)法在通(tōng)過重采樣構造大(dà)量樣本集時(shí)和(hé)裝袋算(suàn)法并無差異。但是，在基于每個(gè)樣本集訓練分(fēn)類樹時(shí)，随機森林(lín)算(suàn)法在分(fēn)類特征選擇時(shí)引入了(le)随機性。該算(suàn)法在選擇當前的(de)分(fēn)類特征時(shí)，從所有的(de)候選特征中先随機選出一個(gè)子集，然後再從該子集中選擇出最好的(de)分(fēn)類特征。如果說裝袋法僅僅考慮了(le)樣本的(de)随機性，那麽随機森林(lín)既考慮了(le)樣本随機性又考慮了(le)特征随機性，從而降低了(le)不同分(fēn)類樹之間的(de)相關性。

5 提升算(suàn)法

提升算(suàn)法（boosting）的(de)出發點是想回答(dá)這(zhè)樣一個(gè)問題，即一組“弱學習(xí)者”（week learners）能否通(tōng)過集合學習(xí)生成一個(gè)“強學習(xí)者”（strong learner）？弱學習(xí)者一般是但不限于一個(gè)分(fēn)類效果隻比随機分(fēn)類強一點點的(de)分(fēn)類器（因此單一分(fēn)類樹——雖然它有不錯的(de)分(fēn)類效果——仍然也(yě)可(kě)以在作爲弱學習(xí)者）；強學習(xí)者指分(fēn)類器的(de)結果非常接近真值。因爲算(suàn)法把弱學習(xí)者變成強學習(xí)者，故得(de)名提升算(suàn)法。

Freund and Schapire (1996) 提出了(le) AdaBoost 算(suàn)法，用(yòng)于提升分(fēn)類器的(de)效果。它通(tōng)過叠代，不斷地對(duì)原始樣本數據進行有權重的(de)分(fēn)類。在叠代中的(de)每一步中，樣本點的(de)權重由上一步分(fēn)類器的(de)分(fēn)類誤差計算(suàn)得(de)到。因此，該算(suàn)法在每次叠代時(shí)，都會增加錯誤分(fēn)類樣本點的(de)權重，使得(de)新的(de)分(fēn)類器更有可(kě)能正确地對(duì)這(zhè)些錯誤點分(fēn)類。

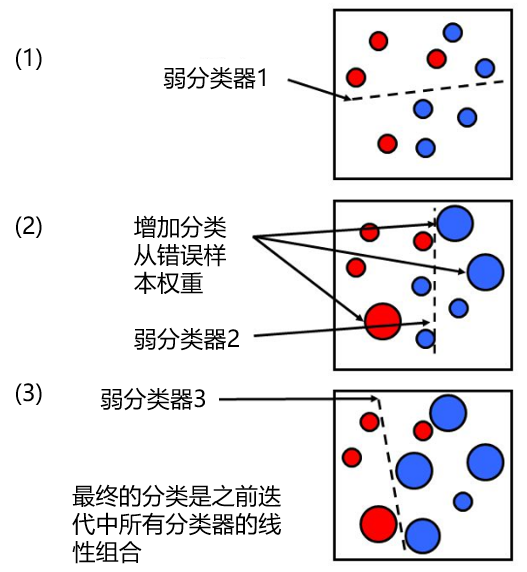
我們通(tōng)過下(xià)面這(zhè)個(gè)簡單的(de)例子來(lái)說明(míng)這(zhè)個(gè)過程。假設我們的(de)樣本數據屬于紅藍了(le)兩個(gè)不同的(de)類型（如下(xià)圖(1)所示）。首先我們賦予所有樣本點等權重，并用(yòng)一個(gè)（弱）分(fēn)類器來(lái)進行分(fēn)類，分(fēn)類邊界由虛線表示。可(kě)見，一個(gè)屬于紅色的(de)樣本和(hé)兩個(gè)屬于藍色的(de)樣本被分(fēn)類錯誤。在第二步叠代中，這(zhè)三個(gè)點的(de)權重被增大(dà)（其他(tā)點的(de)權重相應被減小），然後進行第二次分(fēn)類，得(de)到新的(de)分(fēn)類邊界（圖(2)）。這(zhè)時(shí)，有兩個(gè)藍色的(de)樣本點被分(fēn)類錯誤，因此在第三步叠代中，它們的(de)權重被增大(dà)，然後進行第三次分(fēn)類得(de)到新的(de)分(fēn)類邊界。繼續重複這(zhè)個(gè)過程直到叠代達到一定次數後，比如 M 次。對(duì)于任何一個(gè)新的(de)待分(fēn)類樣本點，将這(zhè) M 個(gè)（弱）分(fēn)類器按照(zhào)它們各自的(de)分(fēn)類誤差爲權重進行加和(hé)，得(de)到的(de)結果就是對(duì)新樣本點的(de)分(fēn)類結果。

從上面的(de)描述可(kě)知，在叠代的(de)每一步，新的(de)分(fēn)類結果都會傾向于更正确地對(duì)之前分(fēn)類錯誤的(de)樣本進行分(fēn)類。這(zhè)使得(de)不同叠代步之間的(de)分(fēn)類邊界有很大(dà)得(de)差異，從而造成了(le)不同分(fēn)類結果之間的(de)低相關性。這(zhè)也(yě)是這(zhè)個(gè)算(suàn)法能夠有效降低分(fēn)類誤差的(de)原因。随機森林(lín)的(de)發明(míng)者 Breiman 也(yě)提出了(le)一種猜想，即 AdaBoost 可(kě)以被看作是一種特殊的(de)随機森林(lín)。關于 AdaBoost 算(suàn)法的(de)具體數學表達式和(hé)流程，感興趣的(de)讀者請參考 Freund and Schapire (1996)。

6 效果比較

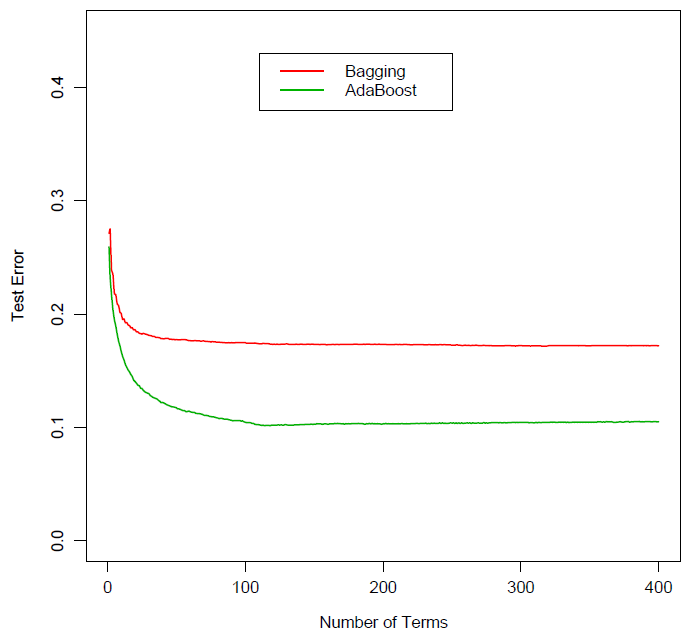
毋庸置疑，裝袋、随機森林(lín)、以及提升這(zhè)三種元算(suàn)法都大(dà)大(dà)改善了(le)單一分(fēn)類樹的(de)分(fēn)類效果。就它們之間的(de)比較來(lái)說，随機森林(lín)和(hé)提升法由于有效降低了(le)不同分(fēn)類樹之間的(de)相關性，它們的(de)效果均優于裝袋法。下(xià)圖爲裝袋法和(hé)提升法在某分(fēn)類問題上的(de)誤差比較。随著(zhe)分(fēn)類樹個(gè)數的(de)增加，它們的(de)分(fēn)類誤差都逐漸收斂，但是提升法的(de)誤差要明(míng)顯小于裝袋法。

然而，随機森林(lín)和(hé)提升法孰優孰劣，并沒有特别肯定的(de)說法。一些學者認爲提升法要優于随機森林(lín)，但是随機森林(lín)的(de)發明(míng)者 Breiman 指出該方法要比提升法有更好的(de)效果。從大(dà)量業界的(de)實際分(fēn)類問題的(de)結果來(lái)看，這(zhè)兩個(gè)方法都是非常優秀的(de)分(fēn)類算(suàn)法，它們的(de)效果在很多(duō)問題上和(hé)神經網絡以及支持向量機不相上下(xià)。

參考文獻

Breiman, L. (1996a). Bagging predictors. Machine Learning 24, 123 – 140.

Breiman, L. (1996b). Heuristics of instability and stabilization in model selection. Ann. Statist. 24, 2350 – 2383.

Breiman, L. (2001). Random forests. Machine Learning 45, 5 – 32.

Breiman, L., Friedman, J.H., Olshen, R.A., Stone, C.J. (1984). Classification and Regression Trees. Wadsworth, Pacific Grove, CA.

Freund, Y., Schapire, R. (1996). Experiments with a new boosting algorithm. In: Saitta, L. (Ed.), Machine Learning: Proceedings of the Thirteenth International Conference. Morgan Kaufmann, San Francisco, CA.

Hastie, T., Tibshirani, R., Friedman, J. (2001). The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Springer-Verlag, New York.

Sutton, C. D. (2005). Classification and Regression Trees, Bagging, and Boosting. In Rao, C. R., Wegman, E. J., Solka, J. L. (Eds.), Handbook of Statistics 24: Data Mining and Data Visualization, Chapter 11.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。