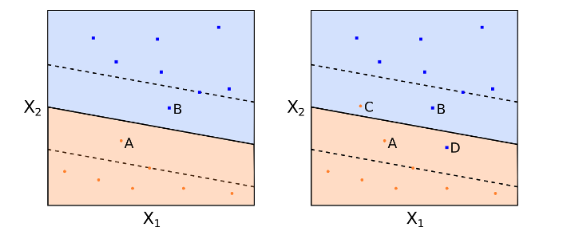
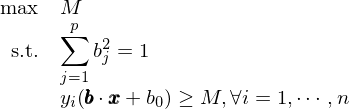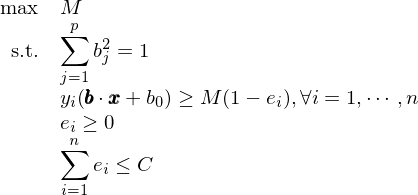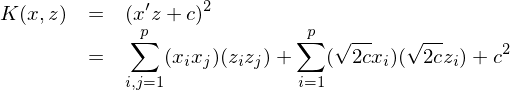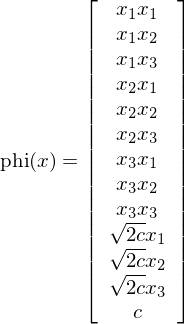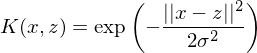一文看懂(dǒng)支持向量機

作者：石川

摘要：這(zhè)篇文章(zhāng)深入淺出的(de)爲你講解監督分(fēn)類算(suàn)法的(de)一大(dà)利器：支持向量機。

1 引言

支持向量機（support vector machines，SVM）是我最早接觸的(de)監督分(fēn)類算(suàn)法之一。早在 MIT 修統計學的(de)時(shí)候，我用(yòng)它做(zuò)過一個(gè)舊(jiù)金山灣區(qū)上班族通(tōng)勤模式的(de)分(fēn)類研究，但當時(shí)隻是很粗淺的(de)認識。後來(lái)由于工作的(de)關系又非常系統的(de)學習(xí)了(le)一下(xià)，這(zhè)其中包括認真學習(xí)了(le)斯坦福 Andrew Ng（吳恩達）的(de)機器學習(xí)課（吳講的(de)真的(de)非常好，深入淺出），參閱了(le)大(dà)量的(de)關于 SVM 的(de)理(lǐ)論和(hé)實際應用(yòng)的(de)文獻，以及和(hé)美(měi)國的(de)一些機器學習(xí)領域專家交換想法，這(zhè)些使我在判斷是否要采用(yòng) SVM 解決量化(huà)投資中的(de)問題時(shí)逐漸變得(de)遊刃有餘。

對(duì)于監督分(fēn)類算(suàn)法的(de)表現，業界常用(yòng)大(dà)概 10 種不同的(de)指标來(lái)評判，包括 Accuracy，LIFT，F-Score，ROC，Precision / Recall Break-Even Point，Root Mean Squared Error 等。無論以哪種準确性的(de)評價指标來(lái)看，SVM 的(de)效果都不輸于人(rén)工神經網絡 ANN 或者高(gāo)級的(de)集合算(suàn)法如随機森林(lín)。SVM 的(de)另一個(gè)特點是其自身可(kě)以在一定程度上防止過拟合，這(zhè)對(duì)于其在量化(huà)投資上的(de)應用(yòng)格外重要。這(zhè)是因爲任何人(rén)工智能算(suàn)法有效的(de)前提是：曆史樣本和(hé)未來(lái)樣本是來(lái)自同一個(gè)（未知）的(de)整體，滿足同分(fēn)布。隻有這(zhè)樣，基于曆史樣本學習(xí)出來(lái)的(de)規律才會在未來(lái)繼續有效。但是對(duì)于金融數據來(lái)說，這(zhè)個(gè)假設在很多(duō)問題上無法滿足。因此，如果機器學習(xí)算(suàn)法在曆史數據上過拟合的(de)話(huà)，那麽基本可(kě)以肯定這(zhè)個(gè)模型對(duì)未來(lái)的(de)數據毫無作用(yòng)。

鑒于我對(duì) SVM 的(de)鐘(zhōng)愛(ài)，我很早以前就打算(suàn)寫一篇介紹它的(de)短文，作爲對(duì)知識的(de)一個(gè)梳理(lǐ)。不過後來(lái)，我讀了(le)一篇來(lái)自 quantstart.com 的(de)文章(zhāng)，名爲 Support Vector Machines: A Guide for Beginners。作者并沒有使用(yòng)大(dà)量的(de)數學公式，而是用(yòng)精煉的(de)語言和(hé)恰如其分(fēn)的(de)圖例對(duì) SVM 的(de)基本原理(lǐ)進行了(le)闡述。平心而論，讓我自己憋幾天也(yě)不一定能寫的(de)比人(rén)家更清晰和(hé)生動，因此今天不如就索性把這(zhè)篇文章(zhāng)大(dà)緻翻譯過來(lái)，作爲對(duì) SVM 的(de)一個(gè)介紹。我會跳過一些不影(yǐng)響理(lǐ)解的(de)文字、對(duì)原文的(de)結構做(zuò)一些改動，并在一些地方加入自己的(de)理(lǐ)解。對(duì)那些閱讀英語比閱讀中文更舒服的(de)小夥伴，也(yě)不妨看看原文。

2 初識 SVM

支持向量機解決的(de)是監督的(de)二元分(fēn)類問題（supervised binary classification）：

垃圾郵件識别就是這(zhè)麽一個(gè)例子：一個(gè)郵件要麽屬于垃圾郵件，要麽屬于非垃圾郵件。對(duì)于一封新郵件，我們希望機器學習(xí)算(suàn)法自動對(duì)它分(fēn)類。爲此，我們首先通(tōng)過人(rén)工對(duì)大(dà)量的(de)曆史郵件進行 spam 或 non-spam 标識，然後用(yòng)這(zhè)些标識後的(de)曆史郵件對(duì)機器學習(xí)算(suàn)法進行訓練。

在處理(lǐ)這(zhè)類分(fēn)類問題時(shí)，SVM 的(de)作用(yòng)對(duì)象是樣本的(de)特征空間（feature space），它是一個(gè)有限維度的(de)向量空間，每個(gè)維度對(duì)應著(zhe)樣本的(de)一個(gè)特征，而這(zhè)些特征組合起來(lái)可(kě)以很好的(de)描述被分(fēn)類的(de)樣本。比如在上面的(de)垃圾郵件識别例子中，一些可(kě)以有效辨别 spam 和(hé) non-spam 郵件的(de)詞彙就構成了(le)特征空間。

爲了(le)對(duì)新的(de)樣本分(fēn)類，SVM 算(suàn)法會根據曆史數據在特征空間内構建一個(gè)超平面（hyperplane）；它将特征空間線性分(fēn)割爲兩個(gè)部分(fēn)，對(duì)應著(zhe)分(fēn)類問題的(de)兩類，分(fēn)别位于超平面的(de)兩側。構建超平面的(de)過程就是模型訓練過程。對(duì)于一個(gè)給定的(de)新樣本，根據它的(de)特征值，它會被放在超平面兩側中的(de)某一側，這(zhè)便完成了(le)分(fēn)類。不難看出，SVM 是一個(gè)非概率的(de)線性分(fēn)類器。這(zhè)是因爲 SVM 模型回答(dá)的(de)是非此即彼的(de)問題，新樣本會被确定的(de)分(fēn)到兩類中的(de)某一類。

在數學上表達上，每一個(gè)曆史樣本點由一個(gè) (x, y) 元組表示，其中粗體的(de) x 是特征向量，即 x = (x_1, …, x_p)，其中每一個(gè) x_j 代表樣本的(de)一個(gè)特征，而 y 代表該樣本的(de)已知分(fēn)類（通(tōng)常用(yòng) +1 和(hé) -1 表示兩個(gè)不同的(de)類）。SVM 會根據這(zhè)些給定的(de)曆史數據來(lái)訓練算(suàn)法的(de)參數，找到最優的(de)線性超平面。理(lǐ)想情況下(xià)，這(zhè)個(gè)超平面可(kě)以将兩類樣本點完美(měi)的(de)分(fēn)開（即沒有錯分(fēn)的(de)情況）。對(duì)于給定的(de)訓練數據，可(kě)以将它們完美(měi)分(fēn)開的(de)超平面很可(kě)能不是唯一的(de)，比如一個(gè)超平面稍微旋轉一個(gè)角度便得(de)到一個(gè)仍然能夠完美(měi)分(fēn)割的(de)超平面。在衆多(duō)的(de)能夠實現分(fēn)類的(de)超平面中，隻有一個(gè)是最優的(de)。我們會在下(xià)文介紹這(zhè)個(gè)“最優”的(de)定義。

在實際應用(yòng)中，很多(duō)數據并非是線性可(kě)分(fēn)的(de)。SVM 的(de)強大(dà)之處在于它不僅僅局限于是一個(gè)高(gāo)維空間的(de)線性分(fēn)類器。它通(tōng)過非線性的(de)核函數（kernel functions）把原始的(de)特征空間映射到更高(gāo)維的(de)特征空間（可(kě)以是無限維的(de)），在高(gāo)維空間中再将這(zhè)些樣本點線性分(fēn)割。高(gāo)維空間的(de)線性分(fēn)割對(duì)應著(zhe)原始特征空間的(de)非線性分(fēn)割，因此在原始特征空間中生成了(le)非線性的(de)決策邊界。此外，這(zhè)麽做(zuò)并不以增加計算(suàn)機的(de)計算(suàn)負擔爲代價。因此 SVM 相當高(gāo)效。

下(xià)面，我們會解釋如何找到最優的(de)線性超平面。基于它引出最大(dà)間隔分(fēn)類器（maximal margin classifier）的(de)概念。通(tōng)過實例，我們會發現最大(dà)間隔分(fēn)類器有時(shí)無法滿足實際問題，這(zhè)是因爲不同類型的(de)樣本點錯綜的(de)交織在一起，讓它們無法被完美(měi)分(fēn)割。爲了(le)解決這(zhè)個(gè)問題，我們必須允許分(fēn)類器故意的(de)錯誤劃分(fēn)一些點，從而得(de)到對(duì)整體樣本總體分(fēn)類效果的(de)最優，這(zhè)便引出了(le)支持向量分(fēn)類器（support vector classifier）。最後，我們介紹核函數的(de)概念。支持向量分(fēn)類器結合核函數便得(de)到了(le)支持向量機。最後，我們總結 SVM 的(de)優缺點。

3 線性超平面

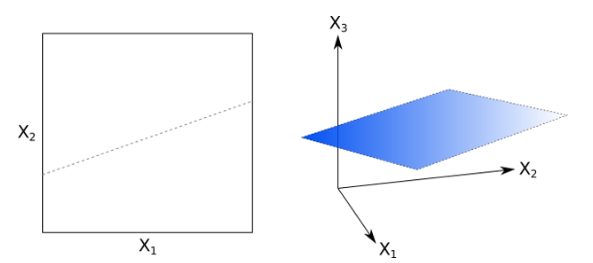
線性超平面是 SVM 的(de)核心。對(duì)于一個(gè) p 維空間，超平面是一個(gè) p-1 維的(de)物(wù)體，它将這(zhè)個(gè) p 維空間一分(fēn)爲二。下(xià)圖分(fēn)别是 2 維和(hé) 3 維特征空間中超平面的(de)例子。在 2 維特征空間中，超平面就是一條 1 維的(de)直線，在 3 維特征空間中，超平面是一個(gè) 2 維的(de)平面。（注意，我們并不要求超平面一定要通(tōng)過特征空間的(de)原點。）

對(duì)于一個(gè) p 維的(de)特征空間 x = (x_1, …, x_p)，我們可(kě)以通(tōng)過下(xià)面這(zhè)個(gè)式子來(lái)定義一個(gè)超平面：

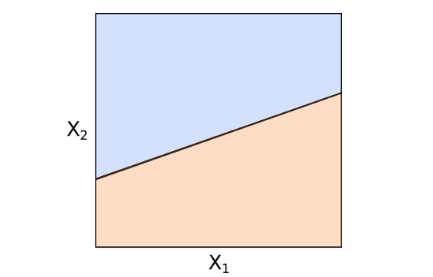
如果用(yòng)向量和(hé)内積來(lái)表達，這(zhè)個(gè)式子變爲 b•x + b_0 = 0。任何滿足這(zhè)個(gè)式子的(de)向量 x 都落在這(zhè)個(gè) p-1 維超平面上。該超平面将 p 維特征空間分(fēn)爲兩個(gè)區(qū)域，如下(xià)圖所示（示意圖，假設 p = 2，兩個(gè)顔色代表特征空間中兩個(gè)不同的(de)區(qū)域）：

如果一個(gè)向量 x 滿足 b•x + b_0 > 0，則它會落在超平面上方的(de)區(qū)域；如果一個(gè)向量 x 滿足 b•x + b_0 < 0，則它會落在超平面下(xià)方的(de)區(qū)域。通(tōng)過判斷 b•x + b_0 的(de)符号，就可(kě)以對(duì) x 分(fēn)類。

4 分(fēn)類問題

在郵件識别的(de)例子中，假設我們有 n 個(gè)曆史郵件，每一封都被标識爲 spam（+1）或者 non-spam（-1）。每一封郵件中都有一些詞被選爲關鍵詞。所有這(zhè) n 封郵件中不重複的(de)關鍵詞就組成了(le)我們的(de)特征。假設不重複的(de)關鍵詞一共有 p 個(gè)。

如果将上面這(zhè)個(gè)問題用(yòng)數學語言轉化(huà)爲分(fēn)類問題，則我們有 n 個(gè)訓練樣本，每一個(gè)樣本都是一個(gè) p 維的(de)特征向量 x_i。此外，每一個(gè)訓練樣本都有一個(gè)已知的(de)分(fēn)類 y_i（例如 spam 或者 non-spam）。因此，我們有 n 對(duì)訓練樣本 (x_i, y_i)。分(fēn)類器将通(tōng)過學習(xí)這(zhè)些訓練樣本來(lái)優化(huà)自身的(de)參數，得(de)到最終的(de)分(fēn)類模型。我們使用(yòng)測試樣本來(lái)檢查分(fēn)類器的(de)分(fēn)類效果。

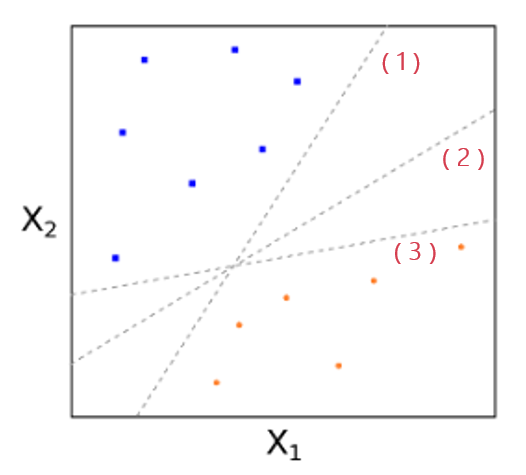
讓我們來(lái)看一個(gè)簡化(huà)的(de)例子。考慮 2 維特征空間并假設訓練樣本都是完美(měi)可(kě)分(fēn)的(de)（如下(xià)圖所示）。圖中，紅色和(hé)藍色代表了(le)兩類不同的(de)樣本點。三天虛線表示三個(gè)不同的(de)超平面；它們都可(kě)以将這(zhè)些點完美(měi)分(fēn)開。

在這(zhè)個(gè)例子中，這(zhè)三條線都可(kě)以将特征空間一分(fēn)爲二。然而，我們如何确定哪條線才是最優的(de)呢(ne)？直觀上說，無論是（1）還(hái)是（3），都離某些紅色和(hé)藍色的(de)樣本點太近了(le)，給我們的(de)感覺是這(zhè)兩條線僅是“将将”把這(zhè)些點分(fēn)開；而位于中間的(de)（2）号虛線離任何紅色的(de)和(hé)藍色的(de)點都比較遠(yuǎn)，給我們的(de)感覺是它非常清晰地将這(zhè)些點區(qū)分(fēn)開了(le)。因此，如果從這(zhè)三條裏面選的(de)話(huà)，（2）号虛線應該是最好的(de)選擇。在數學上，上述直觀感受被精确的(de)翻譯爲數學優化(huà)方程，即最大(dà)間隔超平面。

5 最大(dà)間隔超平面

在上一節中，我們看到能夠實現分(fēn)類的(de)超平面可(kě)能不唯一。在這(zhè)種情況下(xià)我們需要找到最優的(de)。對(duì)于一個(gè)給定的(de)超平面，我們可(kě)以計算(suàn)每個(gè)樣本點到該平面的(de)距離，這(zhè)些距離中最小的(de)一個(gè)就是這(zhè)個(gè)超平面的(de)間隔距離（margin）。因此，對(duì)于每一個(gè)超平面我們可(kě)以計算(suàn)出它的(de) margin。所有可(kě)行的(de)超平面中，margin 最大(dà)的(de)那個(gè)就是我們要找的(de)最優超平面，即最大(dà)間隔超平面（maximal margin hyperplane）。使用(yòng)該超平面進行分(fēn)類的(de)分(fēn)類器就稱爲最大(dà)間隔分(fēn)類器。

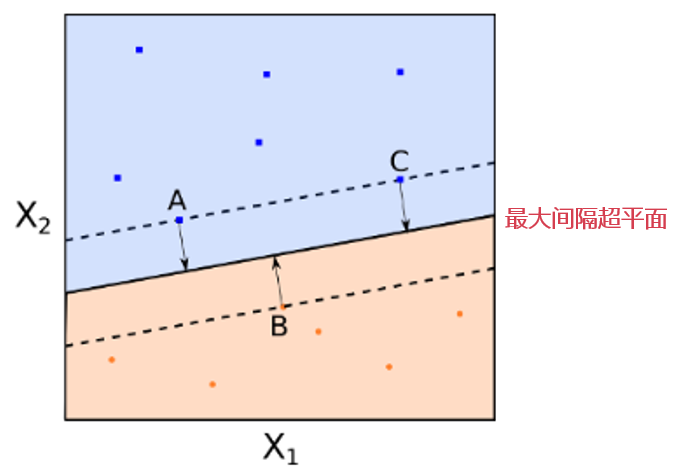
考慮下(xià)面這(zhè)個(gè) 2 維特征空間示意圖。圖中有紅色和(hé)藍色兩類樣本點。黑(hēi)色的(de)實線就是最大(dà)間隔超平面。在這(zhè)個(gè)例子中，A，B，C 三個(gè)點到該超平面的(de)距離相等。注意，這(zhè)些點非常特别，這(zhè)是因爲超平面的(de)參數完全由這(zhè)三個(gè)點确定。該超平面和(hé)任何其他(tā)的(de)點無關。如果改變其他(tā)點的(de)位置，隻要其他(tā)點不落入虛線上或者虛線内，那麽超平面的(de)參數都不會改變。A，B，C 這(zhè)三個(gè)點被稱爲支持向量（support vectors）。最大(dà)間隔超平面非常依賴支持向量的(de)位置（這(zhè)很明(míng)顯是個(gè)缺點，我們會在後面解決）。

在數學上，求解最大(dà)間隔超平面參數相當于求解下(xià)面這(zhè)個(gè)最優化(huà)問題：

這(zhè)個(gè)優化(huà)問題雖然看起來(lái)複雜(zá)，但是它非常容易求解，不過關于它的(de)求解過程不在本文的(de)討(tǎo)論範圍内。需要強調的(de)是，上面的(de)假想例子假設兩類樣本點是可(kě)以完美(měi)的(de)被分(fēn)開的(de)。而在在實際問題中，這(zhè)樣的(de)情況幾乎是不存在的(de)。考慮下(xià)面的(de)例子，紅藍兩類樣本點糾結在一起，我們無法找到一個(gè)超平面将它們完美(měi)的(de)分(fēn)開。

在這(zhè)種情況下(xià)，我們怎麽辦呢(ne)？解決的(de)思路是放松我們的(de)要求，即我們不要求所有的(de)訓練樣本都被正确的(de)分(fēn)類，由此引出軟間隔（soft margin）和(hé)支持向量分(fēn)類器（support vector classifier）的(de)概念。

6 支持向量分(fēn)類器

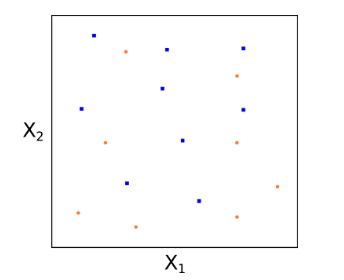
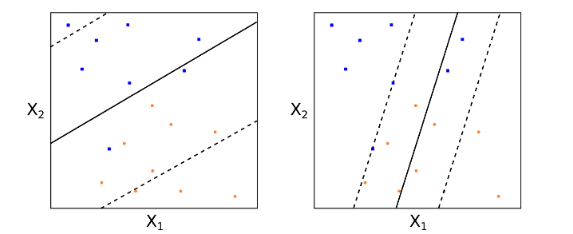
引出軟間隔和(hé)支持向量分(fēn)類器的(de)概念有兩個(gè)動機。第一個(gè)動機是最大(dà)間隔分(fēn)類器非常依賴支持向量的(de)位置，這(zhè)使得(de)它對(duì)新的(de)訓練樣本非常敏感。考慮下(xià)面這(zhè)個(gè)例子，右圖中僅僅因爲增加了(le)一個(gè)訓練樣本而它恰好是支持向量，前後得(de)到的(de)超平面完全不同。很顯然，左圖中的(de)超平面對(duì)所有點的(de)整體分(fēn)類效果更好，而右圖中因爲一個(gè)新樣本的(de)加入，造成了(le)模型的(de)過拟合。

、

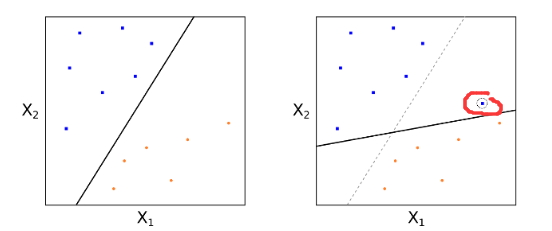
第二個(gè)動機就是上一節最後提到的(de)，實際問題中，訓練樣本幾乎無法被完美(měi)分(fēn)開。爲了(le)解決這(zhè)兩種情況，我們允許一部分(fēn)樣本點被錯誤的(de)分(fēn)類，并以此爲代價追求分(fēn)類器的(de)魯棒性以及分(fēn)類器在全局所有樣本點上分(fēn)類效果的(de)整體最優。一個(gè)支持向量分(fēn)類器允許一些樣本點出現在最大(dà)間隔線之内甚至是超平面錯誤的(de)一側。下(xià)圖左圖中，A、B 兩點雖然沒有被分(fēn)錯類，但它們出現在了(le)最大(dà)間隔邊界（虛線）之内；下(xià)圖右圖中，C 和(hé) D 兩點則出現在超平面錯誤的(de)一側。然而付出這(zhè)些代價所換取的(de)都是中間這(zhè)條整體分(fēn)類效果非常好的(de)超平面（黑(hēi)色實線）。

在數學上，引入 soft margin 後，優化(huà)問題變爲如下(xià)形式：

其中，對(duì)于每一個(gè)訓練樣本點 i，定義了(le)一個(gè)非負的(de)松弛系數 e_i，它的(de)取值表示該點是否滿足最大(dà)間隔。e_i 等于 0 則表示該點滿足最大(dà)間隔；如果 e_i 在 0 和(hé) 1 之間，說明(míng)這(zhè)個(gè)樣本點在最大(dà)間隔邊界之内但仍然分(fēn)類正确；如果 e_i 大(dà)于 1 這(zhè)說明(míng)該點被分(fēn)到了(le)超平面的(de)錯誤一側。系數 C 表示我們允許 soft margin 的(de)程度。C 越小意味著(zhe)我們越不允許出現不滿足最大(dà)間隔的(de)情況。從直觀上說，C 的(de)取值決定了(le)最多(duō)有多(duō)少個(gè)訓練樣本點可(kě)以被分(fēn)類錯誤。下(xià)面的(de)例子說明(míng)，對(duì)于不同的(de) C 的(de)取值，得(de)到的(de)超平面也(yě)會有很大(dà)差異。

一個(gè)分(fēn)類器的(de)誤差由它的(de)偏差和(hé)方差共同決定。在選取 C 時(shí)，我們必須權衡這(zhè)兩者。一個(gè)很小的(de) C 往往意味著(zhe)模型有很低的(de)偏差但是很高(gāo)的(de)方差（因爲新的(de)樣本點會很容易改變超平面的(de)參數）；一個(gè)很大(dà)的(de) C 通(tōng)常意味著(zhe)模型有很高(gāo)的(de)偏差（無法充分(fēn)利用(yòng)數據、找到有效的(de)支持向量）和(hé)較低的(de)方差。在實際應用(yòng)中，C 的(de)取值可(kě)以通(tōng)過交叉驗證來(lái)确定。

7 支持向量機

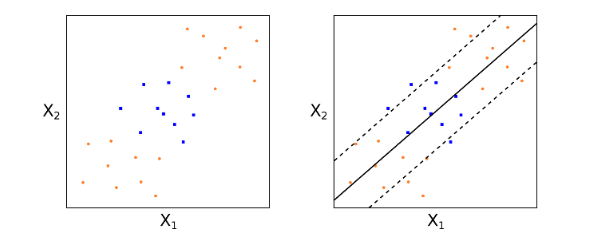
支持向量分(fēn)類器是一個(gè)很好的(de)線性分(fēn)類器（在允許錯誤樣本分(fēn)類的(de)前提下(xià)，找到對(duì)整體最優的(de)超平面）。然而對(duì)于有的(de)問題，數據本身的(de)特性決定了(le)線性分(fēn)類器無論如何也(yě)不可(kě)能取得(de)很好的(de)效果。考慮下(xià)面這(zhè)個(gè)例子。

如果僅使用(yòng)線性的(de)支持向量分(fēn)類器，則隻能得(de)到上圖中黑(hēi)色實線表示的(de)超平面。它的(de)分(fēn)類效果是非常差的(de)。這(zhè)時(shí)，我們就需要對(duì)這(zhè)個(gè)分(fēn)類器進行非線性的(de)變換，這(zhè)就是支持向量機。

這(zhè)裏變換的(de)核心是對(duì)特征空間進行非線性的(de)變換。比如，對(duì)于 p 個(gè)特征 x_1, …, x_p，我們可(kě)以通(tōng)過平方把它們變換到 2p 維的(de)特征空間，即 x_1, (x_1)^2, …, x_p, (x_p)^2。然後在 2p 空間内尋找線性的(de)超平面進行分(fēn)類。雖然超平面在 2p 維度是線性的(de)，但是由于它是原始特征的(de)二次函數，因此從原始特征空間來(lái)看，我們實際上得(de)到了(le)一個(gè)非線性的(de)分(fēn)類器。

那什(shén)麽是核函數呢(ne)？在求解超平面參數的(de)最優化(huà)問題中，最優參數的(de)取值僅僅依賴于訓練樣本特征向量之間的(de)内積。假設兩個(gè)樣本點的(de)特征向量爲 x 和(hé) z，則它們的(de)内積爲 x•z（或者 (x^T)z）。假設特征空間的(de)非線性映射爲 phi，因此在映射後我們的(de)樣本特征向量變爲 phi(x) 和(hé) phi(z)。在這(zhè)個(gè)新的(de)特征空間求解超平面時(shí)，我們需要使用(yòng)的(de)實際上是 phi(x)•phi(z)。對(duì)于這(zhè)個(gè)映射，我們定義它對(duì)應的(de)核函數爲：K(x, z) = phi(x)•phi(z)。

因此，在優化(huà)問題的(de)求解中，我們隻要把 x•z 都替換爲 K(x, z) 就相當于是在 phi 這(zhè)個(gè)映射下(xià)的(de)特征空間内求解超平面。當我們知道映射 phi 的(de)形式後，可(kě)以通(tōng)過分(fēn)别計算(suàn) phi(x) 和(hé) phi(z)，然後再求它們的(de)内積得(de)到 K(x, z)。然而，這(zhè)對(duì)于計算(suàn)機來(lái)說是非常低效的(de)。假如原始特征空間的(de)維度爲 p，而我們把它映射到維度爲 p^2 的(de)特征空間，則 SVM 算(suàn)法的(de)計算(suàn)量就由 O(p) 變成了(le) O(p^2)。如果 p 很大(dà)的(de)話(huà)（在很多(duō)實際問題中，p 是非常大(dà)的(de)），這(zhè)麽做(zuò)會大(dà)大(dà)的(de)損害 SVM 的(de)效率。

對(duì)此，核函數的(de)優勢是，對(duì)于很多(duō)應用(yòng)中常見的(de)特征空間映射 phi 函數，核函數 K(x, z) 存在一個(gè)非常方便計算(suàn)的(de)解析式。通(tōng)過計算(suàn)這(zhè)個(gè)解析式，我們便可(kě)以繞過計算(suàn) phi(x) 和(hé) phi(z)，而直接得(de)到 K(x, z) 的(de)取值。然後我們隻需要将 K(x, z) 的(de)值帶到最優化(huà)參數的(de)解中，便可(kě)得(de)到最優的(de)超平面。這(zhè)大(dà)大(dà)的(de)降低了(le) SVM 的(de)計算(suàn)時(shí)間，使其成爲高(gāo)維空間分(fēn)類的(de)利器。

讓我們來(lái)看一個(gè)例子，考慮下(xià)面這(zhè)個(gè)核函數（它又稱作多(duō)項式核）：

它的(de)計算(suàn)量隻有 O(p)。當 p = 3 時(shí)，它對(duì)應的(de)映射 phi 卻是下(xià)面這(zhè)個(gè) 13 維空間：

僅僅通(tōng)過計算(suàn)核函數的(de)表達式就相當于巧妙的(de)進行了(le)從 3 維到 13 維空間的(de)非線性映射，這(zhè)是多(duō)麽美(měi)妙！SVM的(de)核心就是通(tōng)過使用(yòng)核函數（某一個(gè)給定的(de)非線性方程），将原始的(de)特征空間變換爲更高(gāo)維的(de)特征空間。常見的(de)核函數除了(le)上面這(zhè)個(gè)多(duō)項式核外，還(hái)有徑向基（高(gāo)斯）核。它的(de)表達式如下(xià)，這(zhè)裏不再贅述。

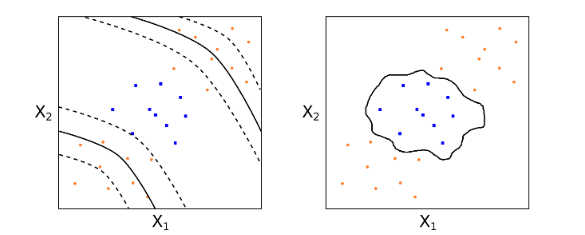
對(duì)于前面那個(gè)線性分(fēn)類器無能爲力的(de)例子，在使用(yòng)了(le)适當的(de)核函數後，我們可(kě)以在原始特征空間得(de)到非線性的(de)分(fēn)類邊界（下(xià)面左圖使用(yòng)了(le)多(duō)項式核，右圖使用(yòng)了(le)高(gāo)斯核）。顯然，它們的(de)分(fēn)類效果比線性分(fēn)類器的(de)效果要好很多(duō)，這(zhè)是因爲它們充分(fēn)利用(yòng)了(le)訓練數據的(de)非線性特征。

8 SVM 的(de)優缺點

優點：

缺點：

9 結語

SVM 算(suàn)是監督分(fēn)類算(suàn)法的(de)一個(gè)利器。它原理(lǐ)清晰、計算(suàn)高(gāo)效、易在高(gāo)維空間處理(lǐ)非線性關系。但是，和(hé)任何一個(gè)機器學習(xí)算(suàn)法一樣，最難的(de)不是使用(yòng)一個(gè)算(suàn)法，而是真正明(míng)白我們要解決的(de)問題。如果問題的(de)本質需要非線性分(fēn)類邊界，而我們使用(yòng)了(le)線性的(de)核函數，那結果可(kě)想而知。反過來(lái)也(yě)是一樣。在今後的(de)討(tǎo)論中，我們還(hái)會進一步從實戰的(de)角度介紹如何有效的(de)使用(yòng) SVM。

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。