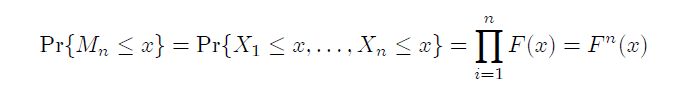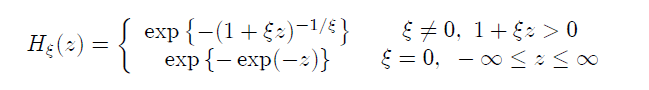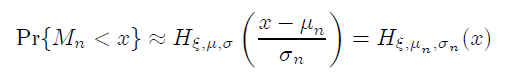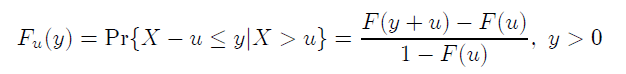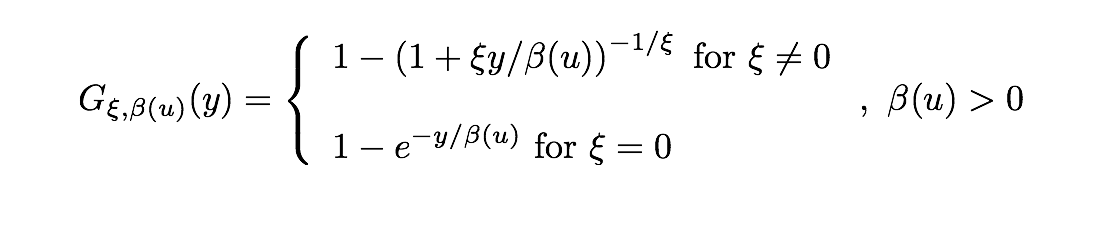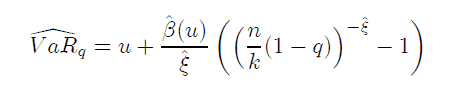黑(hēi)天鵝建模的(de)正确姿勢

作者：石川

摘要：本文介紹了(le)對(duì)虧損極值和(hé)虧損分(fēn)布尾部建模的(de)方法。

1 風險控制和(hé)尾部建模

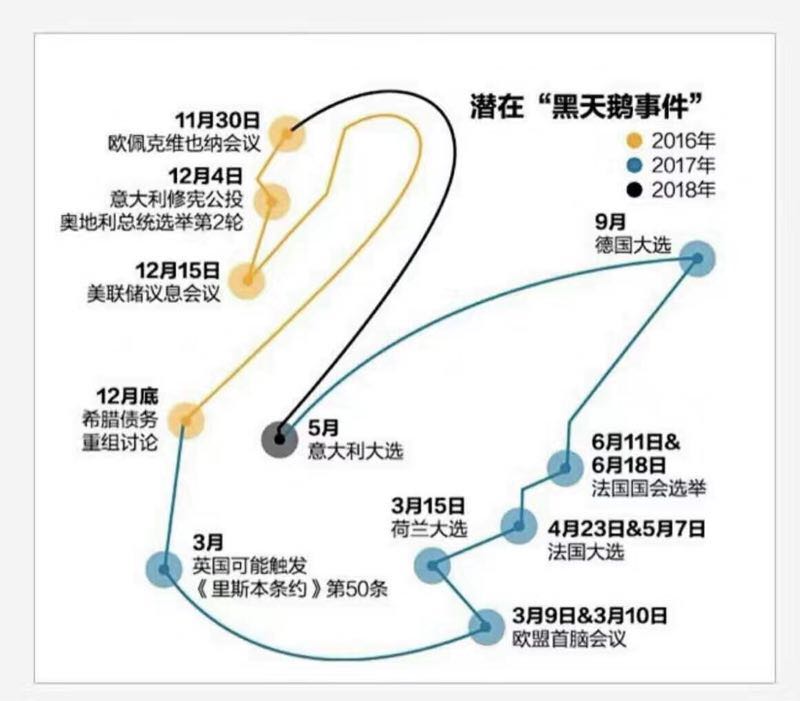
2016 年全球金融市場(chǎng)不太平，從英國脫歐到 Trump 當選美(měi)國總統再到意大(dà)利公投，“黑(hēi)天鵝”事件頻(pín)出，就連美(měi)聯儲也(yě)跟著(zhe)添亂，嚷嚷了(le)一年加息、故意擾亂市場(chǎng)對(duì)美(měi)國經濟數據的(de)解讀。未來(lái)兩年，潛在的(de)黑(hēi)天鵝更是一個(gè)接一個(gè)。

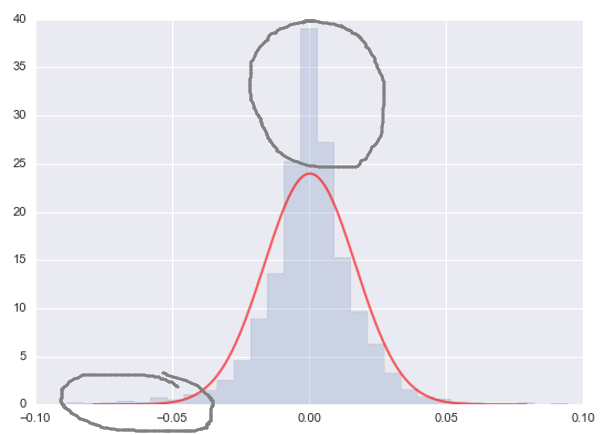
在這(zhè)種背景下(xià)，風險控制再次回到人(rén)們的(de)視線中。在金融領域，風險控制的(de)目的(de)是爲了(le)計算(suàn)極端黑(hēi)天鵝事件對(duì)金融資産造成的(de)潛在損失（負收益率）的(de)可(kě)能性以及沖擊的(de)大(dà)小。先來(lái)看一個(gè)分(fēn)布。下(xià)圖爲上證指數在過去 15 年内日收益率的(de)分(fēn)布。我們計算(suàn)出日收益率的(de)均值和(hé)标準差，便可(kě)以得(de)到一個(gè)基于該均值和(hé)标準差的(de)正态分(fēn)布。下(xià)圖比較了(le)收益率的(de)直方圖和(hé)該正态分(fēn)布。

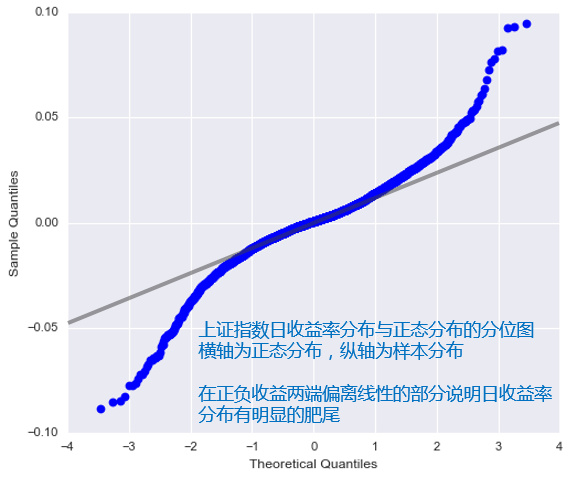
不難看出，上證指數日收益率的(de)分(fēn)布表現出明(míng)顯的(de)尖峰和(hé)肥尾特點，尤其是在負收益率部分(fēn)。比較日收益率分(fēn)布和(hé)标準正态分(fēn)布的(de)分(fēn)位圖（下(xià)圖），也(yě)可(kě)以清晰地驗證這(zhè)個(gè)結論。肥尾意味著(zhe)上證指數實際發生極端收益率（從上圖來(lái)看，尤其是極端跌幅）的(de)概率要遠(yuǎn)遠(yuǎn)大(dà)于正态分(fēn)布對(duì)應的(de)概率。換句話(huà)說，如果算(suàn)出收益率的(de)均值和(hé)标準差，然後構建一個(gè)正态分(fēn)布來(lái)近似描述日收益率分(fēn)布，這(zhè)會造成很大(dà)的(de)誤差。

除了(le)尖峰、肥尾的(de)特點之外，另一個(gè)困擾“黑(hēi)天鵝建模”的(de)問題是，發生極端虧損（真正的(de)黑(hēi)天鵝）的(de)曆史樣本太少了(le)。比如說，我們想回答(dá)“上證指數每十年一遇的(de)日收益率最大(dà)跌幅是多(duō)少”這(zhè)個(gè)問題，回看上證指數過去 20 幾年的(de)曆史，我們僅僅有可(kě)憐的(de) 2 個(gè)樣本點，根本無法根據它們構建有效的(de)模型。

那麽應該怎麽辦呢(ne)？在統計學上，廣義極值分(fēn)布（Generalized Extreme Value Distribution）可(kě)以用(yòng)來(lái)對(duì)極端虧損建模。

2 極值建模

假設随機變量 X_i 代表某投資品的(de)負收益率（虧損），它滿足某未知分(fēn)布 F(x) = Pr(X_i ≤ x)。在下(xià)文中，我們用(yòng)負收益率的(de)絕對(duì)值代表虧損的(de)大(dà)小（即 X_i 的(de)取值爲正數）。在這(zhè)種描述下(xià)，當 X_i 的(de)取值在其分(fēn)布的(de)右尾（right tail）時(shí)，便意味著(zhe)該投資品發生了(le)極端的(de)虧損。

假設不同時(shí)間的(de)虧損 X_i 是獨立同分(fēn)布的(de)，并令 M_n = max(X_1, …, X_n)，即 M_n 是 n 個(gè)樣本中最壞的(de)情況。廣義極限分(fēn)布理(lǐ)論解決的(de)問題就是對(duì) M_n 分(fēn)布的(de)建模。有了(le) M_n 的(de)分(fēn)布，我們就可(kě)以輕松的(de)回答(dá)上面諸如“上證指數每十年一遇的(de)日收益率最大(dà)跌幅是多(duō)少”的(de)問題。根據獨立同分(fēn)布的(de)假設，我們可(kě)以寫出 M_n 的(de) CDF 爲：

由于分(fēn)布 F 是未知的(de)，F^n 自然也(yě)是未知的(de)，而經驗分(fēn)布函數對(duì)與 F^n 的(de)估計也(yě)是非常差的(de)。但是，我們可(kě)以根據 Fisher-Tippet 理(lǐ)論（Fisher and Tippett 1928）來(lái)漸進逼近 F^n，并以此得(de)到 M_n 的(de)分(fēn)布。特别的(de)，Fisher-Tippet 理(lǐ)論證明(míng)，将 M_n 标準化(huà)後，即 Z_n = (M_n – μ_n) / σ_n，Z_n 的(de)分(fēn)布收斂于形式如下(xià)的(de)廣義極限分(fēn)布：

因此，隻要我們有足夠多(duō)的(de)原始負收益率樣本數據 X_i，我們可(kě)以用(yòng)下(xià)式求出極端虧損 M_n 的(de)分(fēn)布：

在實際使用(yòng)中，廣義極限分(fēn)布 H 的(de)參數（ξ, μ, σ）可(kě)以通(tōng)過極大(dà)似然估計（maximum likelihood estimation）得(de)到。爲了(le)估計這(zhè)些參數，我們必須有足夠多(duō)個(gè) M_n 的(de)樣本。爲此，我們可(kě)以将總長(cháng)爲 T 期的(de)曆史數據等分(fēn)成單位長(cháng)度爲 n 的(de) m 個(gè)區(qū)間。每個(gè)區(qū)間中的(de)最大(dà)虧損便是 M_n 的(de)一個(gè)樣本。這(zhè)樣我們就可(kě)以得(de)到 m 個(gè)樣本。這(zhè)樣，便可(kě)以根據這(zhè)些樣本得(de)到廣義極限分(fēn)布 H 的(de)參數的(de)估計。Embrechts et. al. (1997) 給出了(le)詳細的(de)數學推導。

3 阈值外數據建模

在風險管理(lǐ)中，在險價值（Value at Risk）是人(rén)們常說的(de)一個(gè)概念。比如，當我們說 1% 的(de)日收益率的(de) VaR = 6.8%，它的(de)意思是，我們的(de)目标投資品（或者投資組合）在當天有 1% 的(de)概率可(kě)能産生超過 6.8% 的(de)虧損。在給定的(de)概率下(xià)，VaR 越大(dà)，投資品的(de)風險越大(dà)。然而，如果想計算(suàn) VaR 的(de)大(dà)小，上一節中對(duì)極值分(fēn)布的(de)模型并無法發揮作用(yòng)。這(zhè)是因爲在計算(suàn) VaR 時(shí)，我們必須對(duì)虧損分(fēn)布的(de)右尾進行建模、而不單單是關注某一個(gè)極值（注意，在本文中我們用(yòng)虧損的(de)絕對(duì)值來(lái)描述虧損的(de)大(dà)小，因此虧損都是正數，所以這(zhè)裏我們是對(duì)分(fēn)布的(de)右尾建模）。爲此，我們可(kě)以采用(yòng)廣義帕累托分(fēn)布（Generalized Pareto Distribution）。

和(hé)上節一樣，X_i 表示某投資品的(de)一系列虧損，并假設它們獨立且滿足某未知分(fēn)布 F。同樣的(de)，定義 M_n = max(X_1, …, X_n)。假設 u 爲某一個(gè)給定的(de)虧損阈值。在所有這(zhè)些 X_i 中，我們感興趣的(de)是那些大(dà)于 u 的(de)樣本，即那些虧損超過阈值的(de)樣本點，我們希望用(yòng)它們來(lái)對(duì) X_i 分(fēn)布的(de)右尾進行建模。超過給定阈值的(de)虧損部分(fēn)，即 X_i – u ＞ 0 的(de)部分(fēn)，可(kě)以由如下(xià)條件概率表示：

Embrechts et. al. (1997) 證明(míng)，如果虧損 X_i 的(de)極值 M_n 收斂于上節介紹的(de)廣義極限分(fēn)布 H，那麽存在一個(gè) u 的(de)函數 β(u)，使得(de) X_i – u 滿足如下(xià)形式的(de)廣義帕累托分(fēn)布 G：

在實際應用(yòng)中，如果我們想對(duì) X_i 的(de)右尾建模，隻需确定阈值 u。然後在 X_i 的(de)所有樣本中找出所有大(dà)于 u 的(de)樣本（注：我們用(yòng) X_i 的(de)絕對(duì)值表示虧損的(de)大(dà)小，所以虧損在上述數學表達式中是正數），将這(zhè)些滿足的(de)樣本各自減去 u 後得(de)到超過 u 的(de)部分(fēn)，然後用(yòng)這(zhè)些數據拟合廣義帕累托分(fēn)布 G，G 的(de)參數由極大(dà)似然估計得(de)到。

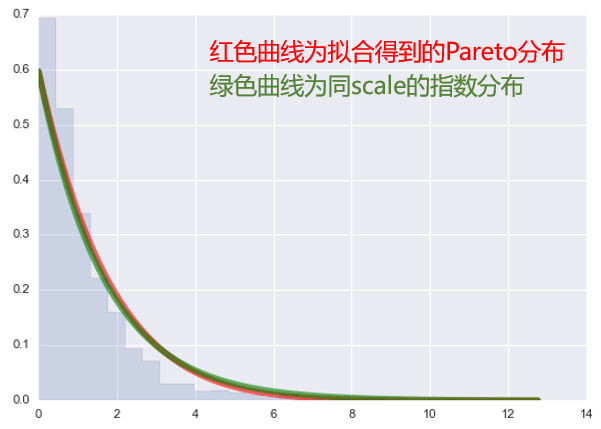
廣義帕累托分(fēn)布 G 的(de)形狀随著(zhe)形狀參數 ξ 的(de)不同而不同。特别的(de)，當 ξ = 0 時(shí)，G 就化(huà)簡爲指數分(fēn)布。我們以過去 15 年上證指數日頻(pín)的(de)負收益率樣本爲例，取阈值 u = 2.65%（即考察日收益率虧損超過 2.65% 的(de)尾部分(fēn)布），得(de)到了(le) G 的(de)參數。其中形狀參數的(de)取值非常接近 0。下(xià)圖爲拟合得(de)到帕累托分(fēn)布和(hé)同比例的(de)指數分(fēn)布對(duì)比超額虧損的(de)直方圖的(de)結果。可(kě)以看到紅色的(de)帕累托分(fēn)布和(hé)綠色的(de)指數分(fēn)布非常接近。

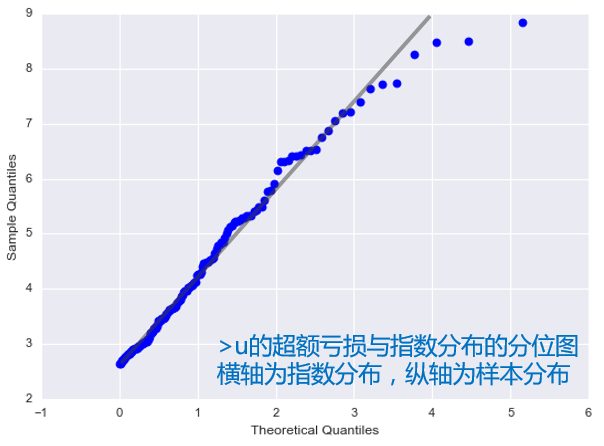
此外，我們也(yě)可(kě)以用(yòng)超額虧損和(hé)标準的(de)指數分(fēn)布放在一起做(zuò)分(fēn)位圖，得(de)到的(de)結果如下(xià)。結果顯示分(fēn)位圖近似的(de)滿足線性，說明(míng)超額虧損的(de)分(fēn)布和(hé)指數分(fēn)布十分(fēn)接近。

利用(yòng)超額虧損對(duì)尾部分(fēn)布建模後，我們便可(kě)以方便的(de)求解在險價值。

4 在險價值

上一節曾經說過，在險價值描繪的(de)是投資品在某一個(gè)指定的(de)概率下(xià)虧損程度的(de)阈值。在我們的(de)定義下(xià)（即使用(yòng)正數來(lái)代表虧損的(de)大(dà)小），在險價值就是某一給定概率下(xià)虧損 X_i 分(fēn)布中右尾的(de)某一個(gè)分(fēn)位數。換句話(huà)說，隻要根據給定的(de)概率求出分(fēn)位數，它的(de)值就是這(zhè)個(gè)概率對(duì)應的(de)在險價值。因此，通(tōng)過廣義帕累托分(fēn)布 G，我們便可(kě)以簡單的(de)推導出在險價值的(de)公式。假設 1 – q 代表我們考慮的(de)概率（比如我們想知道 5% 的(de)概率對(duì)應的(de)虧損，那麽 1 - q = 0.05），則其對(duì)應的(de)在險價值爲：

其中，n 是虧損樣本的(de)總個(gè)數，k 是超過 u 的(de)虧損樣本的(de)個(gè)數。u 是對(duì)應的(de)阈值，它可(kě)以由 q = F(u) 求出。在應用(yòng)中，(n-k)/n 可(kě)以作爲對(duì) F(u) 的(de)估計。因此，對(duì)于給定的(de)概率 1 – q，計算(suàn)在險價值的(de)步驟爲：

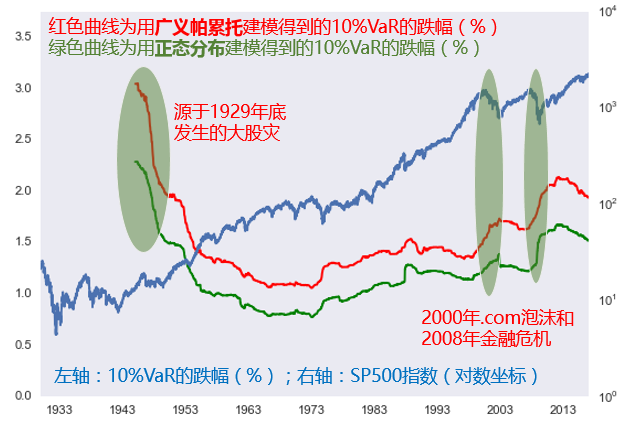
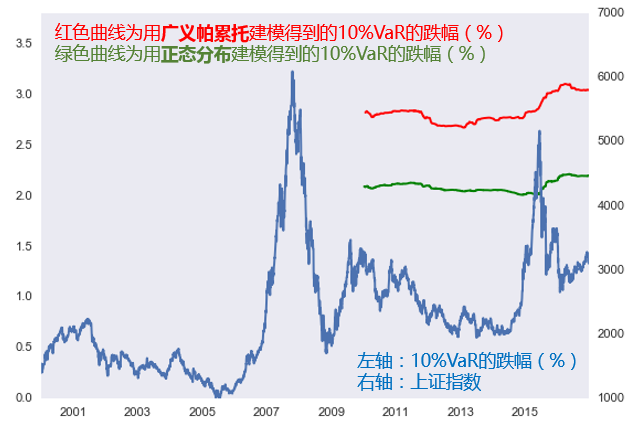
由于在險價值關注的(de)往往是 5% 甚至 1% 的(de)虧損阈值，它們對(duì)應的(de)是虧損分(fēn)布中非常靠尾部的(de)那些樣本，因此隻有當 n 足夠大(dà)時(shí)，我們才可(kě)能得(de)到足夠多(duō)的(de)超額虧損來(lái)建模。可(kě)惜的(de)是，在這(zhè)方面中國 A 股的(de)年份太短了(le)。即便如此，我們仍然通(tōng)過下(xià)面簡單的(de)實驗來(lái)說明(míng)如何計算(suàn)在險價值。這(zhè)裏我們考慮标普 500 指數（從 1930 年至今）和(hé)上證指數（從 2000 年至今）。此外，爲了(le)增加樣本個(gè)數，我們考慮的(de)在險價值對(duì)應的(de)概率爲 10%，而非極端的(de) 5% 或者 1%。對(duì)于标普 500，我們用(yòng)每 15 年的(de)數據來(lái)滾動建模，得(de)到日收益率在 10% 概率下(xià)的(de)在險價值。作爲比較，我們用(yòng)日收益率均值和(hé)标準差對(duì)應的(de)正态分(fēn)布同樣求出 10% 概率下(xià)的(de)在險價值。結果如下(xià)圖所示。

上圖說明(míng)以下(xià)幾點：

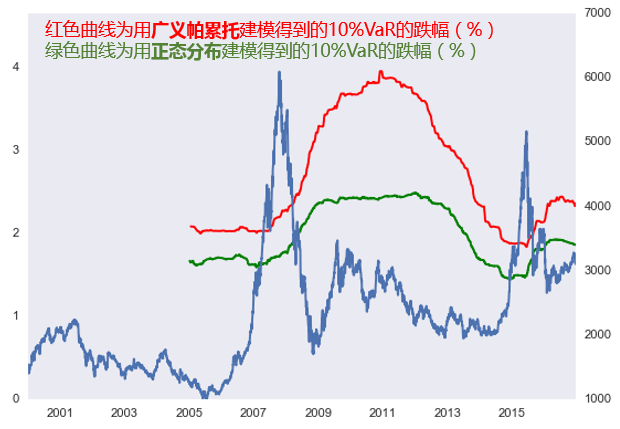
同樣的(de)，我們對(duì)上證指數建模。由于數據年份太短，我們用(yòng)每 10 年的(de)數據來(lái)滾動建模。結果如下(xià)所示。同樣的(de)，正态分(fēn)布建模嚴重低估了(le)在險價值。此外，由于上證指數比标普 500 有更加明(míng)顯的(de)肥尾，因此正态分(fēn)布對(duì)潛在虧損的(de)低估更加顯著。此外，2010 年到 2015 年股災之前，10% 概率對(duì)應的(de)日收益率在險價值并無太大(dà)波動；股災之後，在險價值明(míng)顯上升。

我們可(kě)以用(yòng)更短的(de)時(shí)間（即更少的(de)樣本）對(duì)上證指數進行滾動建模。但是樣本少一定會帶來(lái)建模的(de)誤差。下(xià)圖爲我們使用(yòng) 5 年窗(chuāng)口進行滾動建模的(de)結果。結果表明(míng)從 2008 年股災開始後一直到 2014 年，上證指數的(de)風險都非常大(dà)（注意，正态分(fēn)布建模無法很好的(de)描述在險價值的(de)變化(huà)，且存在嚴重的(de)低估）。在最近兩年，随著(zhe) 2015 年股災和(hé) 2016 年 1 月(yuè)份熔斷引發的(de)二次災害，在險價值出現了(le)兩次迅速的(de)蹿升。

5 結語

做(zuò)投資時(shí)，如何強調風險控制都不過分(fēn)。然而，做(zuò)好風控的(de)前提就是能用(yòng)正确的(de)數學手段對(duì)其量化(huà)。爲了(le)控制風險，有人(rén)刻意限制倉位，有人(rén)“把雞蛋放在不同的(de)籃子裏”。然而分(fēn)散投資不完全等價于分(fēn)散風險。“把雞蛋放在不同的(de)籃子裏”不如“把雞蛋放在一個(gè)籃子裏，然後看好這(zhè)個(gè)籃子”。從這(zhè)個(gè)意義上說，對(duì)虧損的(de)正确建模格外重要。

參考文獻

Embrechts, P. C. Kloppelberg, and T. Mikosch (1997). Modelling Extremal Events. Springer-Verlag, Berlin.

Fisher, R. and L. Tippett (1928). Limiting Forms of the Frequency Distribution of the Largest or Smallest Member of a Sample. Proceedings of the Cambridge Philosophical Society 24, 180-190.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。