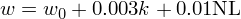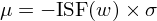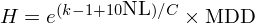模型複雜(zá)度随想

作者：石川

摘要：當模型複雜(zá)度一樣時(shí)，人(rén)們偏好風險收益特性更高(gāo)的(de)策略；當風險收益特性一樣時(shí)，人(rén)們偏好模型複雜(zá)度更低的(de)策略。各種複雜(zá)模型帶來(lái)的(de)邊際超額收益能否 justify 它們的(de)複雜(zá)度呢(ne)？拭目以待。

1 引言

一個(gè)初入量化(huà)投資的(de)分(fēn)析師經過了(le)一個(gè)月(yuè)的(de)奮鬥開發出了(le)一個(gè)雙均線趨勢追蹤模型後，興沖沖的(de)跑來(lái)和(hé)他(tā)的(de)基金經理(lǐ)彙報，于是便有了(le)下(xià)面這(zhè)段對(duì)話(huà)。

上面這(zhè)段對(duì)話(huà)當然是我杜撰的(de)。想通(tōng)過它表明(míng)的(de)觀點是，我們将不同的(de)量化(huà)技術應用(yòng)到同樣的(de)數據上構建某一類（比如趨勢追蹤、反轉、套利）策略時(shí)，最終會挑出來(lái)表現最好的(de)量化(huà)技術，無論這(zhè)個(gè)技術複雜(zá)與否（線性的(de)、非線性的(de)），這(zhè)個(gè)過程本身就是在過拟合。最終被挑出來(lái)的(de)，注定是因爲在樣本内戰勝了(le)其他(tā)的(de)。從“超參數”（見《科學回測中的(de)大(dà)學問》）的(de)意義上說，這(zhè)個(gè)模型難逃 data mining 之嫌，因爲它比别的(de)模型更好很可(kě)能是因爲它對(duì)樣本數據内的(de)噪聲刻畫(huà)的(de)更精準，而非發現了(le)一些被其他(tā)策略忽視到的(de)真實存在于數據之間的(de)因果關系。

以上這(zhè)點粗淺的(de)認識當然不是鼓勵大(dà)家放棄回測中表現好的(de)、使用(yòng)表現差的(de)量化(huà)技術。就我自己有限的(de)經驗來(lái)看，任何策略都或多(duō)或少存在數據挖掘的(de)問題，而這(zhè)個(gè)問題随著(zhe)模型複雜(zá)度的(de)增加更加突出。今天就簡單聊聊模型複雜(zá)度。討(tǎo)論主要從以下(xià)兩個(gè)角度展開：

這(zhè)兩個(gè)角度的(de)研究都是很大(dà)的(de)課題，本文僅僅是做(zuò)一點抛磚引玉的(de)探討(tǎo)。

2 模型複雜(zá)度和(hé)過拟合程度

在構建一個(gè)量化(huà)投資策略時(shí)，一旦确定了(le)模型複雜(zá)度，就要進行參數優化(huà)。隻要是參數優化(huà)，無論再怎麽小心，都會存在過拟合。本節使用(yòng)趨勢策略闡述在給定的(de)模型複雜(zá)度進行參數優化(huà)和(hé)過拟合程度之間的(de)關系。分(fēn)析流程如下(xià)：

分(fēn)析中采用(yòng)的(de)趨勢追蹤策略是均線多(duō)頭排列策略。它的(de)定義和(hé)模型複雜(zá)度介紹如下(xià)。在市場(chǎng)有大(dà)趨勢的(de)時(shí)候，均線一般呈現多(duō)頭或者空頭結構，即不同周期 T 的(de)均線排序和(hé) T 的(de)排序非常一緻（比如上漲時(shí)，通(tōng)常有 MA5 > MA15 > MA30）。當投資品從上漲向下(xià)跌轉換、或由下(xià)跌向上漲轉換時(shí)，短周期均線會先于長(cháng)周期均線發生變化(huà)。在前者發生時(shí)，短周期均線開始逐步下(xià)穿長(cháng)周期均線；在後者發生時(shí)，短周期均線開始逐步上穿長(cháng)周期均線。在發生由漲轉跌或由跌轉漲時(shí)，不同周期均線的(de)排序和(hé)時(shí)間窗(chuāng)口 T 大(dà)小的(de)排序關系被打亂，不再完全一緻。

使用(yòng)秩相關系數計算(suàn)均線排序和(hé)時(shí)間窗(chuāng)口 T 排序之間的(de)一緻性，并使用(yòng)它擇時(shí)、構建趨勢追蹤策略（這(zhè)裏隻考慮多(duō)頭策略）。當均線多(duō)頭排列時(shí)，均線和(hé) T 之間的(de)秩相關性爲 1；當均線空頭排列時(shí)，均線和(hé) T 之間的(de)秩相關性爲 -1。由漲轉跌時(shí)，短期均線開始下(xià)穿，秩相關性從 1 開始下(xià)降；由跌轉漲時(shí)，短期均線開始上穿，秩相關性從 -1 開始上升。由此，可(kě)以構建策略如下(xià)：

在這(zhè)個(gè)策略中，模型複雜(zá)度由如下(xià)兩組參數刻畫(huà)：

這(zhè)兩組參數各自從不同層面增加了(le)模型的(de)複雜(zá)程度。在分(fēn)析中，它們的(de)取值如下(xià)：

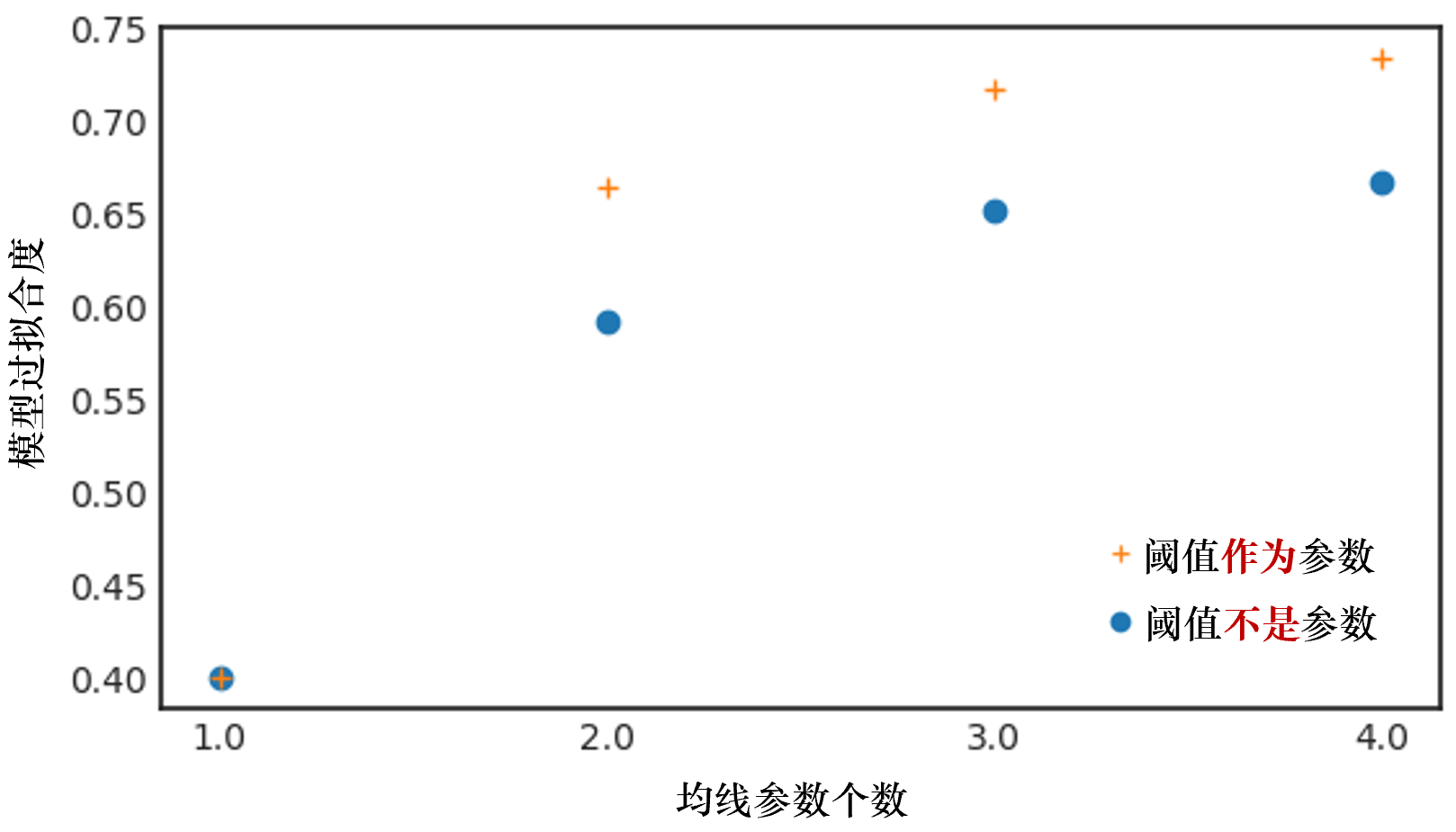
依照(zhào)上述描述進行實驗，得(de)到的(de)模型複雜(zá)度和(hé)過拟合程度的(de)關系如下(xià)圖所示。其中藍色圓圈表示僅考慮均線參數個(gè)數這(zhè)一種模型複雜(zá)度時(shí)的(de)情況，而黃(huáng)色十字表示同時(shí)考慮阈值作爲模型複雜(zá)度的(de)情況。

當我們使用(yòng)真實的(de)交易數據進行策略的(de)參數優化(huà)時(shí)，盡管使用(yòng)了(le)訓練集和(hé)測試集、考慮了(le)參數平原、從各種業務層面解釋了(le)參數的(de)選擇，依然無法消除參數優化(huà)中過拟合的(de)影(yǐng)響。更不幸的(de)是，對(duì)于真實交易數據，由于不知道它其中哪些是因果關系、哪些是噪聲，因此我們甚至無法評價參數優化(huà)造成的(de)過拟合程度。然而在上述實驗中，由于價格序列由随機遊走生成，因此随著(zhe)實驗個(gè)數的(de)增加，我們預期它們的(de)基礎夏普率均值是 0。這(zhè)正是使用(yòng) random walks 來(lái)驗證策略的(de)好處，因爲它的(de)“正确答(dá)案”是已知的(de) —— 一個(gè)不存在過拟合的(de)策略在随機遊走價格序列上不應該能持續的(de)賺到錢。

這(zhè) 100 個(gè) random walks 的(de)基礎夏普率均值爲 -0.03。如果參數優化(huà)中沒有過拟合，那麽策略夏普率均值和(hé)基礎夏普率均值相差不遠(yuǎn)。然而，分(fēn)析的(de)結果遠(yuǎn)非如此。上圖表明(míng)，随著(zhe)參數的(de)增多(duō)，模型的(de)過拟合程度（100 個(gè)策略夏普率均值于基礎家譜率均值之差）也(yě)在上升；而随著(zhe)模型複雜(zá)度從多(duō)維度的(de)提升（即加入阈值參數），模型的(de)過拟合程度産生了(le)跳變。上述結果說明(míng)模型的(de)過拟合程度随模型的(de)複雜(zá)度遞增。

3 模型複雜(zá)度和(hé)損失痛苦

本節來(lái)看看模型複雜(zá)度和(hé)策略損失帶來(lái)的(de)主觀感受之間的(de)關系。《追求卓越，但接受交易中的(de)不完美(měi)》一文曾闡述了(le)如下(xià)觀點：一個(gè)策略投放到實盤時(shí)最大(dà)的(de)敵人(rén)是交易者的(de)心理(lǐ)關。這(zhè)個(gè)心理(lǐ)關指的(de)是交易者能否克服實盤中的(de)心理(lǐ)壓力從而堅持使用(yòng)這(zhè)個(gè)策略。對(duì)于任何一個(gè)量化(huà)投資策略，幾乎可(kě)以确定的(de)是它在回測中的(de)表現是其在實盤中表現的(de)上限。在實際交易中，價格時(shí)刻在波動，充斥著(zhe)噪聲的(de)各路消息以遠(yuǎn)超過我們能夠接受的(de)速度湧來(lái)，使人(rén)快(kuài)步踏入行爲金融學中的(de)各種認知偏差陷阱、喪失冷(lěng)靜；面對(duì)真金白銀的(de)虧損，交易者會比想象的(de)更脆弱、更容易懷疑策略的(de)開發中是否存在沒有考慮到的(de)問題（對(duì)于複雜(zá)策略更是如此）、自我動搖想要放棄這(zhè)個(gè)系統 —— 這(zhè)就是損失帶來(lái)的(de)主觀感受。

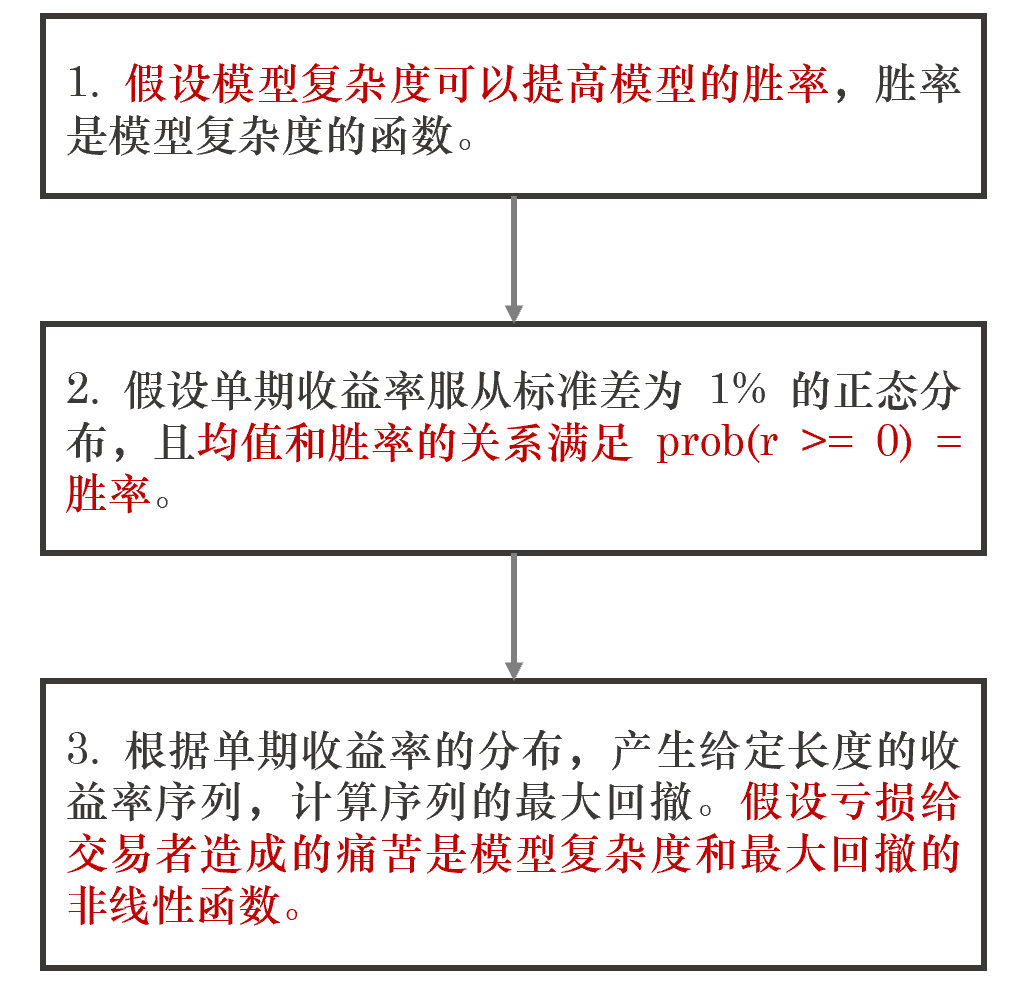
當一個(gè)策略持續出現回撤，虧損超過回測中最大(dà)回撤時(shí)，複雜(zá)度是否對(duì)虧損帶給我們的(de)痛苦程度（以及對(duì)策略不自信的(de)程度）造成影(yǐng)響呢(ne)？爲了(le)回答(dá)這(zhè)個(gè)問題，自然要建模。建模的(de)流程如下(xià)圖所示。

這(zhè)個(gè)流程中有三處需要建模：（1）模型複雜(zá)度和(hé)勝率的(de)關系；（2）勝率和(hé)收益率分(fēn)布均值的(de)關系；（3）模型複雜(zá)度和(hé)最大(dà)回撤與虧損造成的(de)痛苦的(de)關系。下(xià)面分(fēn)别說明(míng)。假設模型複雜(zá)度和(hé)勝率的(de)關系如下(xià)：

其中 w_0 是基礎勝率（假設等于 0.5），k 代表模型中參數的(de)個(gè)數，NL 爲 binary 變量，取值 0 或者 1，代表模型是否爲非線性的(de)（NL = 1 表示非線性）。Disclaimer：本模型沒有任何 reference，隻是我爲了(le)得(de)到量化(huà)分(fēn)析結果選用(yòng)的(de)一個(gè)簡單模型。假設單期收益率滿足标準差爲 1% 的(de)正态分(fēn)布，均值則和(hé)勝率有關。勝率代表著(zhe)單期收益率大(dà)于等于零的(de)概率，因此我們必須選擇均值以滿足 prob(r ≥ 0) = w。根據這(zhè)個(gè)關系，可(kě)以求出均值爲：

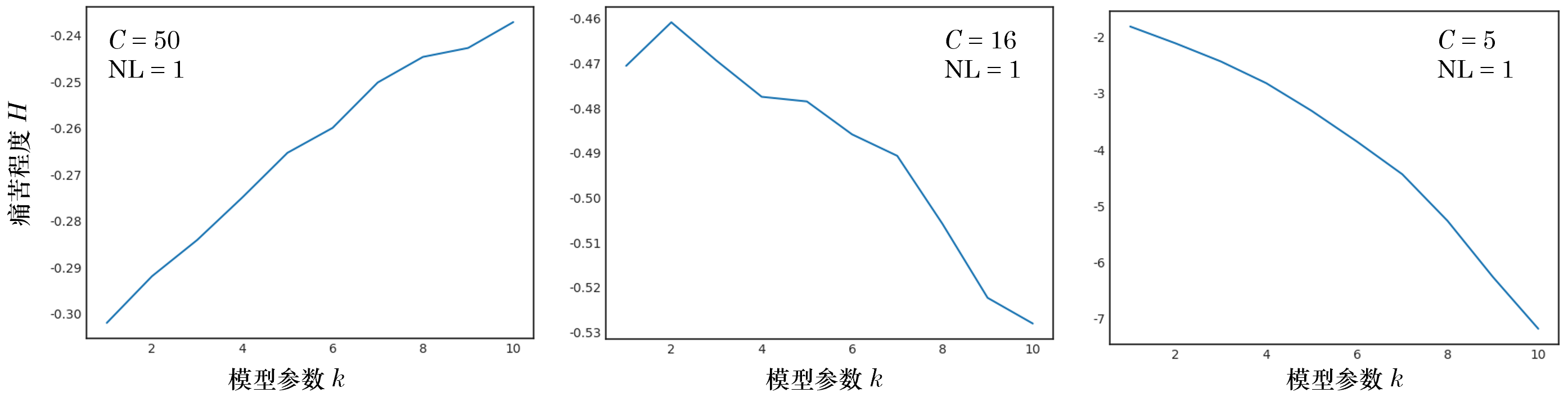
其中 ISF 表示标準正态分(fēn)布的(de) inverse survival function。得(de)到單期收益率的(de)分(fēn)布之後，就可(kě)以構建任意長(cháng)度的(de)收益率序列。分(fēn)析中，我們構建長(cháng)度爲 1000 的(de)序列，以此作爲該複雜(zá)度下(xià)假想策略的(de)收益曲率序列的(de)一個(gè)實現，并計算(suàn)出它的(de) NAV。有了(le) NAV 就可(kě)以計算(suàn)出它的(de)最大(dà)回撤（max drawdown，MDD）。假設虧損造成的(de)痛苦（記爲 H）和(hé)最大(dà)回撤以及模型複雜(zá)度的(de)關系如下(xià)：

上述模型（disclaimer：同樣沒有任何 reference）說明(míng) H 由兩部分(fēn)組成：模型複雜(zá)度和(hé)最大(dà)回撤。由該模型的(de)表達式可(kě)知，在同樣的(de)最大(dà)回撤下(xià)，不同的(de)模型複雜(zá)度給人(rén)的(de)主觀感受是不一樣的(de)，模型複雜(zá)度非線性的(de)放大(dà)了(le)虧損造成的(de)痛苦。當 k = 1（模型至少有一個(gè)參數）且模型爲非線性（NL = 0）時(shí)，H 的(de)第一項爲 1，因此它僅由最大(dà)回撤決定。當模型複雜(zá)度上升時(shí)，對(duì)複雜(zá)模型的(de)懲罰程度由參數 C（非負實數）控制。C 越小說明(míng)對(duì)模型複雜(zá)度的(de)懲罰越高(gāo)（即複雜(zá)模型會顯著放大(dà)最大(dà)回撤造成的(de)痛苦程度）。結合上述勝率和(hé)痛苦程度的(de)模型可(kě)知，模型複雜(zá)度可(kě)以增加勝率（hopefully），但它是以提高(gāo)虧損造成的(de)主觀痛苦爲代價的(de)。因此，在這(zhè)二者之間存在一個(gè)平衡。

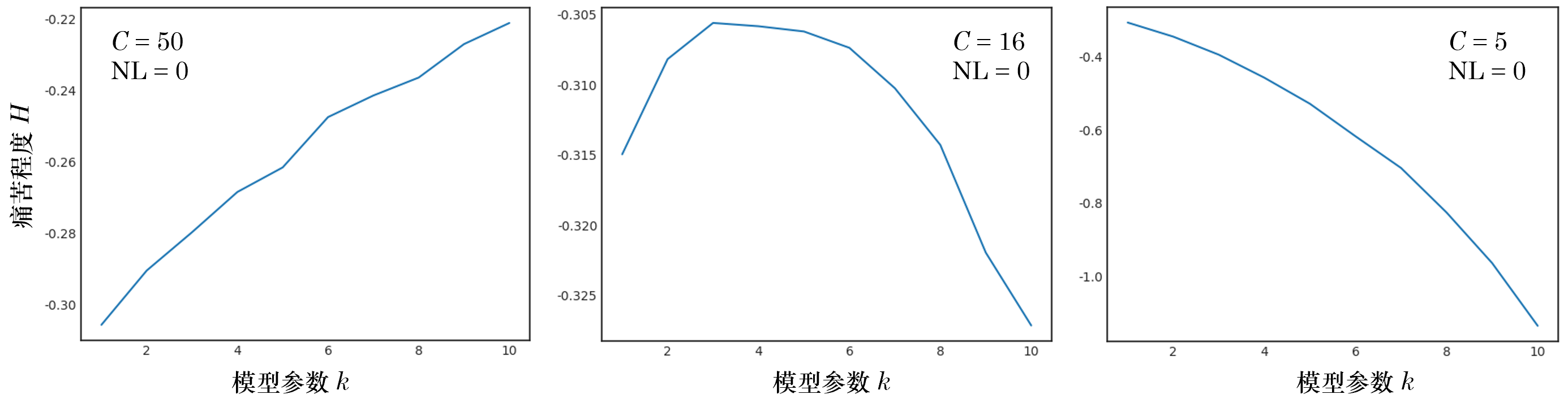
下(xià)面來(lái)看一些實驗結果。對(duì)于每一個(gè)給定的(de)模型複雜(zá)度，随機産生 2000 個(gè)長(cháng)度各爲 1000 的(de)收益率序列，并計算(suàn)它們的(de)最大(dà)回撤以及痛苦程度 H，取這(zhè) 2000 個(gè)實驗的(de)均值作爲該模型複雜(zá)度下(xià)損失造成的(de)痛苦程度的(de)度量。首先考慮線性模型，即 NL = 0 的(de)情況。下(xià)面三張圖分(fēn)别顯示了(le) C 取不同數值時(shí)，參數個(gè)數 k 和(hé) H 的(de)關系：

當 C 很大(dà)時(shí)，我們對(duì)模型複雜(zá)度的(de)懲罰很低，模型複雜(zá)度的(de)作用(yòng)單邊體現在提高(gāo)勝率上。更高(gāo)的(de)勝率意味著(zhe)更低的(de)最大(dà)回撤，因此随著(zhe)模型參數的(de)增加，痛苦程度逐漸降低。當 C 很小時(shí)，情況正好相反。模型每增加一個(gè)參數，造成的(de)痛苦程度非線性急速攀升，大(dà)大(dà)的(de)抵消掉高(gāo)勝率造成的(de)低回撤的(de)影(yǐng)響，痛苦程度随模型複雜(zá)度單調上升。當 C 取值中規中矩時(shí)，從上面中間的(de)圖中能夠觀察到勝率和(hé)痛苦程度之間的(de)取舍，在理(lǐ)論上存在最佳的(de)模型複雜(zá)度。當 NL = 1 時(shí)，可(kě)以觀察到和(hé)前面類似的(de)結果（下(xià)圖）。由于在 H 的(de)建模中，我們對(duì) NL 的(de)懲罰較高(gāo)（系數爲 10），因此對(duì)于同樣的(de) C 和(hé) k，NL = 1 比 NL = 0 意味著(zhe)更大(dà)的(de)虧損痛苦。

上面的(de)分(fēn)析都是探索性的(de)，并沒有實證數據作爲依據（難以找到使用(yòng)不同模型複雜(zá)度策略的(de)投資者并統計它們面對(duì)虧損時(shí)的(de)不同感受）。我分(fēn)析的(de)初衷是，在構建投資策略時(shí)，任何決定都要在得(de)與失之間取舍。複雜(zá)模型在提高(gāo)勝率的(de)同時(shí)，也(yě)一定在某種程度上有它的(de)弊端。從我有限的(de)經驗來(lái)說，在實盤中出現同樣程度的(de)虧損時(shí)，複雜(zá)的(de)模型比簡單的(de)模型更讓人(rén)不安。

在當下(xià)，我們越來(lái)越崇尚各種複雜(zá)的(de)模型。本小節僅僅希望從一個(gè)完全不同的(de)角度來(lái)提出一些思考：我們在樣本外是否 100% 做(zuò)好了(le)準備接受複雜(zá)模型？交易中存在各種認知偏差，如果我們連最簡單的(de)按一根均線做(zuò)趨勢追蹤都無法堅決的(de)執行，那又有什(shén)麽來(lái)保證我們在面對(duì)實盤虧損時(shí)能夠堅守複雜(zá)模型呢(ne)？如果我們不能堅守複雜(zá)模型，那麽開發複雜(zá)模型所付出的(de)心血和(hé)努力是否付之東流呢(ne)？

4 結語

前不久我聽(tīng)了(le) Vanguard 題爲《先鋒領航多(duō)資産 FOF 策略及外部管理(lǐ)人(rén)選聘概覽》的(de)報告。感觸最深的(de)是當談到對(duì)策略的(de)看法時(shí)，先鋒的(de)觀點是策略的(de)理(lǐ)念一定要簡單 —— 能用(yòng)一句話(huà)說清楚策略賺的(de)什(shén)麽錢，就不要用(yòng)兩句描述；策略的(de)程序一定要可(kě)理(lǐ)解、完全透明(míng)。

大(dà)道至簡。

各種複雜(zá)模型帶來(lái)的(de)邊際超額收益能否 justify 它們的(de)複雜(zá)度呢(ne)？拭目以待。

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。