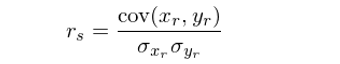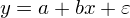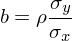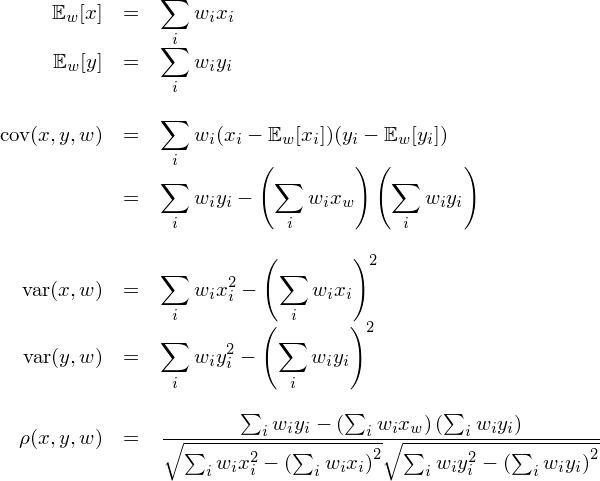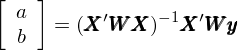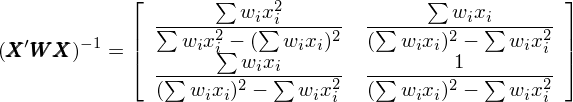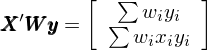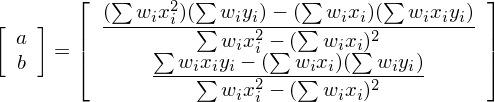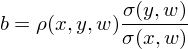用(yòng) IC 評價因子效果靠譜嗎？

作者：石川

摘要：傳統的(de) IC 或者 Rank IC 在評價因子選股效果時(shí)不夠合理(lǐ)，有一些陷阱。基于 IC 進行因子配置不十分(fēn)靠譜。本文提出對(duì) IC 的(de)一些改進，并建議(yì)使用(yòng)加權 IC 來(lái)評判因子效果。

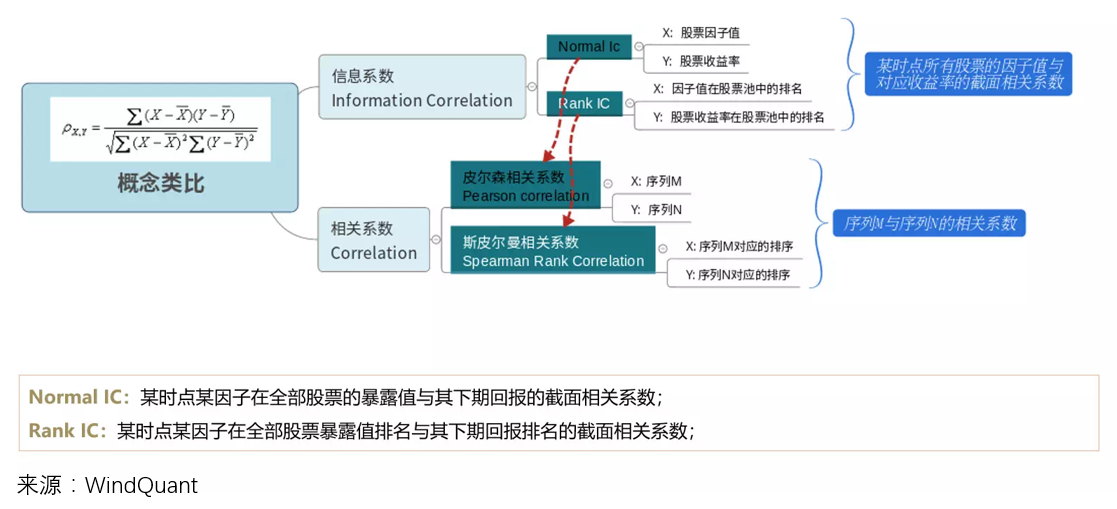
1 IC 和(hé) Rank IC

在多(duō)因子選股實務中，人(rén)們熱(rè)衷于動态評價因子在單期截面上的(de)選股效果。爲實現這(zhè)個(gè)目标，通(tōng)常的(de)做(zuò)法是用(yòng)當期個(gè)股的(de)因子取值（記爲 x）和(hé)下(xià)一期個(gè)股的(de)收益率（記爲 y）在截面上計算(suàn)信息系數（information correlation），簡稱 IC。IC 的(de)計算(suàn)方法通(tōng)常有兩種：x 和(hé) y 的(de)相關系數，以及 x 和(hé) y 的(de)秩相關系數（見下(xià)圖）。第一種就是我們常說的(de) IC，第二種可(kě)以稱作 Rank IC。

這(zhè)裏簡單介紹下(xià)秩相關系數。秩相關系數（rank correlation coefficient）和(hé)相關系數類似，不同的(de)是它考察的(de)是兩個(gè)随機變量之間的(de)單調相關性（monotonic correlation）。秩相關性對(duì)變量之間的(de)線性或非線性相關性不做(zuò)假設。在計算(suàn)秩相關系數時(shí)，使用(yòng)的(de)并不是觀測值本身的(de)數值，而是它們在各自樣本中的(de)排序。秩相關系數的(de)取值在 -1 到 1 之間。在統計學中，有多(duō)種計算(suàn)秩相關系數的(de)方法，其中最流行的(de)要數 Spearman 秩相關系數，它以 Charles Spearman 命名。假設有兩個(gè)随機變量 x 和(hé) y 的(de) n 對(duì)兒(ér)觀測值，Spearman 秩相關系數 r_s 的(de)計算(suàn)過程如下(xià)：

1. 首先将 x 和(hé) y 的(de)觀測值轉換成它們對(duì)應的(de)排序 x_r 和(hé) y_r。

2. 對(duì) x_r 和(hé) y_r 采用(yòng)傳統的(de)線性相關系數公式，則可(kě)得(de)到 r_s：

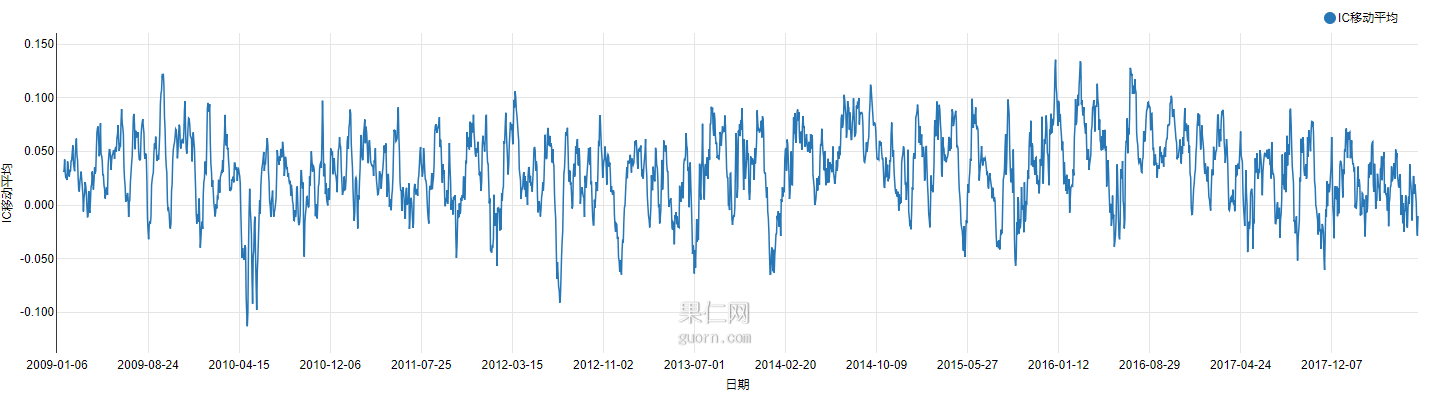
下(xià)圖是某因子在一段時(shí)間内的(de)滾動 Rank IC 移動平均，從中我們能對(duì)常見選股因子 IC 的(de)取值範圍有個(gè)大(dà)概的(de)了(le)解。

從上面的(de)定義可(kě)知，無論使用(yòng) IC 還(hái)是 Rank IC，都希望它越大(dà)越好，越大(dà)說明(míng)因子選股的(de)能力越強（也(yě)可(kě)以越小越好，那就反過來(lái)用(yòng)因子）。我們也(yě)經常能在一些策略中看到使用(yòng) IC（或者 IR，即 IC 的(de)均值除以标準差）的(de)高(gāo)低來(lái)動态進行因子的(de)配置。上面這(zhè)些用(yòng)法的(de)核心前提是 IC 能夠正确反映因子選股的(de)能力。然而，真的(de)是這(zhè)樣嗎？如果這(zhè)個(gè)核心前提不成立，那麽基于 IC 的(de)各種因子擇時(shí)、因子配置、因子打分(fēn)恐怕難言靠譜。

2 IC 中的(de)陷阱

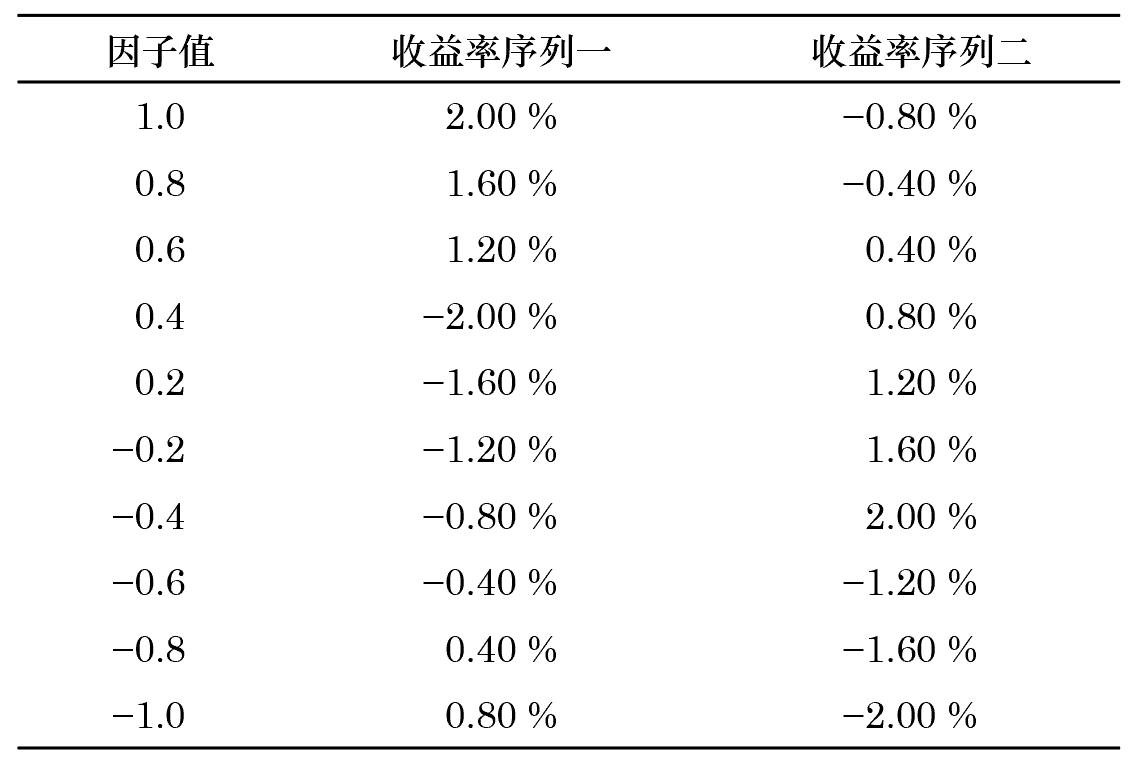
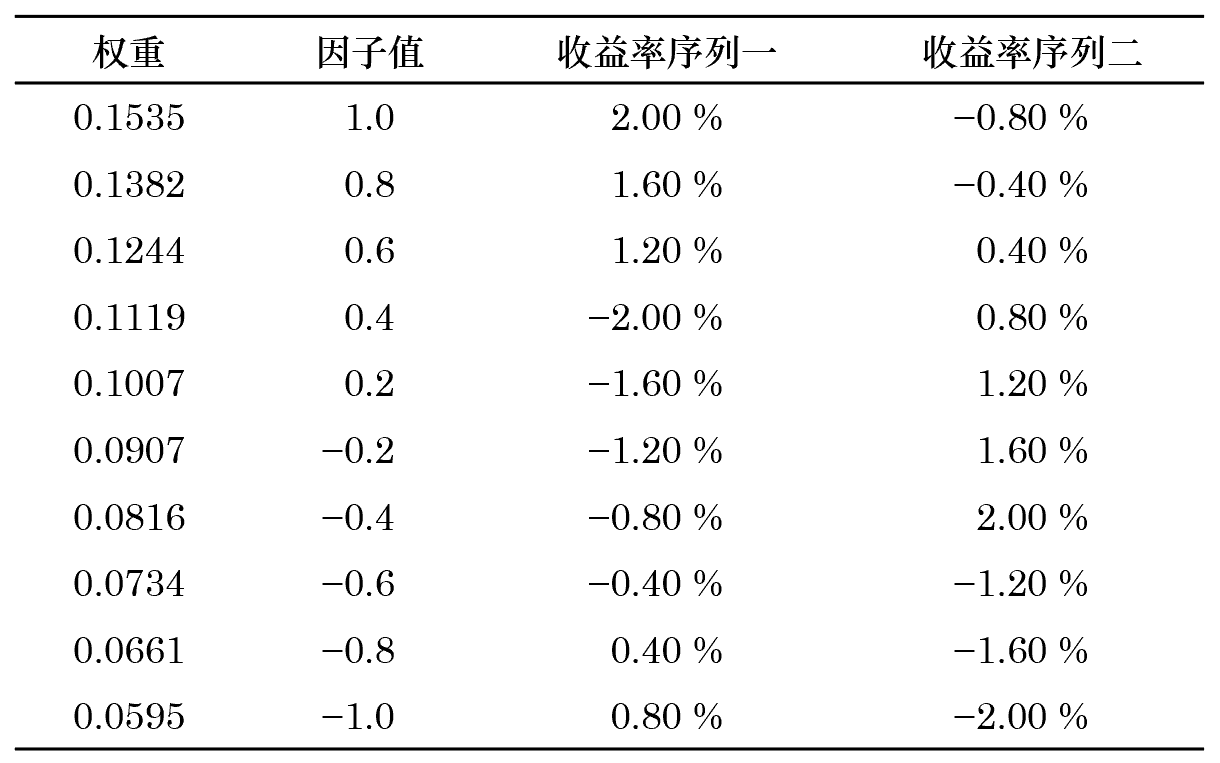
本節通(tōng)過一個(gè)假想的(de)例子說明(míng) IC 和(hé) Rank IC 計算(suàn)中存在的(de)陷阱。假設有十支股票(piào)，它們的(de)因子取值從大(dà)到小如下(xià)表所示。此外，考慮這(zhè)十支股票(piào)的(de)兩組假想的(de)收益率序列。

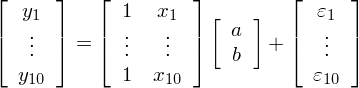
很容易計算(suàn)該因子和(hé)這(zhè)兩組收益率序列的(de)相關系數均爲 0.2909。如果僅僅看 IC 這(zhè)個(gè)單一指标的(de)話(huà)，我們會認爲該因子在當期的(de)選股能力很不錯。但 IC 背後還(hái)有很多(duō)故事可(kě)講。我們不妨把因子和(hé)這(zhè)兩組收益率序列畫(huà)出來(lái)，并各自做(zuò)一條線性回歸線來(lái)看一看。令 y 代表收益率，x 代表因子，則線性回歸模型表達式爲：

上式中斜率 b 和(hé) x 與 y 的(de)相關系數 ρ 滿足如下(xià)關系：

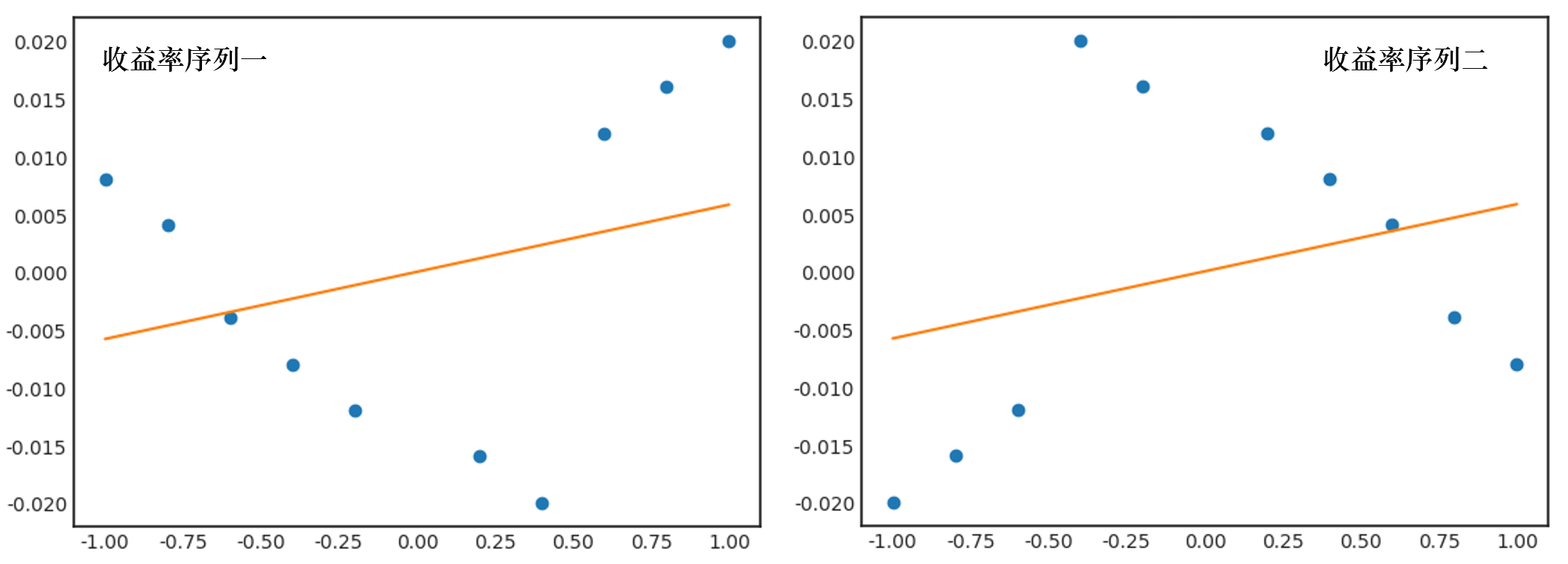
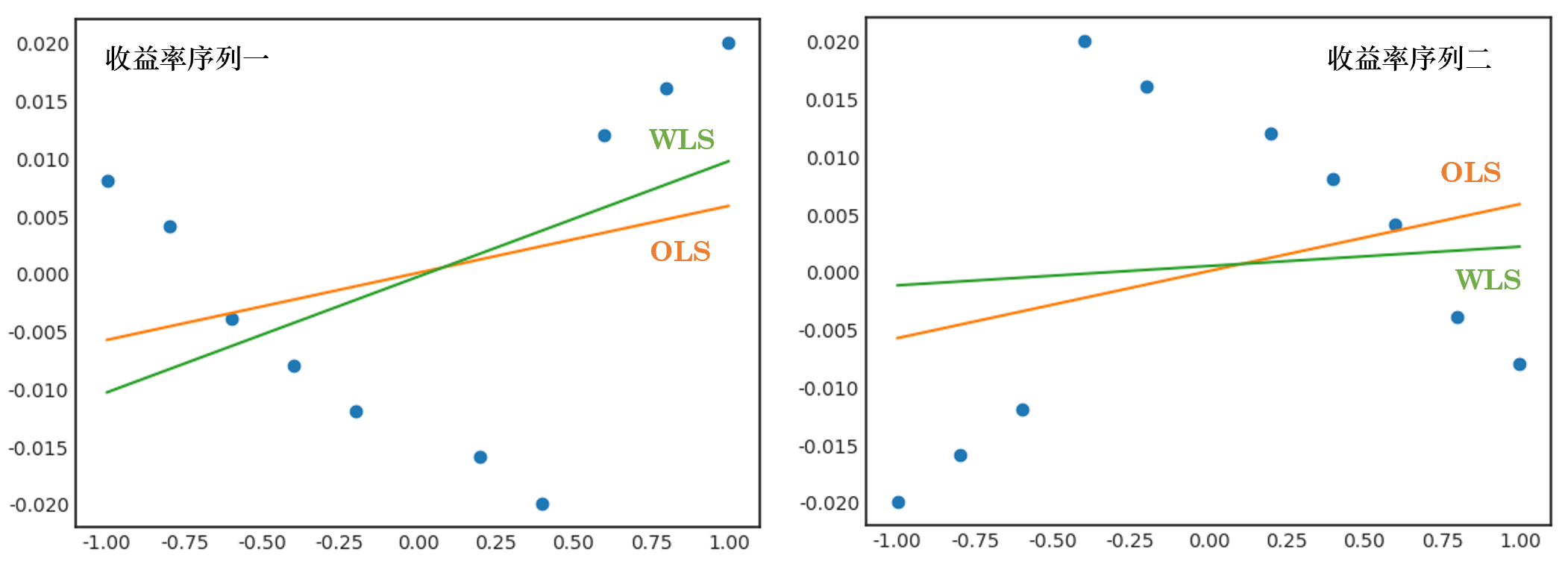
由于這(zhè)兩組收益率和(hé)因子的(de)相關系數均爲 0.2909，因此我們也(yě)以預期它們和(hé)因子的(de)線性回歸斜率相同。事實上，結果也(yě)正是如此（下(xià)圖，斜率均爲 0.0058）：

雖然 IC 一樣，但是畫(huà)出圖來(lái)才看到這(zhè)兩組收益率序列和(hé)因子的(de)關系大(dà)相徑庭。假設從業務邏輯來(lái)說，個(gè)股的(de)收益率和(hé)因子呈正相關，因此我們要選因子取值大(dà)的(de)股票(piào)。但是，這(zhè)個(gè)邏輯在上面兩組收益率序列中會得(de)到截然不同的(de)結果：對(duì)于序列一，使用(yòng)最大(dà)的(de)因子取值可(kě)以選出收益率最高(gāo)的(de)股票(piào)；而對(duì)于序列二，使用(yòng)最大(dà)的(de)因子取值卻選出了(le)收益率相當差的(de)股票(piào)。面對(duì)如此結果，IC 無辜嗎？如果使用(yòng) Rank IC 代替 IC，得(de)到的(de)也(yě)是同樣的(de)結論。這(zhè)兩組收益率和(hé)因子的(de)秩相關系數均等于 0.3212。從這(zhè)個(gè)數字背後解讀不出任何超過這(zhè)個(gè)數字本身的(de)東西。在量化(huà)投資中，我們喜歡并追尋能夠精确計算(suàn)出的(de)數字。但這(zhè)麽做(zuò)的(de)前提是該數字有意義。在統計學家中流傳著(zhe)一個(gè)說法：

Numerical calculations are exact, but graphs are rough.

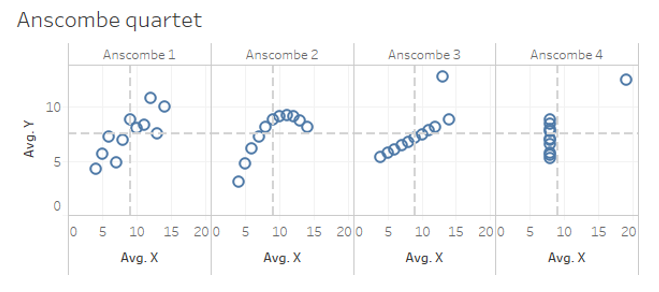
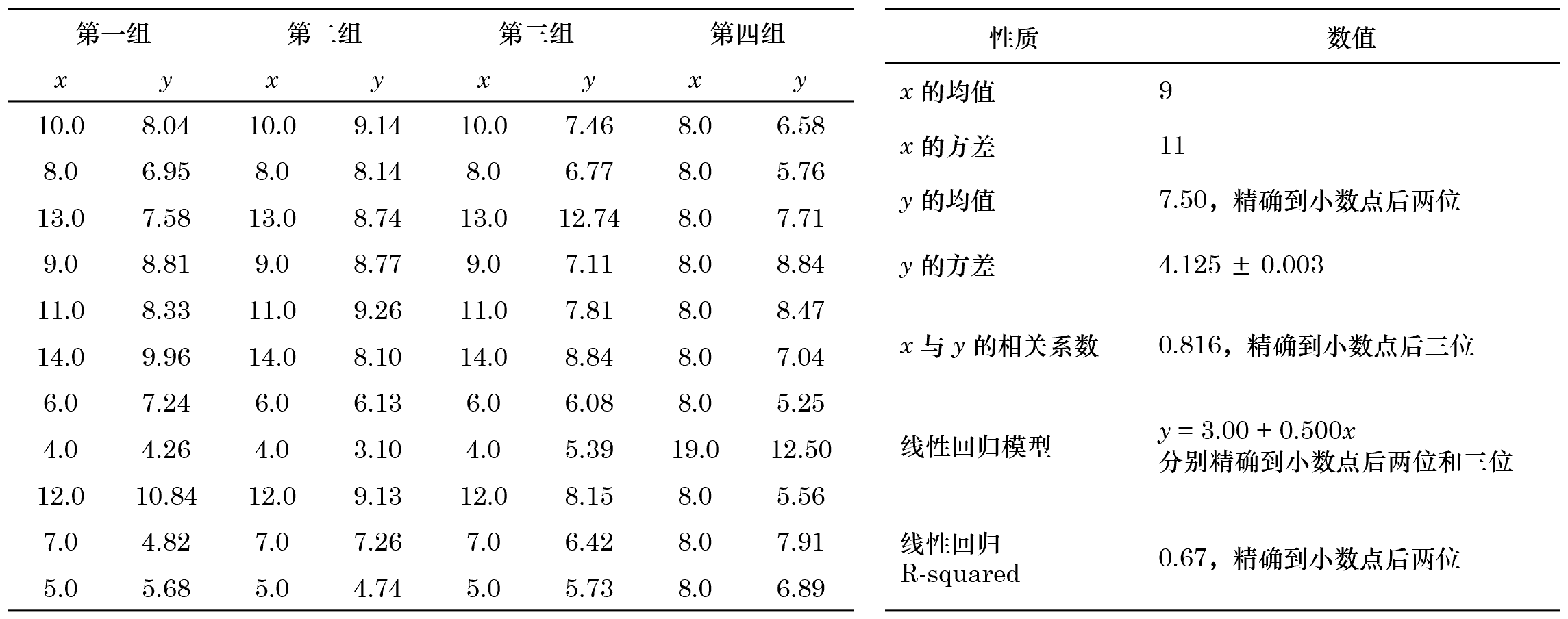
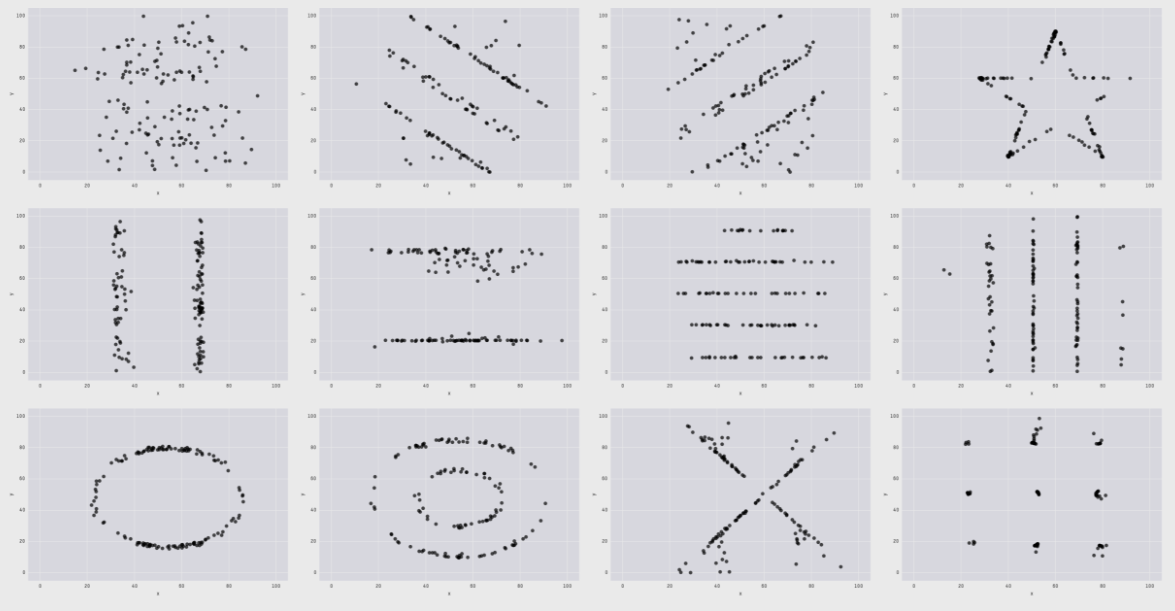
單一的(de)統計量，比如上面的(de) IC 或者 Rank IC 卻難以體現出圖形反映出來(lái)的(de)因子和(hé)收益率之間更多(duō)的(de)關系。這(zhè)說明(míng)如果我們僅僅看中 IC，可(kě)能會步入數據的(de)陷阱。僅關注統計量而忽視圖形信息本身最著名的(de)例子當屬安斯庫姆四重奏（Anscombe's quartet）。安斯庫姆四重奏是四組基本的(de)統計特性一緻的(de)數據，但由它們繪制出的(de)圖形則截然不同。每一組數據都包括了(le) 11 個(gè) (x, y) 點。這(zhè)四組數據由統計學家弗朗西斯·安斯庫姆（Francis Anscombe）于 1973 年構造，他(tā)的(de)目的(de)是用(yòng)來(lái)說明(míng)在分(fēn)析數據前先繪制圖表的(de)重要性，以及離群值對(duì)統計的(de)影(yǐng)響之大(dà)。下(xià)圖就是這(zhè)四組數據繪制出來(lái)的(de)圖形，可(kě)見它們截然不同：

這(zhè)四組數據和(hé)它們的(de)統計特征如下(xià)圖所示。這(zhè)個(gè)例子完美(měi)的(de)诠釋了(le)統計量（比如本文的(de) IC）不能反映出數據的(de)全部信息。更危險的(de)是，一旦它們被錯誤解讀和(hé)使用(yòng)，将會導緻完全錯誤的(de)結果。

3 改進 IC

上一節的(de)例子是爲了(le)說明(míng)當使用(yòng)個(gè)股的(de)因子取值和(hé)下(xià)期收益率在截面上回歸時(shí)，得(de)到的(de) IC 或者 Rank IC 不能很好的(de)反映出因子選股的(de)效果。對(duì)于這(zhè)種情況，可(kě)以考慮以下(xià)兩種改進方法。

第一種方法是按照(zhào)因子取值把個(gè)股分(fēn)成 n 檔（比如十檔），然後将每一檔視作一個(gè)投資組合，計算(suàn)投資組合收益率和(hé)投資組合因子在截面上的(de) IC 或 Rank IC。每一個(gè)投資組合中，可(kě)以按照(zhào)等權或者市值加權來(lái)計算(suàn)投資組合的(de)收益率和(hé)因子取值。因子描述的(de)是一攬子股票(piào)所共同承擔（或者暴露于的(de)）的(de)某一方面的(de)系統性風險。使用(yòng)因子選股是爲了(le)規避個(gè)股特異性收益率的(de)風險。因此，比起個(gè)股，我們更應該關注一攬子股票(piào)的(de)收益率和(hé)相應因子取值之間的(de)相關性。這(zhè)就是使用(yòng)因子構建投資組合、再計算(suàn) IC 的(de)初衷。投資組合的(de)收益率是一攬子股票(piào)的(de)均值，也(yě)可(kě)以更好的(de)消除收益率上的(de)噪聲。

第二種方法仍然從個(gè)股收益率和(hé)因子取值的(de) IC 出發，但是在計算(suàn)時(shí)根據因子的(de)業務邏輯（大(dà)到小、還(hái)是小到大(dà)的(de)關系）來(lái)給 x 和(hé) y 的(de)取值賦權，從而得(de)到 weighted IC。由于結合了(le)從業務邏輯出發的(de)權重，這(zhè)個(gè)加權 IC 能更好的(de)反映因子的(de)選股能力。下(xià)面以上一節的(de)因子取值和(hé)兩組收益率序列爲例解釋這(zhè)一做(zuò)法。假設從業務出發，因子取值越大(dà)越好。将十組 (x_i, y_i) 樣本點按照(zhào)因子值 x 從大(dà)到小排序，并假設它們的(de)權重按指數衰減，系數爲 0.9。這(zhè)十組樣本點的(de)權重爲：

有了(le)權重向量（記爲 w），就可(kě)以計算(suàn) x 和(hé) y 之間的(de)加權均值、加權方差、加權協方差、以及加權相關系數（weighted correlation coefficient）：

根據上述定義，很容易計算(suàn)出因子和(hé)這(zhè)兩組收益率序列的(de)加權相關系數。它們分(fēn)别爲 0.4494（因子和(hé)第一組收益率序列），以及 0.0908（因子和(hé)第二組收益率序列）。從加權 IC 來(lái)看，第一組的(de)收益率序列比第二組收益率序列更能說明(míng)因子的(de)選股能力。同樣的(de)，爲了(le)繪圖說明(míng)加入權重的(de)優勢，對(duì) x 和(hé) y 進行 weighted least squares 回歸（WLS）：

令 X 代表系數矩陣（包括截距項系數 1 和(hé) x），W 表示由權重 w_i 作爲第 i 個(gè)對(duì)角元素構成的(de)對(duì)角矩陣，則帶權重回歸的(de)解爲：

利用(yòng)線性代數的(de)運算(suàn)法則，不難求出上式右側的(de)第一項逆矩陣爲：

回歸式中右側第二項爲：

因此，加權回歸的(de)系數爲（其中 a 爲截距，b 爲斜率）：

費了(le)半天勁寫出了(le) a 和(hé) b 的(de)表達式（其實從求解的(de)角度，給出矩陣形式的(de)求解足夠了(le)）隻是想說明(míng)下(xià)面這(zhè)件事兒(ér)。如果我們比較加權相關系數 ρ(x, y, w) 以及加權方差（标準差）var(x, w) 和(hé) var(y, w)，以及斜率 b，則不難發現，和(hé) OLS 一樣，在加權回歸中，ρ 和(hé) b 仍然滿足如下(xià)關系：

下(xià)面就來(lái)畫(huà)圖比較一下(xià) WLS 回歸和(hé)上一節 OLS 回歸的(de)結果。對(duì)于這(zhè)兩組收益率序列，OLS 回歸的(de)結果相同。但從選股的(de)角度，我們知道如果因子對(duì)應的(de)是第一組收益率，則該因子遠(yuǎn)比其對(duì)應第二組收益率有效。但是 OLS 回歸（和(hé)普通(tōng)的(de) IC）無法體現這(zhè)一點。而采用(yòng)改進的(de) WLS（以及 weighted IC）來(lái)衡量的(de)話(huà)，如果因子産生了(le)第一組收益率序列，則它的(de) WLS 回歸斜率爲 0.01（大(dà)于 OLS 的(de)斜率 0.0058）；如果因子産生了(le)第二組收益率序列，則它的(de) WLS 回歸斜率僅爲 0.0017（小于 OLS 的(de)斜率）。這(zhè)說明(míng)通(tōng)過使用(yòng)基于因子業務規則的(de)權重系數，WLS 比 OLS 更能判斷因子和(hé)收益率之間的(de)關系。

4 結語

在我上統計課的(de)時(shí)候，教授總是反複強調，拿來(lái)數據先畫(huà)出來(lái)看一看。我們之所以能夠相信統計量，是以搞清楚了(le)數據内在的(de)結構、形态爲前提的(de)。如果沒有這(zhè)個(gè)前提，盲目的(de)相信統計量就會導緻錯誤的(de)判斷。金融數據已經信噪比極低了(le)，我們當然不希望因爲自己使用(yòng)不當再加入不必要的(de)噪聲。

很多(duō)時(shí)候數據關系越複雜(zá)，統計量傳遞出來(lái)的(de)信息可(kě)能越失真。

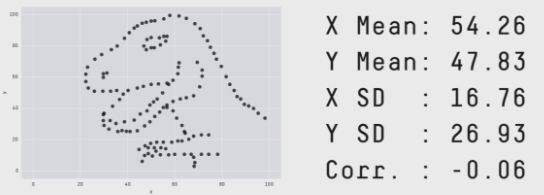
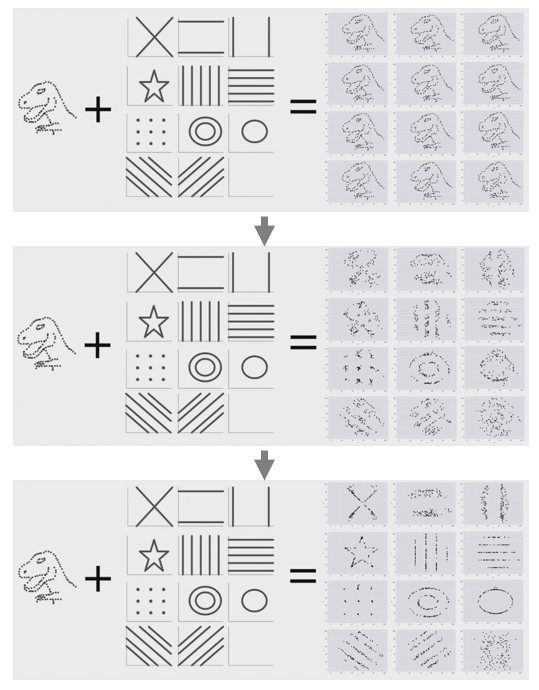
2017 年，來(lái)自 Autodesk Research 的(de) Matejka 和(hé)  Fitzmaurice 構建了(le)當代版的(de)“安斯庫姆四重奏”（Matejka and Fitzmaurice 2017）。他(tā)們用(yòng)計算(suàn)機算(suàn)法可(kě)以生成 x 均值、y 均值、x 标準差、y 标準差、以及 x 和(hé) y 相關系數相同的(de)複雜(zá)數據集。比如下(xià)圖中的(de) 12 個(gè)完全不同的(de)數據集就在上述五個(gè)統計量中取值完全一緻 —— x 均值 54.26，y 均值 47.83，x 标準差 16.76，y 标準差 26.93，x 和(hé) y 相關系數 -0.06。

先别忙著(zhe)驚訝，上述這(zhè)些數據集都是由下(xià)面這(zhè)張恐龍數據集（也(yě)有同樣的(de)統計量）構建來(lái)的(de)！

有的(de)朋友也(yě)許會說，IC 不夠，再引入更多(duō)的(de)統計量就行了(le)。我們當然可(kě)以計算(suàn)更高(gāo)階矩的(de)統計量，但是因爲數據的(de)信噪比極低，這(zhè)些樣本數據計算(suàn)出來(lái)的(de)高(gāo)階統計量也(yě)存在大(dà)量誤差。本文提出的(de)改進方法屬于從因子和(hé)收益率之間的(de)内在邏輯出發 —— 比如分(fēn)檔構建組合、或者給不同的(de)權重。這(zhè)些都是以内在的(de)邏輯爲先驗，以期更好的(de)判斷因子的(de)選股能力。如果你在使用(yòng) IC 或者 Rank IC（以及 IR）來(lái)動态的(de)評價、配置因子，那麽本文希望能引發你的(de)思考。在評價因子選股效果的(de)道路上，我們也(yě)許還(hái)有很長(cháng)的(de)路要走。

參考文獻

Matejka, J. and G. Fitzmaurice (2017). Same Stats, Different Graphs: Generating Datasets with Varied Appearance and Identical Statistics through Simulated Annealing. CHI 2017 Conference proceedings: ACM SIGCHI Conference on Human Factors in Computing Systems.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。