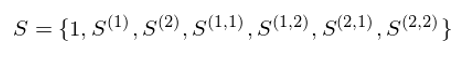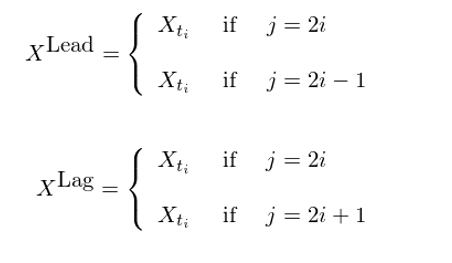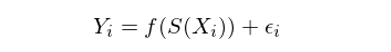粗糙路徑理(lǐ)論 —— 價格序列降維利器

作者：石川

摘要：粗糙路徑理(lǐ)論通(tōng)過路徑簽名可(kě)有效對(duì)原始價格信息降維，使用(yòng)它作爲有監督學習(xí)的(de)特征輸入可(kě)以取得(de)更好的(de)效果。

1 引言

機器學習(xí)中的(de)有監督學習(xí)算(suàn)法時(shí)常被用(yòng)來(lái)預測投資品的(de)價格走勢。以此爲目的(de)建模時(shí)，訓練集數據的(de)特征（features）選擇格外重要。我們希望找到最能捕捉價格走勢的(de)特征，但如果特征維數太高(gāo)又容易造成過拟合以及計算(suàn)效率的(de)問題。當直接使用(yòng)投資品的(de)價格信息作爲輸入時(shí)，訓練出來(lái)的(de)模型效果往往很差，這(zhè)是因爲價格信息的(de)維數太高(gāo)了(le)。

以日線爲例，假如我們想使用(yòng)過去 n 個(gè)交易日的(de)日頻(pín) K 線建模，預測下(xià)一個(gè)交易日的(de)漲跌。由于每個(gè) K 線有 Open、High、Low 和(hé) Close 四個(gè)價格，那麽這(zhè) n 個(gè) K 線的(de)輸入維數就是 4n。當 n = 20 時(shí)，這(zhè)個(gè)模型的(de)輸入維數就高(gāo)達 80。如果我們采用(yòng)非線性的(de)有監督學習(xí)算(suàn)法（比如非線性核的(de)支持向量機），那麽維數更會呈指數增長(cháng)。使用(yòng)如此多(duō)的(de)特征建模，樣本内很容易出現過拟合，模型在樣本外的(de)預測準确性會非常低。在構建這(zhè)類模型時(shí)，對(duì)輸入特征的(de)有效降維至關重要。我們熟悉的(de)各種技術指标其實就是降維。技術指标對(duì)價格數據高(gāo)度提煉、降噪，以期捕捉到一些更泛化(huà)的(de)信息。基于技術指标的(de)技術分(fēn)析策略能賺錢說明(míng)使用(yòng)技術指标降維可(kě)以在一定程度上捕捉價格運動的(de)内在規律。

今天我們就來(lái)介紹另一種捕捉價格走勢内在規律的(de)方法 —— 粗糙路徑理(lǐ)論（rough path theory）。它的(de)本質是通(tōng)過計算(suàn)路徑簽名（signature of a path）來(lái)對(duì)路徑的(de)信息降維，并使用(yòng)簽名代替路徑本身作爲機器學習(xí)模型的(de)輸入特征。本文就來(lái)揭開它神秘的(de)面紗。

2 粗糙路徑理(lǐ)論

粗糙路徑理(lǐ)論發展自上世紀 90 年代（Lyons 1998）。顧名思義，它研究的(de)對(duì)象是粗糙路徑（rough path）。這(zhè)裏，“粗糙”指的(de)是路徑雖然連續，但是處處劇烈波動。比如布朗運動産生的(de)路徑就是“粗糙的(de)”，它雖然連續但是處處不可(kě)微分(fēn)。投資品的(de)價格走勢可(kě)謂名副其實的(de)粗糙路徑。在粗糙路徑理(lǐ)論中，最核心的(de)概念就是路徑簽名。這(zhè)個(gè)“簽名”就是一個(gè)映射函數（mapping），它将原始路徑信息轉換成一組實數集合。集合中的(de)每一個(gè)實數都是通(tōng)過原始路徑中的(de)數據點以不同的(de)方式計算(suàn)而來(lái)，代表著(zhe)原始路徑的(de)某一個(gè)幾何特征。理(lǐ)論上，一個(gè)路徑的(de)簽名是“無窮維”的(de)。在實際使用(yòng)中，我們隻使用(yòng)有限個(gè)維數的(de)簽名（即實數集合中的(de)實數個(gè)數有限），這(zhè)樣的(de)簽名稱爲截斷簽名（truncated signature）。使用(yòng)截斷簽名來(lái)代替原始高(gāo)維路徑的(de)數據信息便是對(duì)其進行降維。

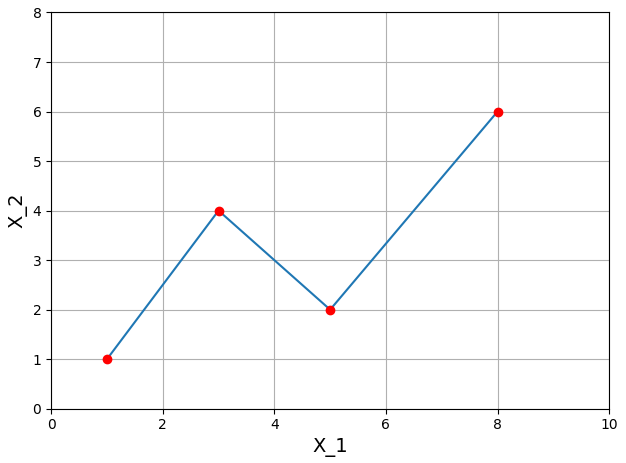
計算(suàn)粗糙路徑的(de)（截斷）簽名需要用(yòng)到張量代數（Tensor algebra），十分(fēn)複雜(zá)，本文不加贅述。假設原始路徑是 n × N 維的(de)，它的(de)簽名是通(tōng)過将這(zhè)個(gè)路徑不斷的(de)向其原始的(de) n 維坐(zuò)标系上投影(yǐng)得(de)到的(de)。下(xià)面以 n = 2 爲例說明(míng)如何求解一個(gè)路徑的(de)（截斷）簽名。假設一個(gè)二維粗糙路徑如下(xià)圖所示。

它的(de) 2 階截斷簽名 S 是由 7 個(gè)實數構成的(de)集合：

這(zhè) 7 個(gè)實數的(de)幾何意義總結如下(xià)：

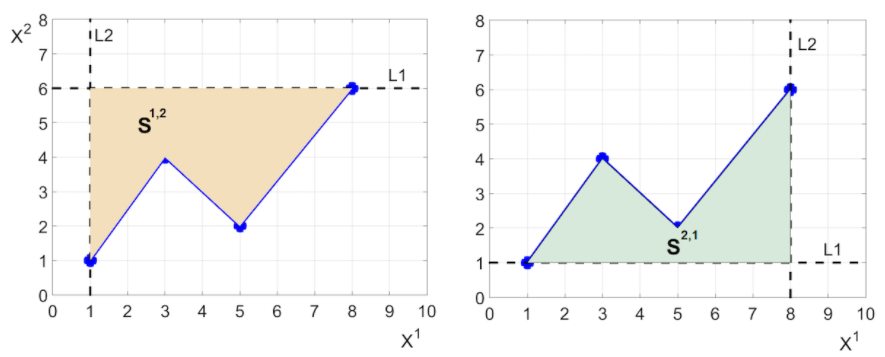
其中，S^(1,2) 和(hé) S^(2,1) 表示該路徑按特定形式與坐(zuò)标軸構成的(de)區(qū)域的(de)面積，如下(xià)圖所示。

用(yòng)一句話(huà)總結來(lái)說，這(zhè)個(gè) 2 階截斷簽名中的(de) 7 個(gè)數每個(gè)都有明(míng)确的(de)幾何含義，并且由原始粗糙路徑計算(suàn)而來(lái)；這(zhè) 7 個(gè)數構成的(de)簽名是對(duì)原始路徑信息的(de)高(gāo)度概括。當我們用(yòng)簽名代替原始路徑作爲輸入特征時(shí)，一個(gè)必須要搞清楚的(de)前提是：簽名和(hé)路徑是一一對(duì)應的(de)嗎？路徑可(kě)以有千千萬萬，如果不同的(de)路徑有相似的(de)簽名，那麽用(yòng)簽名代替路徑的(de)效果就要打折扣了(le)。另外，不要忘了(le)，我們使用(yòng)的(de)是截斷簽名中，它更是舍棄了(le)高(gāo)階的(de)信息。即便非截斷簽名和(hé)路徑一一對(duì)應，截斷簽名又是否能很好的(de)描述原始路徑呢(ne)？好消息是，數學上可(kě)以證明(míng)粗糙路徑的(de)簽名是唯一的(de)，因此簽名很好的(de)反應了(le)原始路徑的(de)信息。那麽，截斷簽名怎麽樣呢(ne)？事實上，高(gāo)階簽名所包含的(de)信息量按照(zhào)階數的(de)階乘衰減（factorial decay）。這(zhè)意味著(zhe)高(gāo)階簽名包含的(de)信息較低階簽名來(lái)說可(kě)以忽略不計，因此即便是使用(yòng)低階的(de)截斷簽名，我們也(yě)可(kě)以預期它有效的(de)保留了(le)原始路徑的(de)信息。在上面這(zhè)個(gè)例子當中，原始的(de)路徑就可(kě)以由它的(de)截斷簽名 {1, 7, 5, 24.5, 19, 16, 12.5} 表示。

3 領先 —— 滞後變形

截斷簽名是對(duì)原始粗糙路徑的(de)有效降維。這(zhè)爲我們使用(yòng)它進行投資品價格數據分(fēn)析打下(xià)了(le)良好的(de)基礎。不過在這(zhè)之前，還(hái)需要做(zuò)一步鋪墊。投資品的(de)價格時(shí)間序列對(duì)原始“未知路徑”按一種特定頻(pín)率的(de)采樣。當使用(yòng)最高(gāo)頻(pín)率采樣時(shí)，得(de)到的(de)就是 tick 數據；當使用(yòng) 1 分(fēn)鐘(zhōng)頻(pín)率采樣時(shí)，得(de)到的(de)就是 1 分(fēn)鐘(zhōng) K 線數據；當使用(yòng)日頻(pín)采樣時(shí)，得(de)到的(de)就是日頻(pín) K 線數據，以此類推。換句話(huà)說，我們的(de)價格數據僅僅是一些列來(lái)自未知路徑的(de)離散點，它們并不是連續的(de)。粗糙路徑雖然處處高(gāo)波動，但它是連續的(de)。因此，在使用(yòng)簽名分(fēn)析價格時(shí)，必須先将離散的(de)價格時(shí)間序列轉化(huà)爲連續的(de)路徑。

在這(zhè)方面，一個(gè)常見的(de)方法是領先 —— 滞後變形（lead-lag transformation）。假設 t_0，t_1，…，t_N 爲 N 個(gè)離散時(shí)間點，定義在之上的(de)價格序列爲 {t_i, X_(t_i)}, i = 0，1，…，N，該變形的(de)定義如下(xià)：

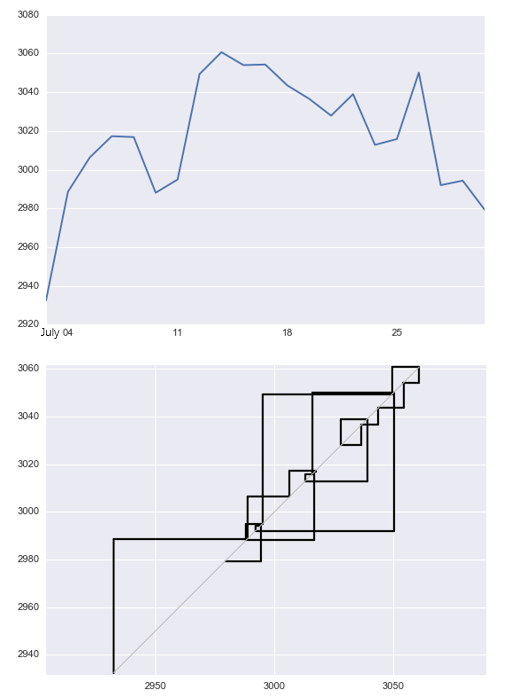
從圖形上直觀的(de)來(lái)說，該變形将原來(lái)長(cháng)度爲 N + 1（0 到 N）的(de)價格序列轉變爲長(cháng)度爲 2N + 1（0 到 2N）的(de)新序列。在這(zhè)個(gè)新序列中，每個(gè)點由一對(duì)兒(ér)領先價格（X^Lead）和(hé)滞後價格（X^Lag）來(lái)表示。在這(zhè)個(gè)新序列中的(de)第 0，2，…，2N 這(zhè)些序列标号爲偶數的(de)點上，X^Lead 和(hé) X^Lag 的(de)取值就是原始序列中的(de) X_{j/2}；在這(zhè)個(gè)新序列中的(de)第 1，3，…，2N - 1 這(zhè)些序列标号爲奇數的(de)點上，第 j（某奇數）個(gè)點的(de) X^Lead 取值等于第 j + 1 個(gè)點的(de) X^Lead 值，而它的(de) X^Lag 取值等于第 j - 1 個(gè)點的(de) X^Lag 值。如果我們比較這(zhè) 2N 個(gè)點的(de) X^Lead 和(hé) X^Lag 序列，不難發現 X^Lag 永遠(yuǎn)比 X^Lead 落後一位；這(zhè)便解釋了(le)爲什(shén)麽它們有“領先”和(hé)“滞後”之分(fēn)。這(zhè) 2N 個(gè)由 {X^Lead, X^Lag} 兩兩配對(duì)兒(ér)構成的(de)新序列就是對(duì)原始離散價格時(shí)間序列的(de)連續化(huà)處理(lǐ)，将其轉化(huà)爲一個(gè)連續的(de)路徑。下(xià)圖爲上證指數在 2016 年 7 月(yuè)内收盤價的(de)日數據和(hé)通(tōng)過領先 —— 滞後變形産生的(de)連續路徑。

爲什(shén)麽要采用(yòng)如此變化(huà)得(de)到路徑呢(ne)？對(duì)于投資品價格這(zhè)種粗糙路徑來(lái)說，由于其劇烈的(de)波動，它的(de)二次變分(fēn)不爲零，這(zhè)個(gè)數學上的(de)特性反映著(zhe)價格變化(huà)中非常重要的(de)性質（見《布朗運動、伊藤引理(lǐ)、BS 公式（前篇）》）。因此，我們希望路徑簽名也(yě)能反映原始軌迹非零二次變分(fēn)的(de)特征。通(tōng)過領先 —— 滞後變形得(de)到的(de)路徑，并計算(suàn)其簽名，就可(kě)以很好的(de)捕捉到原始價格序列的(de)二次變分(fēn)。好了(le)，現在我們已經萬事俱備了(le)：對(duì)于一個(gè)投資品價格序列，首先應用(yòng)領先 —— 滞後變形将其轉換爲連續路徑；然後計算(suàn)截斷簽名對(duì)該路徑降維；最後使用(yòng)該簽名作爲特征輸入到機器學習(xí)算(suàn)法中建模。下(xià)面就來(lái)看一個(gè)簡單的(de)應用(yòng)。

4 應用(yòng)舉例

本節介紹一個(gè)使用(yòng)路徑簽名分(fēn)析價格規律的(de)例子。我們的(de)目的(de)并非構建一個(gè)策略，而是爲了(le)說明(míng)路徑簽名确實能夠反應出價格的(de)某些内在規律。A 股中有不同的(de)闆塊，雖然不同的(de)闆塊在絕大(dà)多(duō)數時(shí)候相關度非常高(gāo)，但是在某些特定的(de)時(shí)期還(hái)是存在明(míng)顯的(de)分(fēn)化(huà)。比如在 2013 年，創業闆就走出了(le)獨立行情。因此，我們猜測在這(zhè)個(gè)時(shí)間内，屬于創業闆的(de)股票(piào)的(de)價格和(hé)其他(tā)版塊的(de)股票(piào)的(de)價格就有不同的(de)内在規律。下(xià)面就來(lái)簡單驗證看看。

考慮來(lái)自上交所和(hé)創業闆的(de) 356 支股票(piào)（其中上交所 220 支，創業闆 136 支），使用(yòng)它們在 2013 年 1 月(yuè) 1 日到 2014 年 1 月(yuè) 1 日期間的(de)日數據作爲各自的(de)原始價格序列（用(yòng)各自的(de)最大(dà)值進行标準化(huà)）。經過領先 —— 滞後變形後得(de)到各自的(de)連續路徑，并選擇階數 3 計算(suàn)路徑簽名（簽名維數爲 14）。之後，将這(zhè) 356 支股票(piào)打亂順序，随機挑選 220 支作爲訓練集，剩餘 136 支作爲測試集。我們希望通(tōng)過訓練集構建一個(gè)分(fēn)類模型。該分(fēn)類模型使用(yòng)訓練集中股票(piào)的(de)路徑簽名作爲輸入，以股票(piào)的(de)出處（即上交所或創業闆）作爲标簽，挖掘輸入和(hé)标簽之間的(de)關系：

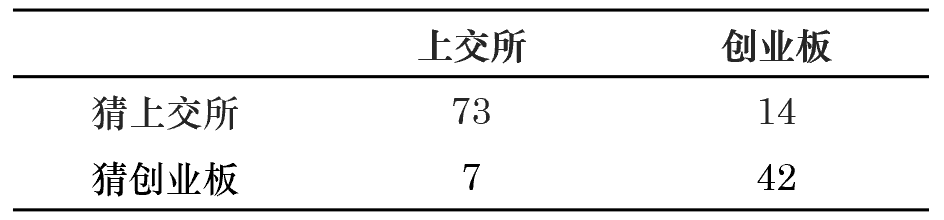
其中 Y_i 是第 i 支股票(piào)的(de)标簽，X_i 是第 i 支股票(piào)的(de)原始價格序列，S(X_i) 是它的(de)路徑簽名，f 則是我們希望通(tōng)過機器學習(xí)拟合出來(lái)的(de)函數。數學上的(de)相關定理(lǐ)（Levin et al. 2016）指出，線性方程就可(kě)以很好的(de)滿足我們的(de)目标，因此在本例中我們采用(yòng)線性回歸作爲機器學習(xí)的(de)算(suàn)法。使用(yòng)訓練集的(de) 220 支股票(piào)建模。之後，使用(yòng)該模型對(duì)測試集中的(de) 136 支股票(piào)分(fēn)類，并将模型分(fēn)類結果和(hé)真實類别比較。該判斷該模型在樣本外的(de)準确性爲 84.56%。讓我們從準确率和(hé)召回率兩方面進一步評價。該模型在測試集上的(de)分(fēn)類結果如下(xià)表所示。

從上面的(de)結果可(kě)知，對(duì)于猜上交所的(de)預測來(lái)說，其準确率爲 83.90%，召回率爲 91.25%；對(duì)于猜創業闆的(de)預測來(lái)說，其準确率爲 85.71%，召回率爲 75%。可(kě)見，對(duì)于這(zhè)兩類股票(piào)中，該模型在樣本外均有不錯的(de)表現。這(zhè)說明(míng)使用(yòng)路徑簽名有效的(de)捕捉了(le)不同闆塊中股票(piào)價格的(de)内在運動規律，它作爲機器學習(xí)算(suàn)法的(de)輸入是合适的(de)。

5 結語

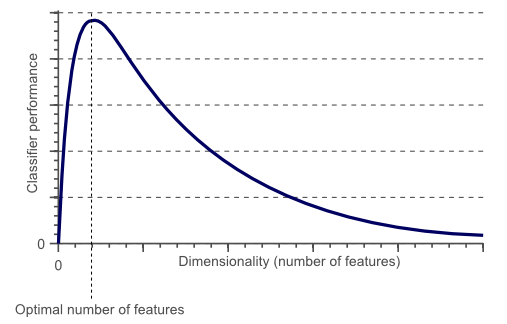
本文介紹了(le)粗糙路徑理(lǐ)論及其在分(fēn)析投資品價格走勢方面的(de)應用(yòng)。對(duì)于一個(gè)成功的(de)機器學習(xí)應用(yòng)來(lái)說，找尋合适的(de)輸入特征是最重要的(de)一步。特征的(de)維數不能過高(gāo)，且需要最大(dà)可(kě)能的(de)保存原始數據的(de)信息。舉例來(lái)說，如果我們想建模對(duì)人(rén)的(de)性别進行分(fēn)類，我們可(kě)以采用(yòng)任何和(hé)人(rén)相關的(de)屬性，比如身高(gāo)或者膚色。顯然，身高(gāo)就比膚色更有效，因爲男(nán)性較女(nǚ)性更高(gāo)，但每個(gè)膚色中的(de)男(nán)女(nǚ)比例都差不多(duō)。在當下(xià)流行人(rén)工智能卷積神經網絡中，池化(huà)（pooling）就是爲了(le)減少特征的(de)維數。在分(fēn)類領域，有一個(gè)著名的(de)概念叫做(zuò)維數災難（curse of dimensionality）：分(fēn)類器的(de)性能随著(zhe)特征個(gè)數的(de)變化(huà)不斷增加，過了(le)某一個(gè)值後，性能不升反降（下(xià)圖，橫坐(zuò)标是維數，縱坐(zuò)标是分(fēn)類器的(de)表現）。

對(duì)于分(fēn)析價格序列來(lái)說，如何給數據降維自然是重中之重。粗糙路徑的(de)截斷簽名通(tōng)過有限個(gè)具備明(míng)确幾何意義的(de)實數，有效的(de)捕捉了(le)原始序列的(de)信息、降低了(le)特征的(de)維數，這(zhè)是它對(duì)于後續機器學習(xí)建模的(de)最大(dà)價值。

參考文獻

Levin, D., T. Lyons, and H. Ni (2016). Learning from the past, predicting the statistics for the future, learning an evolving system. Working paper.

Lyons, T. (1998). Differential equations driven by rough signals. Revista Matemática Iberoamericana 14(2), 215 – 310.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。