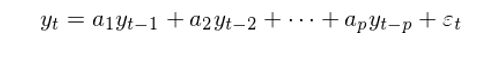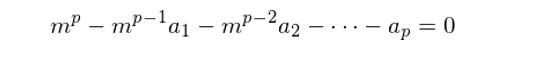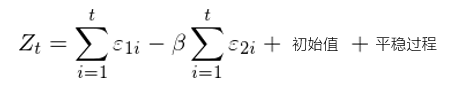小心僞回歸發現的(de)假關系
發布時(shí)間:2018-02-27 | 來(lái)源: 川總寫量化(huà)
作者:石川
摘要:回歸分(fēn)析在量化(huà)投資中的(de)應用(yòng)十分(fēn)廣泛。但是金融時(shí)間序列中有很多(duō)不滿足平穩性,我們必須警惕它們造成的(de)僞回歸。
1 生活中随處可(kě)見的(de)僞回歸
回歸分(fēn)析在量化(huà)投資中的(de)應用(yòng)十分(fēn)廣泛。比如在選股或者預測股票(piào)收益率時(shí),人(rén)們常常使用(yòng)宏觀經濟數據或公司基本面數據等對(duì)收益率回歸,以期找出能夠解釋收益率的(de)自變量(又稱爲因子)。由于金融數據之間的(de)關系大(dà)多(duō)爲線性,因此線性回歸往往就足夠用(yòng)了(le);而因爲線性回歸又足夠簡單,這(zhè)就使得(de)回歸分(fēn)析更加普及。
回歸分(fēn)析的(de)目的(de)是爲了(le)找到自變量和(hé)因變量之間的(de)相關性。然而,當我們對(duì)時(shí)間序列進行回歸分(fēn)析時(shí),必須要警惕一類陷阱,它就是僞回歸(spurious regression),它指的(de)是自變量和(hé)因變量之間本來(lái)沒有任何因果關系,但由于某種原因,回歸分(fēn)析卻顯示出它們之間存在統計意義上的(de)相關性,讓人(rén)錯誤地認爲兩者之間有關聯,這(zhè)種相關性稱作僞關系(spurious relationship)。
僞回歸在生活中随處可(kě)見,來(lái)看下(xià)面兩個(gè)例子。
例子一:冰淇淋銷量和(hé)溺水(shuǐ)兒(ér)童數
某個(gè)夏天,人(rén)們發現鎮上的(de)冰淇淋銷量和(hé)溺水(shuǐ)兒(ér)童數量同步上升。如果拿冰淇淋銷量對(duì)溺水(shuǐ)兒(ér)童數量進行線性回歸,得(de)到的(de)結論是前者是後者的(de)一個(gè)很好的(de)解釋變量。但從現實生活中的(de)邏輯來(lái)看,這(zhè)兩者應該有所謂的(de)“冰淇淋賣得(de)好,溺水(shuǐ)兒(ér)童數就多(duō)”的(de)關系嗎?這(zhè)是否意味著(zhe)“遊泳池的(de)兒(ér)童都在吃(chī)冰淇淋”?正确的(de)答(dá)案是,這(zhè)僅僅是一個(gè)僞回歸(下(xià)一節會解釋成因)。
例子二:居民消費和(hé)鸬鹚個(gè)數
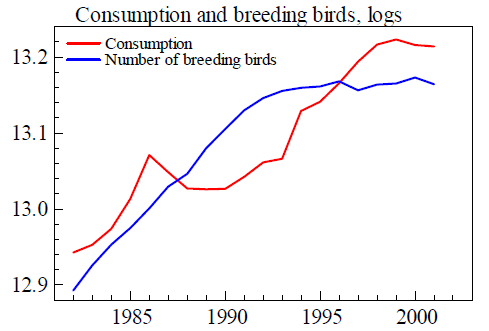
下(xià)圖來(lái)自真實的(de)數據,兩條曲線代表的(de)時(shí)間序列分(fēn)别爲丹麥居民消費的(de)對(duì)數(紅線)以及該國飼養鸬鹚數量的(de)對(duì)數(藍線)。從圖中來(lái)看,它們顯然非常相關。如果用(yòng)紅線對(duì)藍線回歸,得(de)到的(de)回歸系數顯著不爲 0,且回歸的(de) R-squared 高(gāo)達 0.688,說明(míng)藍線對(duì)紅線的(de)解釋能力非常強。但這(zhè)顯然也(yě)是毫無意義的(de)(因爲居民消費和(hé)鸬鹚個(gè)數之間沒有任何有邏輯的(de)關聯),它同樣來(lái)自僞回歸(成因和(hé)例子一不同)。
本文就來(lái)介紹僞回歸。了(le)解如何識别它,才能避免在構建量化(huà)模型時(shí)錯誤的(de)使用(yòng)不同數據之間的(de)僞關系。
2 成因和(hé)數學特性
僞回歸的(de)成因一般有兩個(gè)。在上一節的(de)第一個(gè)例子中,僞回歸的(de)成因是存在幹擾因素(confounding factor,或稱潛在變數 lurking variable)。在第二個(gè)例子中,僞回歸的(de)成因是兩個(gè)變量之間的(de)局部随機趨勢(local stochastic trend)。當兩個(gè)變量同時(shí)受第三個(gè)因素影(yǐng)響時(shí),這(zhè)兩個(gè)變量間可(kě)能存在誤導性的(de)相關性,這(zhè)第三個(gè)因素稱爲幹擾因素。在第一個(gè)例子中,幹擾因素是夏天炎熱(rè)的(de)高(gāo)溫。高(gāo)溫造成了(le)冰淇淋銷量的(de)上升;此外高(gāo)溫也(yě)使得(de)更多(duō)的(de)兒(ér)童去公共泳池從而造成溺水(shuǐ)事故增多(duō)。高(gāo)溫是造成冰淇淋銷量和(hé)溺水(shuǐ)兒(ér)童數上升的(de)共同因素;這(zhè)兩者本身之間并沒有相關性。
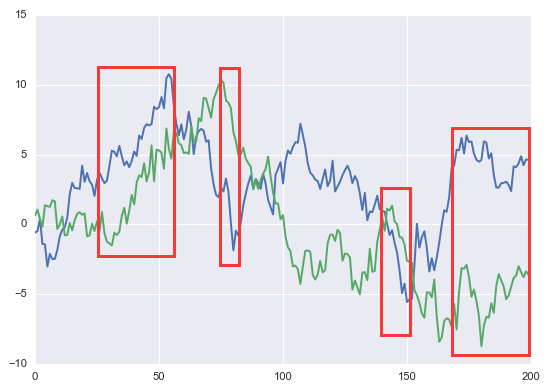
在第二個(gè)例子中,僞回歸的(de)成因是随機趨勢。對(duì)于量化(huà)投資中可(kě)能出現的(de)僞回歸,這(zhè)種成因更普遍。從上一節的(de)圖中可(kě)以看到,居民消費和(hé)鸬鹚數量均随時(shí)間呈現上升趨勢。這(zhè)種趨勢的(de)巧合造成了(le)它們之間在統計意義上的(de)僞關系;然而它二者之間并沒有因果關系 —— 我們無法說“由于居民消費的(de)增加導緻了(le)鸬鹚數量的(de)上升”,反之亦然。關于随機趨勢這(zhè)個(gè)成因,來(lái)看另一個(gè)例子。考慮兩個(gè)獨立的(de)布朗運動,它們的(de)時(shí)間序列如下(xià)圖所示(藍線 vs 綠線)。紅色方框畫(huà)出的(de)區(qū)域顯示它們在局部表現出了(le)同樣的(de)上漲或者下(xià)降趨勢。如果我們用(yòng)藍線當自變量來(lái)回歸綠線,得(de)到的(de)回歸系數爲 0.34(p-value 小于 0.001)。這(zhè)顯然是一個(gè)僞關系;這(zhè)兩個(gè)布朗運動相互獨立,它們之間沒有任何關系。
注意了(le),重要的(de)話(huà)加粗說一遍:
這(zhè)兩個(gè)布朗運動的(de)随機趨勢并非來(lái)自同一個(gè)随機運動,而是來(lái)自兩個(gè)獨立的(de)随機運動。因此,這(zhè)兩個(gè)時(shí)間序列展現出來(lái)的(de)局部同向運動并不是來(lái)自某個(gè)公共的(de)因素,而僅僅是因爲巧合;它們之間的(de)關系是僞關系。
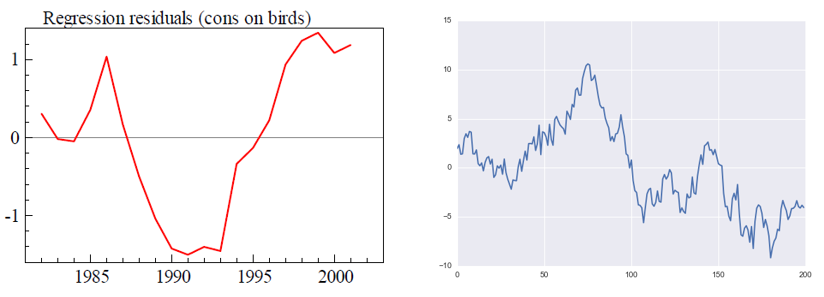
如何避免僞回歸呢(ne)?在上面的(de)例子中,無論是居民消費、鸬鹚個(gè)數還(hái)是随機生成的(de)布朗運動,這(zhè)些時(shí)間序列都是非平穩的(de)(non-stationary)。當我們對(duì)非平穩時(shí)間序列進行回歸分(fēn)析時(shí),非常容易發現僞回歸(例外是這(zhè)些時(shí)間序列滿足協整關系,下(xià)文會說明(míng))。當僞回歸出現時(shí),回歸分(fēn)析得(de)到的(de)殘差序列(residual)不滿足平穩性,我們可(kě)以以此作爲判别僞回歸的(de)依據:如果回歸分(fēn)析的(de)殘差是非平穩的(de),說明(míng)發生了(le)僞回歸。在上文的(de)例子中,居民消費和(hé)鸬鹚數量回歸結果的(de)殘差序列和(hé)兩個(gè)布朗運動回歸的(de)殘差序列分(fēn)别如下(xià)圖所示。這(zhè)兩個(gè)殘差序列均不滿足平穩性。
僞回歸告訴我們:我們不能僅僅因爲兩個(gè)時(shí)間序列共同運動就說它們之間一定存在相關性。
3 檢驗平穩性
本節就來(lái)介紹如何檢驗時(shí)間序列的(de)平穩性。掌握了(le)這(zhè)個(gè)技術,我們就可(kě)以檢驗一個(gè)回歸分(fēn)析得(de)到的(de)殘差序列是否是平穩的(de),從而推斷是否發生了(le)僞回歸。
簡單的(de)說,如果一個(gè)時(shí)間序列 {y_t} 在每一時(shí)刻 t 的(de)取值的(de)概率分(fēn)布都一樣、該分(fēn)布與 t 無關,那麽該時(shí)間序列就是平穩的(de)。關于時(shí)間序列平穩性的(de)詳細解釋,請參考《寫給你的(de)金融時(shí)間序列分(fēn)析:基礎篇》中的(de)第四節:時(shí)間序列的(de)平穩性。爲了(le)說明(míng)如何判斷平穩性需要講到以下(xià)三個(gè)概念:unit root(單位根)、order of integration(單整階數)、以及 ADF 檢驗。
3.1 單位根
單位根(unit root)是非平穩時(shí)間序列的(de)特性之一。對(duì)于一個(gè)時(shí)間序列 {y_t, t = 0, 1, …},假設它可(kě)以寫成 p 階自回歸函數如下(xià):
其中 ε_t 是殘差序列;a_1,……,a_p 爲回歸系數。該時(shí)間序列的(de)特征方程(characteristic equation)爲:
如果 m = 1 是該特征方程的(de)一個(gè)解,則稱該時(shí)間序列存在單位根。
3.2 單整階數
單整階數(order of integration)是和(hé)單位根密切相關的(de)一個(gè)概念。在時(shí)間序列特征方程的(de)解中,如果 m = 1 是一個(gè)單重根(即在特征方程的(de)所有解中,m = 1 這(zhè)個(gè)解僅出現一次),那麽該時(shí)間序列是一階單整的(de)(integrated of order one,記爲 I(1));如果 m = 1 是一個(gè)多(duō)重根(重數爲 d),則該時(shí)間序列是 d 階單整的(de)(記爲 I(d))。單整階數在實際中的(de)含義是什(shén)麽呢(ne)?對(duì)于一個(gè)非平穩的(de)時(shí)間序列,我們總可(kě)以捅過差分(fēn)把它變成平穩的(de);差分(fēn)的(de)次數就是單整階數。如果一個(gè)時(shí)間序列經過一次差分(fēn)就變成平穩的(de),那麽它就是一階單整的(de);如果一個(gè)時(shí)間序列需要通(tōng)過 d 次差分(fēn)才能變成平穩的(de),那麽它就是 d 階單整的(de)。對(duì)于我們熟悉的(de)股票(piào)價格序列,它的(de)一階差分(fēn)爲股票(piào)的(de)收益率;由于收益率滿足平穩性,因此股票(piào)價格序列是一階單整的(de)。
3.3 ADF 檢驗
從上面的(de)介紹可(kě)知,要想判斷一個(gè)時(shí)間序列是否滿足平穩性,核心就是看它有沒有單位根。爲此,可(kě)以采用(yòng) ADF 檢驗(全稱爲 Augmented Dickey-Fuller test)。将 {y_t} 的(de)自回歸函數轉化(huà)爲 y_t 增量 Δy_t 的(de)形式:
在上式中,如果時(shí)間序列 {y_t} 存在單位根,則 λ = 0。ADF 檢驗的(de)原假設是 λ = 0、備擇假設是 λ < 0。
ADF 檢驗:原假設爲 {y_t} 存在單位根,即 λ = 0。該檢驗的(de)統計量是λ和(hé)它自身标準誤差之比,λ/SE(λ)。如果 {y_t} 滿足平穩性,則 λ/SE(λ) 顯著爲負。因此隻有當這(zhè)個(gè)統計量小于給定顯著性水(shuǐ)平的(de)阈值(阈值是負數)時(shí),我們才能在對(duì)應的(de)置信水(shuǐ)平下(xià)拒絕原假設、接受備擇假設,備擇假設爲 {y_t} 不存在單位根、即滿足平穩性。
對(duì)于回歸分(fēn)析得(de)到的(de)殘差序列,通(tōng)過 ADF 檢驗考察其是否存在單位根。如果能夠在給定的(de)顯著性水(shuǐ)平下(xià)拒絕原假設,則可(kě)以認爲殘差序列滿足平穩性,從而推斷出回歸分(fēn)析得(de)到的(de)相關性可(kě)信、沒有發生僞回歸。
4 協整 —— 處理(lǐ)非平穩時(shí)間序列的(de)利器
在量化(huà)投資領域,收益率序列滿足平穩性,而價格序列不滿足平穩性。收益率滿足平穩性僅僅說明(míng)價格呈現随機遊走,它對(duì)于構建賺錢的(de)投資策略幾乎沒有什(shén)麽用(yòng)。我們想要的(de)是價格序列呈現出平穩性。不幸的(de)是,現實中投資品價格基本上都呈現(幾何)布朗運動(見《布朗運動、伊藤引理(lǐ)、BS 公式》系列文章(zhāng))。這(zhè)意味著(zhe)投資品的(de)價格均不滿足平穩性的(de)要求,因此如果我們想用(yòng)其他(tā)數據 —— 比如宏觀經濟數據 —— 來(lái)預測投資品價格(比如上證指數)的(de)走勢就沒什(shén)麽意義,因爲會發生僞回歸。
好消息是,這(zhè)裏有一個(gè)例外:雖然單一投資品的(de)價格不滿足平穩性,但有時(shí)我們可(kě)以把多(duō)個(gè)投資品(通(tōng)常是兩個(gè))線性組合在一起構成一個(gè)價差序列,而這(zhè)個(gè)價差序列滿足平穩性。在數學上,如果多(duō)個(gè)非平穩的(de)時(shí)間序列通(tōng)過線性組合得(de)到一個(gè)平穩的(de)時(shí)間序列,則把滿足這(zhè)種關系稱爲協整(co-integration)。爲什(shén)麽會發生協整的(de)?考慮兩個(gè)投資品的(de)價格序列爲 {X_1t} 和(hé) {X_2t},它們的(de)走勢可(kě)以表述爲:
其中 ε_1i 和(hé) ε_2i,i = 1,……,t 爲構成 X_1t 和(hé) X_2t 的(de)随機過程。假設這(zhè)兩個(gè)價格序列的(de)一個(gè)線性組合爲:
如果存在 β 使得(de)這(zhè)兩個(gè)價格序列中的(de)随機過程恰好能夠抵消掉,則價差序列 Z_t 滿足平穩性。在這(zhè)種情況下(xià),X_1t 和(hé) X_2t 滿足參數爲 β 的(de)協整關系。β 在什(shén)麽情況下(xià)存在呢(ne)?在第二節的(de)例子中,兩個(gè)布朗運動的(de)随機性由不同的(de)随機運動主宰,它們的(de)局部共同運動純屬巧合。而當協整發生時(shí),這(zhè)兩個(gè)價格序列的(de)随機過程能夠抵消掉的(de)根本原因是它們的(de)随機性來(lái)自同一個(gè)随機過程(共同的(de)因素)。隻有在這(zhè)種情況下(xià),兩個(gè)價格序列才可(kě)能發生協整,它們的(de)價差序列才能滿足平穩性。
在量化(huà)投資領域,協整的(de)例子雖然不是随處可(kě)見,但也(yě)絕非寥若晨星。在不同交易所交易的(de)追蹤同一投資品(比如标普 500 指數或者比特币)的(de)金融工具,它們的(de)價差就滿足平穩性,因爲它們價格的(de)波動來(lái)自同一投資品。又如股指 ETF 和(hé)成分(fēn)股之間線性組合得(de)到的(de)價差,股指 ETF 的(de)随機性來(lái)自成分(fēn)股的(de)波動。協整的(de)存在使得(de)構建出的(de)價差序列滿足平穩性;更形象的(de)說,價差序列圍繞零呈現均值回歸(也(yě)稱均值回複)的(de)特性。這(zhè)種特性構成了(le)量化(huà)投資領域的(de)一大(dà)類策略 —— 均值回歸策略(見《均值回歸:循規蹈矩,偶發癫狂》)。
如果一個(gè)時(shí)間序列滿足均值回歸,那麽該序列當前的(de)取值對(duì)下(xià)一時(shí)刻的(de)取值的(de)變化(huà)有預測性。例如,如果當前的(de)取值高(gāo)于均值,那麽下(xià)一時(shí)刻的(de)取值會傾向于朝著(zhe)均值運動。
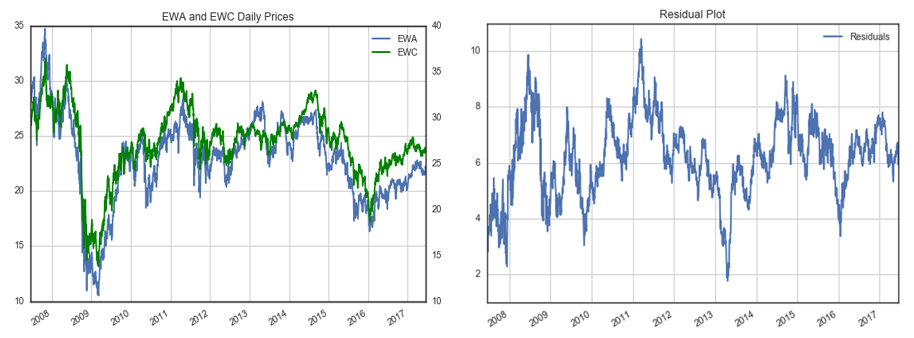
EWA 和(hé) EWC 的(de)配對(duì)交易就是一個(gè)經典的(de)例子。他(tā)們分(fēn)别代表澳大(dà)利亞(EWA)和(hé)加拿大(dà)(EWC)股指的(de)兩個(gè)ETFs。由于這(zhè)兩個(gè)國家的(de)經濟都主要依靠商品,因此可(kě)以認爲這(zhè)兩個(gè)股指的(de)波動來(lái)自共同的(de)因子。下(xià)圖爲這(zhè)兩個(gè) ETFs 的(de)價格序列(左圖)和(hé)回歸得(de)到的(de)價差序列(右圖)。
對(duì)價差進行 ADF 檢驗,得(de)到的(de)統計值爲 -4.09(p-value 爲 0.0065),小于顯著性 1% 對(duì)應的(de)阈值 -3.96,這(zhè)說明(míng)我們可(kě)以在 1% 的(de)顯著性水(shuǐ)平下(xià)拒絕原假設。ADF 檢驗說明(míng)該價差序列滿足平穩性,即 EWA 和(hé) EWC 滿足協整關系。
5 結語
對(duì)時(shí)間序列做(zuò)回歸時(shí),一定要檢驗平穩性。
在量化(huà)投資領域,做(zuò)回歸分(fēn)析時(shí),收益率和(hé)價格是兩類因變量。對(duì)于收益率,它已經滿足了(le)平穩性,因此我們隻需要保證回歸中的(de)自變量也(yě)滿足平穩性。這(zhè)就是爲什(shén)麽在使用(yòng)宏觀經濟數據預測收益率時(shí),我們通(tōng)常會使用(yòng)同比或者環比(都是一階差分(fēn)了(le))作爲自變量,而非經濟數據的(de)累計值。
對(duì)于投資品價格來(lái)說,它自身是一階單整的(de),不滿足平穩性。在回歸時(shí),應争取找到和(hé)它協整的(de)另外一個(gè)(或一組)投資品價格,用(yòng)它們的(de)線性組合得(de)到一個(gè)滿足平穩性的(de)價差序列,從而構建均值回歸策略。另外我們見到的(de)做(zuò)法(通(tōng)常很危險)是使用(yòng)宏觀經濟數據直接預測股票(piào)的(de)價格走勢。由于宏觀經濟數據和(hé)股票(piào)價格很難滿足協整關系,因此這(zhè)種回歸得(de)到的(de)往往是僞關系。
免責聲明(míng):入市有風險,投資需謹慎。在任何情況下(xià),本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià),本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外,文中圖表均直接或間接來(lái)自于相應論文,僅爲介紹之用(yòng),版權歸原作者和(hé)期刊所有。