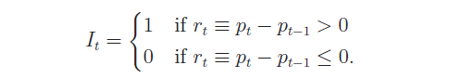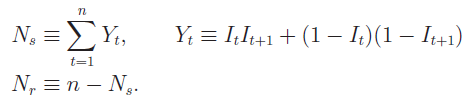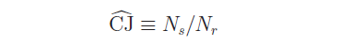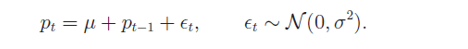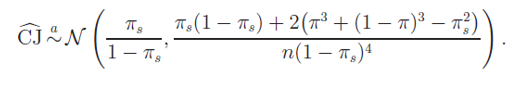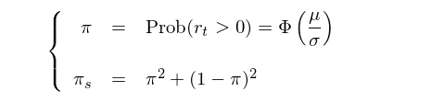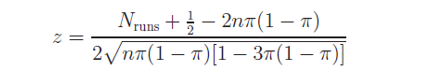收益率到底能不能預測（模型篇）？

作者：石川

摘要：“不要把時(shí)間序列中的(de)長(cháng)期漂移率項當成可(kě)預測性。”資産的(de)收益率可(kě)預測嗎？本文介紹檢驗時(shí)間序列随機性的(de)統計模型。

1 引言

不要把時(shí)間序列中的(de)長(cháng)期漂移率項當成可(kě)預測性。

這(zhè)是我近期看到的(de)頗受啓發的(de)一句話(huà)，它出自經濟計量學的(de)一本經典著作 Campbell et al. (1996)。在量化(huà)投資領域，人(rén)們較勁腦(nǎo)汁兒(ér)想要分(fēn)析、預測收益率這(zhè)個(gè)時(shí)間序列。從時(shí)間序列分(fēn)析到各種機器學習(xí)算(suàn)法，越來(lái)越複雜(zá)的(de)非線性模型都被拿來(lái)，對(duì)著(zhe)收益率序列就是一通(tōng)比劃，就是爲了(le)提高(gāo)對(duì)未來(lái)收益率預測的(de)準确性。

但是，可(kě)能人(rén)們都忽視了(le)一個(gè)核心的(de)問題：收益率到底可(kě)預測嗎？學術界和(hé)業界比較主流的(de)看法是，資産的(de)價格可(kě)以由随機遊走（random walk）過程來(lái)描述，這(zhè)對(duì)應的(de)是收益率無法預測。當然，如果價格是純粹的(de)随機遊走，那我們也(yě)不需要開發各種複雜(zá)的(de)數學模型了(le)，就每天扔硬币、猜漲跌就行了(le)。但是，這(zhè)不妨礙随機遊走成爲研究價格和(hé)收益率序列的(de)一個(gè)很好的(de)出發點。

談及随機遊走，人(rén)們第一個(gè)想到的(de)大(dà)概是布朗運動（見《寫給你的(de)金融時(shí)間序列分(fēn)析：初級篇》或《布朗運動、伊藤引理(lǐ)、BS 公式（前篇）》）。由于要求不重疊但等長(cháng)的(de)時(shí)間區(qū)間内的(de)過程增量（對(duì)數價格的(de)增量就是對(duì)數收益率）符合 IID 分(fēn)布（獨立且同分(fēn)布），布朗運動這(zhè)個(gè)版本的(de)随機遊走的(de)局限性非常強。因此在這(zhè)個(gè)版本的(de)基礎上，人(rén)們又提出了(le)另外兩個(gè)版本。算(suàn)上布朗運動，一共有三個(gè)版本，它們的(de)定義如下(xià)：

模型二在模型一的(de)基礎上，放松了(le)同分(fēn)布這(zhè)個(gè)限制；而模型三更是僅假設不同的(de)收益率之間滿足一階（線性）的(de)獨立性，而允許收益率在高(gāo)階上非獨立。我們經常觀察到資産收益率的(de)波動率聚類，這(zhè)說明(míng)收益率的(de)二階就不是獨立的(de)，因此模型三似乎更符合現實。

雖然現實中收益率很難滿足模型一的(de)假設，但隻有先對(duì)它有個(gè)正确的(de)理(lǐ)解才能更好的(de)搞清楚後續的(de)複雜(zá)模型。爲此，我們用(yòng)兩期文章(zhāng)來(lái)介紹相關内容。本篇（模型篇）介紹兩種檢驗方法以判斷一個(gè)時(shí)間序列是否滿足模型一。下(xià)篇（實證篇）使用(yòng)這(zhè)兩個(gè)方法對(duì)A股幾大(dà)股指的(de)對(duì)數收益率序列進行實證檢驗，并說明(míng)實證結果對(duì)于構建量化(huà)策略有何種借鑒意義。

這(zhè)兩種檢驗分(fēn)别爲順序和(hé)反轉檢驗以及遊程檢驗。它們都是非參數化(huà)檢驗。

2 順序和(hé)反轉檢驗

爲了(le)将對(duì)檢驗方法的(de)介紹和(hé)研究對(duì)象結合起來(lái)，假設我們考察的(de)是資産的(de)對(duì)數價格序列的(de)随機性。因此，它的(de)增量就是對(duì)數收益率。我們假設對(duì)數收益率的(de)分(fēn)布是對(duì)稱的(de)。第一種檢驗對(duì)數收益率是否爲 IID 的(de)方法是順序和(hé)反轉檢驗（sequences and reversals test），由Cowles and Jones (1937) 提出。對(duì)一個(gè)對(duì)數收益率，首先對(duì)其按如下(xià)轉換變成 0、1 序列：

其中 r_t ~ IID(0, σ^2) 和(hé) p_t 分(fēn)别爲某資産在 t 時(shí)刻的(de)對(duì)數收益率和(hé)對(duì)數價格。經過上述變換後，一個(gè)收益率序列就轉化(huà)爲一組由 0 和(hé) 1 組成的(de)序列，例如 1001110101011000011010。在這(zhè)樣一個(gè)序列中，任意相鄰的(de)兩個(gè)數如果同爲 0 或者同爲 1，則稱它們爲一個(gè)順序（sequence）；反之，如果任意相鄰的(de)兩個(gè)數爲 0 和(hé) 1、或者 1 和(hé) 0，則稱它們爲一個(gè)反轉（reversals）。根據這(zhè)個(gè)定義，我們可(kě)以在上面那個(gè)序列中用(yòng)紅色和(hé)綠色标出一些順序和(hé)反轉的(de)例子：1001110101011000011010。（注意，在前面我們僅僅标出一些示例。在實際計算(suàn)時(shí)，應該逐一考慮相鄰的(de)每對(duì)數是一個(gè)順序還(hái)是一個(gè)反轉。例如在 010 這(zhè)三個(gè)數中，就有 01 和(hé) 10 兩個(gè)反轉對(duì)兒(ér)、沒有順序對(duì)兒(ér)。）

在數學上，上述定義可(kě)以轉化(huà)爲如下(xià)簡單的(de)數學公式，通(tōng)過它們可(kě)以計算(suàn)出一個(gè)長(cháng)度爲 n 的(de)時(shí)間序列中，順序和(hé)反轉各自的(de)總個(gè)數：

其中 N_s 是順序對(duì)兒(ér)的(de)個(gè)數，N_r 是反轉對(duì)兒(ér)的(de)個(gè)數。有了(le) N_s 和(hé) N_r 之後，就可(kě)以定義待檢驗的(de)變量了(le)。爲了(le)向發明(míng)者緻敬，稱這(zhè)個(gè)檢驗量爲 CJ 統計量，那是 N_s 和(hé) N_r 的(de)比值：

先來(lái)考慮最簡單的(de)情況，即對(duì)數收益率沒有長(cháng)期漂移率項（即長(cháng)期均值爲 0）。這(zhè)當然不符合大(dà)多(duō)數實際情況，因爲它意味著(zhe)長(cháng)期來(lái)看買入和(hé)持有某種投資品是不掙錢的(de)（在商品期貨市場(chǎng)基本符合，但對(duì)于股市和(hé)債市，這(zhè)個(gè)假設很難成立）。在這(zhè)種情況下(xià)，如果收益率序列滿足 IID，則我們可(kě)以預期漲、跌出現的(de)次數也(yě)應該基本一樣，因此這(zhè)個(gè)序列中的(de)順序和(hé)反轉對(duì)兒(ér)數也(yě)應該基本一樣。因此，如果假設漂移率項爲零，則随著(zhe)序列個(gè)數 n 的(de)增大(dà)，CJ 統計量應該逐漸逼近 1。

然而，一旦考慮了(le)漂移率項，一切就變了(le)。我們不能再假設 CJ 統計量的(de)極限值爲 1。無論是一個(gè)正的(de)漂移率（意味著(zhe)長(cháng)期來(lái)看持有該資産是能掙錢的(de)）還(hái)是一個(gè)負的(de)漂移率（意味著(zhe)長(cháng)期來(lái)看持有該資産是注定虧損的(de)），這(zhè)個(gè)非零的(de)漂移率都将使收益率序列中順序對(duì)兒(ér)的(de)個(gè)數多(duō)餘反轉對(duì)兒(ér)的(de)個(gè)數，即 CJ 應該大(dà)于 1。爲了(le)量化(huà)非零漂移量對(duì) CJ 統計量的(de)影(yǐng)響，我們需要已知增量的(de)具體分(fēn)布，爲此選擇正态分(fēn)布。在考慮漂移率的(de)情況下(xià)，對(duì)數價格的(de)随機過程可(kě)描述爲：

其中 μ 是非零的(de)漂移率。由上述定義可(kě)知，對(duì)數收益率爲 r_t ~ N(μ, σ^2)。在這(zhè)種情況下(xià)，經過必要的(de)數學推導可(kě)以證明(míng) CJ 統計量應近似的(de)滿足如下(xià)正态分(fēn)布：

其中

因此，實際的(de)檢驗可(kě)依如下(xià)步驟進行：

3 遊程檢驗

第二個(gè)可(kě)用(yòng)于 IID 的(de)檢驗稱爲 runs test（遊程檢驗，也(yě)譯作連貫檢驗），由 Mood (1940) 提出。在這(zhè)個(gè)檢驗中，我們同樣先将對(duì)數收益率序列轉換成由 0 和(hé) 1 構成的(de)序列（0 代表負收益、1 代表正收益）。在這(zhè)個(gè)新的(de)序列中，由連續的(de)“0”或者連續的(de)“1”構成的(de)子序列稱爲一個(gè)“run”。比如，在 1001110100 這(zhè)個(gè)序列中，連續的(de)“1”構成的(de) runs 有 3 個(gè)（長(cháng)度分(fēn)别爲 1，3 和(hé) 1），連續的(de)“0”構成的(de) runs 同樣爲 3 個(gè)（長(cháng)度分(fēn)别爲 2，1 和(hé) 2）。作爲對(duì)比，在 0000011111 這(zhè)個(gè)序列中，連續的(de)“0”和(hé)“1”各自僅僅構成 1 個(gè) run。

如果一個(gè)時(shí)間序列的(de)增量滿足 IID 且沒有非零漂移率，那麽我們可(kě)以預期它的(de)“熵最大(dà)”，即 0 和(hé) 1 雜(zá)亂的(de)随機出現、表現出最大(dà)的(de)随機性。在這(zhè)種情況下(xià)，對(duì)于一個(gè)長(cháng)度爲 n 的(de)序列，它的(de)期望 runs 個(gè)數等于 (n+1)/2。比如一個(gè)由 0 和(hé) 1 構成的(de)長(cháng)度爲 1000 的(de)時(shí)間序列，如果它是純随機的(de)，那麽“0”和(hé)“1”構成的(de) runs 的(de)總個(gè)數的(de)期望爲 500.5。顯然，在上面的(de)兩個(gè)例子中，那兩個(gè)序列都各有 10 個(gè)數，但是第一個(gè)序列的(de) runs 個(gè)數爲 6 而第二個(gè)序列的(de) runs 個(gè)數僅僅爲 2；顯然第二個(gè)序列（0000011111）更不具備随機性（它看上去也(yě)确實更有規律）。

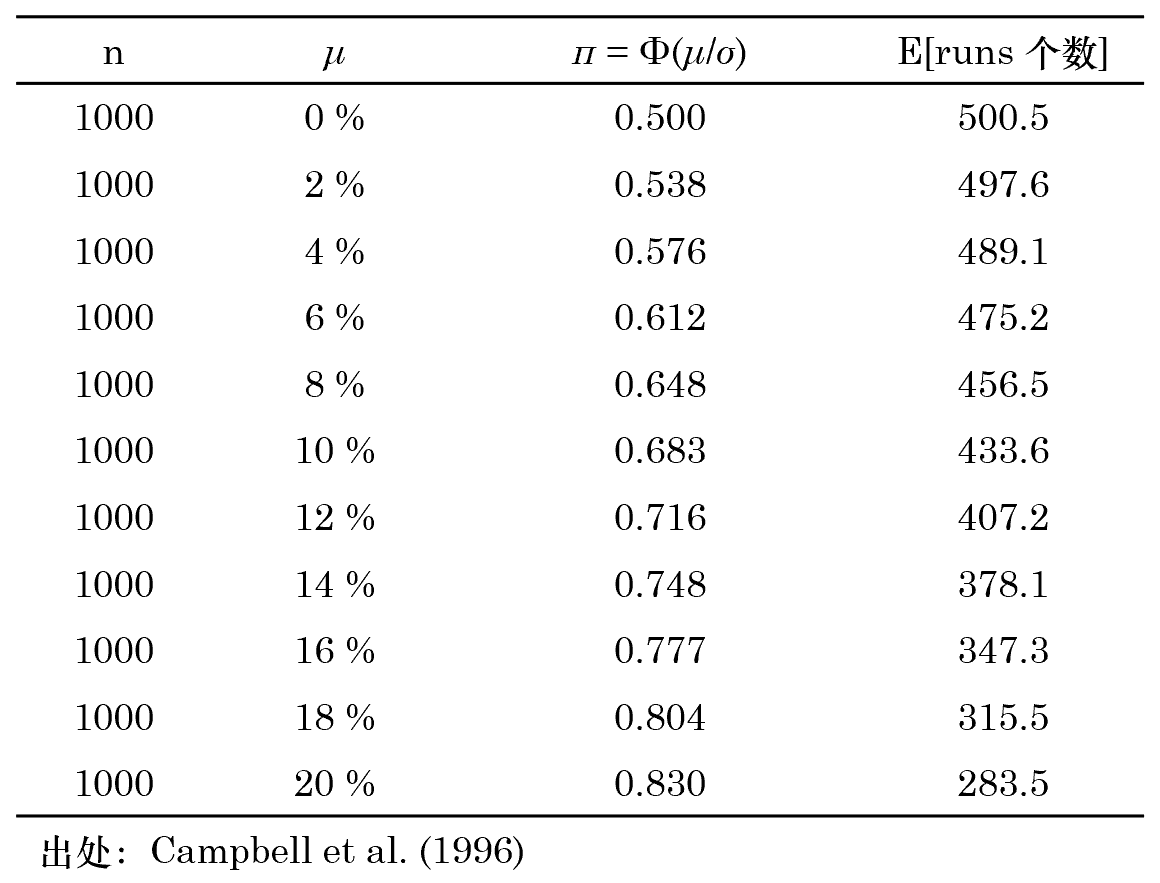
和(hé)前一種方法一樣，我們需要警惕非零漂移率對(duì) runs 個(gè)數的(de)影(yǐng)響。由于它的(de)存在，我們不能僅憑 runs 的(de)個(gè)數大(dà)大(dà)偏離 (n+1)/2 就說這(zhè)個(gè)序列不具備随機性。這(zhè)是因爲非零漂移率會減少 runs 的(de)個(gè)數。爲了(le)定量分(fēn)析非零漂移率的(de)影(yǐng)響，讓我們再次假設對(duì)數收益率 r_t 滿足 N(μ, σ^2)。在這(zhè)個(gè)假設下(xià)，下(xià)表給出了(le)當 n = 1000，σ = 21%時(shí)，不同的(de)漂移率 μ 對(duì)應的(de) runs 個(gè)數的(de)期望。不難看出，runs 個(gè)數的(de)期望随 μ 遞減。

爲了(le)使用(yòng) runs test 檢驗對(duì)數收益率的(de)随機性，構建如下(xià)統計量：

其中 N_runs 是由“0”和(hé)“1”構成的(de) runs 數量的(de)總和(hé)（每個(gè) run 的(de)長(cháng)度在這(zhè)個(gè)檢驗中不重要），n 爲時(shí)間序列長(cháng)度，π = Φ(μ/σ)。數學上可(kě)證 z 在極限情況下(xià)近似的(de)符合标準正态分(fēn)布。因此，實際的(de)檢驗可(kě)依如下(xià)步驟進行：

4 一個(gè)例子

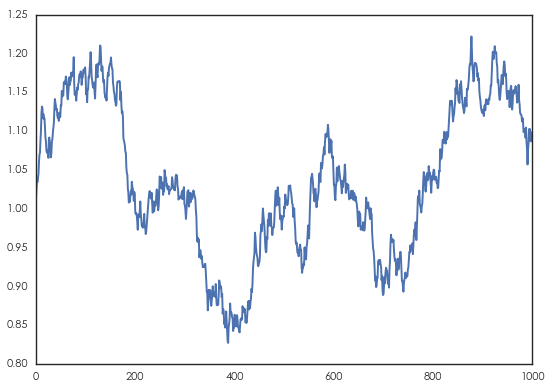
下(xià)面使用(yòng)一個(gè)假想的(de)例子來(lái)考察上文介紹的(de)兩個(gè)檢驗方法。爲此，我們使用(yòng)标準正态分(fēn)布産生一個(gè)随機遊走過程如下(xià)，序列的(de)長(cháng)度爲 1000。

盡管這(zhè)是一個(gè)标準的(de)随機遊走，但局部随機趨勢（local stochastic trend）的(de)存在會給我們造成一種假象，即認爲它是有趨勢的(de)。使用(yòng)本文介紹的(de)兩種檢驗方法考察這(zhè)個(gè)時(shí)間序列的(de)随機性，得(de)到如下(xià)結果：

雖然該序列在局部存在趨勢，但在整個(gè)時(shí)間尺度上看，它滿足随機遊走。（這(zhè)當然也(yě)是必然的(de)結果，因爲這(zhè)個(gè)序列就是用(yòng) IID 的(de)标準正态分(fēn)布增量産生的(de)。）但我們想通(tōng)過它說明(míng)的(de)問題是，哪怕是一個(gè)随機性很高(gāo)的(de)時(shí)間序列在其局部也(yě)會因爲随機趨勢給我們造成一種錯覺 —— 它的(de)随機性很弱、是可(kě)以預測的(de)。

根據這(zhè)個(gè)錯覺來(lái)構建策略是非常危險的(de)。這(zhè)是因爲任何資産的(de)實際價格走勢都是某個(gè)未知分(fēn)布的(de)一個(gè)realization（實現）而已。如果抓住這(zhè)個(gè)錯覺、認爲該資産的(de)價格走勢有一定的(de)預測性（即收益率有預測性），并針對(duì)它開發了(le)一個(gè)策略，我們根本無法預期該策略在樣本外有同樣的(de)表現。

由于僅有一個(gè)實現（過去這(zhè)段時(shí)間的(de)價格走勢隻發生一遍），我們無法在統計上正确的(de)評價該策略的(de)參數對(duì)這(zhè)個(gè)未知收益率分(fēn)布是否有效，正如我們不知道在樣本外，随機趨勢有多(duō)大(dà)以及它什(shén)麽時(shí)候出現。策略在樣本外的(de)表現很有可(kě)能和(hé)其在樣本内的(de)表現大(dà)相徑庭。

當然，先不用(yòng)急著(zhe)“過度悲觀”，畢竟上面這(zhè)個(gè)例子中使用(yòng)的(de)時(shí)間序列就是一個(gè)随機遊走。在本系列的(de)下(xià)篇（實證篇）我們會使用(yòng)真實的(de)來(lái)自 A 股指數的(de)價格序列，分(fēn)析它們的(de)對(duì)數收益率是否存在非随機性，以及分(fēn)析結果對(duì)構建量化(huà)策略有哪些重要的(de)推論。

5 結語

作爲系列的(de)模型篇，本文介紹了(le)兩種檢驗時(shí)間序列随機性的(de)方法。在下(xià)篇中，我們将使用(yòng)這(zhè)些方法分(fēn)析 A 股的(de)股指（如滬深 300 指數）對(duì)數收益率的(de)随機性。爲了(le)和(hé)開篇的(de)那句引用(yòng)相呼應，不妨來(lái)個(gè)劇透。在大(dà)多(duō)數時(shí)間内，指數的(de)對(duì)數收益率均滿足 IID；隻有當明(míng)顯的(de)大(dà)牛、大(dà)熊市的(de)時(shí)候，才能觀察到統計上顯著的(de)非随機性。

無論是時(shí)間序列分(fēn)析還(hái)是複雜(zá)的(de)機器學習(xí)算(suàn)法，都是爲了(le)分(fēn)析收益率的(de)殘差項（即排除了(le)收益率中的(de)長(cháng)期漂移率、周期性等之後所剩餘的(de)部分(fēn)）是否存在預測性。如果殘差滿足非随機性，這(zhè)些複雜(zá)算(suàn)法自然大(dà)有可(kě)爲。但是不要忘記，在大(dà)牛、大(dà)熊市中，收益率的(de)漂移率項也(yě)顯著的(de)不爲零。那麽，在一個(gè)很強的(de)非零漂移率項面前，殘差中的(de)非随機性到底是“錦上添花”還(hái)是“畫(huà)蛇添足”呢(ne)（反正不是“雪(xuě)中送炭”）？下(xià)篇中将給出我們的(de)思考。

參考文獻

Campbell, J. Y., A. W. Lo, and C. MacKinlay (1996). The econometrics of financial markets. Princeton University Press.

Cowles, A. and H. E. Jones (1937). Some a posterior probabilities in stock market action. Econometrica 5, 280 – 294.

Mood, A. (1940). The distribution theory of runs. Annals of Mathematical Statistics 11, 367 – 392.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。