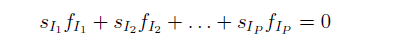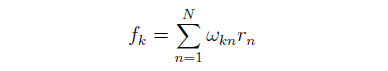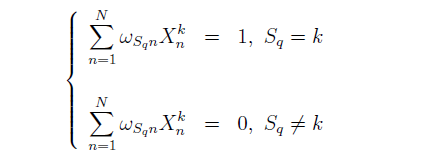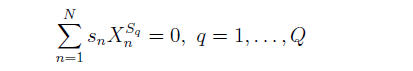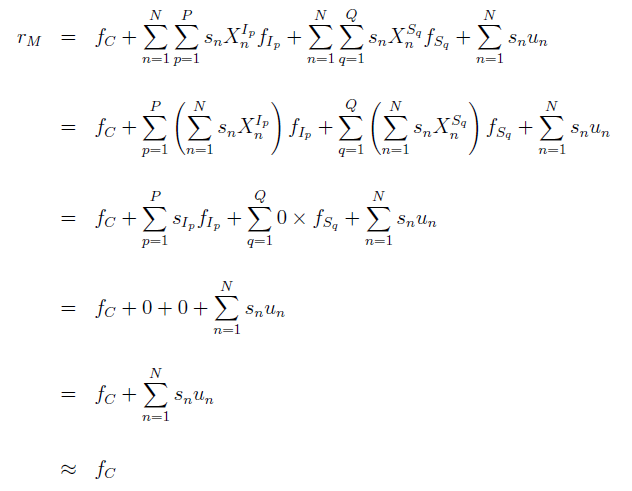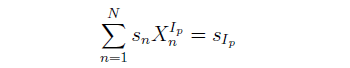正确理(lǐ)解 Barra 的(de)純因子模型

作者：石川

本文以 CNE5 模型爲例，解釋 Barra 的(de)純因子模型。純因子模型在風險歸因、因子評價等方面具備優勢。

1 引言

在（風險）多(duō)因子模型中，因子暴露（factor exposure）和(hé)因子收益率（factor return）是兩個(gè)核心的(de)概念。不清楚它們的(de)定義将影(yǐng)響對(duì)多(duō)因子模型的(de)理(lǐ)解。所謂因子，就是一個(gè)可(kě)以描述股票(piào)某方面特征的(de)因素，比如行業因子描述了(le)股票(piào)是否屬于這(zhè)個(gè)行業，P/E 因子描述股票(piào) Price-to-Earnings ratio。因子暴露就是股票(piào)在因子所代表的(de)特征上的(de)取值，比如一個(gè)股票(piào)的(de) P/E 爲 15.9，那麽它對(duì) P/E 因子的(de)因子暴露就是 15.9（實際使用(yòng)中，需要将這(zhè)個(gè)數值标準化(huà)）。對(duì)于一個(gè)給定的(de)因子，按照(zhào)某種權重組合所有股票(piào)便形成了(le)一個(gè)基于該因子構建的(de)投資組合，該投資組合的(de)收益率就被定義爲這(zhè)個(gè)因子的(de)收益率。

對(duì)于給定的(de)因子，如何構建因子投資組合呢(ne)？常見的(de)做(zuò)法是，将所有個(gè)股在該因子上的(de)因子暴露在截面上标準化(huà)；之後所有股票(piào)會按照(zhào)因子的(de)業務邏輯、根據因子暴露的(de)數值從好到壞排列；最後，假設做(zuò)多(duō)前 10% 或者 20% 的(de)股票(piào)，做(zuò)空後 10% 或者 20% 的(de)股票(piào)，以此來(lái)構建一個(gè)零額投資的(de)投資組合，它就是該因子的(de)投資組合。這(zhè)個(gè)做(zuò)法在業界非常流行，但它也(yě)存在兩個(gè)缺陷：

第一個(gè)問題造成在時(shí)間序列上評價一個(gè)因子的(de)作用(yòng)時(shí)，每期的(de)投資組合對(duì)該因子的(de)暴露程度都不一樣。舉個(gè)例子，假如相鄰兩個(gè)月(yuè)中，某因子的(de)投資組合對(duì)該因子的(de)暴露爲 1 和(hé) 2，而相應的(de)因子收益率爲 1% 和(hé) 2%。如果我們忽視了(le)因子暴露程度不同的(de)話(huà)，就會得(de)到本期因子收益率較前一期的(de)數值有所提高(gāo)的(de)錯誤結論。

第二個(gè)問題更爲嚴重。風險因子大(dà)多(duō)來(lái)源于股票(piào)的(de)基本面數據，很多(duō)因子之間存在一定的(de)線性相關性。爲了(le)正确的(de)評價一個(gè)風險因子是否有效以及在什(shén)麽程度上有效，必須保證圍繞該因子來(lái)構建的(de)投資組合可(kě)以最大(dà)程度的(de)剝離因子之間的(de)相關性。換句話(huà)說，針對(duì)某因子構建的(de)投資組合應該避免在其他(tā)因子上有任何暴露。

爲此，Barra（如今已被 MSCI 收購(gòu)了(le)）提出了(le)純因子模型（pure factor model），它能夠保證在截面上構建因子投資組合時(shí)，每個(gè)因子的(de)投資組合對(duì)目标因子有 1 個(gè)單位的(de)暴露，而對(duì)其他(tā)因子的(de)暴露爲 0*。 

純因子投資組合是爲了(le)正确量化(huà)因子的(de)收益和(hé)風險而從純數學的(de)角度構建的(de)。建立時(shí)沒有考慮任何可(kě)投資性的(de)要求，因此純因子投資組合的(de)可(kě)投資性非常低。它滿足對(duì)目标因子有 1 個(gè)單位的(de)暴露，對(duì)其他(tā)因子沒有暴露，因此可(kě)以正确的(de)衡量因子的(de)有效性。

看到這(zhè)裏也(yě)許有的(de)小夥伴會說“沒有可(kě)投資性那有什(shén)麽用(yòng)？”。正确的(de)解答(dá)是，Barra 的(de)風險因子模型的(de)核心是做(zuò)風險分(fēn)析。具體來(lái)說有兩個(gè)目的(de)：

爲了(le)上面兩個(gè)目标，構建因子的(de)投資組合時(shí)必須能夠正确計算(suàn)因子收益率，這(zhè)就是純因子組合的(de)價值所在。雖然純因子組合可(kě)投資性低，但它在風險管理(lǐ)和(hé)業績歸因中有著(zhe)非常重要的(de)作用(yòng)。今天我們就來(lái)簡單聊聊 Barra 的(de)純因子模型。行文的(de)重點将放在從定性層面理(lǐ)解這(zhè)個(gè)模型的(de)優點。

2 CNE5 模型

CNE5 是 Barra 的(de)最新一代面向中國股票(piào)市場(chǎng)的(de)多(duō)因子模型。該模型考慮了(le)一個(gè)國家因子、多(duō)個(gè)行業因子以及多(duō)個(gè)風格因子。假設市場(chǎng)中共有 N 支股票(piào)，P 個(gè)行業，以及 Q 個(gè)風格因子。在任意給定時(shí)間點，該模型使用(yòng)因子暴露和(hé)個(gè)股收益率構建截面回歸（cross-sectional regression）如下(xià)：

其中 r_n 是第 n 支股票(piào)的(de)收益率，r_f 是無風險收益率。X_n^{I_p} 是股票(piào) n 在行業 I_p 的(de)暴露，如果假設一個(gè)公司隻能屬于一個(gè)行業，那麽 X_n^{I_p} 的(de)取值爲 0（代表該股票(piào)不屬于這(zhè)個(gè)行業）或者 1（代表該股票(piào)屬于這(zhè)個(gè)行業）。X_n^{S_q} 是股票(piào) n 在風格因子 S_q 的(de)暴露，它的(de)取值經過了(le)某種标準化(huà)（标準化(huà)的(de)方法會在下(xià)文說明(míng)）。u_n 爲股票(piào) n 的(de)超額收益中無法被因子解釋的(de)部分(fēn)，因此也(yě)被稱爲該股票(piào)的(de)特質性性收益。f_C 爲國家因子的(de)因子收益率（所有股票(piào)在國家因子上的(de)暴露都是1）；f_{I_p} 爲行業 I_p 因子的(de)因子收益率；f_{S_q} 爲風格因子 S_q 的(de)因子收益率。

對(duì)于給定某一期截面數據（記爲 T 期），在截面回歸時(shí)，Barra 使用(yòng) T 期股票(piào)（超額）收益率對(duì) T - 1 期因子暴露回歸。在 USE4 模型中，因子收益率是日頻(pín)的(de)，因此截面回歸也(yě)應該是日頻(pín)的(de)。以下(xià)說明(míng)來(lái)自 Barra Risk Model Handbook。

... the previous steps have defined the exposures of each asset to the factors at the beginning of every period in the estimation window. The factor excess returns over the period are then obtained via a cross-sectional regression of asset excess returns on their associated factor exposures ...    

上式就是 CNE5 多(duō)因子模型。在這(zhè)個(gè)模型中，國家因子的(de)因子暴露和(hé) P 個(gè)行業的(de)因子暴露之間存在共線性。具體來(lái)說，國家因子的(de)因子暴露向量可(kě)以表達爲 P 個(gè)行業因子因子暴露向量的(de)線性組合。這(zhè)會造成上式的(de)解不唯一。爲此，對(duì)行業因子的(de)因子收益率作如下(xià)限制：

其中 s_{I_p} 是所有屬于行業 I_p 的(de)股票(piào)的(de)按流通(tōng)市值計算(suàn)出的(de)權重之和(hé)。通(tōng)過截面回歸，對(duì) CNE5 模型求解的(de)對(duì)象是每個(gè)因子的(de)投資組合中所有股票(piào)的(de)配比權重。對(duì)于因子 k 和(hé)股票(piào) n 來(lái)說，用(yòng)符号 ω_{kn} 來(lái)表示。一旦得(de)到所有的(de) ω_{kn}，便可(kě)通(tōng)過下(xià)式求出當期因子的(de)收益率 f_k:

對(duì) CNE5 模型求解其實是一個(gè)多(duō)因子回歸的(de)求解。把多(duō)個(gè)因子放在一起回歸同時(shí)求解就是爲了(le)考慮不同因子之間的(de)相關性。這(zhè)可(kě)以保證根據因子權重 ω_{kn} 來(lái)構建的(de)因子投資組合對(duì)于這(zhè)個(gè)模型所涉及的(de)所有因子都是純因子的(de)投資組合。對(duì)于任何一個(gè)風格因子 S_q，上述截面回歸保證了(le)它的(de)投資組合僅僅在這(zhè)個(gè)因子上有 1 個(gè)單位的(de)暴露，而在其他(tā)所有因子上均沒有任何暴露，即

對(duì)于國家因子和(hé)行業因子的(de)投資組合，“純因子”組合的(de)解釋略有不同，我們會在第 4 節中闡述。前面說到，在使用(yòng)截面回歸求解時(shí)，必須對(duì)風格因子的(de)因子暴露進行标準化(huà)（國家和(hé)行業因子的(de)因子暴露不需要标準化(huà)）。令 s_n 表示股票(piào) n 的(de)流通(tōng)市值權重。對(duì)風格因子的(de)因子暴露進行标準化(huà)的(de)初衷是這(zhè)樣的(de)：按照(zhào)股票(piào)的(de)流通(tōng)市值權重構建的(de)投資組合等同于整個(gè)市場(chǎng)，而市場(chǎng)對(duì)所有的(de)風格因子都應該是中性的(de)。因此，按流通(tōng)市值權重構建的(de)股票(piào)投資組合在所有風格因子上的(de)暴露必須是 0。這(zhè)意味著(zhe)經過标準化(huà)後的(de)風格因子暴露 X_n^{S_q} 必須滿足：

此外，我們還(hái)必須對(duì)風格因子的(de)因子暴露進行标準差的(de)标準化(huà)，即要求對(duì)每一個(gè)風格因子 S_q，X_n^{S_q} 的(de)标準差爲 1。這(zhè)樣便完成了(le)對(duì)風格因子的(de)因子暴露的(de)标準化(huà)。

3 國家因子

相比于早期的(de)中國股票(piào)因子模型，CNE5 中的(de)關鍵變化(huà)之一是加入了(le)國家因子。（類似的(de)，在針對(duì)美(měi)國市場(chǎng)的(de)最新模型 USE4 中，Barra 也(yě)加入了(le)這(zhè)一因子。）那麽，國家因子投資組合的(de)本質是什(shén)麽呢(ne)？國家因子投資組合的(de)實質是按流通(tōng)市值爲權重的(de)市場(chǎng)組合。有點繞？沒關系，一步一步來(lái)。對(duì)于國家因子，所有個(gè)股的(de)暴露都是 1，這(zhè)個(gè)組合的(de)收益率爲 f_C。而在市場(chǎng)組合中，個(gè)股是按流通(tōng)市值權重配置的(de)，我們用(yòng) r_M 表示市場(chǎng)組合的(de)收益。那麽，隻有當 f_C 近似的(de)等于 r_M 時(shí)，上面的(de)結論才成立。下(xià)面就來(lái)看看 f_C 和(hé) r_M 是否近似相等。

由前文所述，s_n 是股票(piào) n 的(de)流通(tōng)市值權重。将 {s_n}, n = 1, …, N 這(zhè)一組權重帶入到 CNE5 的(de)因子模型中可(kě)以得(de)到如下(xià)關系。其中左側就是市場(chǎng)收益 r_M，右側是使用(yòng)國家因子、行業因子、風格因子、以及個(gè)股特質性收益率對(duì) r_M 的(de)分(fēn)解。

上式中最後一項是所有股票(piào)特質性收益的(de)和(hé)，由于它的(de)值非常小（接近 0），因此在推導的(de)最後一步被忽略了(le)。推導中的(de)核心在于倒數第三步中的(de)中間兩項如何變爲 0。對(duì)于第一個(gè) 0，它用(yòng)到了(le)行業因子收益率按行業市值加權爲 0 以排除行業和(hé)國家因子之間的(de)共線性這(zhè)個(gè)約束條件。對(duì)于第二個(gè) 0，它是根據風格因子是使用(yòng)流通(tōng)市值權重來(lái)标準化(huà)這(zhè)個(gè)定義來(lái)的(de)。由此可(kě)見，在 CNE5 模型的(de)定義下(xià)，f_C 這(zhè)個(gè)國家因子收益率确實近似的(de)代表了(le)市場(chǎng)組合的(de)收益率，因此國家因子的(de)組合就（近似地）是市場(chǎng)組合。在新版多(duō)因子模型中增加這(zhè)一項是非常必要的(de)。事實上，在對(duì) CNE5 進行截面回歸求解後可(kě)以發現，國家因子的(de)投資組合中，個(gè)股 n 的(de)權重 ω_{Cn} 非常接近它的(de)流通(tōng)市值權重 s_n。

4 純因子投資組合的(de)性質

通(tōng)過上面的(de)介紹我們已經知道，Barra 的(de)截面回歸模型針對(duì)國家因子、行業因子以及風格因子分(fēn)别構建了(le)純因子投資組合。那麽，這(zhè)些組合有著(zhe)怎樣的(de)性質呢(ne)？

4.1 國家純因子投資組合

由 f_C ≈ r_M 可(kě)知，國家純因子投資組合就是近似的(de)市場(chǎng)組合，它是純多(duō)頭組合：

4.2 行業純因子投資組合

行業因子的(de)純因子投資組合是一個(gè)多(duō)空組合，它滿足以下(xià)特征：

4.3 風格純因子投資組合

風格因子的(de)純因子投資組合同樣是一個(gè)多(duō)空組合，它滿足下(xià)列特征：

暫時(shí)抛開純因子組合的(de)可(kě)投資性，上面的(de)結果對(duì)于因子投資有著(zhe)非常重要的(de)意義。它說明(míng)，如果我們從整體上看好市場(chǎng)，那麽隻需要持有國家因子的(de)純因子組合（即近似的(de)市場(chǎng)組合）；如果我們看好了(le)某些行業，那麽隻需要持有那些特定行業的(de)行業純因子組合，從而賺取行業相對(duì)于市場(chǎng)的(de)超額收益；如果我們看好了(le)某個(gè)風格因子（比如小市值、價值等），那麽隻需要持有這(zhè)些因子的(de)純因子組合，去賺取通(tōng)過暴露于這(zhè)些因子的(de)超額收益。

以上就是 Barra 這(zhè)個(gè)模型的(de)最大(dà)意義 —— 它可(kě)以針對(duì)我們喜歡的(de)因子（無論是市場(chǎng)、行業或是風格），構建出純粹的(de)僅僅針對(duì)于那些因子的(de)投資組合，從而捕捉這(zhè)些因子的(de)風險收益。

5 理(lǐ)解風險因子收益率

經過了(le)上一節的(de)解釋，我們更願意把因子收益理(lǐ)解爲一籃子股票(piào)（即圍繞該因子構建的(de)投資組合）的(de)共性收益（系統性風險溢價）。該投資組合如果賺錢，那麽靠的(de)是該投資組合在該風險因子上的(de)單位暴露，靠的(de)是該風險因子在時(shí)間維度上所帶來(lái)的(de)有效而穩定的(de)風險溢價。從風險暴露的(de)角度來(lái)說，所有股票(piào) —— 無論被做(zuò)多(duō)還(hái)是被做(zuò)空 —— 在該組合中的(de)貢獻都是“一樣的(de)”，都是必不可(kě)少的(de)。這(zhè)和(hé)精選個(gè)股（通(tōng)過深度研究或者靠其他(tā)歪門邪道）來(lái)賺取個(gè)股的(de)特質性收益 u_n 是完全不同的(de)，因爲純因子投資組合中股票(piào)的(de)特質性收益幾乎爲 0。

當然，在現實中，我們不得(de)不面對(duì)“可(kě)投資性”的(de)問題。當我們無法按照(zhào)純因子投資組合的(de)權重來(lái)實際構建投資組合（比如無法做(zuò)空一些股票(piào)）時(shí)，我們就面臨兩個(gè)問題：

以上兩點說明(míng)，在種種限制下(xià)，如果構建的(de)投資組合的(de)權重和(hé)純因子投資組合理(lǐ)論權重不一緻時(shí)，該投資組合便沒有有效的(de)暴露在該因子之下(xià)，也(yě)沒有對(duì)其他(tā)因子隔離。此外，該組合又引入了(le)無法忽略的(de)特質性收益的(de)風險。

美(měi)國的(de) AQR 基金寫過一篇文章(zhāng)來(lái)分(fēn)析巴菲特的(de)選股能力（Frazzini et al. 2013）。結果顯示，巴菲特選股的(de)收益率幾乎可(kě)以完全被 1 個(gè)市場(chǎng)因子和(hé) 5 個(gè)風格因子的(de)收益率來(lái)解釋。它說明(míng)巴菲特的(de)投資組合能賺錢是因爲它以一定的(de)權重有效的(de)暴露在了(le)這(zhè) 6 個(gè)因子之中，長(cháng)期穩定地賺取了(le)這(zhè) 6 個(gè)因子的(de)風險溢價。巴菲特有一個(gè)科學的(de)價值投資框架來(lái)保證它的(de)投資組合對(duì)最合理(lǐ)的(de)風險因子有著(zhe)最合理(lǐ)的(de)風險暴露，這(zhè)些風險因子的(de)風險溢價爲他(tā)帶來(lái)了(le)年複一年的(de)優秀收益。

6 不是所有的(de)風險因子都被定價

對(duì) CNE5 的(de)求解僅僅用(yòng)到了(le)給定時(shí)間（比如某月(yuè)或者某季度）的(de)股票(piào)截面數據。因此，得(de)到的(de)因子收益率僅僅反映在該時(shí)刻因子能取得(de)什(shén)麽樣的(de)收益。爲了(le)驗證一個(gè)風險因子是否可(kě)以有效的(de)帶來(lái)超額收益，我們必須在時(shí)序上對(duì)該因子的(de)收益率做(zuò)統計分(fēn)析。

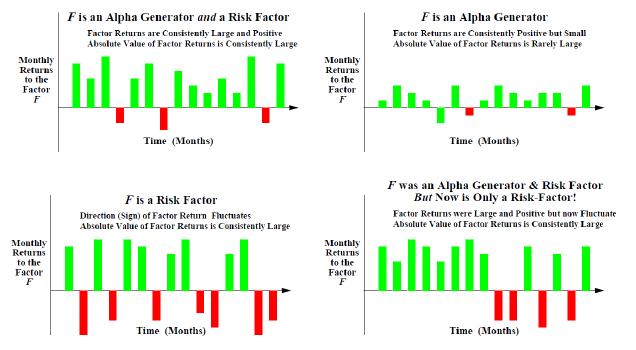
上圖展示了(le) 4 種典型的(de)因子收益率在時(shí)間維度上的(de)統計特征：

在評價一個(gè)風險因子時(shí)，應按照(zhào)正确的(de)方法得(de)到每個(gè)時(shí)間截面的(de)純因子投資組合，進而算(suàn)出每一期的(de)因子收益率。然後，通(tōng)過對(duì)因子收益率的(de)時(shí)間序列進行統計分(fēn)析，最終判定該因子能否在長(cháng)期穩定的(de)貢獻超額收益。同時(shí)，對(duì)因子收益率的(de)統計分(fēn)析也(yě)可(kě)以得(de)到因子收益率之間的(de)協方差矩陣，它是推導個(gè)股之間的(de)協方差矩陣的(de)必要條件之一。

參考文獻

Frazzini, A., D. Kabiller, and L. H. Pedersen (2013). Buffett's alpha. Working paper 19681, National Bureau of Economic Research.

Barra Risk Model Handbook (2007). MSCI.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。