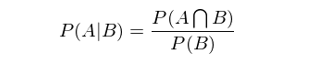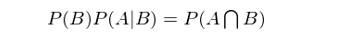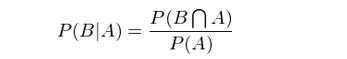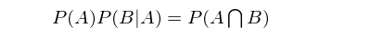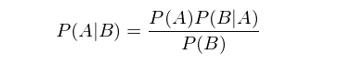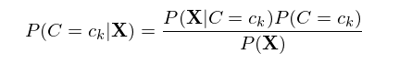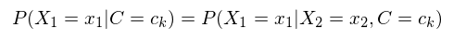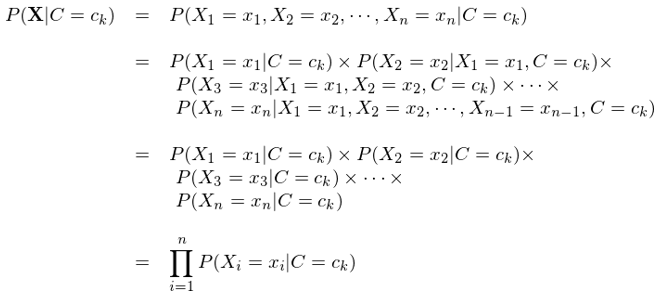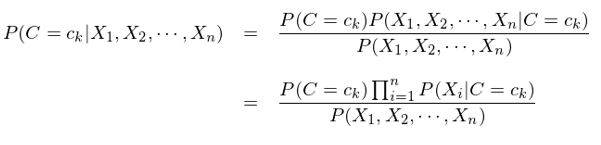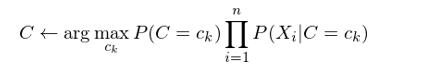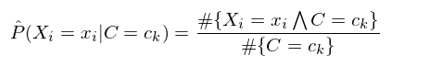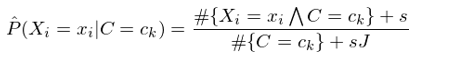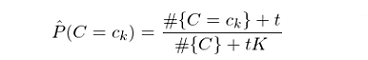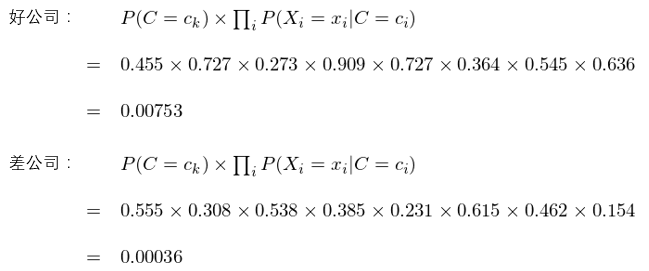樸素貝葉斯分(fēn)類器

作者：石川

摘要：樸素貝葉斯分(fēn)類器由于假設特征之間條件獨立，使用(yòng)起來(lái)非常簡單。它在實戰中的(de)效果往往非常優秀。

1 引言

有監督分(fēn)類是量化(huà)投資中常見的(de)情景之一。比如，我們希望根據上市公司财報中的(de)各種指标特征，區(qū)分(fēn)出優秀的(de)和(hé)差勁的(de)股票(piào)，這(zhè)就是一個(gè)分(fēn)類問題。在機器學習(xí)中，有監督分(fēn)類的(de)算(suàn)法有很多(duō)，比如 SVM、ANN 以及基于決策樹的(de) AdaBoost 和(hé)随機森林(lín)等。這(zhè)其中自然也(yě)少不了(le)今天的(de)主角樸素貝葉斯分(fēn)類器（Naïve Bayes classifiers）。它代表著(zhe)一類應用(yòng)貝葉斯定理(lǐ)的(de)分(fēn)類器的(de)總稱。樸素（naive）在這(zhè)裏有著(zhe)特殊的(de)含義、代表著(zhe)一個(gè)非常強的(de)假設（下(xià)文會解釋）。

樸素貝葉斯分(fēn)類器雖然簡單，但是用(yòng)處非常廣泛（尤其是在文本分(fēn)類方面）。在 IEEE 協會于 2006 年列出的(de)十大(dà)數據挖掘算(suàn)法中，樸素貝葉斯分(fēn)類器赫然在列（Wu et al. 2008）。捎帶一提，另外九個(gè)算(suàn)法是 C4.5、k-Means、SVM、Apriori、EM、PageRank、AdaBoost、kNN 和(hé) CART（那時(shí)候深度學習(xí)還(hái)沒有什(shén)麽發展）。

樸素貝葉斯分(fēn)類器以貝葉斯定理(lǐ)爲基礎。在《貝葉斯統計》一文中，我們曾介紹過貝葉斯定理(lǐ)。爲了(le)保證本文的(de)完整性，在下(xià)面首先回顧一下(xià)（熟悉貝葉斯定理(lǐ)的(de)朋友可(kě)以跳過第 2 節）。之後會闡釋“樸素”的(de)意義并介紹樸素貝葉斯分(fēn)類器。文章(zhāng)的(de)最後使用(yòng)一個(gè)例子說明(míng)如何使用(yòng)樸素貝葉斯分(fēn)類器選股。

2 貝葉斯定理(lǐ)

貝葉斯定理(lǐ)的(de)推導始于條件概率。條件概率可(kě)以定義爲：在事件 B 發生的(de)前提下(xià)，事件 A 發生的(de)概率。數學上用(yòng) P(A|B) 來(lái)表示該條件概率。條件概率 P(A|B) 的(de)數學定義爲：

這(zhè)個(gè)公式的(de)白話(huà)解釋爲：“當 B 發生前提下(xià) A 發生的(de)概率”等于“A 和(hé) B 同時(shí)發生的(de)概率”除以“B 發生的(de)概率”。生活中條件概率屢見不鮮。比如“在沒有趕上 8 點這(zhè)趟地鐵的(de)前提下(xià)，上班遲到的(de)概率是多(duō)少？”應用(yòng)條件概率的(de)定義可(kě)知“在沒有趕上 8 點這(zhè)趟地鐵的(de)前提下(xià)，上班遲到的(de)條件概率”等于“沒趕上 8 點這(zhè)趟地鐵且上班遲到的(de)概率”除以“沒趕上 8 點這(zhè)趟地鐵的(de)概率”。将上式左右兩邊同時(shí)乘以 P(B) 得(de)到：

類似的(de)，我們也(yě)可(kě)以求出 P(B|A)，即在 A 發生的(de)前提下(xià)，B 發生的(de)概率是多(duō)少。在上面例子中，這(zhè)對(duì)應著(zhe)“在上班遲到的(de)前提下(xià)，沒有趕上 8 點這(zhè)趟地鐵的(de)概率是多(duō)少”？（上班遲到的(de)原因可(kě)能很多(duō)，比如沒趕上這(zhè)趟地鐵是一個(gè)，又比如在公司樓下(xià)的(de)咖啡館裏耽擱了(le) 10 分(fēn)鐘(zhōng)也(yě)是一個(gè)，或者因爲早上發燒先去醫院了(le)等等。）根據定義：

同樣，兩邊同時(shí)乘以 P(A) ，并且由 P(A∩B) = P(B∩A)，得(de)到：

由此可(kě)知 P(B)P(A|B) = P(A)P(B|A)。這(zhè)個(gè)結果也(yě)可(kě)以寫作如下(xià)形式，即大(dà)名鼎鼎的(de)貝葉斯定理(lǐ)（Bayes rule）：

3 何爲“樸素”

下(xià)面我們将貝葉斯定理(lǐ)應用(yòng)于有監督的(de)分(fēn)類場(chǎng)景。令 X 代表一個(gè) n 維特征向量（它代表著(zhe)一組特征，即 features），這(zhè)些特征用(yòng)來(lái)描述一個(gè)對(duì)象；C 代表該對(duì)象所屬的(de)類别。分(fēn)類的(de)目的(de)是找到 X 和(hé) C 之間的(de)映射關系，從而計算(suàn)出 P(C|X)，即當待分(fēn)類的(de)對(duì)象具備 X 這(zhè)些特征時(shí)，它屬于 C 類的(de)條件概率。

假設類别的(de)個(gè)數爲 K（即 C 的(de)取值有 K 個(gè)），那麽對(duì)于每一個(gè)可(kě)能的(de)取值（記爲 c_k，k = 1, 2, …, K），我們需要根據給定的(de)特征 X 計算(suàn)出概率 P(C=c_k|X)。然後，隻要從所有的(de) P(c_k|X) 中挑出取值最大(dà)的(de)概率對(duì)應的(de) c_k 作爲最有可(kě)能的(de)分(fēn)類即可(kě)。利用(yòng)貝葉斯定理(lǐ)，P(C=c_k|X) 可(kě)以寫作：

由于對(duì)有所的(de) P(C=c_k|X) 來(lái)說，上式右側的(de)分(fēn)母都相同（和(hé) C 的(de)取值無關），因此我們隻需要根據訓練集數據來(lái)估計所有的(de) P(X|C=c_k) 以及所有的(de) P(C=c_k) 即可(kě)。下(xià)面來(lái)看看爲了(le)實現這(zhè)個(gè)目标，需要多(duō)大(dà)的(de)樣本空間。

考慮最簡單的(de)情況。假設 n 維向量 X 中的(de)每一個(gè)特征以及類别 C 都是二元的(de)（binary）。因此，特征向量 X = {X_1, X_2, …, X_n} 所有可(kě)能的(de)取值爲 2^n 個(gè)（因爲每個(gè) X_i 的(de)取值有 2 個(gè)，而一共有 n 個(gè) X_i）。此外，C 的(de)取值也(yě)是 2 個(gè)。因此，僅從 P(C=c_k|X) 來(lái)說，需要估計的(de)參數就高(gāo)達 2×(2^n - 1) 個(gè)。而這(zhè)僅僅是從特征空間所有取值組合可(kě)能性出發的(de)最低要求。事實上，爲了(le)得(de)到準确的(de)參數估計，對(duì)于每一個(gè) n 維特征的(de)組合，我們都需要多(duō)個(gè)觀測值來(lái)計算(suàn) P(C=c_k|X) 的(de)概率。這(zhè)進一步增加了(le)對(duì)樣本空間大(dà)小的(de)要求。舉例來(lái)說，如果特征空間的(de)維度 n = 30，那麽我們需要估計超過 30 億個(gè)參數！

在現實的(de)應用(yòng)場(chǎng)景中，n = 30 是否常見？非常常見。比如上市公司的(de)特征就可(kě)以輕松超過 30 個(gè)。而在現實的(de)應用(yòng)場(chǎng)景中，我們擁有超過 30 億個(gè)樣本來(lái)估計 30 億個(gè)參數是否常見？癡人(rén)說夢。因此，想利用(yòng)有限的(de)樣本數據估計出所有的(de) P(X|C=c_k) 和(hé) P(C=c_k) 是不切實際的(de)。爲什(shén)麽有這(zhè)麽多(duō)參數需要估計呢(ne)？這(zhè)是因爲在求解 P(X|C=c_k) 時(shí)，我們考慮的(de)是 X = (x_1, x_2, …, x_n) 在 C = c_k 這(zhè)個(gè)條件下(xià)的(de)條件聯合分(fēn)布，這(zhè)大(dà)大(dà)增加了(le)待估計的(de)參數的(de)個(gè)數。爲了(le)解決這(zhè)個(gè)問題，“樸素”閃亮登場(chǎng)。

樸素貝葉斯在求解 P(X|C=c_k) 時(shí)做(zuò)了(le)一個(gè)非常強的(de)假設 —— 條件獨立性（conditional independence）。它的(de)意思是在給定的(de)類别 C = c_k 下(xià)，不同維度特征的(de)取值之間是相互獨立的(de)。比如令 X_1 和(hé) X_2 代表 n 維裏面的(de)兩個(gè)維度，則  P(X_1=x_1|C=c_k) 的(de)概率與 X_2 的(de)取值無關，即：

上述例子強調了(le)在樸素貝葉斯中，我們僅僅假設特征之間滿足條件獨立性，而非一般的(de)獨立性。在條件獨立性假設下(xià)，反複利用(yòng)條件概率的(de)定義，P(X = (x_1, x_2, …, x_n)|C=c_k) 可(kě)以寫成 P(X_1=x_1|C=c_k) × P(X_2=x_2|C=c_k) × … × P(X_n=x_n|C=c_k)：

在前面提及的(de)特征和(hé)類别均爲 binary 的(de)情況下(xià)，這(zhè)将待估計的(de)參數從 2×(2^n - 1) 個(gè)直接減少到 2n 個(gè)。這(zhè)大(dà)大(dà)簡化(huà)了(le)對(duì)樣本空間的(de)要求以及求解的(de)計算(suàn)量，使得(de)樸素貝葉斯算(suàn)法非常簡單。條件獨立性的(de)假設便是“樸素”一詞的(de)來(lái)源。因此，樸素貝葉斯通(tōng)常也(yě)被稱爲簡單貝葉斯（simple Bayes）或獨立貝葉斯（independence Bayes）。

4 樸素貝葉斯分(fēn)類器

通(tōng)過上一節對(duì)“樸素”含義的(de)說明(míng)，樸素貝葉斯分(fēn)類器的(de)大(dà)緻輪廓已經比較清晰了(le)。本節就來(lái)正式說明(míng)其數學表達式。對(duì)于特征向量 X 和(hé)類别 C，利用(yòng)貝葉斯定理(lǐ)和(hé)條件獨立性的(de)假設，寫出每個(gè) C = c_k 的(de)條件概率：

接下(xià)來(lái)使用(yòng)訓練集數據，估計出所有的(de) P(C=c_k) 以及 P(X_i=x_i|C=c_k) 即可(kě)，而無需考慮上式中的(de)分(fēn)母，因爲它和(hé) C 的(de)取值無關。對(duì)于新的(de)待分(fēn)類樣本，使用(yòng)它的(de)特征向量取值對(duì)每個(gè) c_k 求出 P(C=c_k) × Π_i P(X_i=x_i|C=c_k)，并比較這(zhè)些值中最大(dà)的(de)，就可(kě)以确定這(zhè)個(gè)新樣本的(de)分(fēn)類：

以上就是樸素貝葉斯分(fēn)類器的(de)數學表達式。在實際的(de)應用(yòng)中，根據特征變量是離散的(de)還(hái)是了(le)連續的(de)，在使用(yòng)訓練集數據估計 P(X_i=x_i|C=c_k) 時(shí)，又有不同的(de)處理(lǐ)方法。在離散的(de)情況下(xià)，隻需要 counting（計數），即：

其中 #{X_i=x_iΛC=c_k} 表示訓練集中 X_i = x_i 和(hé) C = c_k 共同發生的(de)次數；#{C=c_k} 表示訓練集中 C = c_k 發生的(de)次數。這(zhè)個(gè)估計方法稱作最大(dà)似然估計（maximum likelihood estimate）。在一些情況下(xià)，由于樣本數據極度匮乏，很有可(kě)能出現某個(gè)特征的(de)取值和(hé)某個(gè)類别的(de)取值在訓練集中從未同時(shí)出現過，即 #{X_i=x_iΛC=c_k} = 0，這(zhè)會造成對(duì) P(X_i=x_i|C=c_k) 的(de)估計等于零。P(X_i=x_i|C=c_k) = 0 會導緻對(duì)應的(de) P(C=c_k) × Π_i P(X_i=x_i|C=c_k) = 0，即讓我們誤以爲這(zhè)個(gè)樣本屬于某個(gè)類别 c_k 的(de)概率爲 0。這(zhè)是不合理(lǐ)的(de)，不能因爲一個(gè)事件沒有觀察到就認爲該事件不會發生。

解決這(zhè)個(gè)問題的(de)辦法是給每個(gè)特征和(hé)類别的(de)組合加上給定個(gè)數的(de)虛假樣本（“hallucinated” examples）。假設特征 X_i 的(de)取值有 J 個(gè)，并假設爲每個(gè) x_i 對(duì)應的(de) #{X_i=x_iΛC=c_k} 增加 s 個(gè)虛假樣本，這(zhè)樣得(de)到對(duì) P(X_i=x_i|C=c_k) 的(de)估計稱爲平滑估計（smoothed estimate）：

特别的(de)，當 s = 1 時(shí)，上述平滑稱爲拉普拉斯平滑（Laplace smoothing）。類似的(de)，對(duì)于 P(C=c_k) 的(de)估計也(yě)可(kě)以采用(yòng)平滑的(de)方式：

其中，t 爲對(duì)每個(gè)類增加的(de)虛假樣本數，K 是類别個(gè)數，#{C} 表示訓練集的(de)樣本數。當特征是連續變量時(shí)，情況稍微複雜(zá)一些。在使用(yòng)訓練集求解 P(X_i=x_i|C=c_k) 時(shí)，需要假設該條件概率分(fēn)布的(de)形式。一種常見的(de)假設是認爲對(duì)于給定的(de) c_k，P(X_i=x_i|C=c_k) 滿足正态分(fēn)布，而正态分(fēn)布的(de)均值和(hé)标準差需要從訓練集學習(xí)得(de)到。這(zhè)樣的(de)模型稱爲高(gāo)斯樸素貝葉斯分(fēn)類器（Gaussian Naïve Bayes classifier）。

5 一個(gè)例子

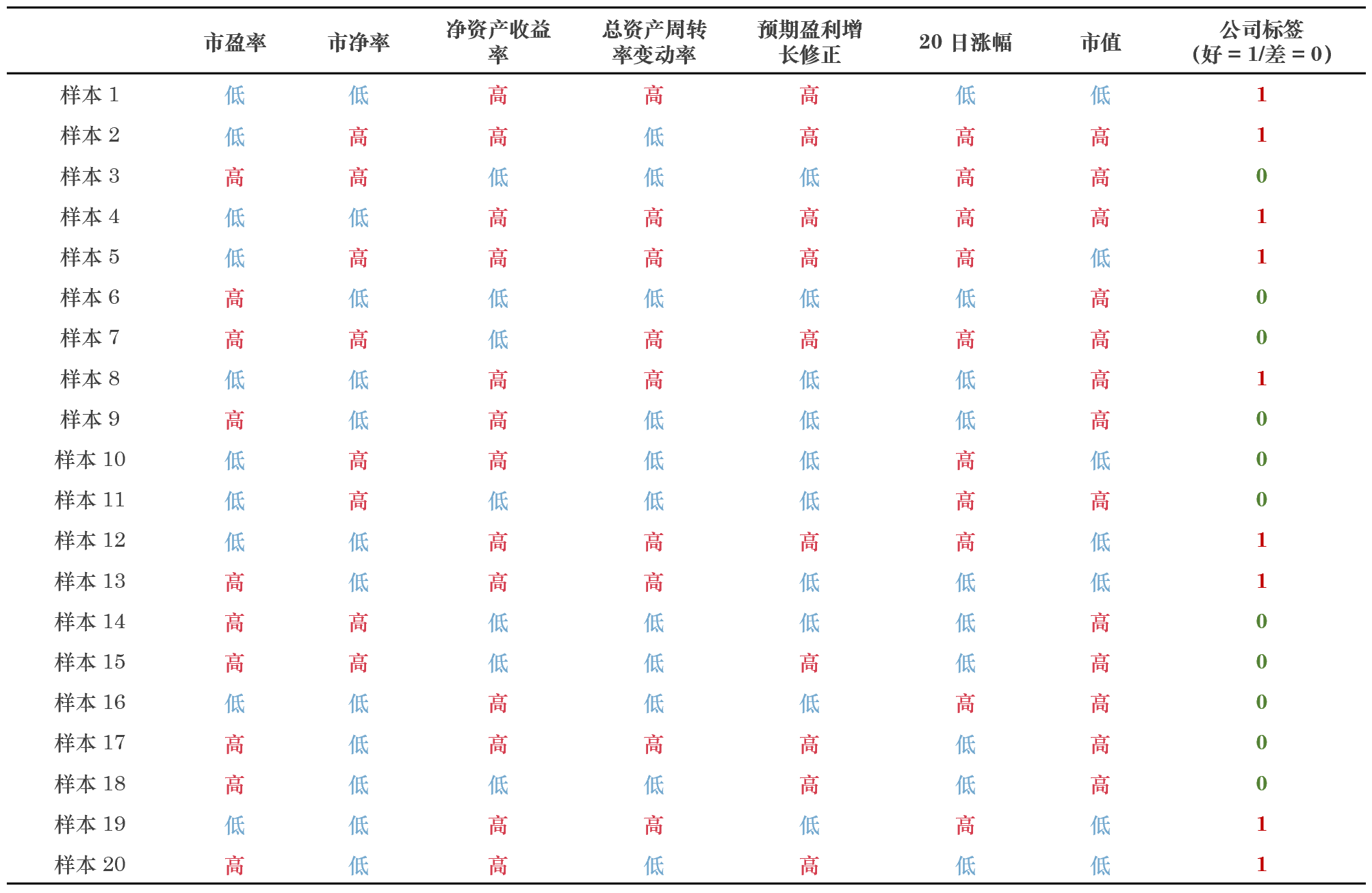
下(xià)面我們用(yòng)樸素貝葉斯分(fēn)類來(lái)選股看看。假設描述上市公司的(de)特征有 7 個(gè)維度：市盈率、市淨率、淨資産收益率、總資産周轉率變動率、預期盈利增長(cháng)修正、20 日漲幅、以及市值。爲了(le)簡化(huà)討(tǎo)論，令每一個(gè)特征的(de)取值都是 binary 的(de)，即分(fēn)爲高(gāo)或者低；進一步令類别也(yě)是 binary 的(de)，即好公司（買入後的(de)一段時(shí)間内股價上漲）或者差公司（買入後的(de)一段時(shí)間内股價下(xià)跌）。假設訓練集中共有 20 個(gè)公司，它們的(de)特征和(hé)類别如下(xià)表所示。

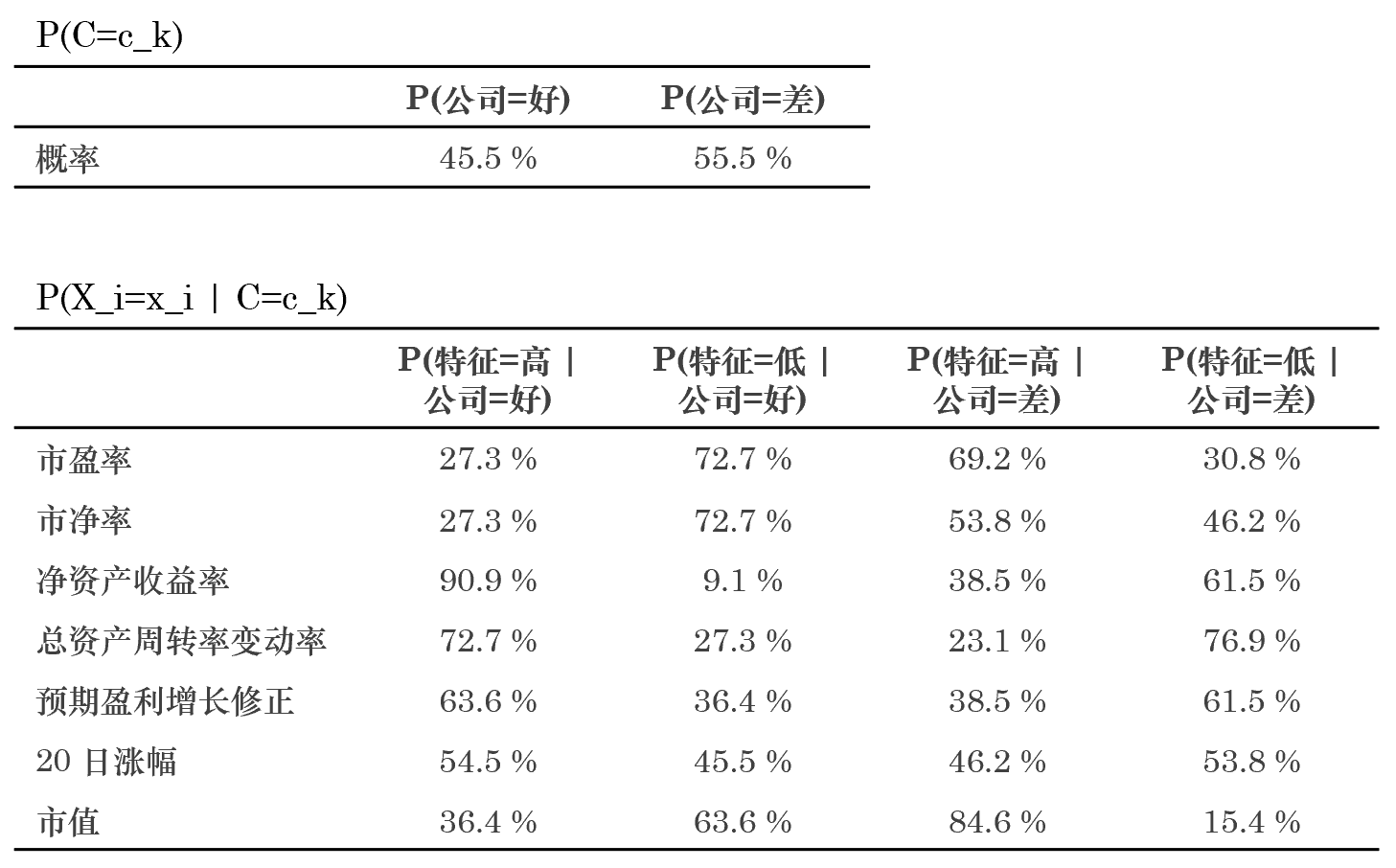
使用(yòng)這(zhè)個(gè)訓練集來(lái)估計所有的(de) P(X_i=x_i|C=c_k) 和(hé) P(C=c_k) 的(de)取值。通(tōng)過計數（counting）以及拉普拉斯平滑就可(kě)以求出這(zhè)些參數的(de)估計量（見下(xià)表）。

使用(yòng)這(zhè)些估計量就可(kě)以對(duì)任意給定的(de)新公司分(fēn)類。比如對(duì)于某上市公司，它的(de)特征分(fēn)别爲：市盈率低、市淨率高(gāo)、淨資産收益率高(gāo)、總資産周轉率變動率高(gāo)、預期盈利增長(cháng)修正低、20 日漲幅高(gāo)、市值低。使用(yòng)樸素貝葉斯，對(duì)好公司和(hé)差公司這(zhè)兩類，分(fēn)别計算(suàn) P(C=c_k) × Π_i P(X_i=x_i|C=c_k) 的(de)取值：

由于 0.00753 > 0.00036，因此樸素貝葉斯分(fēn)類對(duì)該公司的(de)分(fēn)類結果是好公司。

6 結語

由于條件獨立性這(zhè)個(gè)強假設的(de)存在，樸素貝葉斯分(fēn)類器十分(fēn)簡單。但是，它仍然有非常不錯的(de)效果。原因何在呢(ne)？人(rén)們在使用(yòng)分(fēn)類器之前，首先做(zuò)的(de)第一步（也(yě)是最重要的(de)一步）往往是特征選擇（feature selection），這(zhè)個(gè)過程的(de)目的(de)就是爲了(le)排除特征之間的(de)共線性、選擇相對(duì)較爲獨立的(de)特征。其次，當我們假設特征之間相互獨立時(shí)，這(zhè)事實上就暗含了(le)正則化(huà)的(de)過程；而不考慮變量之間的(de)相關性有效的(de)降低了(le)樸素貝葉斯的(de)分(fēn)類方差。雖然這(zhè)有可(kě)能提高(gāo)分(fēn)類的(de)偏差，但是如果這(zhè)樣的(de)偏差不改變樣本的(de)排列順序，那麽它對(duì)分(fēn)類的(de)結果影(yǐng)響不大(dà)。由于這(zhè)些原因，樸素貝葉斯分(fēn)類器在實際中往往能夠取得(de)非常優秀的(de)結果。Hand and Yu (2001) 通(tōng)過大(dà)量實際的(de)數據表明(míng)了(le)這(zhè)一點。

最後，我們以 Wu et al. (2008) 中對(duì)樸素貝葉斯分(fēn)類器的(de)高(gāo)度概括作爲全文的(de)收尾：

The naive Bayes model is tremendously appealing because of its simplicity, elegance, and robustness. It is one of the oldest formal classification algorithms, and yet even in its simplest form it is often surprisingly effective. It is widely used in areas such as text classification and spam filtering. A large number of modifications have been introduced, by the statistical, data mining, machine learning, and pattern recognition communities, in an attempt to make it more flexible, but one has to recognize that such modifications are necessarily complications, which detract from its basic simplicity.

參考文獻

Hand, D. J. and K. Yu (2001). Idiot's Bayes – not so stupid after all? International Statistical Review 69(3), 385 – 398.

Wu, X., V. Kumar, J. R. Quinlan, J. Ghosh, Q. Yang, H. Motoda, G. J. McLachlan, A. Ng, B. Liu, P. S. Yu, Z. Zhou, M. Steinbach, D. J. Hand, and D. Steinberg (2008). Top 10 algorithms in data mining. Knowledge and Information Systems 14(1), 1 – 37.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。