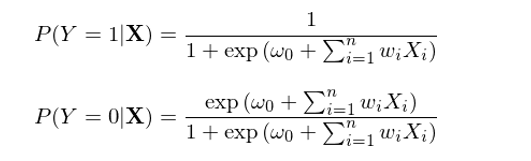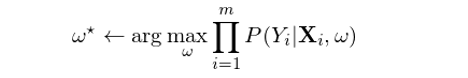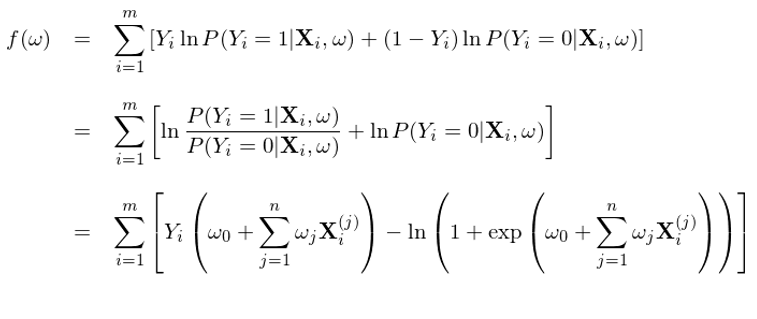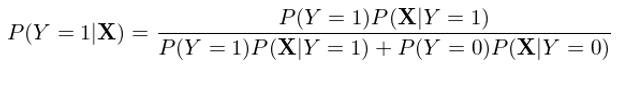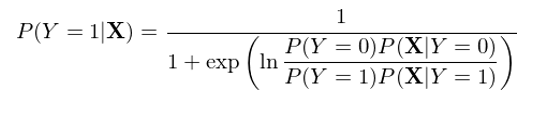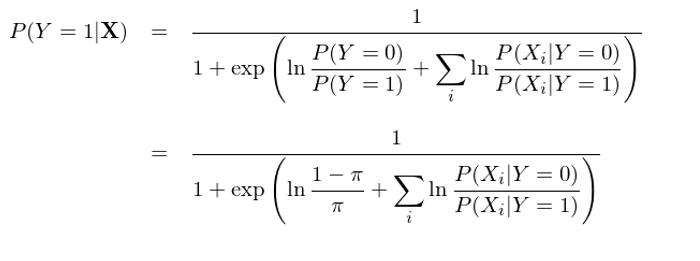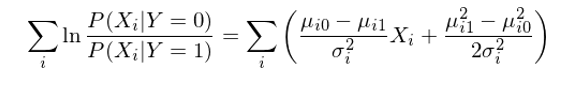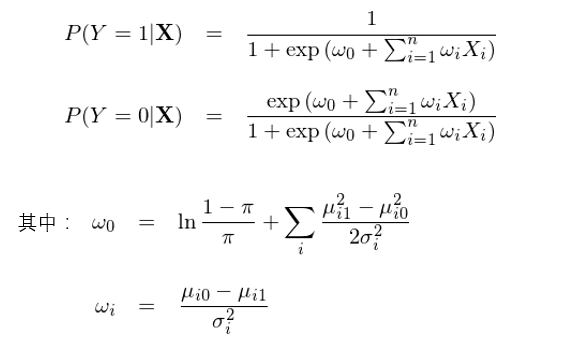邏輯回歸 vs 樸素貝葉斯

作者：石川

摘要：本文通(tōng)過簡單對(duì)比邏輯回歸和(hé)高(gāo)斯樸素貝葉斯來(lái)說明(míng)判别模型和(hé)生成模型的(de)區(qū)别。這(zhè)兩類模型的(de)效果與訓練集的(de)大(dà)小有關。

1 引言

上期的(de)量化(huà)核武研究專題介紹了(le)《樸素貝葉斯分(fēn)類器》。趁熱(rè)打鐵，本期再來(lái)聊聊它。特别的(de)，我們把樸素貝葉斯大(dà)類中的(de)高(gāo)斯樸素貝葉斯和(hé)邏輯回歸比較比較。《邏輯回歸，很有邏輯》一文簡單介紹了(le)邏輯回歸的(de)原理(lǐ)（并且用(yòng)中證 500 的(de)成分(fēn)股進行了(le)一個(gè)非常簡單的(de)實證）。

邏輯回歸 vs 高(gāo)斯樸素貝葉斯，這(zhè)其實代表這(zhè)兩類模型的(de) PK。邏輯回歸是判别模型（discriminative model）的(de)代表，而樸素貝葉斯是生成模型（generative model）的(de)代表。更有意思的(de)是，通(tōng)過一定的(de)數學推導可(kě)以看出，高(gāo)斯樸素貝葉斯在求解 P(Y|X) —— 其中 X 爲 n 維特征向量、Y 爲類别标識 —— 時(shí)具有和(hé)邏輯回歸一樣的(de)數學表達式（當然僅僅是解析表達式一緻，而它們背後對(duì)模型參數的(de)求解方法完全不同）。

下(xià)文首先簡要回顧一下(xià)邏輯回歸，其次會推導高(gāo)斯樸素貝葉斯的(de)表達式。之後，通(tōng)過對(duì)比這(zhè)二者來(lái)解釋判别模型和(hé)生成模型的(de)區(qū)别。從評價一個(gè)分(fēn)類器在樣本外準确性的(de) generalization error 來(lái)說，判别模型和(hé)生成模型各有千秋。雖然學術界和(hé)業界普遍認爲判别模型的(de)精度更高(gāo)，但 Ng and Jordan (2002) 通(tōng)過理(lǐ)論和(hé)實證表明(míng)，在訓練集樣本數量很少的(de)情況下(xià)，生成模型的(de)效果往往優于判别模型。

2 邏輯回歸

本節以二元分(fēn)類爲例簡要介紹邏輯回歸。在二元邏輯回歸中，每個(gè)樣本點都屬于 0 或者 1 這(zhè)兩類中的(de)某一類。回歸模型根據樣本點的(de)特征計算(suàn)該樣本點屬于每一類的(de)條件概率，即 P(Y|X)。與樸素貝葉斯不同，邏輯回歸直接對(duì) P(Y|X) 建模求解，而不需要先求出 P(X|Y) 和(hé) P(Y)、再應用(yòng)貝葉斯定理(lǐ)。在求解 P(Y|X) 時(shí)，邏輯回歸假定了(le)如下(xià)的(de)參數化(huà)形式：

其中，函數 h(z) ≡ 1 / (1 + exp(-z)) 被稱爲邏輯函數（logistic function）或 sigmoid 函數（因爲 h(z) 形如 S 曲線）；它的(de)取值範圍在 0 和(hé) 1 之間。邏輯回歸的(de)目的(de)是通(tōng)過訓練集數據找到最優的(de)參數 w 使得(de)分(fēn)類結果盡量同時(shí)滿足如下(xià)目标：

由邏輯函數的(de)性質可(kě)知，樣本點的(de)分(fēn)類取決于特征向量 X 按 w 線性組合後得(de)到的(de)标量與 0 的(de)關系，即滿足 w'X = 0 的(de) X 構成了(le)分(fēn)類的(de)超平面。該标量大(dà)于 0 意味著(zhe) P(Y=0|X) > P(Y=1|X)，即該樣本點應該被分(fēn)到類别 0，反之爲類别 1。在決定最優參數 w 時(shí)，一個(gè)合理(lǐ)的(de)目标是在訓練模型時(shí)最大(dà)化(huà)條件似然性。假設訓練集共有 m 對(duì)兒(ér)樣本 {(X_i, Y_i), i = 1, 2, …, m}，則最優的(de) w* 應滿足：

兩邊取對(duì)數（目的(de)是将右側求積變成求和(hé)）、利用(yòng) Y_i 僅能取 0 或者 1 這(zhè)個(gè)事實、并将 P(Y|X) 寫成邏輯回歸的(de)邏輯函數，就可(kě)以得(de)到求解 w 時(shí)的(de)目标函數 f(w)：

其中 X_i^(j) 爲第 i 個(gè)樣本的(de)第 j 個(gè)特征的(de)取值。該目标函數同時(shí)考慮了(le) 1 和(hé) 0 兩類分(fēn)類的(de)準确性。使用(yòng)訓練集對(duì)該模型訓練，找到最優的(de) w*，使得(de)該目标函數 f(w*) 最大(dà)，這(zhè)就是邏輯回歸模型的(de)學習(xí)過程。最優化(huà) f(w) 可(kě)以采用(yòng)梯度上升（gradient ascent），爲此隻需要計算(suàn)出 f 的(de)梯度 ∇f(w)。由于 f(w) 是 w 的(de)凹函數，該方法一定能保證找到全局最優解。

3 高(gāo)斯樸素貝葉斯分(fēn)類器

樸素貝葉斯分(fēn)類器是一類分(fēn)類器的(de)總稱，它們均利用(yòng)了(le)貝葉斯定理(lǐ)并假設特征之間的(de)條件獨立性（詳見《樸素貝葉斯分(fēn)類器》）。高(gāo)斯樸素貝葉斯（Gaussian Naïve Bayes，GNB）分(fēn)類器是其中常見的(de)一種。考慮滿足如下(xià)假設的(de) GNB：

與邏輯回歸直接對(duì) P(Y|X) 建模不同，高(gāo)斯樸素貝葉斯對(duì) P(X|Y) 和(hé) P(Y) 建模，然後利用(yòng)貝葉斯定理(lǐ)反推 P(Y|X)。以 Y = 1 爲例有：

在上式右側的(de)分(fēn)母中，我們将 P(X) 使用(yòng)全概率公式（law of total probability）寫成了(le)分(fēn)解的(de)形式，這(zhè)是爲了(le)下(xià)面進一步的(de)推導。将上式右側分(fēn)子分(fēn)母同時(shí)除以分(fēn)子，并利用(yòng)經典的(de) exp 和(hé) ln 配對(duì)變化(huà)可(kě)得(de)：

通(tōng)過特征之間的(de)條件獨立性（即“樸素”），上式可(kě)以進一步變化(huà)得(de)到：

現在，P(Y=1|X) 的(de)表達式已經看著(zhe)和(hé)邏輯回歸的(de)表達式類似了(le)，當然還(hái)有一些差異，這(zhè)個(gè)差異就是分(fēn)母上的(de)那一坨求和(hé)項是概率的(de)形式而不是 X_i 的(de)線性組合的(de)形式。好消息是利用(yòng)條件正态分(fēn)布的(de)分(fēn)布函數，這(zhè)一坨求和(hé)可(kě)以輕松的(de)轉變成 X_i 的(de)線性組合（推導略）：

将變換後的(de)求和(hé)項帶入到 P(Y=1|X) 的(de)表達式中，終于我們得(de)到了(le)想要的(de)結果：

我們看到，通(tōng)過上面這(zhè)一大(dà)串數學變換，高(gāo)斯樸素貝葉斯下(xià)的(de) P(Y=1|X) 和(hé) P(Y=0|X) 的(de)解析式和(hé)邏輯回歸完全一緻。但是，千萬不要誤解，雖然表達式一緻，這(zhè)二者求解最優參數向量 w 的(de)邏輯卻不同。在邏輯回歸中，通(tōng)過最大(dà)化(huà)目标函數 f(w) 直接求解最優的(de)參數 w；而在 GNB 中，w 的(de)形式是給定的(de)，它由條件正态分(fēn)布的(de)均值和(hé)方差決定，而訓練集的(de)作用(yòng)是估計這(zhè)些均值和(hé)方差，而非直接估計 w。這(zhè)事實上引出了(le)判别模型和(hé)生成模型的(de)區(qū)别。

4 判别模型 vs 生成模型

在邏輯回歸中，我們根據樣本數據直接估計 P(Y|X)。利用(yòng)給定的(de)函數形式 —— 這(zhè)裏指的(de)是邏輯函數 1 / (1 + exp(-z)) —— 找到最優的(de)參數 w。而在高(gāo)斯樸素貝葉斯中，我們有點“多(duō)此一舉”：首先估計 P(X|Y) 和(hé) P(Y)，然後再利用(yòng)貝葉斯定理(lǐ)反推 P(Y|X)。換句話(huà)說，雖然再這(zhè)兩種方法中，P(Y|X) 的(de)解析式一樣，但是樸素貝葉斯無疑比邏輯回歸多(duō)了(le)中間一層，而且這(zhè)層還(hái)使用(yòng)了(le)一個(gè)非常強的(de)假設 —— 特征間的(de)條件獨立性。因此，從直覺上來(lái)說，樸素貝葉斯确實“多(duō)此一舉”，我們傾向于認爲它的(de)分(fēn)類效果不如純粹針對(duì) P(Y|X) 建模的(de)邏輯回歸。

先别急著(zhe)下(xià)結論。在樸素貝葉斯中，對(duì) P(X|Y) 和(hé) P(Y) 進行估計實際上是計算(suàn) X 和(hé) Y 的(de)聯合概率分(fēn)布 P(X, Y)。有了(le)這(zhè)個(gè)聯合分(fēn)布，我們就可(kě)以用(yòng)它生成（generate）新的(de)數據，解決更廣泛數據挖掘問題（當然就包括了(le)推導出 P(Y|X)），特别是無監督學習(xí)問題。這(zhè)就是爲什(shén)麽這(zhè)一類模型稱爲生成模型（generative）。它對(duì)特征空間 X 和(hé)類别 Y 的(de)聯合分(fēn)類建模，從而利用(yòng) P(X, Y) 發現 X 和(hé) Y 之間更複雜(zá)的(de)關系。典型的(de)生成模型包括樸素貝葉斯、隐馬爾可(kě)夫等。

而在邏輯回歸（以及其他(tā)判别模型）中，我們僅僅關心條件概率 P(Y|X)，即在給定樣本點特征下(xià) Y 的(de)條件概率是什(shén)麽樣，而非 P(X, Y)。因此它也(yě)就無法回答(dá)任何需要利用(yòng) P(X, Y) 來(lái)計算(suàn)的(de)問題。但是在分(fēn)類和(hé)回歸這(zhè)些通(tōng)常不需要聯合分(fēn)布 P(X, Y) 的(de)領域，判别模型往往會取得(de)更好的(de)效果。大(dà)多(duō)數判别模型都是解決有監督學習(xí)的(de)問題，難以支持無監督學習(xí)。常見的(de)判别模型包括邏輯回歸、支持向量機、随機森林(lín)等。

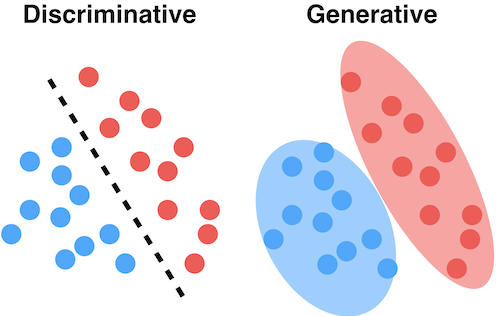
下(xià)面兩幅示意圖很好的(de)說明(míng)了(le)判别模型和(hé)生成模型的(de)區(qū)别和(hé)聯系。假設紅色和(hé)藍色圓點表示屬于不同兩類的(de)訓練集樣本。判别模型的(de)目标是找到一個(gè)最能夠區(qū)分(fēn)它們的(de)邊界，而不在乎每一類中的(de)樣本點是如何分(fēn)布的(de)；而生成模型首先對(duì)各類中樣本的(de)分(fēn)布建模，即求解 P(X|Y)。

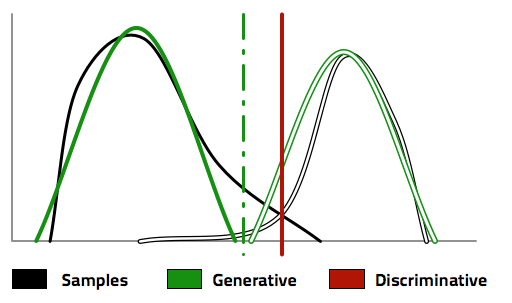
有了(le) P(X|Y) 以及 P(Y)，生成模型利用(yòng)貝葉斯定理(lǐ)，反推出 P(Y|X)，從而找到分(fēn)類的(de)邊界，正如下(xià)圖中的(de)綠色虛線。爲了(le)得(de)到這(zhè)個(gè)分(fēn)類邊界，首先是求出了(le)不同兩類的(de)分(fēn)布 P(X|Y)，如圖中的(de)綠色實線和(hé)綠色空心線所示。反觀判别模型，它更直接、更純粹；直接根據樣本數據找到一條分(fēn)類邊界，如圖中的(de)紅色實線所示。

再回到本文的(de)對(duì)象 —— 高(gāo)斯樸素貝葉斯和(hé)邏輯回歸。可(kě)以證明(míng)，當特征之間确實滿足條件獨立性時(shí)，随著(zhe)訓練集樣本個(gè)數的(de)增多(duō)，在極限情況下(xià)，高(gāo)斯樸素貝葉斯和(hé)邏輯回歸求出的(de)最優參數 w 是一緻的(de)。然而，當這(zhè)個(gè)假設不成立時(shí)，樸素貝葉斯的(de)這(zhè)個(gè)假設就會對(duì)分(fēn)類的(de)準确性造成負面的(de)影(yǐng)響。而邏輯回歸的(de)最大(dà)化(huà)條件似然性求解則可(kě)以根據數據中非獨立性來(lái)調節最優參數 w。從這(zhè)個(gè)角度來(lái)說，邏輯回歸優于（高(gāo)斯）樸素貝葉斯也(yě)就不足爲奇。

關于判别模型和(hé)生成模型的(de)比較，著名的(de)人(rén)工智能專家 Andrew Ng（吳恩達）和(hé)比吳還(hái)要著名的(de) Michael I. Jordan（也(yě)叫喬丹，但不是打籃球的(de)那位，那個(gè)是 Michael J. Jordan）寫過一篇影(yǐng)響深遠(yuǎn)的(de)文章(zhāng)（Ng and Jordan 2002）。該文以邏輯回歸和(hé)樸素貝葉斯爲例對(duì)比了(le)這(zhè)兩種模型，并指出：

這(zhè)兩點說明(míng)，随著(zhe)訓練集樣本數目的(de)變化(huà)，邏輯回歸和(hé)樸素貝葉斯之間的(de)孰優孰劣會發生改變。當訓練集很小時(shí)（在很多(duō)問題中，訓練集數據非常稀缺），樸素貝葉斯因爲收斂的(de)較快(kuài)，它在樣本外的(de)分(fēn)類精度會高(gāo)于邏輯回歸；而随著(zhe)訓練集樣本數的(de)增多(duō)，由于邏輯回歸的(de)極限誤差更小，因此它最終會戰勝樸素貝葉斯，取得(de)更高(gāo)的(de)分(fēn)類精度。

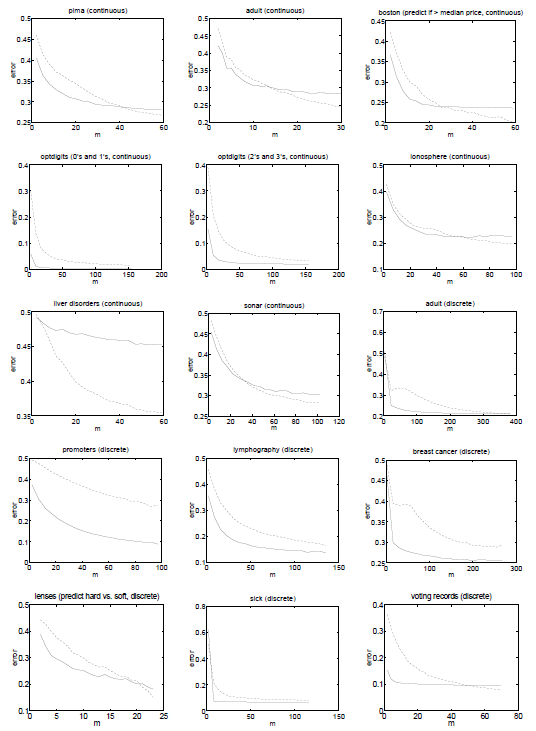
Ng and Jordan (2002) 使用(yòng) 15 個(gè)公開數據集對(duì)上述結論進行了(le)驗證。下(xià)面每一幅圖代表了(le)一個(gè)實驗，其橫坐(zuò)标是訓練集樣本個(gè)數，縱坐(zuò)标爲樣本外的(de)分(fēn)類誤差；虛線表示邏輯回歸的(de)結果、實線表示樸素貝葉斯的(de)結果。從大(dà)部分(fēn)實驗中可(kě)以觀察到，當訓練集樣本數較少時(shí)，實線處于虛線下(xià)方，說明(míng)樸素貝葉斯優于邏輯回歸（它的(de)極限誤差雖然高(gāo)，但是它收斂的(de)更快(kuài)）；而随著(zhe)樣本個(gè)數的(de)增加，虛線最終會下(xià)穿實線，意味著(zhe)邏輯回歸最終戰勝了(le)樸素貝葉斯。

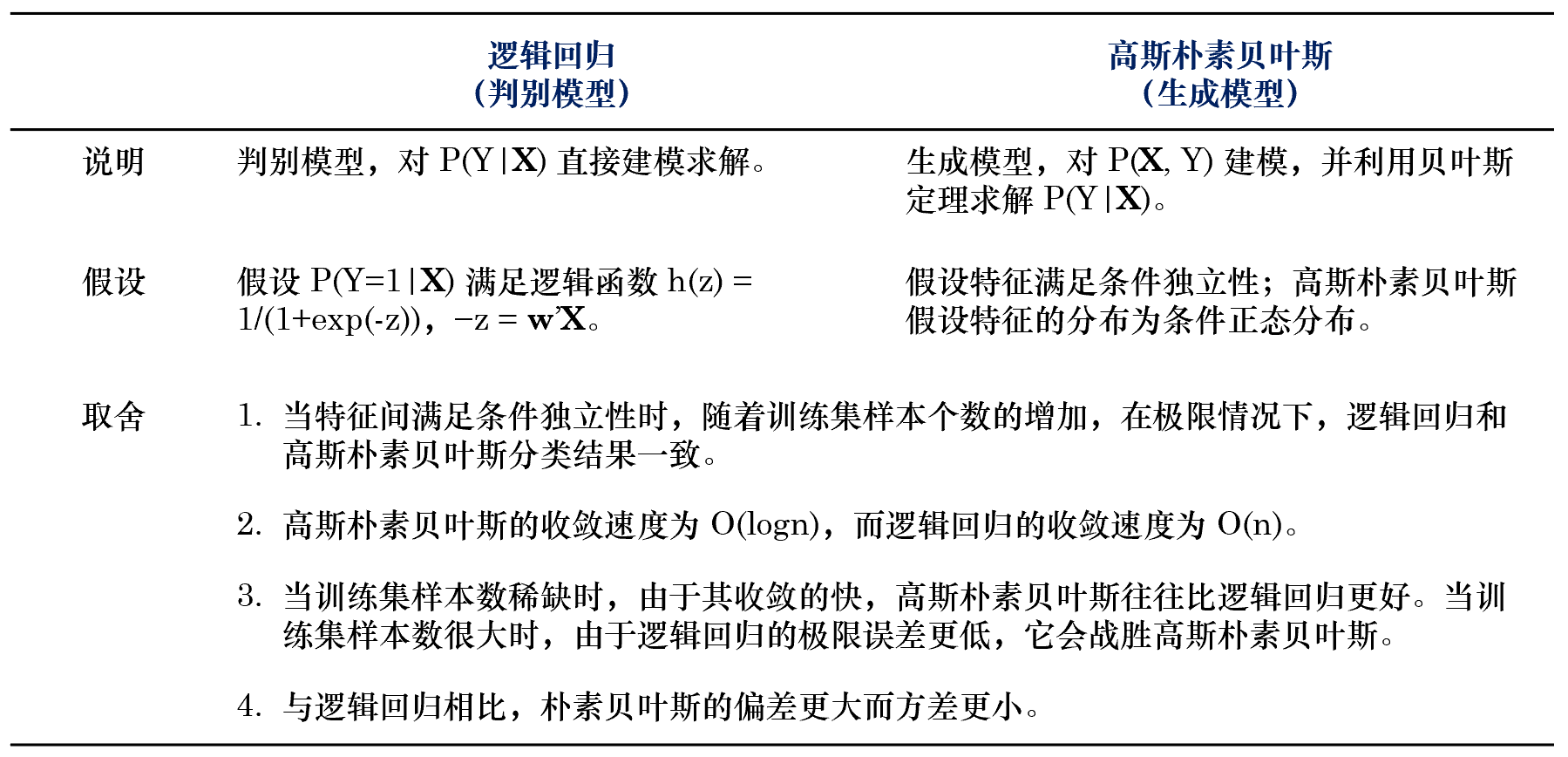
最後，我們把邏輯回歸和(hé)樸素貝葉斯的(de)區(qū)别彙總于下(xià)表。

5 結語

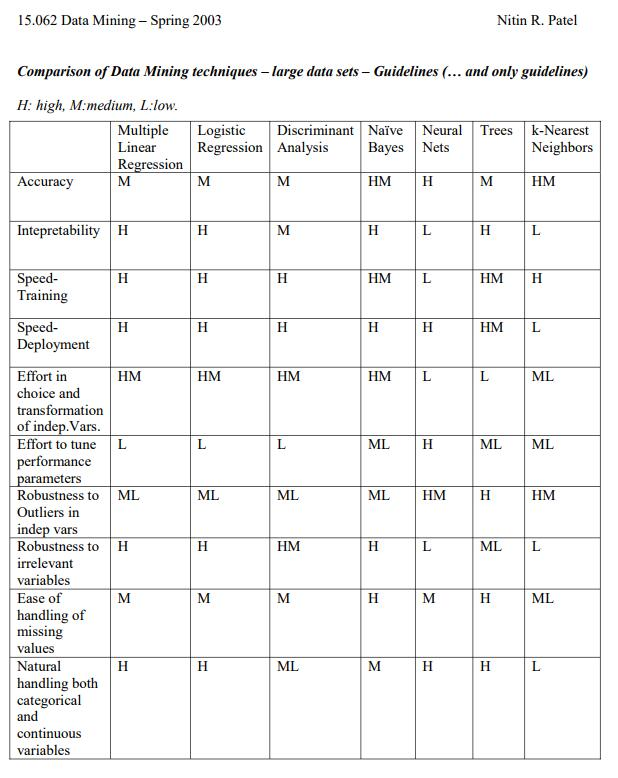
判别模型和(hé)生成模型各有千秋。對(duì)于判别模型，由于參數個(gè)數較少，所需的(de)樣本個(gè)數也(yě)要少一些。但是生成模型可(kě)以讓我們回答(dá)更複雜(zá)的(de)問題，更深入的(de)挖掘 X 和(hé) Y 之間的(de)關系。“紙上得(de)來(lái)終覺淺，絕知此事要躬行”。爲了(le)比較高(gāo)斯樸素貝葉斯和(hé)邏輯回歸在選股上的(de)效果，我們将在接下(xià)來(lái)用(yòng)中證 500 的(de)成分(fēn)股做(zuò)一些簡單的(de)實證，并把結果彙總于今後的(de)文章(zhāng)中。最後，下(xià)面這(zhè)張圖來(lái)自麻省理(lǐ)工學院的(de)數據發掘課（不過要注意是 2003 年的(de)）。它從不同的(de)維度比較了(le)一些常見的(de)數據挖掘算(suàn)法，這(zhè)其中也(yě)包括今天的(de)主角邏輯回歸和(hé)樸素貝葉斯。這(zhè)些結果是針對(duì)大(dà)數據集的(de)，但仍然可(kě)以作爲一個(gè)選擇的(de)參考，不過也(yě)僅僅是個(gè)參考。在實際問題中，隻有充分(fēn)了(le)解了(le)待分(fēn)析的(de)數據，才有可(kě)能選擇最适當的(de)模型。

參考文獻

Ng, A. Y. and M. I. Jordan (2002). On Discriminative vs. Generative Classifiers: A comparison of logistic regression and naive Bayes. In T. G. Dietterich, S. Becker and Z. Ghahramani (Eds), Advances in Neural Information Processing Systems, Vol. 14, MIT Press, 841 – 848.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。