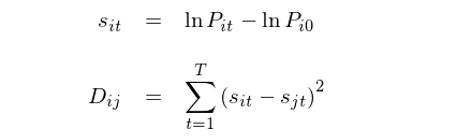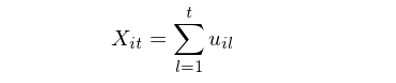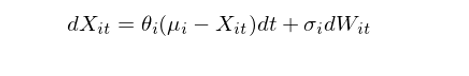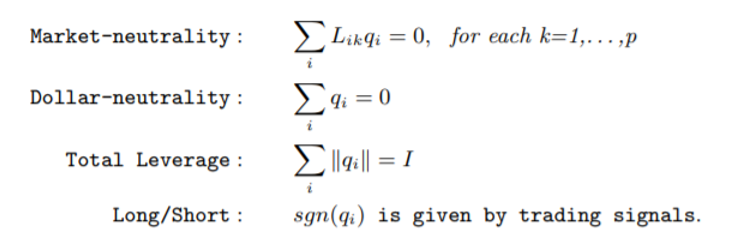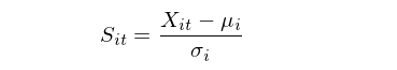次世代均值回歸策略

作者：石川

多(duō)品種構建的(de)價差很難滿足一價定理(lǐ)、不易回歸；針對(duì)這(zhè)類價差的(de)統計套利策略的(de)風險收益比很差。本文介紹一種新的(de)均值回歸思路。

1 金融市場(chǎng)的(de)均值回歸

在量化(huà)投資領域，均值回歸（mean reversion）代表著(zhe)一大(dà)類策略。金融市場(chǎng)的(de)均值回歸定義如下(xià)：

In finance, mean reversion is the assumption that a stock's price will tend to move to the average price over time.

我們可(kě)以把上述定義中的(de)“股票(piào)”換成其他(tā)任何投資品。這(zhè)個(gè)定義中最核心的(de)兩個(gè)字是“價格”（而不是投資品的(de)“收益率”）：

請暫停一下(xià)，花幾秒鐘(zhōng)體會一下(xià)上面這(zhè)兩句話(huà)。它們是所有均值回歸策略的(de)核心，也(yě)是本文的(de)核心。先鋒基金（Vanguard）的(de)創始人(rén) John Bogle 曾教導我們說，在金融市場(chǎng)，均值回歸是一條鐵律。确實，投資品的(de)價格不可(kě)能一直漲或者一直跌，拿出任何一段時(shí)間來(lái)看，它似乎總是圍繞著(zhe)局部的(de)均值上下(xià)往複波動，呈現出圍繞著(zhe)均值的(de)回歸運動。但是這(zhè)種程度的(de)回歸對(duì)于在統計上構建一個(gè)有效的(de)量化(huà)策略并沒有太多(duō)的(de)幫助。

在現實中，爲了(le)構建一個(gè)均值回歸策略，我們要求價格的(de)時(shí)間序列滿足平穩性。顯然，單一投資品的(de)價格是很難滿足這(zhè)個(gè)假設的(de)。于是量化(huà)界的(de)小夥伴們便開動腦(nǎo)筋，終于發現雖然單一投資品的(de)價格不滿足均值回歸，但是可(kě)以把多(duō)個(gè)投資品（通(tōng)常是兩個(gè)）線性組合在一起，使它們的(de)價差滿足均值回歸。

配對(duì)交易就是當下(xià)市場(chǎng)上主流的(de)構建均值回歸策略的(de)方法。它通(tōng)常利用(yòng)協整（co-integration）或者價格距離法來(lái)找到這(zhè)樣一對(duì)投資品，并認爲它們的(de)價差會在一定的(de)區(qū)間内往複運動，然後基于價差的(de)統計特性計算(suàn)阈值進行交易，因此這(zhè)種策略通(tōng)常又叫統計套利（statistical arbitrage）。本文介紹一種新的(de)均值回歸思路。不過在此之前，還(hái)是讓我們先來(lái)看看市場(chǎng)上流行的(de)這(zhè)兩種投資品配對(duì)方法。

2 協整

我們都知道收益率序列滿足平穩性，而價格序列不滿足平穩性。收益率滿足平穩性僅僅說明(míng)價格呈現随機遊走，它對(duì)于構建賺錢的(de)投資策略沒什(shén)麽用(yòng)。我們想要的(de)是價格序列呈現出平穩性。但凡事都有一個(gè)例外：雖然單一投資品的(de)價格不滿足平穩性，但有時(shí)把多(duō)個(gè)投資品（通(tōng)常是兩個(gè)）線性組合在一起構成一個(gè)價差序列，該序列滿足平穩性。在數學上，如果多(duō)個(gè)非平穩的(de)時(shí)間序列通(tōng)過線性組合得(de)到一個(gè)平穩的(de)時(shí)間序列，則把滿足這(zhè)種關系稱爲協整（co-integration）。《小心僞回歸發現的(de)假關系》一文介紹了(le)協整發生的(de)原因。對(duì)于兩個(gè)投資品的(de)價格序列，它們的(de)價格都表現出了(le)一定的(de)随機性。如果它們的(de)随機性來(lái)自同一個(gè)随機過程（共同的(de)因素），則說它們滿足協整關系，并可(kě)以通(tōng)過一定的(de)線性組合把這(zhè)個(gè)共同的(de)随機因素剔除掉，而剩下(xià)滿足平穩性的(de)價差序列。在數學上，可(kě)以使用(yòng) ADF test 來(lái)檢驗一個(gè)價差序列是否滿足平穩性。

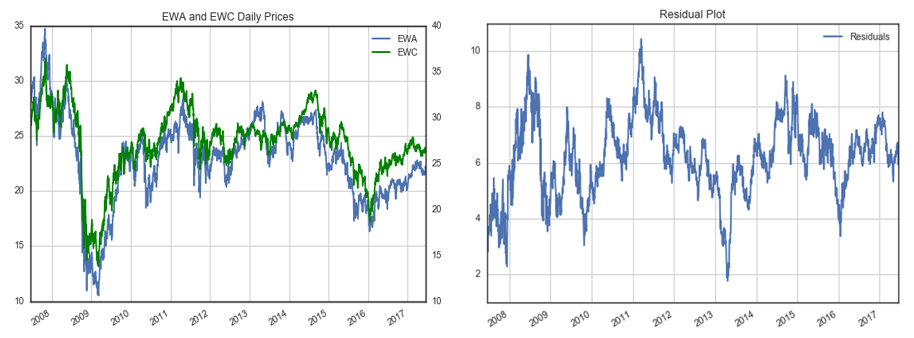
EWA 和(hé) EWC 是一對(duì)兒(ér)滿足協整的(de)經典例子。它們分(fēn)别代表澳大(dà)利亞（EWA）和(hé)加拿大(dà)（EWC）股指的(de)兩個(gè) ETFs。由于這(zhè)兩個(gè)國家的(de)經濟都主要依靠商品，因此可(kě)以認爲這(zhè)兩個(gè)股指的(de)波動來(lái)自共同的(de)因子。下(xià)圖爲這(zhè)兩個(gè) ETFs 的(de)價格序列（左圖）和(hé)回歸得(de)到的(de)價差序列（右圖）。

對(duì)價差進行 ADF 檢驗，得(de)到的(de)統計值爲 -4.09（p-value 爲 0.0065），小于顯著性 1% 對(duì)應的(de)阈值 -3.96，因此在 1% 的(de)顯著性水(shuǐ)平下(xià)拒絕原假設。ADF 檢驗說明(míng)該價差序列滿足平穩性，即 EWA 和(hé) EWC 滿足協整關系。

3 價格距離方法

再來(lái)看看另一種方法：價格距離法。該方法的(de)主要參考文獻是 Gatev et al. (2006)。該文的(de)作者指出，尋找配對(duì)的(de)一種方法是看兩個(gè)投資品标準化(huà)後的(de)價格序列是否足夠接近 —— 即在尋找配對(duì)的(de)形成期這(zhè)兩個(gè)投資品标準化(huà)後的(de)累積價差是否足夠小。關于爲什(shén)麽采用(yòng)這(zhè)種方法找配對(duì)，該文作者給出的(de)解釋如下(xià)：

We use this approach because it best approximates the description of how traders themselves choose pairs. Interviews with pairs traders suggest that they try to find two stocks whose prices "move together".

假設形成期的(de)長(cháng)度爲 T，期内的(de)某投資品 i 的(de)價格序列爲P_i0, P_i1, …, P_iT。在這(zhè)種方法中，首先以 P_i0 爲基準将價格序列轉化(huà)爲對(duì)數價格（這(zhè)相當于把 t 時(shí)刻的(de)價格轉化(huà)成 0 到 t 之間的(de)對(duì)數收益率），然後再計算(suàn) T 期内任意兩個(gè)投資品 i 和(hé) j 的(de)價格偏差平方和(hé)（記爲 D_ij）：

在沒有任何限制的(de)版本中，任意兩個(gè)投資品（比如兩支股票(piào)或者兩種不同的(de)商品期貨）都會被使用(yòng)這(zhè)種方法來(lái)計算(suàn)它們之間價格走勢的(de)相似程度。在有限制的(de)版本中 —— 或者說是從業務上出于防止過拟合的(de)考慮 —— 上述計算(suàn)僅僅被應用(yòng)于同一行業的(de)股票(piào)（比如不同的(de)銀行）或者同一種類的(de)商品期貨（比如農産品或者化(huà)工），以杜絕僅僅因爲巧合而沒有業務邏輯支撐的(de)配對(duì)兒(ér)（Bianchi et al. 2009）。

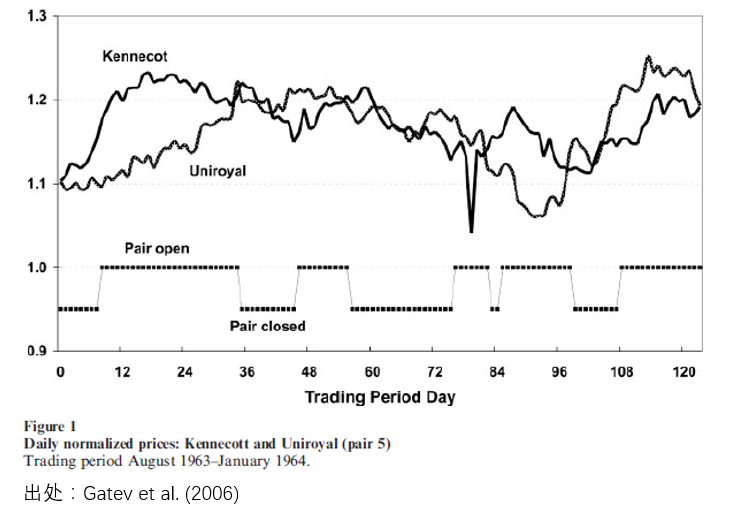
當所有潛在的(de)投資品兩兩計算(suàn)價格距離之後，距離最小的(de)那些配對(duì)兒(ér)就被認爲是滿足價格一起運動，即它們的(de)價差會在未來(lái)一段時(shí)間内呈現均值回歸，因此被用(yòng)來(lái)交易。交易的(de)規則就是經典的(de)統計套利，當價差的(de)取值較曆史均值偏離兩個(gè)标準差時(shí)，就進行做(zuò)多(duō)或者做(zuò)空價差的(de)操作。下(xià)圖是 Gatev et al. (2006) 給出的(de)一個(gè)按上述方法找出的(de)股票(piào)配對(duì)交易的(de)例子。

我們使用(yòng)國内商品期貨數據簡單測試過這(zhè)種配對(duì)兒(ér)方法。結論是，它在形成期内确實能找到價格走勢非常接近的(de)商品配對(duì)兒(ér)，但是這(zhè)些商品在交易期内（即相對(duì)配對(duì)兒(ér)來(lái)說是樣本外）的(de)走勢相當不一緻。事實上，我們發現沒有任何業務層面的(de)機制來(lái)約束它們繼續一起移動，因此其價差也(yě)就根本不滿足均值回歸，上述方法在國内市場(chǎng)上的(de)有效性仍然是個(gè)大(dà)大(dà)的(de)問号。

4 配對(duì)交易的(de)不足

均值回歸策略的(de)特點是“收益有限、風險無限”。上述兩種使用(yòng)協整和(hé)價格距離構建配對(duì)交易的(de)策略在這(zhè)方面體現的(de)可(kě)謂是淋漓盡緻。

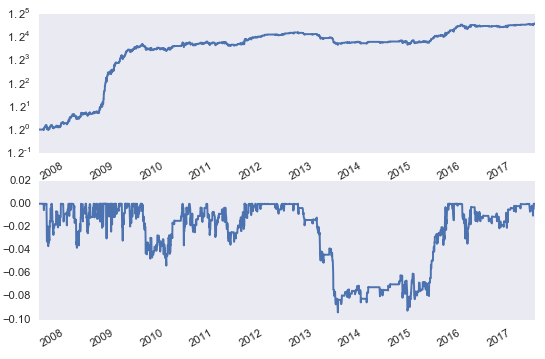
來(lái)看前半句，即便是能找到兩個(gè)靠譜的(de)投資品，使它們的(de)價差呈現穩定的(de)均值回歸特性，基于這(zhè)個(gè)價差的(de)策略的(de)交易次數也(yě)會非常少。這(zhè)是因爲隻有當價差偏離到一定的(de)程度（比如 2 個(gè)标準差之外），策略才可(kě)能進行交易，而這(zhè)種偏離發生的(de)頻(pín)率非常低。所以，這(zhè)類策略通(tōng)常在很長(cháng)時(shí)間内都沒有任何交易。下(xià)圖是利用(yòng) EWA 和(hé) EWC 這(zhè)兩個(gè) ETFs 構建的(de)配對(duì)交易（關于這(zhè)個(gè)策略的(de)更具體的(de)描述，請參考《均值回歸：循規蹈矩，偶發癫狂》）。該策略的(de)年化(huà)連續收益率爲 8.72%，最大(dà)回撤 -9.38%。從淨值和(hé)最大(dà)回撤曲線中看出很大(dà)的(de)一部分(fēn)收益來(lái)自 2009 年；在 2013 年到 2015 年間，策略發生了(le)長(cháng)達 758 個(gè)自然日的(de)回撤。

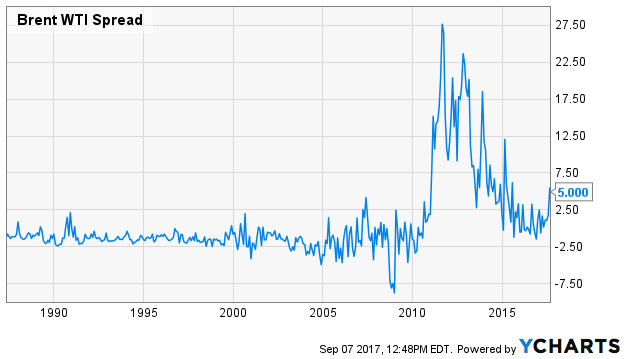
再來(lái)看看後半句。由于被用(yòng)來(lái)配對(duì)的(de)投資品之間很難滿足一價定理(lǐ)，所以沒有任何金融業務上的(de)核心邏輯來(lái)保證價差會一直滿足均值回歸。比如 Brent 和(hé) WTI 這(zhè)兩種原油，它們的(de)價格走勢應該非常接近。而這(zhè)二者的(de)價差（下(xià)圖）在 2011 年之前也(yě)确實呈現出穩定的(de)均值回歸特性。但是從 2011 年開始風雲突變，這(zhè)兩種油的(de)走勢就不再一緻，它們的(de)價差也(yě)幾乎沒有表現出任何回歸的(de)現象。不難想象一個(gè)交易該價差的(de)策略在價差突破曆史阈值之後不但沒有回歸、反而持續迅速擴大(dà)時(shí)的(de)絕望。

基于上述原因，大(dà)量的(de)實證顯示，這(zhè)類策略的(de)收益風險比較差。既然找到多(duō)個(gè)投資品并構建一個(gè)滿足均值回歸的(de)價差不是特别靠譜，那麽有沒有更好的(de)辦法呢(ne)？究其核心，構建一個(gè)均值回歸策略需要的(de)是找到一個(gè)具有負的(de)自相關性的(de)收益率序列。正是由于投資品的(de)絕對(duì)收益率幾乎是随機的(de)（沒有統計上顯著的(de)負相關性），人(rén)們才退而求其用(yòng)不同的(de)投資品構建能夠回歸的(de)價差（使價差收益率滿足負相關性）。雖然投資品的(de)絕對(duì)收益率幾乎是随機的(de)，但是在正确的(de)方法下(xià)，投資品的(de)殘差收益率是可(kě)以用(yòng)來(lái)構建均值回歸策略的(de)。這(zhè)就是均值回歸的(de)新思路。

5 因子殘差法

Yeo and Papanicolaou (2017) 提出了(le)針對(duì)投資品（這(zhè)裏特指股票(piào)）殘差收益率的(de)均值回歸策略（該研究很大(dà)程度上受到了(le) Avellaneda and Lee 2010 的(de)啓發），用(yòng)幾句話(huà)來(lái)高(gāo)度概括一下(xià)就是：

下(xià)面我們結合上述過程中涉及到的(de)量化(huà)模型來(lái)對(duì)每一步做(zuò)一個(gè)簡要介紹。首先是通(tōng)過多(duō)因子模型來(lái)求出個(gè)股的(de)殘差對(duì)數收益率（Yeo and Papanicolaou 2017 使用(yòng)了(le)統計因子，即認爲因子本身是觀測不到的(de)，而是從股票(piào)的(de)收益率中直接提取的(de) —— 比如利用(yòng)主成分(fēn)分(fēn)析這(zhè)類方法）。這(zhè)裏使用(yòng)對(duì)數收益率是爲了(le)方便之後把殘差收益率直接求和(hé)得(de)到“殘差對(duì)數價格”的(de)随機過程（下(xià)文略去“對(duì)數”二字）。假設 u_it 是個(gè)股 i 在第 t 期的(de)殘差對(duì)數收益率，将 0 到 t 期内的(de)殘差收益率加起來(lái)就得(de)到 t 時(shí)刻的(de)累積對(duì)數殘差價格：

接下(xià)來(lái)，對(duì) X_it 使用(yòng) Ornstein-Uhlenbeck (OU) 過程建模。OU 過程由 Leonard Ornstein 和(hé) George Eugene Uhlenbeck 提出，該随機過程滿足如下(xià)的(de)随機微分(fēn)方程：

其中，Θ_i，μ_i，以及 σ_i 分(fēn)别是針對(duì)個(gè)股 i 的(de)模型參數，W_i 是布朗運動。和(hé)标準的(de)布朗運動相比，這(zhè)個(gè)模型的(de)不同之處在于上式右側的(de)第一項，其中 μ_i 表示 X_it 的(de)長(cháng)均值。這(zhè)一項說明(míng)，如果 X_it 大(dà)于（小于）μ_i，那麽在下(xià)一時(shí)刻的(de)增量 dX_it 會是負的(de)（正的(de)），從而使 t + 1 時(shí)刻的(de) X_i 傾向于向均值移動，而 Θ_i 則代表像均值移動的(de)速度，因此 OU 過程滿足均值回歸特性。當然，衆多(duō)個(gè)股之中，哪些的(de)殘差價格更好的(de)滿足 OU 過程需要通(tōng)過參數估計來(lái)确定。爲此，Yeo and Papanicolaou (2017) 考慮了(le)三個(gè)要求：

滿足上述條件的(de)個(gè)股則脫穎而出，它們将被用(yòng)來(lái)構建最終的(de)投資組合。在構建投資組合時(shí)，最核心的(de)一點是：整個(gè)策略針對(duì)的(de)都是個(gè)股殘差價格的(de)均值回歸。因此，在投資組合中必須讓入選的(de)個(gè)股滿足市場(chǎng)中性，更精确地說是滿足計算(suàn)殘差收益率時(shí)使用(yòng)的(de)風格因子中性。如果無法保證這(zhè)一點，即便殘差價差回歸了(le)，但是因爲在個(gè)别因子上仍有暴露，導緻的(de)股價走勢可(kě)能仍然和(hé)策略的(de)建倉方向（多(duō)、空）不同、産生虧損。

具體的(de)，在構建最優投資組合時(shí)，Yeo and Papanicolaou (2017) 考慮了(le)如下(xià)因素，其中第一個(gè)就是因子中性（假設一共有 p 個(gè)因子），此外還(hái)要求了(le) dollar 中性（即多(duō)空對(duì)應的(de)資金量相同），以及總杠杆的(de)限制。

上面的(de)最後一條是開倉的(de)方向（多(duō)、空）。在計算(suàn)開倉信号時(shí)，Yeo and Papanicolaou (2017) 采用(yòng)了(le)傳統的(de)統計套利的(de)思路，即計算(suàn)信号 S_it：

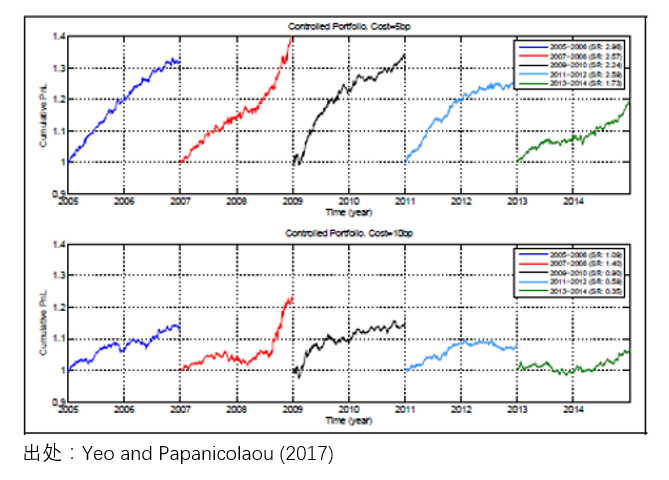
當 S_it > 1.25 時(shí)，做(zuò)空該個(gè)股，之後當 S_it 回歸到小于 0.5 時(shí)平倉；當 S_it < -1.25 時(shí)，做(zuò)多(duō)該個(gè)股，之後當 S_it 回歸到大(dà)于 -0.5 時(shí)平倉。最後來(lái)看看效果。下(xià)圖給出了(le)這(zhè)個(gè)均值回歸策略在不同時(shí)間段的(de)淨值曲線。在 5 basis points 和(hé) 10 basis points 的(de)交易成本假設下(xià)，該策略在不同的(de)時(shí)間段（包括金融危機）均取得(de)了(le)正收益，效果還(hái)是很不錯的(de)。

看到這(zhè)裏，有的(de)小夥伴也(yě)許會問，即便這(zhè)個(gè)思路确實新穎，但是實操起來(lái)似乎還(hái)有幾個(gè)問題：

不要忙著(zhe)悲觀，也(yě)許 Yeo and Papanicolaou (2017) 文中的(de)結果有一定 data mining 的(de)成分(fēn)，但是殘差價格這(zhè)背後的(de)回歸是有合理(lǐ)的(de)解釋的(de) —— 來(lái)自行爲金融學的(de)解釋。殘差收益率的(de)負相關性是由于投資者的(de)過度反應造成的(de)，而從某種意義上說，Yeo and Papanicolaou (2017) 是針對(duì)殘差收益率的(de)潛在負相關性做(zuò)了(le)更加精密的(de)定量化(huà)分(fēn)析。下(xià)面就來(lái)看看來(lái)自行爲金融學的(de)例子。

6 來(lái)自行爲金融學的(de)實證

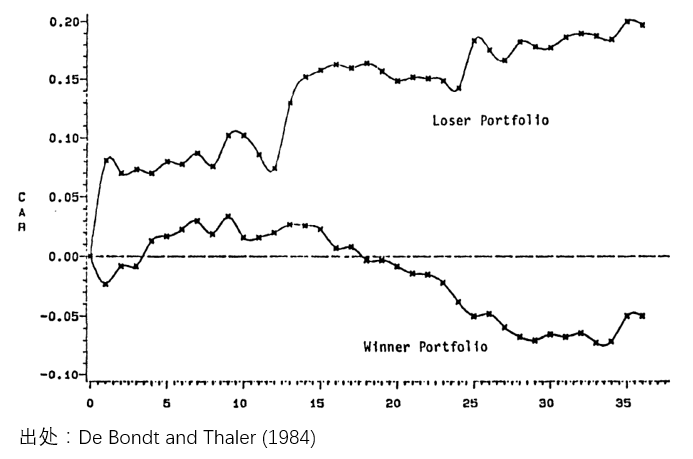
早在 1984 年，Richard Thaler（2017 年諾貝爾經濟學獲得(de)者，以研究行爲經濟學而聞名）和(hé) Werner De Bondt 寫了(le)一篇影(yǐng)響深遠(yuǎn)的(de)文章(zhāng)，題爲“Does the stock market overreact?”（De Bondt and Thaler 1984，被引用(yòng)近 8300 次）。文中，他(tā)們使用(yòng)股票(piào)相對(duì)于市場(chǎng)的(de)超額（殘差）收益率構建了(le)一個(gè)赢家組合（殘差收益率爲正）和(hé)一個(gè)輸家組合（殘差收益率爲負）。數據顯示，這(zhè)個(gè)輸家組合在未來(lái)取得(de)了(le)比赢家組合（定期調倉）更高(gāo)的(de)收益，如下(xià)圖所示。

這(zhè)個(gè)結果說明(míng)，殘差收益率确實有一定的(de)負相關性，這(zhè)造成了(le)之前跑輸市場(chǎng)的(de)組合在之後跑赢了(le)市場(chǎng)；反之亦然。這(zhè)就是爲什(shén)麽長(cháng)期來(lái)看，輸家組合遠(yuǎn)遠(yuǎn)跑赢了(le)赢家組合。在計算(suàn)殘差收益時(shí)，DeBondt and Thaler (1984) 僅僅使用(yòng)個(gè)股的(de)收益率減去市場(chǎng)的(de)收益率，并沒有考慮其他(tā)因子甚至是個(gè)股的(de) β。造成這(zhè)種現象的(de)原因正是投資者的(de)過度反應。

7 結語

一個(gè)均值回歸策略能否有效取決于它是否能夠保證價格時(shí)間序列回歸的(de)機制。大(dà)量的(de)實證顯示，純粹基于不同投資品的(de)價格數據來(lái)找這(zhè)種回歸是不太靠譜的(de)。而行爲金融學提供了(le)全新的(de)視角。流水(shuǐ)的(de)投資者，鐵打的(de)認知偏差。這(zhè)些根深蒂固的(de)認知偏差産期存在于市場(chǎng)之中，使得(de)投資品的(de)價格和(hé)收益率表現出特定的(de)性質。如果這(zhè)些行爲偏差能夠被我們所用(yòng)，從行爲金融學的(de)角度構建均值回歸策略也(yě)許會大(dà)有可(kě)爲。以某個(gè)顯著的(de)市場(chǎng)特性作爲切入點，使用(yòng)最恰當的(de)數學工具，更加精确的(de)實現一個(gè)交易目标、并獲取優秀的(de)風險收益，這(zhè)就是量化(huà)投資的(de)最大(dà)意義。

參考文獻

Avellaneda, M. and J-H. Lee (2010). Statistical arbitrage in the US equities market. Quantitative Finance 10(7), 761 – 782.

Bianchi, R., D. Michael, and R. Zhu (2009). Pairs trading profits in commodity futures markets. In: Proceedings of Asian Finance Association 2009 International Conference, June 30 – July 3, 2009, Brisbane, Queensland.

De Bondt, W. F. M. and R. Thaler (1984). Does the stock market overreact? Journal of Finance 40(3), 793 – 805.

Gatev, E., W. N. Goetzmann, and K. G. Rouwenhorst (2006). Pairs trading: Performance of a relative-value arbitrage rule. Review of Financial Studies 19(3), 797 – 827.

Yeo, J. and G. Papanicolaou (2017). Risk control of mean-reversion time in statistical arbitrage. Risk and Decision Analysis 6(4), 263 – 290.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。