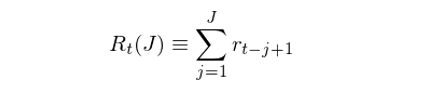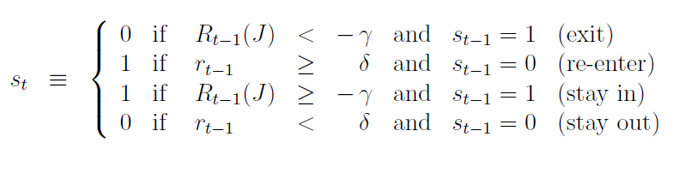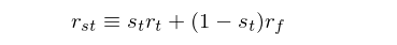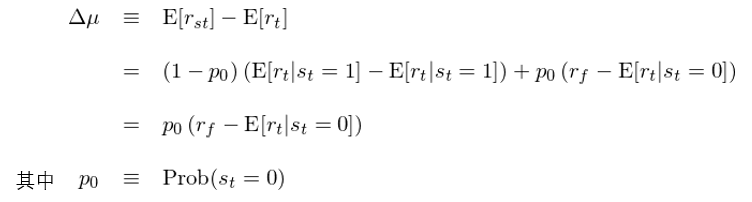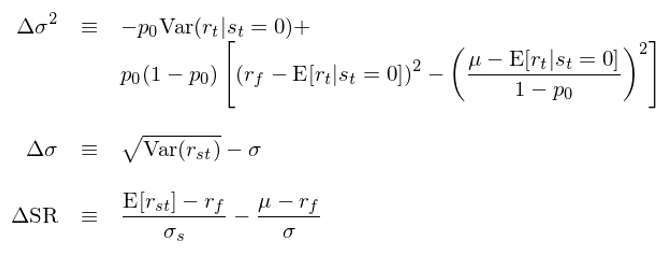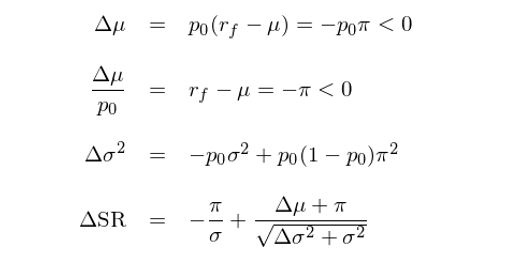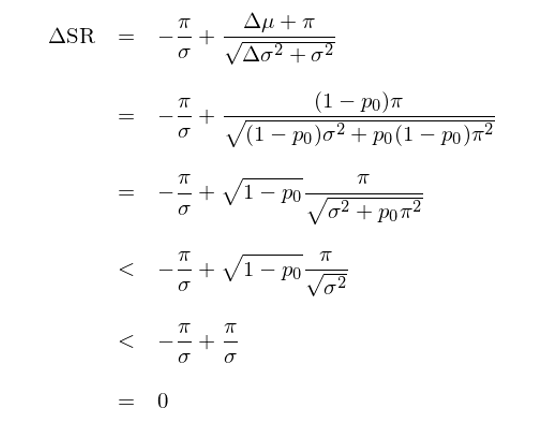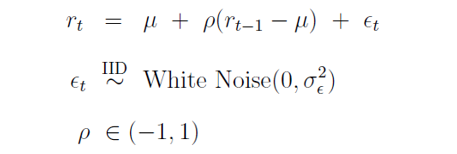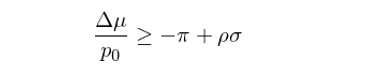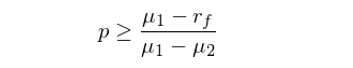止損到底有沒有用(yòng)？何時(shí)有用(yòng)？

作者：石川

摘要：一個(gè)有效的(de)策略本身是不需要額外止損的(de)。真正的(de)止損，防範的(de)是回測中沒有出現過的(de)、但在未來(lái)可(kě)能會出現的(de)未知的(de)風險。

1 引言

止損（stop loss），是當一項投資的(de)虧損達到（或超過）事先設定的(de)阈值後強制退出以避免進一步損失的(de)行爲。在二級市場(chǎng)投資中，止損是一個(gè)深入人(rén)心的(de)概念。如果問一百個(gè)交易者是否需要止損，大(dà)概能夠得(de)到 102 個(gè)肯定的(de)回答(dá) —— 一定會有人(rén)說“重要的(de)事情說三遍”。

然而，到底如何理(lǐ)解止損呢(ne)？它真的(de)有用(yòng)嗎？今天我們就定量的(de)來(lái)聊一聊止損。想要聊止損，首先必須給出明(míng)确的(de)設定，即止損發生的(de)環境。止損可(kě)以被系統地應用(yòng)于一個(gè)投資策略，成爲該策略一個(gè)必不可(kě)少的(de)組成部分(fēn)。比如技術分(fēn)析中的(de)大(dà)部分(fēn)策略，在每次建倉後，都根據價格的(de)實際走向設定跟蹤止損線，從而決定何時(shí)平倉。對(duì)于這(zhè)些策略來(lái)說，止損就是策略的(de)一個(gè)有機的(de)組成部分(fēn)。另一方面，止損也(yě)可(kě)以被施加于某個(gè)已有投資策略之外的(de)一種調控手段（因此它是一種 overlay strategy）。在這(zhè)個(gè)設定下(xià)，當已有策略出現連續虧損時(shí)，止損會強行終止該策略的(de)運行，而切換到無風險的(de)資産，直到之後某個(gè) re-enter 條件被滿足，才再次運行該策略。

在後面這(zhè)種設定下(xià)，Kaminski and Lo (2014) 針對(duì)原始策略的(de)收益率特性討(tǎo)論了(le)止損是否有效的(de)問題。本文關于止損的(de)解讀也(yě)就圍繞它來(lái)進行。下(xià)面我們将會看到，對(duì)于一個(gè)有效的(de)策略，止損是沒有任何作用(yòng)的(de)，這(zhè)和(hé)我們在《夏普率随想》中提出的(de)猜想完全一緻；但是當策略本身的(de)收益率存在一定自相關性時(shí)，止損在一定的(de)條件下(xià)是有用(yòng)的(de)；此外，在市場(chǎng)狀态發生變化(huà)時(shí)（比如牛市轉換成熊市的(de)時(shí)候），止損是有益的(de)。

2 研究框架

假設某個(gè)投資策略 P 的(de)（對(duì)數）收益率序列爲 {r_t}，該序列滿足如下(xià)兩個(gè)條件（Kaminski and Lo 2014）：

考慮上述第 2 條的(de)原因是，如果策略本身的(de)收益率還(hái)不如無風險收益率，那麽止損（即從策略切換到無風險）顯然是有益的(de)，但這(zhè)種結論沒有任何價值。因此，我們把關注點放在那些 μ 高(gāo)于 r_f 的(de)策略中。此外，定義在 t 時(shí)刻之前（包括 t）長(cháng)度爲 J 期的(de)窗(chuāng)口内，策略 P 的(de)累積（對(duì)數）收益率 R_t(J) 爲：

利用(yòng) R_t(J)，就可(kě)以定義這(zhè)個(gè)強加于策略 P 上的(de)止損規則了(le)：

這(zhè)個(gè)規則的(de)文字解釋是：如果過去 J 段時(shí)間内的(de)策略的(de)累積收益率小于阈值 -γ，則在下(xià)一時(shí)刻止損，将資金從策略 P 撤出并放到無風險資産 F 之中（exit）；如果未來(lái)某一時(shí)刻策略 P 的(de)收益率（雖然這(zhè)時(shí)資金仍投資在無風險資産 F 中，但原始策略 P 的(de)表現仍然是可(kě)以追蹤的(de)）大(dà)于給定的(de)阈值 δ 後，則在下(xià)一時(shí)刻将資金從無風險資産 F 中取出并重新投入到策略 P 中（re-enter）。當資金處在策略 P 或者無風險資産 F 時(shí)，如果止損和(hé) re-enter 的(de)條件都不觸發，則資金的(de)配置不變（stay in 或 stay out）。令 r_st 代表在 P 策略之上加入止損規則 S 後的(de)收益率，它是 r_t 和(hé) r_f 的(de)線性組合：

止損的(de)效果和(hé)規則 S 的(de)參數 γ、δ、J 以及原始策略 P 的(de)收益率序列 {r_t} 有關。爲了(le)評價止損的(de)效果，需要同時(shí)考慮收益和(hé)風險；當然更重要的(de)還(hái)是看通(tōng)過止損能否提高(gāo)收益。爲此，定義止損溢價（stopping premium）如下(xià)，它是 r_st 和(hé) r_t 的(de)期望的(de)差值：

在上面推導中的(de)第二步用(yòng)到了(le)全期望公式（Law of total expectation）。由于止損溢價中考慮了(le)止損發生的(de)概率 p_0，因此可(kě)以将它用(yòng) p_0 歸一化(huà)得(de)到 stopping ratio：Δμ/P_0，它衡量的(de)是單位時(shí)間内止損的(de)溢價；使用(yòng) Δμ/P_0 可(kě)以比較止損規則 S 的(de)不同參數 γ、δ、J。

除了(le)止損溢價之外，還(hái)可(kě)以計算(suàn)策略 P 加入止損規則 S 之後，其方差、标準差和(hé)夏普率的(de)變化(huà)（分(fēn)别記爲 Δσ^2、Δσ 和(hé) ΔSR）：

止損溢價 Δμ（或 stopping ratio）、Δσ^2（或 Δσ）以及 ΔSR 将被用(yòng)來(lái)衡量止損規則 S 是否有效的(de)改善了(le)原始策略 P 的(de)風險收益比。

3 止損對(duì)何種收益率特性有效？

下(xià)面，我們就使用(yòng)上一節定義的(de)那些指标來(lái)看看，當原始策略 P 的(de)收益率序列 {r_t} 滿足何種特性時(shí)，本文介紹的(de)這(zhè)個(gè)止損規則 S 有效。首先來(lái)看最簡單的(de)情況，即 r_t 滿足 IID。

3.1 策略 P 的(de)收益率序列滿足 IID

在《夏普率随想》中我們提出了(le)一個(gè)定義：當一個(gè)投資策略P的(de)收益率序列滿足 IID 且均值 μ 爲正時(shí)，該策略是有效的(de)。此外，針對(duì)這(zhè)個(gè)有效性的(de)定義提出了(le)一個(gè)猜想：對(duì)于一個(gè)有效的(de)策略，任何 overlay 策略都無法進一步提高(gāo)它的(de)夏普率。顯然，本文的(de)這(zhè)個(gè)止損規則就屬于一個(gè) overlay 策略。按照(zhào)上述猜想可(kě)以得(de)出一個(gè)簡單的(de)結論：對(duì)于一個(gè)有效的(de)策略（收益率序列滿足 IID），任何止損規則都無法提高(gāo)它的(de)夏普率。馬上來(lái)看看該結論是否成立。

Kaminski and Lo (2014) 指出，在 IID 這(zhè)種情況下(xià)，止損規則帶來(lái)的(de)效果爲：

Δμ < 0 說明(míng)，當 P 的(de)收益率滿足 IID 時(shí)，止損隻會降低策略的(de)收益。将 Δμ 和(hé) Δσ^2 代入到 ΔSR 的(de)表達式中并推導可(kě)得(de)：

這(zhè)個(gè)結果說明(míng)，使用(yòng)了(le)止損這(zhè)個(gè) overlay 策略之後，夏普率的(de)變化(huà) ΔSR 是小于 0 的(de)，即無法通(tōng)過止損來(lái)進一步提高(gāo)有效策略 P 的(de)夏普率。這(zhè)和(hé)上述猜想一緻。

3.2 策略 P 的(de)收益率序列滿足 AR(1) 自相關性

下(xià)面來(lái)看看複雜(zá)的(de)情況 —— P 的(de)收益率序列存在 AR(1) 自相關性。在我們的(de)頂一下(xià)，這(zhè)種策略是非有效的(de)，由于收益率之間不滿足 IID，它在時(shí)間序列上還(hái)有相關性可(kě)挖掘，以此來(lái)進一步提高(gāo)策略的(de)有效性。隻不過，本文涉及的(de)止損規則 S 僅僅是所有 overlay 策略的(de)一種，它并不一定對(duì)所有的(de)自相關性都有好的(de)效果。一個(gè) AR(1) 模型描述的(de)收益率序列滿足一下(xià)關系式，其中最重要的(de)參數是自相關系數 ρ：

當 ρ > 0 時(shí)說明(míng)收益率有正的(de)自相關性；當 ρ < 0 時(shí)說明(míng)收益率有負的(de)自相關性。當存在自相關性時(shí)，止損 S 帶來(lái)的(de) Δμ 等指标沒有簡單的(de)解析式，但 Kaminski and Lo (2014) 還(hái)是指出 Δμ/P_0 滿足如下(xià)不等式：

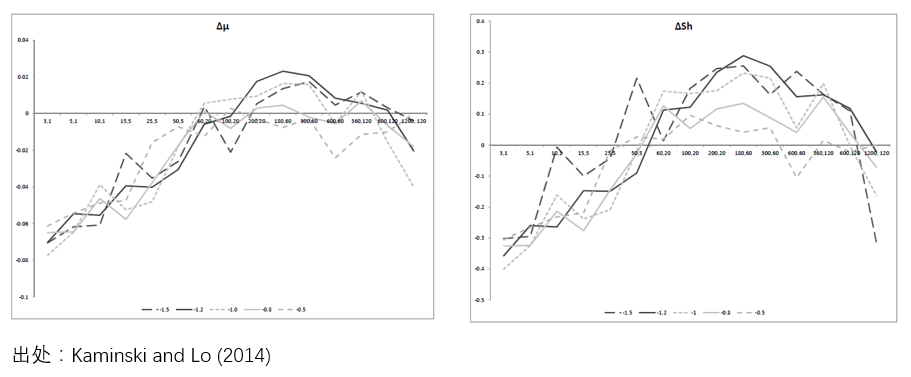
這(zhè)個(gè)關系式說明(míng)，隻有當收益率序列的(de)自相關性 ρ 不小于策略 P 的(de)夏普率時(shí)，止損溢價才大(dà)于 0。因此，對(duì)于ρ < 0 的(de)情況，止損就鐵定沒戲了(le)。這(zhè)不難理(lǐ)解。ρ < 0 說明(míng)策略本身的(de)收益率之間滿足負相關。一旦之前跌了(le)很多(duō)了(le)（以至于可(kě)以觸發止損），就往往意味著(zhe)該策略的(de)收益率要從負的(de)變成正的(de)了(le)（負相關）。如果這(zhè)時(shí)候止損，則會錯過策略的(de)反彈，因此止損造成的(de)效果爲負。而當 ρ > 0 時(shí)，如果它足夠大(dà)，那麽止損是有益的(de)。ρ > 0 以爲這(zhè)策略 P 的(de)收益率有一定的(de)趨勢。這(zhè)可(kě)能是由于策略本身是針對(duì)投資标的(de)的(de)趨勢追蹤策略，又或者是什(shén)麽高(gāo)級策略 —— 不管标的(de)有沒有優勢，該策略的(de)收益率序列都體現出了(le)趨勢。總之，一旦策略的(de)收益率有正相關性，且策略最近一直在跌，那麽正相關性說明(míng)該策略在未來(lái)可(kě)能會繼續跌；在這(zhè)種情況下(xià)，采用(yòng)止損規則切換到無風險投資品上則是有幫助的(de)。下(xià)面兩張圖來(lái)自 Kaminski and Lo (2014)。它們是針對(duì) S&P 500 的(de)期貨合約采用(yòng)不同止損參數下(xià)，止損溢價和(hé)止損帶來(lái)的(de)夏普率變化(huà)。可(kě)見，即便 S&P 500 給我們的(de)印象是随機的(de)，它也(yě)存在一定的(de)局部自相關性，而止損可(kě)以利用(yòng)它來(lái)提高(gāo)策略的(de)風險收益比。

4 止損在牛熊轉換時(shí)的(de)作用(yòng)

對(duì)于過去十年的(de) A 股來(lái)說，最簡單、有效的(de)策略無疑就是通(tōng)過趨勢追蹤抓住三波牛市，而避開對(duì)應的(de)三波熊市。換句話(huà)說，對(duì)于一個(gè)多(duō)頭策略，在熊市出現後，根據止損規則離場(chǎng)是正确的(de)選擇。如果把牛、熊市看成兩個(gè)不同的(de)市場(chǎng)狀态，那麽本文介紹的(de)數學模型是可(kě)以證明(míng)止損的(de)價值。

令 I_t = 1 表示 t 時(shí)刻市場(chǎng)處于牛市，I_t = 0 表示 t 時(shí)刻市場(chǎng)處于熊市。令 p = Prob(I_t=0|s_t=0)，即止損發生時(shí)，市場(chǎng)恰爲熊市的(de)條件概率。可(kě)以證明(míng)，隻要 p 滿足如下(xià)關系式，那麽止損就是有價值的(de)：

其中 μ_1 和(hé) μ_2 分(fēn)别爲牛、熊市時(shí)這(zhè)個(gè)持有市場(chǎng)這(zhè)個(gè)多(duō)頭策略的(de)收益率均值，并假設 μ_1 > r_f > 0 > μ_2。在牛熊轉換時(shí)，由于 μ_1 顯著大(dà)于 0 而 μ_2 顯著小于 0，因此上述關系是很容易實現的(de)，說明(míng)在熊市時(shí)，我們應該果斷止損離場(chǎng)，将資金轉移到無風險資産上。然而，與理(lǐ)論相違背的(de)是，由于各種行爲金融學的(de)認知偏差，人(rén)們在股票(piào)（或者大(dà)盤）下(xià)跌時(shí)，是很難賣出手中的(de)股票(piào)的(de)。帶著(zhe)這(zhè)個(gè)問題，下(xià)面展開我們對(duì)止損這(zhè)個(gè)行爲更深層次的(de)思考。

5 更深層次的(de)思考

作爲本文的(de)總結，我們從三個(gè)層次來(lái)思考止損的(de)作用(yòng)。首先來(lái)看看在市場(chǎng)處于下(xià)跌趨勢中，能否堅決止損對(duì)于投資者的(de)作用(yòng)。

If only I had gotten out sooner, I wouldn't have lost so much.

這(zhè)是 2008 年次貸危機之後無數投資者的(de)後見之明(míng)。但可(kě)惜，它不是先見之明(míng)，因此大(dà)量的(de)投資者虧的(de)血本無歸。從行爲金融學的(de)角度來(lái)說，人(rén)們在市場(chǎng)中表現出了(le)各種認知偏差。在面對(duì)虧損時(shí)，投資者的(de)風險偏好提升，不願意賣出已經虧損的(de)标的(de)，認爲隻要沒賣出，就沒有真的(de)虧。然而，是否賣出并不應該基于之前買入時(shí)的(de)沉沒成本，而是應該基于對(duì)于未來(lái)走勢的(de)判斷。如果未來(lái)股價會繼續下(xià)跌，那麽無論買入時(shí)的(de)成本是多(duō)少，及時(shí)止損都是正确的(de)做(zuò)法。在市場(chǎng)中，由于羊群效應的(de)存在，無論是個(gè)股還(hái)是大(dà)盤指數，它的(de)漲跌都是有趨勢的(de)。如果持有了(le)持續虧損的(de)頭寸，那麽當虧損到達阈值時(shí)，最合理(lǐ)的(de)做(zuò)法就是止損，而非繼續持有 —— 盡管止損是非常反人(rén)性的(de)。如今，數學上已經證明(míng)了(le)在這(zhè)種情況下(xià)（收益率的(de)正相關性）止損的(de)好處，就看在現實中有多(duō)少投資者能夠戰勝自己的(de)認知偏差了(le)。

在第二個(gè)層面，我們重申本文的(de)核心觀點之一：一個(gè)有效的(de)策略的(de)收益率滿足 IID，因此在這(zhè)個(gè)層面不需要 overlay 止損規則。對(duì)于一個(gè)有效的(de)（量化(huà)投資）策略，在設計它時(shí)已經考慮并充分(fēn)挖掘了(le)各種能夠利用(yòng)的(de)收益率時(shí)序相關性。因此，沒有任何 overlay 策略可(kě)以進一步提高(gāo)它的(de)夏普率。在這(zhè)樣一個(gè)策略中，策略自身當然也(yě)會做(zuò)出加倉、減倉甚至清倉的(de)操作。但是，策略的(de)減倉和(hé)清倉操作并不是傳統意義上的(de)止損 —— 策略減倉或清倉不是爲了(le)“制止虧損”，而是因爲它認爲投資标的(de)未來(lái)還(hái)會繼續跌。因此，這(zhè)樣的(de)操作屬于策略本身的(de)一部分(fēn)，而在這(zhè)種操作下(xià)策略有效（收益率滿足 IID），不需要額外的(de)止損規則。作爲挖掘策略收益率時(shí)序相關性而存在的(de)止損僅僅說明(míng)策略本身是非有效的(de)。

最後，來(lái)看看第三個(gè)層面。對(duì)于一個(gè)有效的(de)策略，止損是否一定沒有價值呢(ne)？答(dá)案也(yě)是否定的(de)。對(duì)于有效的(de)策略，止損的(de)價值在于策略之外，防止策略失效，它是作爲風控手段而存在的(de)。市場(chǎng)中從來(lái)就不缺少 unknown unknowns，因此真正的(de)止損，防範的(de)是回測中沒有出現過的(de)、但在未來(lái)可(kě)能會出現的(de)未知的(de)風險。這(zhè)才是止損的(de)最大(dà)價值。

參考文獻

Kaminski, K. M. and A. W. Lo (2014). When do stop-loss rules stop losses? Journal of Financial Markets 18(C), 234 – 254.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。