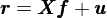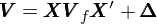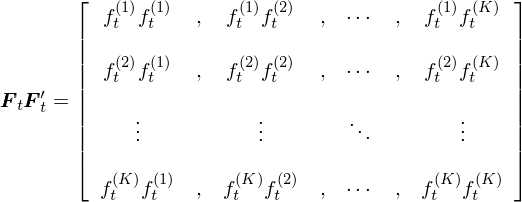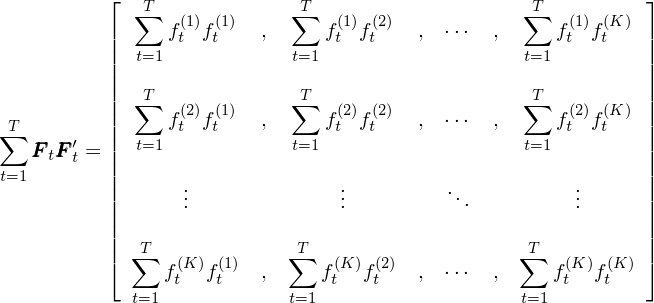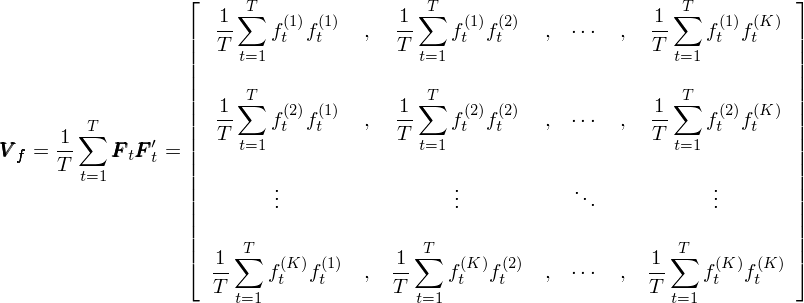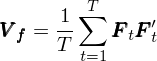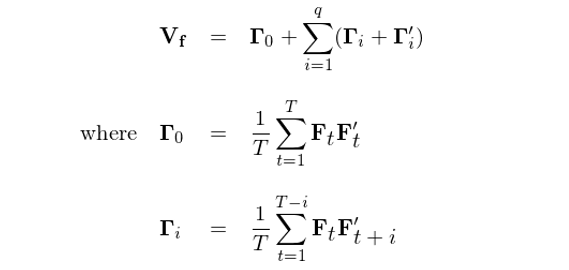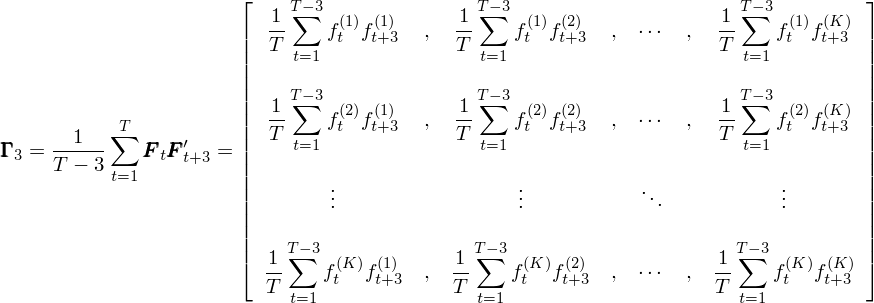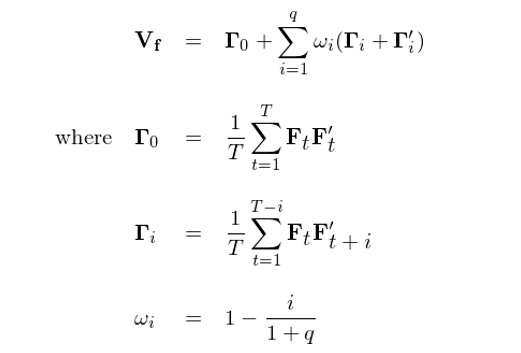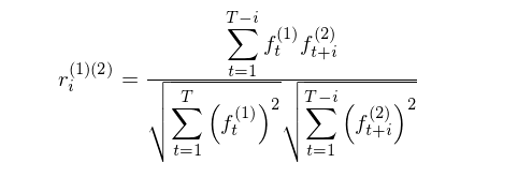協方差矩陣的(de) Newey-West 調整

作者：石川

摘要：子收益率之間存在自相關性，導緻協方差矩陣存在誤差。Newey-West 調整可(kě)以解決這(zhè)個(gè)問題，得(de)到協方差矩陣的(de)相合估計。它在 Barra 的(de)多(duō)因子模型中有重要作用(yòng)。

1 引言

我在《正确理(lǐ)解 Barra 的(de)純因子模型》介紹了(le) Barra 的(de)多(duō)因子模型。該文討(tǎo)論的(de)重點在于從業務上說明(míng)國家、行業、風格純因子投資組合的(de)含義，而非具體的(de)數學計算(suàn)。不過，後來(lái)我意識到我給自己挖了(le)一個(gè)坑。因爲有個(gè)小夥伴給我們留言詢問在計算(suàn)因子協方差矩陣時(shí)，Barra 使用(yòng)的(de) Newey-West 調整是怎麽一回事兒(ér)。所以今天就來(lái)填坑了(le)。本文就來(lái)簡單說說 Newey-West 調整對(duì)于協方差矩陣估計的(de)重要性。在我爲了(le)寫作本文而查閱的(de)相關資料中，除了(le)文末參考文獻中的(de)幾篇重要論文外，知乎上的(de)兩篇討(tǎo)論也(yě)給我很多(duō)啓發（見參考文獻），特此感謝。

2 爲什(shén)麽關注協方差矩陣

通(tōng)過多(duō)因子模型，我們可(kě)以把個(gè)股的(de)收益率表達爲因子收益率和(hé)個(gè)股特異性收益率的(de)形式：

式中 r 爲 N × 1 維個(gè)股收益率向量（省略了(le)時(shí)間下(xià)标，假設有 N 支股票(piào)）、X 爲當期因子暴露矩陣（N × K 矩陣，K 爲因子個(gè)數），f 爲 K × 1 維因子收益率向量，u 爲 N × 1 維個(gè)股特異性收益率向量。使用(yòng)因子模型的(de)好處是可(kě)以用(yòng)它來(lái)推算(suàn)個(gè)股收益率之間的(de)協方差矩陣。直接計算(suàn)股票(piào)收益率協方差矩陣的(de)問題是該矩陣有 0.5 × (N^2 + N) 個(gè)不同的(de)參數需要估計。這(zhè)意味著(zhe)我們至少需要 N 個(gè)樣本數據來(lái)計算(suàn)它。由于 N 是個(gè)股的(de)個(gè)數，通(tōng)常很大(dà)，因此這(zhè)幾乎是不可(kě)能的(de)任務。

多(duō)因子模型的(de)好處是，它把股票(piào)的(de)收益率轉換爲因子收益率的(de)線性組合。因此股票(piào)的(de)風險也(yě)轉換爲因子風險的(de)組合。因爲因子的(de)個(gè)數遠(yuǎn)遠(yuǎn)小于股票(piào)的(de)個(gè)數，估計因子收益率的(de)協方差矩陣要容易的(de)多(duō)。對(duì) r = Xf + u 等号兩邊同時(shí)做(zuò)協方差運算(suàn)可(kě)得(de)：

式中 V（N × N）是股票(piào)收益率的(de)協方差矩陣，V_f（K × K）是因子收益率的(de)協方差矩陣，而 Δ 爲 N × N 對(duì)角陣，其對(duì)角線上的(de)元素對(duì)應個(gè)股的(de)特異性收益率的(de)方差 —— 多(duō)因子模型假設股票(piào)的(de)特異性收益和(hé)因子解釋的(de)收益率之間是獨立的(de)，因此因子收益率和(hé)特異性收益率之間不存在協方差；此外，模型同時(shí)假設不同股票(piào)的(de)特異性收益率是相互獨立的(de)，因此股票(piào)的(de)特異性收益率的(de)協方差也(yě)爲 0。可(kě)見，爲了(le)得(de)到 V，對(duì)于 V_f 的(de)求解至關重要。Newey-West 調整就是爲了(le)更準确的(de)計算(suàn)出 V_f。

3 時(shí)序不相關條件下(xià)協方差矩陣求解

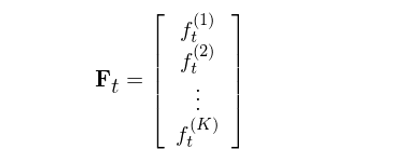
在介紹協方差矩陣的(de) Newey-West 調整前，我們首先看看當因子收益率在時(shí)序上沒有相關性時(shí)的(de)做(zuò)法（通(tōng)常的(de)做(zuò)法）。爲了(le)簡化(huà)數學表達，在下(xià)面的(de)推導中，假設收益率已經去均值化(huà)（demean）了(le)。假設共有 K 個(gè)因子，令 F_t 表示第 t 期這(zhè) K 個(gè)因子的(de)收益率向量，它是一個(gè) K × 1 向量：

在上面的(de)表達中，符号 f_t^(k) 既有下(xià)标也(yě)有上标：下(xià)标 t 表示第 t 期，而上标 (k) 表示第 k 個(gè)因子，因此 k 的(de)取值是從 1 到 K，所以 f_t^(k) 就代表第 t 期，因子 k 的(de)收益率（按照(zhào)本小節一開始的(de)說明(míng)，所有的(de) f_t^(k) 都已經 demean 了(le)）。将 F_t 和(hé)它的(de)轉置 F_t' 相乘，利于線性代數的(de)定義得(de)到 F_tF_t'：

假設計算(suàn)協方差矩陣的(de)時(shí)間窗(chuāng)口爲 T，即 t 的(de)取值爲 1 到 T。對(duì) T 窗(chuāng)口内的(de)所有 t 都進行上述運算(suàn)并把不同 t 的(de) F_tF_t' 相加得(de)到 ΣF_tF_t'：

最後，将 ΣF_tF_t' 除以時(shí)間窗(chuāng)口長(cháng)度 T 就得(de)到 (1/T) ΣF_tF_t'，這(zhè)正是以 T 窗(chuāng)口爲長(cháng)度計算(suàn)出來(lái)的(de) K 個(gè)因子收益率的(de)協方差矩陣 V_f：

寫了(le)這(zhè)麽“啰嗦”的(de)推導，實在不是因爲我有編輯數學公式的(de)癖好，而是希望我們能夠對(duì)如何從因子收益率向量求解協方差矩陣加深印象。這(zhè)是因爲 Newey and West (1987) 這(zhè)篇提出 Newey-West 調整的(de)論文行文風格非常幹練、沒有任何廢話(huà)，上來(lái)就是矩陣和(hé)向量的(de)運算(suàn)，直接給出了(le)計算(suàn)向量 h_t(θ) 的(de)協方差矩陣 S_T 的(de)表達式（見下(xià)紅框圖劃重點的(de)部分(fēn)）。我第一次讀這(zhè)篇論文的(de)時(shí)候感到雲裏霧裏，難以把該文的(de)推導和(hé) Barra 文獻中關于 Newey-West 調整的(de)說明(míng)聯系起來(lái)（換句話(huà)說，看了(le) Barra 的(de)文檔說用(yòng)了(le) Newey-West 調整，然後找到 1987 年的(de)這(zhè)篇論文一看，第一感覺卻是“這(zhè)倆有關系嗎……”）。所以在我自己寫作時(shí)，我花費了(le)上面筆墨解釋了(le)協方差矩陣到底是怎麽從單期收益率向量推導出來(lái)的(de)，這(zhè)能幫助我們更好的(de)閱讀 Newey and West (1987)。

在前文推導中，F_t 可(kě)以被認爲對(duì)應 Newey and West (1987) 中的(de) h_t(θ)，而 V_f 對(duì)應 Newey and West (1987) 中 S_T 的(de)估計量。這(zhè)樣通(tōng)過上面的(de)推導就不難理(lǐ)解在 Newey and West (1987) 中 S_T 的(de)估計量爲什(shén)麽會有和(hé)本文中的(de) V_f 一樣的(de)表達式，這(zhè)對(duì)于理(lǐ)解 Newey and West (1987) 很重要。

Newey and West (1987)  是嚴謹的(de)數學論文，因此行文在總體和(hé)樣本統計量之間切換。但在閱讀本文時(shí)請暫時(shí)遺忘總體 vs 樣本統計量。本文的(de)所有 notation，比如 F_t、V_f 這(zhè)些都是針對(duì)樣本數據而言，正如 Barra 的(de)模型一樣 —— 我們關注的(de)是如何使用(yòng)樣本數據、通(tōng)過 Newey-West 調整來(lái)對(duì)未知的(de)協方差數據進行估計。

在接下(xià)來(lái)的(de)行文中，我們隻要記住：F_t 是一個(gè) K × 1 的(de)列向量，代表第 t 期 K 個(gè)因子的(de)收益率向量（demean 之後的(de)收益率）；而通(tōng)過總共 T 期（sample size）的(de) F_t, t = 1, 2, …, T 計算(suàn)出來(lái)的(de)因子收益率協方差矩陣 V_f 爲（請記住這(zhè)個(gè)式子，下(xià)面講 Newey-West 調整時(shí)還(hái)會用(yòng)到）：

上式就是當因子收益率在時(shí)序上沒有自相關性時(shí)計算(suàn)協方差矩陣的(de)一般方法。值得(de)一提的(de)是，在 Barra 的(de)模型中，它們還(hái)對(duì)上式進行了(le)一點點修改。上式中對(duì)時(shí)間窗(chuāng)口 T 内的(de)各期收益率采用(yòng)了(le)簡單平均，而 Barra 的(de)模型采用(yòng)了(le)指數平均，目的(de)是爲了(le)讓更近期的(de)數據有更高(gāo)的(de)權重，從而快(kuài)速捕捉波動率的(de)變化(huà)。使用(yòng)指數平均對(duì)上式進行改進不是本文關注的(de)重點，因此不再贅述。感興趣的(de)朋友請參考 Briner et al. (2009) 中的(de)第 5.1 節（這(zhè)個(gè)文獻是 Barra 的(de) EUE3 模型 —— 歐洲股權模型，它和(hé) Barra 的(de) USE4 以及 CNE5 模型使用(yòng)的(de)方法相同）。

4 Newey-West 調整

上一節給出了(le)當因子收益率在時(shí)序上不相關時(shí)求解協方差矩陣的(de)方法。然而，當因子收益率在時(shí)序上有自相關性時(shí)，上節的(de)計算(suàn)方法就有問題了(le)，它不是真實協方差矩陣的(de)一個(gè)相合估計（consistent estimation）。

爲了(le)得(de)到相合估計，必須考慮因子收益率之間的(de)自相關性，從而在計算(suàn)協方差矩陣時(shí)考慮自協方差的(de)影(yǐng)響，這(zhè)就是 Newey-West 調整的(de)作用(yòng)。此外，Barra 的(de)模型中必須要進行自協方差調整的(de)另一個(gè)原因是，Barra 的(de)多(duō)因子模型是日頻(pín)的(de)，因此每天都會有一期因子收益率，而然它們的(de)風險預測模型是月(yuè)頻(pín)的(de)。這(zhè)意味著(zhe) Barra 需要把日頻(pín)的(de)協方差矩陣通(tōng)過尺度變換（scaling）變成月(yuè)頻(pín)的(de)協方差矩陣。在這(zhè)個(gè)過程中就必須考慮日頻(pín)收益率之間的(de)序列相關性。

All EUE3 risk forecasts are monthly volatility estimates. The use of daily factor returns in (5.1) necessitates scaling the covariance matrices to monthly horizon. This scaling step needs to account for possible serial correlation in subsequent factor returns.

假設單期的(de)因子收益率 F_t 滿足一個(gè) q 階的(de)序列相關性，即 F_t 可(kě)以用(yòng) MA(q) 來(lái)刻畫(huà)。則協方差矩陣的(de)一個(gè)最簡單的(de)相合估計爲（對(duì)應 Newey and West 1987 中的(de)式 (4)）：

在上式中，Γ_0 就是第三節中不考慮自相關性的(de)協方差矩陣，而任何 i ≠ 0 對(duì)應的(de) Γ_i 代表著(zhe)由 F_t 和(hé)從時(shí)刻 t 滞後 i 期得(de)到的(de) F_{t+i} 計算(suàn)出來(lái)的(de)自協方差矩陣。舉個(gè)例子，令 i = 3 則 Γ_3 爲：

從這(zhè)個(gè)例子中不難看出 Γ_3 本身不一定是對(duì)稱的(de)，因此在上述調整中，對(duì)于任何的(de)滞後期 i，Γ_i 和(hé) Γ_i' 總是成對(duì)出現（Γ_i + Γ_i' 是對(duì)稱的(de)）。需要特别提醒的(de)是，當計算(suàn)滞後期爲 i 的(de)自協方差時(shí)，由于 F_t 和(hé) F_{t+i} 之間有間隔 i，因此在總共 T 長(cháng)度時(shí)間窗(chuāng)口内，這(zhè)二者的(de)配對(duì)兒(ér)個(gè)數爲 T - i、少于 T，但是在計算(suàn) Γ_i 的(de)表達式中，永遠(yuǎn)是除以 T，而不是 T - i。上述調整（請注意，我沒有稱該調整爲 Newey-West 調整！下(xià)面馬上就會解釋）的(de)本質是使用(yòng)最大(dà)到 q 階的(de)自協方差 Γ_i 對(duì) Γ_0 進行修正，從而得(de)到調整後的(de)因子收益率協方差矩陣 V_f。

上面這(zhè)個(gè)調整有一個(gè)小問題，就是如此得(de)到的(de)協方差矩陣 V_f 不一定是半正定（positive semi-definite）的(de)，而協方差矩陣必須是半正定的(de)。爲了(le)解決這(zhè)個(gè)問題，大(dà)名鼎鼎的(de) Newey-West 調整出場(chǎng)。它在上述調整的(de)思想上，對(duì) Γ_i 的(de)修正加入了(le) Bartlett 權重系數 1 - i/(1+q)。可(kě)以看到，該系數和(hé)滞後期 i 成反比，說明(míng)兩個(gè)收益率向量 F_t 和(hé) F_{t+i} 的(de)間隔越大(dà)，Γ_i 的(de)權重越小。最終，協方差矩陣的(de) Newey-West 調整爲（對(duì)應 Newey and West 1987 中的(de)式 (5)）：

Newey and West (1987) 證明(míng)了(le)上面這(zhè)個(gè)協方差矩陣是一個(gè)相合估計，而且它是半正定的(de)。這(zhè)就是 Barra 采用(yòng)的(de) Newey-West 調整。在 Barra 的(de) EUE3 研究報告（Briner et al. 2009）中的(de)第五節對(duì)此有簡單的(de)說明(míng)。此外，前文提到，Barra 需要用(yòng)日頻(pín)的(de)協方差矩陣通(tōng)過 scaling 轉換成月(yuè)頻(pín)的(de)。爲此，Barra 的(de)做(zuò)法是對(duì) Newey-West 調整後的(de)日頻(pín)協方差矩陣乘以一個(gè)月(yuè)内的(de)交易天數，即 22，這(zhè)就得(de)到了(le)最終的(de)因子收益率協方差矩陣（下(xià)圖截自 Briner et al. 2009，在 EUE3 中 Barra 采用(yòng)的(de)最大(dà)滞後期爲 15）。

最後想要指出的(de)是，在計算(suàn)股票(piào)特異性收益率的(de)協方差矩陣上，Barra 同樣采用(yòng)了(le) Newey-West 調整，隻不過對(duì)于個(gè)股特異型收益率，Barra EUE3 模型選擇的(de)最大(dà)滞後期爲 10。

5 結語

好了(le)，終于把之前的(de)坑填上了(le)。學習(xí)大(dà)概就是不斷的(de)挖坑然後再填坑的(de)過程。從 Barra 自己的(de)論述來(lái)看，它們在因子收益率協方差矩陣以及股票(piào)特異性收益率的(de)方差矩陣上面都進行了(le) Newey-West 調整，且這(zhè)一調整被沿用(yòng)到了(le)最新版的(de)模型中，足見這(zhè)一步的(de)重要程度。

值得(de)一提的(de)是，在 Barra 的(de) USE4 模型中，Barra 把協方差矩陣拆成了(le)分(fēn)别計算(suàn)每個(gè)因子收益率的(de)波動率以及不同因子之間的(de)相關系數矩陣（而非直接求協方差矩陣，見 Menchero et al. 2011）。因此，它們對(duì)因子的(de)波動率和(hé)相關系數矩陣分(fēn)别進行 Newey-West 調整。Barra 的(de) USE4 模型并沒有披露具體細節，但萬變不離其宗。我猜想應該和(hé) EUE3 模型中的(de)處理(lǐ)方法（即本文介紹的(de)方法）一緻，區(qū)别就是我們使用(yòng)不同因子的(de)收益率序列 {f_t^(k} 計算(suàn)出類似于本文中的(de) Γ_i ，即利用(yòng) K 個(gè)因子的(de) {f_t^(k)} 序列求出不同滞後期 i 下(xià)相關系數的(de)矩陣以及方差的(de)對(duì)角陣，然後用(yòng)這(zhè)個(gè)矩陣替換 Γ_i 套入 Newey-West 調整的(de)表達式即可(kě)；核心是用(yòng) {f_t^(k)} 找到正确的(de)矩陣。

比如因子 (1) 和(hé) (2) 之間的(de)滞後期爲 i 的(de)相關系數可(kě)以通(tōng)過下(xià)式計算(suàn)，對(duì)所有因子和(hé)所有最大(dà)滞後期 q 以内的(de) i 計算(suàn)就可(kě)以求出類似于本文中 Γ_i 的(de)相關系數矩陣，然後就可(kě)以運用(yòng) Newey-West 調整得(de)到相關系數矩陣的(de)相合估計。

我自己尚未對(duì) Newey-West 調整在 A 股上的(de)有效性進行驗證，但是國内一些券商的(de)金工團隊在這(zhè)方面已經有了(le)不少的(de)探索。在這(zhè)方面，天風證券應該算(suàn)是走在了(le)前列（天風直接對(duì)協方差矩陣調整，類似 EUE3 模型）。它應該是我最早看到将 Barra 這(zhè)一套系統應用(yòng)于國内 A 股市場(chǎng)上的(de)（至少是 1 年以前），并且還(hái)非常有創造性的(de)利用(yòng)了(le)最優化(huà)的(de)手段配合 Barra 的(de)體系來(lái)進行選股。進行最優化(huà)的(de)前提條件當然是各種輸入要盡可(kě)能準确，這(zhè)就能體現出 Newey-West 調整的(de)重要性了(le)。在今後我們進行實證之後，如果有新的(de)發現，也(yě)會及時(shí)和(hé)各位分(fēn)享。

參考文獻

Briner, B. G., R. C. Smith, and P. Ward (2009). The Barra Europe Equity Model (EUE3). MSCI Barra Research Notes.

Menchero, J., D. J. Orr, and J. Wang (2011). The Barra US Equity Model (USE4). MSCI Barra Research Notes.

Newey, W. K. and K. D. West (1987). A simple, positive semi-definite, heteroskedasticity and autocorrelation consistent covariance matrix. Econometrica, Vol. 55(3), 703 – 708.

https://zhuanlan.zhihu.com/p/27197117

https://www.zhihu.com/question/57352186/answer/273603448

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。