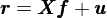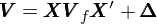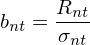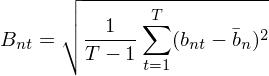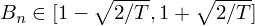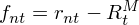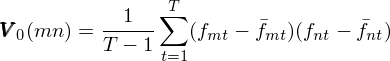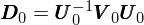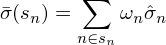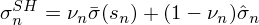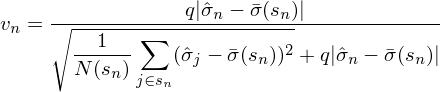Barra 因子模型中的(de)風險調整

作者：石川

摘要：除了(le) Newey-West 調整，Barra 模型中同時(shí)還(hái)使用(yòng)了(le) Eigenfactor 風險調整和(hé)貝葉斯收縮來(lái)進一步提高(gāo)協方差矩陣的(de)估計。本文介紹這(zhè)兩種技巧。

1 引言

本文介紹一下(xià) Barra 模型中關于風險的(de)兩處調整，它們都是 Barra 模型中的(de)核心組成部分(fēn)。在《正确理(lǐ)解 Barra 的(de)純因子模型》中曾經提到，Barra 的(de)純因子模型沒有什(shén)麽可(kě)投資性，但是它仍然有兩個(gè)重要的(de)作用(yòng)：

通(tōng)過多(duō)因子模型，股票(piào)的(de)超額收益被分(fēn)解爲被因子解釋的(de)部分(fēn)以及各自的(de)特異性收益率：

在上式中 r 爲 N × 1 維個(gè)股收益率向量（省略了(le)時(shí)間下(xià)标，假設有 N 支股票(piào)）、X 爲當期因子暴露矩陣（N × K 矩陣，K 爲因子個(gè)數），f 爲 K × 1 維因子收益率向量，u 爲 N × 1 維個(gè)股特異性收益率向量。通(tōng)過因子模型可(kě)知，個(gè)股收益率的(de)協方差滿足如下(xià)關系：

其中 V（N × N）是股票(piào)收益率的(de)協方差矩陣，V_f（K × K）是因子收益率的(de)協方差矩陣，而 Δ 爲 N × N 對(duì)角陣，其對(duì)角線上的(de)元素對(duì)應個(gè)股的(de)特異性收益率的(de)方差。 爲了(le)得(de)到 V 的(de)準确估計，對(duì)于 V_f 和(hé) Δ 的(de)求解至關重要。在上一期《協方差矩陣的(de) Newey-West 調整》中，我們指出爲了(le)得(de)到更準确的(de)估計，Barra 對(duì) V_f 和(hé) Δ 都進行了(le) Newey-West 調整。然而，Barra 對(duì)風險調整的(de)腳步并沒有止步于此。在 Newey-West 調整之後，它們對(duì)因子收益率的(de)協方差矩陣 V_f 進行了(le) Eigenfactor risk adjustment，并對(duì)個(gè)股的(de)特異性收益率方差矩陣 Δ 進行了(le)Bayesian shrinkage（貝葉斯收縮）。本文就來(lái)對(duì)它們分(fēn)别做(zuò)簡要介紹。在此之前，先讓我們了(le)解另外一個(gè)概念：Bias statistic（偏差統計量），這(zhè)是因爲本文關注的(de)兩種調整都是以降低 Bias statistic 爲目标的(de)。

2 偏差統計量

Bias statistic 是評估風險模型準确性的(de)一個(gè)常用(yòng)指标（Menchero et al. 2011），它用(yòng)來(lái)衡量風險預測值和(hé)風險實際值（用(yòng)已實現波動率來(lái)評估）之間的(de)誤差。如果這(zhè)二者之間有顯著誤差，則我們說這(zhè)個(gè)風險預測是有偏的(de)，故這(zhè)個(gè)統計量稱爲偏差統計量。在數學上，偏差統計量的(de)定義如下(xià)。令 R_{nt} 爲某投資組合 n 在 t 期的(de)收益率，σ_{nt} 是 t 期期初（beginning-of-period）的(de)預測風險。用(yòng) σ_{nt} 對(duì) R_{n_t} 進行标準化(huà)得(de)到：

上面這(zhè)個(gè)标準化(huà)在數學上的(de)含義是将 R_{nt} 的(de)波動率 —— 實際的(de)已實現波動率 —— 使用(yòng)期初預測的(de)波動率 σ_{nt} 進行标準化(huà)。如果期初風險預測是準确的(de)，那麽 b_{nt} 的(de)标準差應該爲 1。利用(yòng)總共 T 期的(de) b_{nt} 計算(suàn)樣本标準差就得(de)到 Barra 定義的(de)偏差統計量 B_n：

在收益率符合正态分(fēn)布的(de)假設下(xià)，B_n 的(de) 95% 的(de)置信區(qū)間爲：

可(kě)見，當樣本個(gè)數足夠大(dà)（即 T 足夠大(dà)）的(de)時(shí)候，偏差統計量 B_n 應該離 1 不遠(yuǎn)。如果它離 1 不遠(yuǎn)則說明(míng)我們在期初的(de)風險預測值比較準确，反之則意味著(zhe)期初的(de)風險預測值是有偏的(de)，這(zhè)時(shí)就需要修正。在上面的(de)使用(yòng)中，一個(gè)比較強的(de)假設是收益率滿足正态分(fēn)布。當背離這(zhè)條假設時(shí)，B_n 很有可(kě)能遠(yuǎn)離 1 而這(zhè)卻并不意味著(zhe)風險的(de)預測是有偏的(de)。在這(zhè)方面，Barra 的(de) USE4 research note （Menchero et al. 2011）裏面有更多(duō)的(de)討(tǎo)論。在本文的(de)最後，我們簡單評論一下(xià)這(zhè)個(gè)正态分(fēn)布假設。好了(le)，現在我們清楚了(le)偏差統計量，馬上來(lái)看對(duì)協方差矩陣的(de) eigenfactor 風險調整。

3 協方差矩陣的(de) Eigenfactor 風險調整

Barra 的(de) USE4 模型中，在對(duì)因子收益率協方差矩陣進行 Newey-West 調整之後，又進行了(le) Eigenfactor 調整。關于這(zhè)個(gè)調整介紹的(de)最詳細的(de)文獻是 Menchero, Wang, and Orr (2011)，這(zhè)篇文章(zhāng)比 USE4 模型文檔中的(de)介紹要更完整，我們就從它講起。本節的(de)介紹偏重于解釋 Eigenfactor 調整的(de)業務意義，會涉及少量必要的(de)數學推導，但是不會詳述所有的(de)技術細節。這(zhè)裏請暫時(shí)忘記因子，因爲上面這(zhè)篇文章(zhāng)的(de)研究的(de)對(duì)象是個(gè)股超額收益的(de)的(de)協方差矩陣。超額收益是相對(duì)市場(chǎng)而言的(de)，定義如下(xià)：

上式中， r_{nt} 是股票(piào) n 在交易日 t 的(de)收益，R_t^M  是該日的(de)市場(chǎng)收益，f_{nt}  是股票(piào)在 t 的(de)超額收益。使用(yòng)不同股票(piào)的(de)超額收益序列，就能計算(suàn)出樣本協方差矩陣：

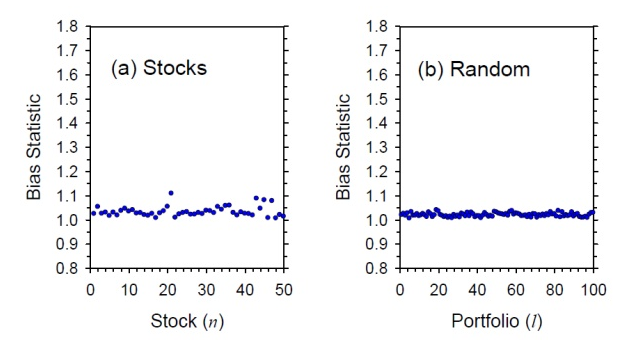
這(zhè)裏 V_0 是協方差矩陣，而  V_0(mn) 代表這(zhè)個(gè)矩陣中對(duì)應的(de)股票(piào) m 和(hé) n 之間的(de)協方差。V_0 是樣本協方差矩陣，它隻是未知總體的(de)估計，它是無偏估計嗎？是否會在某些特定使用(yòng)方法下(xià)有很大(dà)的(de)偏差？這(zhè)就是 Barra 關心的(de)。爲此采用(yòng)第二節提到的(de) Bias statistic 來(lái)評估它是否是無偏的(de)。他(tā)們首先檢查了(le)個(gè)股和(hé)随機選擇個(gè)股權重而構建的(de)投資組合，發現在這(zhè)兩種情況下(xià)，Bias statistic 都離 1 不遠(yuǎn) —— very nice。

然而在現實中，我們并不是随機的(de)投資個(gè)股，所以上面的(de)結論雖然不錯但可(kě)惜是不夠的(de)。現實中我們通(tōng)常以某種目标來(lái)優化(huà)投資組合、确定股票(piào)在組合中的(de)權重；比如使用(yòng)馬科維茨 mean-variance optimization 框架得(de)到的(de)最優組合。對(duì)于這(zhè)些最優化(huà)得(de)到的(de)投資組合，它們的(de) Bias statistic 怎樣呢(ne)？爲了(le)回答(dá)這(zhè)個(gè)問題，Eigenfactor 閃亮登場(chǎng)。假設樣本協方差矩陣 V_0 是滿秩的(de)。使用(yòng)它的(de)所有特征向量構建一個(gè)矩陣 U_0 —— 這(zhè)個(gè)矩陣的(de)每一列就是 V_0 的(de)一個(gè)特征向量。利用(yòng)線性代數的(de)性質，我們可(kě)以用(yòng) U_0 把 V_0 “旋轉”一下(xià)，變成一個(gè)對(duì)角陣：

這(zhè)個(gè) D_0 是個(gè)對(duì)角陣，它對(duì)角線上的(de)元素爲和(hé)那些特征向量對(duì)應的(de)特征值。這(zhè)其實是對(duì) V_0 進行特征分(fēn)解。這(zhè)個(gè)變換的(de)業務含義是什(shén)麽呢(ne)？假設一共有 N 個(gè)股票(piào)，則每一個(gè)特征向量都是一個(gè) N × 1 的(de)向量，它裏面第 n 個(gè)數就代表這(zhè)第 n 支股票(piào)的(de)權重。以該特征向量中的(de)數值作爲權重就得(de)到了(le)一個(gè) eigenfactor portfolio（eigenfactor 一詞是 Barra 發明(míng)的(de)，因爲來(lái)自特征向量 eigenvector）。由于一共有 N 個(gè)特征向量，所以有 N 個(gè) eigenfactor portfolios。更重要的(de)是，這(zhè)些投資組合之間相互獨立，協方差爲 0，這(zhè)在數學上體現在 D_0 是個(gè)對(duì)角陣。前面剛說過，它對(duì)角線上的(de)元素是 V_0 的(de)特征值，而它們也(yě)是這(zhè)些 eigenfactor portfolios 的(de)方差。

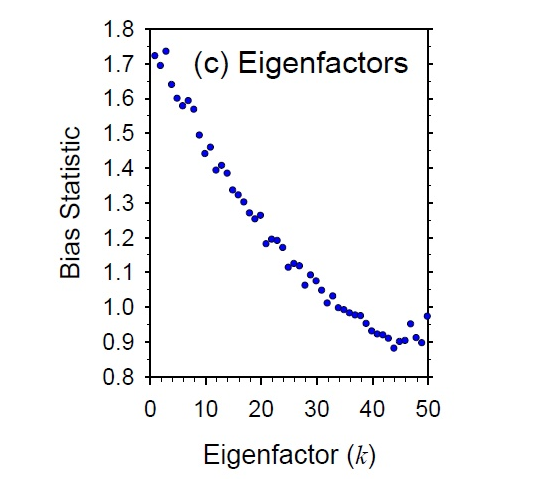
那麽這(zhè)些 eigenfactor portfolios 的(de) Bias statistics 如何呢(ne)？是否接近 1 呢(ne)？很不幸，答(dá)案是否定的(de)。下(xià)圖是按照(zhào) eigenfactor portfolios 的(de)樣本方差從小到大(dà)順序将這(zhè)些組合排列（橫坐(zuò)标），然後查看它們的(de) Bias statistics（縱坐(zuò)标）。可(kě)見，這(zhè)二者基本成反比 —— 當 eigenfactor 組合的(de)樣本方差小時(shí)，它的(de) Bias statistics 非常大(dà)，說明(míng)估計值非常不準。

即便如此我們仍然會問 —— 這(zhè) eigenfactor portfolios 在實際中有含義嗎？如果我們不按照(zhào)特征向量中的(de)權重來(lái)構建投資組合，那麽即便它們的(de) Bias statistics 偏離 1 對(duì)我們也(yě)沒有影(yǐng)響。不幸的(de)是，它們有含義！這(zhè)就是 Barra 考慮 eigenfactor 調整的(de)原因。以下(xià)是 Barra 的(de)原文：

Eigenfactors are not economically intuitive. However, they do play an important role in portfolio optimization. For instance, the first eigenfactor solves for the minimum variance portfolio subject to the constraint that the sum of squared weights adds up to 1. Similarly, the last eigenfactor solves the corresponding maximum variance problem.

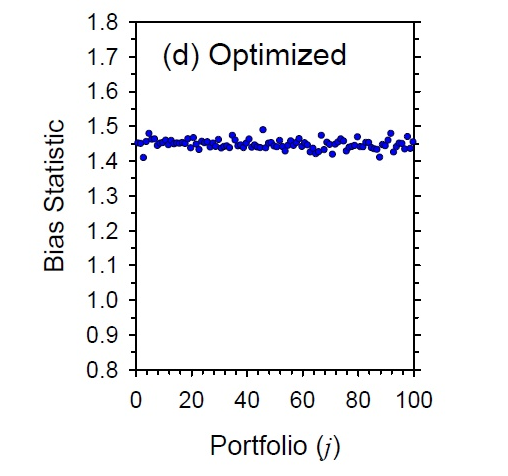
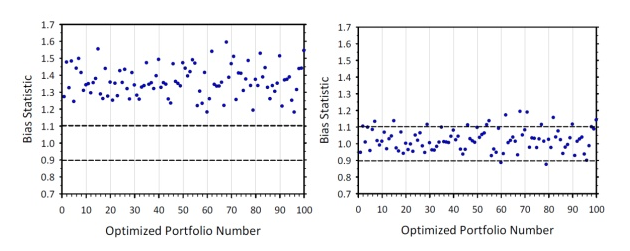
它的(de)意思是 eigenfactor portfolios 在投資組合的(de)最優化(huà)構建中有很大(dà)的(de)意義。比如，方差最小的(de) eigenfactor 組合就等價于我們以最小化(huà)組合方差爲優化(huà)目标構建的(de)組合（這(zhè)句話(huà)邏輯真完美(měi)……）；方差最大(dà)的(de) eigenfactor 組合就等價于我們以最大(dà)化(huà)方差爲優化(huà)目标（不确定是否有人(rén)這(zhè)麽幹……）而構建的(de)投資組合。在 Barra 看來(lái)，eigenfactor portfolios 和(hé)我們最終使用(yòng)這(zhè)些個(gè)股、以某種最優化(huà)目标來(lái)構建的(de)最優投資組合有著(zhe)千絲萬縷的(de)聯系。因此，如果這(zhè)些 eigenfactor portfolios 的(de) Bias statistics 很差，那麽我們可(kě)以預期，以某種目标最優化(huà)得(de)到的(de)投資組合的(de) Bias statistics 也(yě)好不到哪去（下(xià)圖是 Barra 給的(de)模拟産生的(de)最優化(huà)組合的(de) Bias statistics 例子，都高(gāo)達 1.4 以上）。

這(zhè)就是爲什(shén)麽要對(duì)協方差矩陣進行 eigenfactor 調整。讀到這(zhè)裏，細心的(de)小夥伴可(kě)能會說“你上面這(zhè)都是個(gè)股協方差矩陣啊，但是 USE4 裏面是因子協方差矩陣”。對(duì)因子協方差矩陣的(de) eigenfactor 調整的(de)數學方法和(hé)上面完全一緻。在 Menchero, Wang, and Orr (2011) 這(zhè)篇文章(zhāng)的(de)數學推導中，Barra 就說了(le)計算(suàn)樣本協方差矩陣的(de)“assets”可(kě)以是 factors，大(dà)類資産以及個(gè)股：

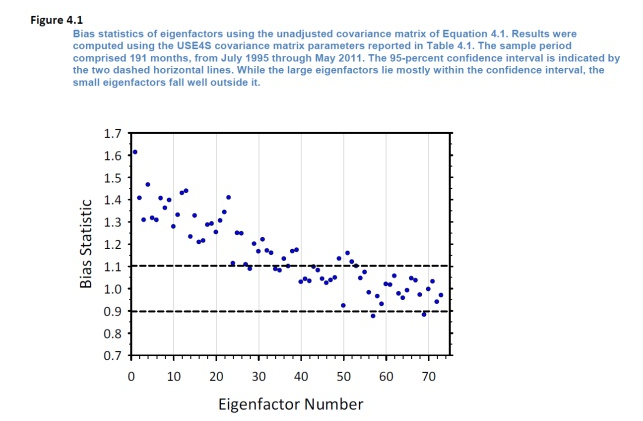
因此從數學上來(lái)說，不管上面是個(gè)股協方差矩陣還(hái)是因子協方差矩陣，都沒問題。從業務上來(lái)說呢(ne)，同樣對(duì)因子協方差矩陣做(zuò)“旋轉”。假設有 K 個(gè)因子（别忘了(le)，這(zhè)每一個(gè)因子代表著(zhe)一個(gè)由個(gè)股構建出來(lái)的(de)純因子投資組合），因此得(de)到 K 個(gè)特征向量。以特征向量爲權重得(de)到的(de) eigenfactor portfolios 恰好就是 K 個(gè)純因子投資組合的(de)某種配置組合（組合的(de)組合）。這(zhè)句話(huà)本身就足以說明(míng) eigenfactor 風險調整的(de)重要性了(le)。我們分(fēn)析因子的(de)目的(de)是爲了(le)針對(duì)這(zhè)些純因子組合的(de)風險收益特性進行進一步優化(huà)，從而把這(zhè)些因子組合放在一起，得(de)到一個(gè)多(duō)因子組合（即讓我們最終的(de)投資組合暴露于多(duō)個(gè)優異的(de) α 因子中）。然而，上面的(de)分(fēn)析指出，以純因子組合爲輸入經過優化(huà)後得(de)到的(de)投資組合，它的(de)風險估計是有偏的(de)（Bias statistic 顯著不爲 1，見下(xià)圖）。

因此，對(duì)因子的(de)協方差矩陣做(zuò) eigenfactor risk 調整也(yě)是十分(fēn)必要的(de)。這(zhè)就是 Barra 采取這(zhè)個(gè)調整的(de)原因。下(xià)圖比較了(le)調整前（左圖）後（右圖）的(de) Bias statistics，效果顯著：

上面從業務邏輯的(de)角度解釋了(le)爲什(shén)麽 Barra 要對(duì)因子協方差矩陣進行 eigenfactor risk 調整。在調整的(de)具體的(de)數學細節上面，其思想是 Bootstrap，請閱讀 Menchero, Wang, and Orr (2011) 或者是 USE4 模型的(de)文檔，這(zhè)裏就不贅述了(le)。不熟悉 Bootstrap 思想的(de)小夥伴請參考《用(yòng) Bootstrap 進行參數估計大(dà)有可(kě)爲》。

4 特質性收益率的(de)風險調整

本節來(lái)解釋 Barra 對(duì)個(gè)股特異性收益率的(de)風險調整 —— 貝葉斯收縮。貝葉斯收縮是一個(gè)常見的(de)将先驗和(hé)樣本估計結合起來(lái)的(de)手段；它是先驗和(hé)樣本估計量的(de)線性組合（見《收益率預測的(de)貝葉斯收縮》）。對(duì)（協）方差矩陣進行貝葉斯收縮并不是 Barra 的(de)獨創，事實上 Ledoit and Wolf (2003) 就提出了(le)這(zhè)個(gè)思想，并取得(de)了(le)不錯的(de)效果。他(tā)們的(de)方法也(yě)比下(xià)面要介紹的(de) Barra 的(de)收縮方法（主要是在收縮強度系數的(de)選取上）複雜(zá)的(de)多(duō)，這(zhè)個(gè)咱們以後再說。

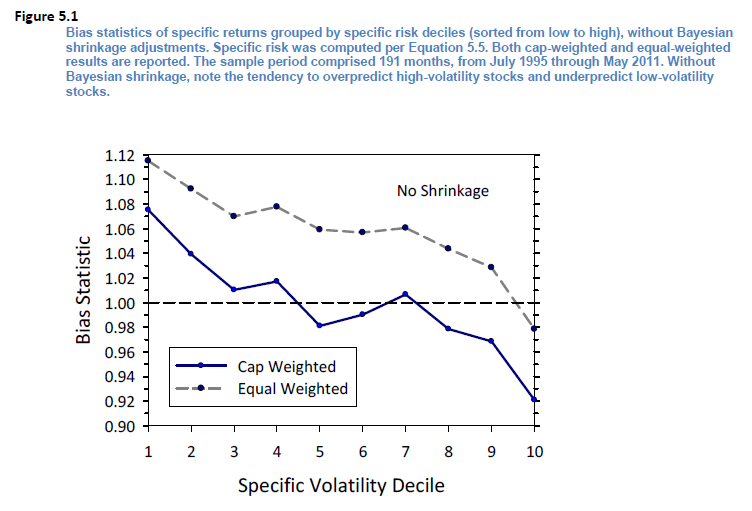
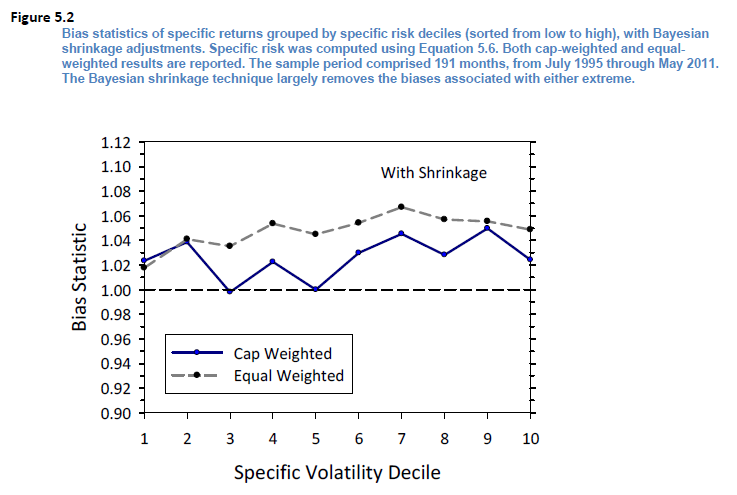
來(lái)看 Barra 的(de)問題。首先計算(suàn)出個(gè)股的(de)特異性波動率，這(zhè)是樣本估計量。但是，Barra 指出使用(yòng)樣本内數據計算(suàn)出的(de)特異性波動率在樣本外的(de)持續性很差。下(xià)圖中，所有股票(piào)按照(zhào)特異性波動率大(dà)小分(fēn)成 10 檔（圖中第 1 檔代表波動率最小；第 10 檔代表波動率最大(dà)），計算(suàn)每檔的(de)平均 Bias statistic。可(kě)以看到，對(duì)于波動率小的(de)檔，Bias statistic 顯著大(dà)于 1，說明(míng)它低估了(le)樣本外這(zhè)些股票(piào)的(de)特異性波動率；而對(duì)于波動率大(dà)的(de)檔，Bias statistic 顯著小于 1，說明(míng)它高(gāo)估了(le)這(zhè)些股票(piào)在樣本外的(de)特異性波動率。

既然使用(yòng)樣本數據估計的(de)不準，那就需要使用(yòng)先驗來(lái)矯正一下(xià)。先驗就是我們認爲正确的(de)特異性波動率，所以我們把樣本數據計算(suàn)出來(lái)的(de)特異性波動率向著(zhe)先驗來(lái)靠攏，這(zhè)就是“收縮”一詞的(de)意思，這(zhè)就是爲什(shén)麽這(zhè)個(gè)技術較貝葉斯收縮。如何計算(suàn)先驗呢(ne)？對(duì)于任意給定的(de)個(gè)股，Barra 采用(yòng)一大(dà)堆個(gè)股特異性收益的(de)波動率的(de)均值作爲先驗。這(zhè)個(gè)“一大(dà)堆”是什(shén)麽呢(ne)？Barra 把所有個(gè)股按照(zhào)市值分(fēn)成十檔，然後找到我們目标個(gè)股所在的(de)市值那一檔，而這(zhè)一檔中的(de)所有股票(piào)就是這(zhè)“一大(dà)堆”。

計算(suàn)這(zhè)一大(dà)堆中所有股票(piào)的(de)特異性波動率，取它們的(de)平均。怎麽取呢(ne)？不是簡單的(de)等權，而是按照(zhào)市值加權的(de)。這(zhè)個(gè)使用(yòng)和(hé)目标股票(piào)處在同一市值這(zhè)一檔所有股票(piào)（一大(dà)堆）按照(zhào)市值權重計算(suàn)出來(lái)的(de)特異性波動率就是先驗。以 s_n 表示市值檔位 \hat σ_n 表示 s_n 中股票(piào) n 的(de)特異性收益率，w_n 表示 s_n 中股票(piào) n 的(de)按照(zhào)其市值計算(suàn)出來(lái)的(de)權重。則這(zhè)個(gè)先驗的(de)表達式爲：

可(kě)見，先驗就是把屬于 S_n 内的(de)所有股票(piào)的(de)特異性波動率按照(zhào)它們的(de)市值爲權重平均起來(lái)。現在先驗、樣本估計量都有了(le)，最後一步就是把這(zhè)二者線性組合在一起：

上式中等式左側就是收縮後股票(piào) n 的(de)最終特異性波動率，等式右側的(de)第一項中的(de) ν_n 是在收縮時(shí)賦予先驗的(de)權重（稱爲收縮強度系數）。如何确定權重呢(ne)？它和(hé)樣本估計量與先驗的(de)偏離程度有關。具體的(de)，ν_n 的(de)表達式爲：

上式中，q 是一個(gè)經驗壓縮系數， N(s_n) 是市值檔位 s_n 中股票(piào)的(de)個(gè)數。這(zhè)個(gè)表達式中的(de)分(fēn)子以及分(fēn)母中的(de)第二項的(de) |\hat σ_n - \bar σ(s_n)| 表示了(le)我們股票(piào) n 的(de)樣本特異性波動率和(hé)其先驗之間的(de)偏離程度；而上式分(fēn)母中的(de)第一項是市值檔位 s_n 中所有股票(piào)的(de)特異性波動率和(hé)其先驗偏離程度的(de)标準差，它是這(zhè)一大(dà)堆股票(piào)的(de)平均偏離程度的(de)一個(gè)度量。最終的(de)壓縮權重 ν_n 就由這(zhè)兩個(gè)偏離程度（以及經驗系數 q）決定：

在上面 ν_n 的(de)表達式中，唯一剩下(xià)的(de)就是要确定經驗系數 q 了(le)。Barra 沒有具體說，但是不難想它一定和(hé) Bias Statistic 有關。貝葉斯收縮的(de)目的(de)就是爲了(le)降低個(gè)股特異性波動率的(de) Bias Statistic，所以可(kě)以通(tōng)過綜合考慮所有個(gè)股特異性波動率收縮前後 Bias statistic 的(de)改進來(lái)找到合适的(de) q 值。根據 USE4 文檔中報告的(de)結果，貝葉斯收縮效果顯著改善了(le)各市值檔位内個(gè)股的(de)特異性波動率（下(xià)圖）。

以上就是對(duì)特異性波動率做(zuò)的(de)貝葉斯收縮。

5 結語

本文介紹了(le) Barra 對(duì)波動率的(de)兩種調整方法，它們都是以改善 Bias statistic 爲目标。而第二節曾指出，如果收益率不滿足正态分(fēn)布，那麽 Bias statistics 可(kě)能也(yě)是不準的(de)。既然存在收益率不滿足正态分(fēn)布這(zhè)個(gè)風險，那麽 Barra 仍将上述偏差統計量用(yòng)于因子收益率協方差矩陣和(hé)個(gè)股特異性收益率方差的(de)調整中，是否合理(lǐ)呢(ne)？先來(lái)說說因子收益率。對(duì)于每個(gè)因子，它的(de)收益率是一攬子股票(piào)的(de)加權收益率（權重是從模型中根據截面回歸來(lái)的(de)），因此它是一個(gè)投資組合（純因子組合）的(de)收益率。比起個(gè)股，投資組合的(de)收益率應該更加滿足正态分(fēn)布的(de)假設。再來(lái)看看個(gè)股的(de)特異性收益率。在市場(chǎng)上流行的(de)因子模型中，對(duì)因子解釋不了(le)的(de)殘差（即特異性收益率）通(tōng)常做(zuò)的(de)假設大(dà)多(duō)是正态分(fēn)布。所以，從這(zhè)個(gè)意義上說，似乎能理(lǐ)解 Barra 堅持使用(yòng)上述偏差統計量的(de)原因。

在投資實務中，任何模型都需要假設、模型本身并無好壞。所以我們也(yě)不用(yòng)把 Barra 的(de)處理(lǐ)方法當作唯一的(de)、正确的(de)答(dá)案。這(zhè)僅僅是來(lái)自 Barra 的(de)選擇 —— 我相信這(zhè)背後自有它的(de)道理(lǐ)和(hé)考量。有的(de)小夥伴給我們留言，告訴我們國内一些券商報告中有很多(duō)其他(tā)不錯的(de)評價協方差矩陣準确性的(de)方法。那些無疑也(yě)是值得(de)我們學習(xí)和(hé)嘗試的(de)。

參考文獻

Ledoit, O. and M. Wolf (2003). Improved estimation of the covariance matrix of stock returns with an application to portfolio selection. Journal of Empirical Finance 10, 603 – 621.

Menchero, J., D. J. Orr, and J. Wang (2011). The Barra US Equity Model (USE4). MSCI Barra Research Notes.

Menchero, J., J. Wang, and D. J. Orr (2011). Eigen-adjusted Covariance Matrices. MSCI Research Insight.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。