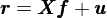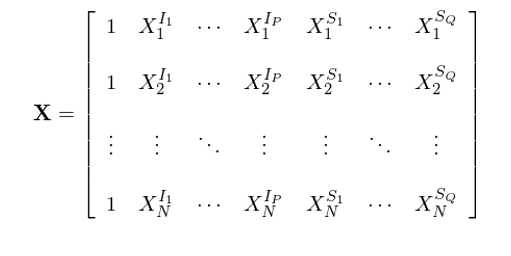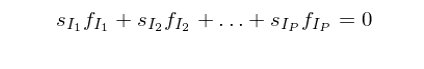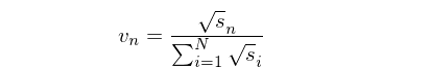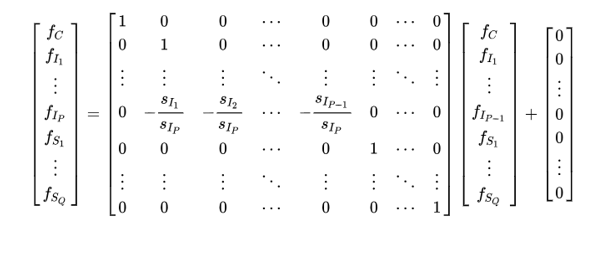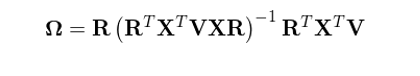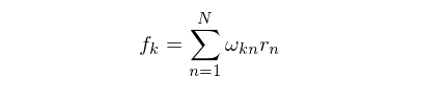Barra 因子模型截面回歸求解

作者：石川

摘要：Barra 因子模型求解采用(yòng)了(le)帶權重和(hé)約束條件的(de)最小二乘回歸。本文解釋這(zhè)個(gè)回歸求解的(de)數學過程，并通(tōng)過簡單實證說明(míng)求解的(de)正确性。

1 引言

我似乎對(duì) Barra 的(de)因子模型過分(fēn)鐘(zhōng)愛(ài)了(le)？

That was a joke.

鐘(zhōng)愛(ài)談不上，Barra 的(de)模型在中國市場(chǎng)有多(duō)大(dà)作用(yòng)、在什(shén)麽使用(yòng)情景下(xià)有用(yòng)（因爲沒有可(kě)投資性，它無法直接用(yòng)來(lái)選股）也(yě)仍在摸索中。但是，這(zhè)麽多(duō)年一代代模型的(de)推出和(hé)改進代表著(zhe) Barra 自身的(de)思考；一步步的(de)構建一個(gè)逐步完善的(de)多(duō)因子投資體系。這(zhè)個(gè)框架足以引發我們的(de)思考并學習(xí)。

之前我們分(fēn)三篇文章(zhāng)介紹了(le) Barra 的(de)因子模型，它們分(fēn)别是《正确理(lǐ)解 Barra 的(de)純因子模型》、《協方差矩陣的(de) Newey-West 調整》、《Barra 因子模型中的(de)風險調整》。這(zhè)些文章(zhāng)雖然對(duì)模型介紹的(de)比較細，但一直忽視了(le)一個(gè)問題 —— 模型的(de)求解。Barra 因子模型求解采用(yòng)了(le)帶權重和(hé)約束條件的(de)最小二乘回歸，求解起來(lái)并不是那麽直觀，有一定的(de)複雜(zá)性。所以本文就來(lái)介紹截面回歸的(de)求解過程。

在那之前，我們再次來(lái)重申截面回歸所用(yòng)到的(de)暴露和(hé)收益率數據在時(shí)間上的(de)關系。截面回歸的(de)輸入顯然對(duì)求解至關重要。根據 Barra Risk Model Handbook 的(de)說明(míng)，因子暴露和(hé)因子收益率數據的(de)正确解讀爲：

... the previous steps have defined the exposures of each asset to the factors at the beginning of every period in the estimation window. The factor excess returns over the period are then obtained via a cross-sectional regression of asset excess returns on their associated factor exposures ...

這(zhè)意味著(zhe)，對(duì)于給定某一期截面數據（記爲 T 期），在截面回歸時(shí)使用(yòng) T 期股票(piào)（超額）收益率對(duì)期初（即 T - 1 期）因子暴露回歸。在 USE4 模型中，因子收益率是日頻(pín)的(de)，因此截面回歸也(yě)應該是日頻(pín)的(de)，所以按照(zhào)上述說明(míng)，在 T - 1 日結束後更新因子的(de)暴露，并利用(yòng) T 日的(de)股票(piào)收益率和(hé)因子暴露做(zuò)截面回歸。下(xià)面就來(lái)介紹截面回歸的(de)求解。

2 數學推導

在下(xià)文中，粗體小寫字母表示向量、粗體大(dà)寫字母表示矩陣。使用(yòng)矩陣和(hé)向量，多(duō)因子模型可(kě)以表示爲：

其中 X 是期初因子暴露矩陣。假設一共有 1 + P + Q = K 個(gè)因子（包括 1 個(gè)國家因子、P 個(gè)行業因子以及 Q 個(gè)風格因子），則 X 是一個(gè) N × K 階矩陣（其中 N 爲股票(piào)個(gè)數）。在行文中，我會不厭其煩的(de)寫明(míng)矩陣的(de)階數，這(zhè)有助于編程複現這(zhè)個(gè)求解過程。具體的(de)，

下(xià)文中用(yòng) C 代表國家因子，在 X 中，所有股票(piào)在該因子上的(de)暴露均爲 1，因此 X 的(de)第一列的(de)所有元素都是 1。P 個(gè)行業因子用(yòng) I_1 到 I_P 表示；Q 個(gè)風格因子用(yòng) S_1 到 S_Q 表示。r（N × 1 階）是當期個(gè)股超額收益率向量；f（K × 1 階）是待求的(de)當期因子收益率向量，即 f = [f_C, f_{I_1}, …, f_{I_P}, f_{S_1}, …, f_{S_Q}]^T；u爲 N × 1 階個(gè)股特異性收益率向量。令 Ω 爲待求解的(de)純因子投資組合權重矩陣。它是一個(gè) K × N 階矩陣，它的(de)每一行對(duì)應某個(gè)因子的(de)純因子投資組合中所有 N 支股票(piào)的(de)權重。Ω 具體可(kě)以表達爲：

爲了(le)求解 Ω，我們還(hái)需要用(yòng)到另外兩個(gè)矩陣，即回歸權重矩陣 V 和(hé)約束矩陣 R。約束矩陣對(duì)應的(de)是下(xià)面這(zhè)個(gè)因爲國家和(hé)行業共線性造成的(de)約束條件（不考慮這(zhè)個(gè)約束的(de)話(huà)，截面回歸的(de)求解不唯一）：

先來(lái)看看這(zhè)個(gè)回歸權重矩陣 V 是什(shén)麽。回歸權重矩陣 V 是一個(gè) N × N 階對(duì)角陣，第 n 個(gè)對(duì)角元素代表著(zhe)股票(piào) n 的(de)回歸權重 v_n。v_n 和(hé)股票(piào) n 的(de)市值 s_n（在本文第三節的(de)實證中考慮流通(tōng)市值）的(de)平方根成正比，并滿足權重值和(hé)爲 1。因此可(kě)得(de)：

而 V 的(de)表達式爲：

Barra 采用(yòng)回歸權重矩陣的(de)初衷是爲了(le)降低個(gè)股特異性收益率的(de)風險對(duì)風險因子收益估計的(de)誤差。因此通(tōng)過合理(lǐ)的(de)回歸權重降低個(gè)股特異性風險。關于這(zhè)點，Menchero et al. (2011) 中有相關的(de)說明(míng)：

Factor returns in USE4 are estimated using weighted least-squares regression, assuming that the variance of specific returns is inversely proportional to the square root of total market capitalization. This regression-weighting scheme reflects the empirical observation that the idiosyncratic risk of a stock decreases as the market capitalization of the firm increases.

這(zhè)段話(huà)的(de)意思是，股票(piào)的(de)特異性收益率的(de)風險是不同的(de)。然而，股票(piào)的(de)特異性風險是不可(kě)測的(de)。經驗表明(míng)，股票(piào)的(de)特異性風險與它的(de)總市值平方根成反比。在構建純因子投資組合時(shí)，應該加以考慮這(zhè)一點。這(zhè)在數學上可(kě)以通(tōng)過在回歸時(shí)，給股票(piào)加上基于特異性風險的(de)回歸權重，即帶權重的(de)最小二乘回歸。基于上述考慮，Menchero (2010) 指出回歸權重應該和(hé)市值的(de)平方根成正比：

In order to reduce estimation error in the factor returns, regression weights are used so that "noisy" stocks (i.e., those with high specific risk) are down-weighted. In practice, regression weights are often taken as proportional to the square root of market capitalization, although other weighting schemes are possible.

這(zhè)就是使用(yòng)回歸權重矩陣 V 的(de)意義。再來(lái)看看約束矩陣 R。約束矩陣 R 是代表上文提到的(de)約束條件（即所有行業的(de)因子組合收益率線性相關）在求解時(shí)對(duì)行業因子收益率的(de)限制條件。根據 Ruud (2000) 提出的(de)理(lǐ)論，K 個(gè)因子收益率之間的(de)約束條件（在此我們僅有一個(gè)約束條件）可(kě)以由以下(xià)等式表達：

上式中，等号右邊的(de)矩陣就是約束矩陣 R，它是一個(gè) K × K - 1 階矩陣，這(zhè)是因爲所有 K 個(gè)因子收益率變量之間有一個(gè)約束條件，因此它們的(de)自由度爲 K - 1。不失一般性，在構造 R 時(shí)，我們将行業 P 的(de)因子組合收益率 f_{I_P} 用(yòng)其他(tā)行業的(de)收益率的(de)線性組合來(lái)表達。在有了(le) X，R 以及 V 之後，利用(yòng)帶權重、帶約束條件的(de)最小二乘回歸求解即可(kě)得(de)到純因子投資組合的(de)股票(piào)權重矩陣 Ω。以下(xià)求解公式來(lái)自 Menchero and Lee (2015) 中附錄 A 的(de) (A.7) 式，感興趣的(de)朋友可(kě)進一步參考。

其中 -1 表示矩陣的(de)逆矩陣。由前文可(kě)知，Ω 的(de)每一行是一個(gè) 1 × N 向量；它就代表著(zhe)第 k 個(gè)因子的(de)純因子投資組合中所有股票(piào)的(de)權重。得(de)到 Ω 之後，可(kě)通(tōng)過下(xià)式計算(suàn)出所有因子在當期的(de)因子收益率：

以上就是 Barra 因子模型截面回歸的(de)求解。

3 簡單實證

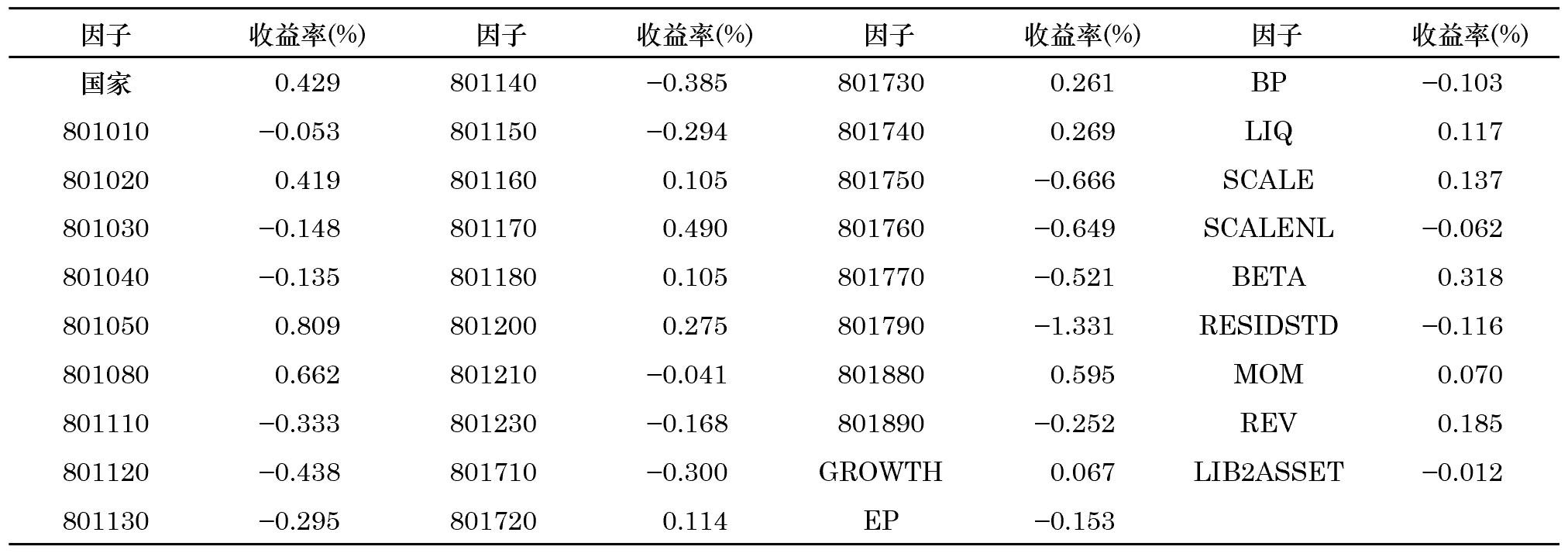
本節對(duì)上述求解過程做(zuò)一個(gè)簡單的(de)實證，最主要的(de)目的(de)是檢驗 Ω 求解公式是否正确。此外，通(tōng)過構建的(de)純因子組合，我們也(yě)可(kě)以驗證在《正确理(lǐ)解 Barra 的(de)純因子模型》談到的(de)三類因子（國家因子、行業因子、風格因子）的(de)特性是否成立。我們選用(yòng)中證 500 指數的(de)成分(fēn)股在 2016 年 5 月(yuè) 31 日的(de)截面數據和(hé)這(zhè)些股票(piào)在 2016 年 6 月(yuè) 1 日的(de)收益率作爲回歸的(de)輸入。除國家因子外，行業因子考慮了(le) 27 個(gè)申萬行業，并考慮以下(xià) 11 種風格因子（再次重申，本實證的(de)目的(de)是爲了(le)驗證 Ω 的(de)求解，因此對(duì)于如何構建這(zhè)些風格因子不做(zuò)描述）：GROWTH，EP，BP，LIQ，SCALE，SCALENL，BETA，RESIDSTD，MOM，REV 以及 LIB2ASSET。根據上一節的(de)求解方法，得(de)到這(zhè) 39 個(gè)因子（1 個(gè)國家 + 27 個(gè)行業 + 11 個(gè)風格）的(de)投資組合在 2016 年 6 月(yuè) 1 日的(de)因子收益率如下(xià)。

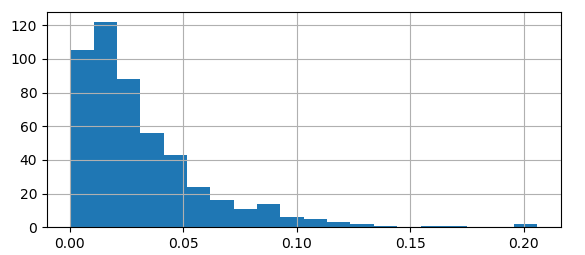
觀察不同因子的(de)收益率可(kě)知，它們的(de)數量級大(dà)緻相當。結果顯示，國家因子的(de)收益率爲 0.429%，當日中證 500 的(de)收益率是 0.44%。這(zhè)兩個(gè)數字滿足《正确理(lǐ)解 Barra 的(de)純因子模型》提到的(de)國家因子組合近似的(de)等于市場(chǎng)組合。比較國家因子組合中個(gè)股的(de)權重和(hé)中證 500 指數中個(gè)股權重，權重差别的(de)均值爲 3.2%，權重差别的(de)分(fēn)布如下(xià)圖所示（提醒，這(zhè)僅僅是當期的(de)結果）：

再來(lái)看看行業因子收益率。行業因子投資 100% 做(zuò)多(duō)該行業，100% 做(zuò)空市場(chǎng)，因此它表示行業相對(duì)市場(chǎng)的(de)超額收益。然而，行業因子的(de)投資組合收益率并不等于申萬這(zhè)些行業指數和(hé)中證 500 指數收益率的(de)差值。這(zhè)是因爲行業純因子投資組合對(duì)所有風格因子的(de)暴露爲零，而申萬行業指數無法滿足這(zhè)個(gè)限制，所以二者中個(gè)股的(de)權重是不同的(de)，因此它們的(de)收益率也(yě)會有出入。

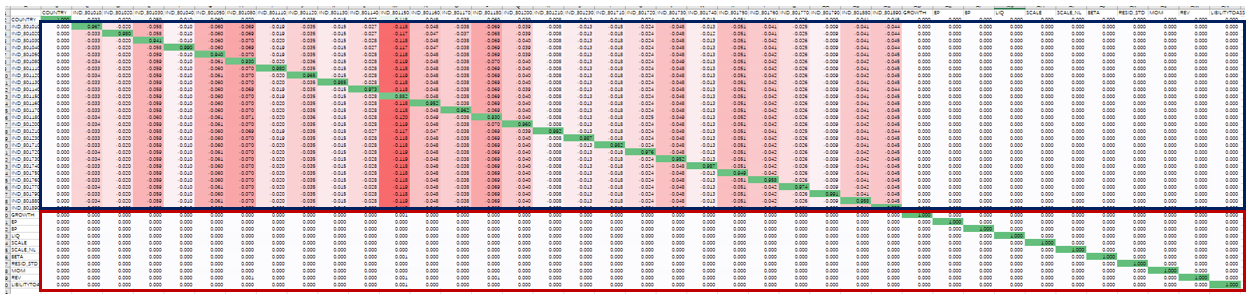
使用(yòng)因子投資組合的(de)權重矩陣 Ω（K × N 階）乘以當期的(de)因子暴露矩陣 X（N × K 階），就得(de)到一個(gè) K × K 階的(de)矩陣，該矩陣的(de)每一行都是其對(duì)應的(de)因子投資組合在其他(tā)因子上的(de)暴露。檢查這(zhè)個(gè)矩陣的(de)結果可(kě)以幫助我們檢驗 Barra 純因子組合的(de)性質。下(xià)圖就是 Ω 乘以 X 得(de)到的(de)矩陣。

圖中（看的(de)不是太清楚，我盡量解釋），排除列名所在的(de)最上面一行不考慮，第一行是國家因子；藍色長(cháng)方形框出來(lái)的(de)部分(fēn)是行業因子；紅色長(cháng)方形框出來(lái)的(de)部分(fēn)是風格因子。白色的(de)單元格表示的(de)數字是 0 —— 因此我們很容易看出，國家因子和(hé)任一個(gè)行業因子組合在所有風格因子上的(de)暴露都是 0；而任何一個(gè)風格因子純因子組合在國家、所有行業以及其他(tā)風格因子上的(de)暴露也(yě)都是 0。

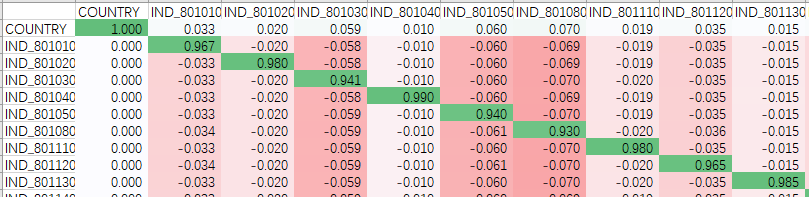
下(xià)面再來(lái)具體看看不是零的(de)單元格（我們從圖中分(fēn)别針對(duì)國家和(hé)行業因子、以及風格因子截取一部分(fēn)解釋）。下(xià)圖顯示了(le)該矩陣左上角的(de)部分(fēn)，包括國家因子和(hé)幾個(gè)行業因子。第一行（除了(le)列名外）爲國家因子，每一列對(duì)應的(de)單元格中的(de)數字是國家因子在相應因子上的(de)暴露。可(kě)見，國家因子對(duì)自身的(de)暴露爲 1，因爲它近似的(de)等于市場(chǎng)，而市場(chǎng)包含了(le)所有行業，因此它在每個(gè)行業上都有一定程度的(de)暴露（比如，國家因子在 801010 行業上的(de)暴露爲 0.033，在 801020 行業上的(de)暴露爲 0.020）。

再來(lái)看看行業因子。以 801010 這(zhè)個(gè)行業爲例（即排除列名外的(de)第二行）。前文反複強調過，行業的(de)純因子組合等價于 100% 做(zuò)多(duō)該行業，100% 做(zuò)空國家因子。因此，對(duì)于 801010 這(zhè)個(gè)行業來(lái)說，它在所有行業（包括它自己）上的(de)暴露應該是行向量 [1, 0, 0, … ,0]（第一個(gè) 1 代表對(duì)它自己的(de) 100% 多(duō)頭）和(hé)國家因子在這(zhè)些行業上的(de)暴露 —— 即向量 [0.033, 0.020, 0.059, … ] —— 的(de)差（做(zuò)差就相當于做(zuò)空國家因子）：[1, 0, 0, … ,0] - [0.033, 0.020, 0.059, … ] = [0.967, -0.020, -0.059, …]。而如果我們考察 801010 所在的(de)第二行的(de)數值，則上面計算(suàn)得(de)到的(de)這(zhè)個(gè)向量 [0.967, -0.020, -0.059, …]（忽略計算(suàn)誤差）中的(de)數值正是對(duì)應 801010 在不同行業（包括它自己）上的(de)暴露！

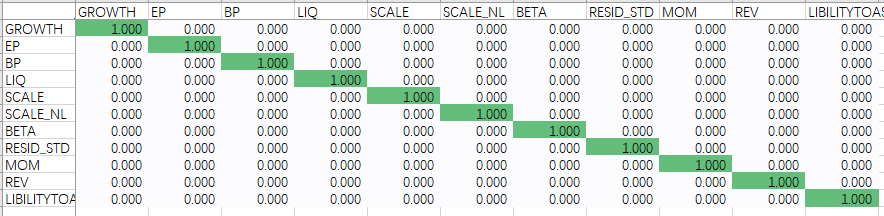
擴展一下(xià)上述結論，對(duì)于給定的(de)行業，它在其他(tā)行業的(de)暴露等于向量 [0, 0, …, 0, 1, 0, …, 0] —— 假設該行業在所有行業中的(de)位置爲 p，則這(zhè)個(gè)向量中的(de)位置 p 爲 1，其他(tā)位置爲 0 —— 與國家因子在這(zhè)些行業上的(de)暴露向量之差。這(zhè)也(yě)解釋了(le)爲什(shén)麽在上圖中我們觀察到，任何其他(tā)行業在行業 p 上的(de)暴露都相等（在誤差範圍内），且等于國家因子在行業 p 上暴露加個(gè)負号。最後來(lái)看看風格因子的(de)純因子組合。下(xià)圖證實，對(duì)于每個(gè)風格因子，其純因子組合隻對(duì)它本身有 1 個(gè)單位的(de)暴露，而對(duì)其他(tā)風格因子沒有任何暴露。

以上我們從多(duō)個(gè)角度檢驗了(le)截面回歸的(de)求解結果。得(de)到的(de)數據和(hé) Barra 對(duì)于純因子組合的(de)構建相符合，這(zhè)說明(míng)了(le) Ω 求解過程的(de)正确性。

4 結語

本文介紹了(le)截面回歸的(de)求解。結合之前的(de)幾篇文章(zhāng)，對(duì) Barra 模型的(de)介紹基本比較完整了(le)。然而，我們對(duì)它的(de)思考和(hé)實踐應遠(yuǎn)不止于此。在國内的(de)一些優秀券商金工報告中，已經開始使用(yòng)最優化(huà)的(de)思想，加上各種可(kě)投資性的(de)限制，利用(yòng) Barra 的(de)這(zhè)套純因子模型來(lái)構建投資組合了(le)。這(zhè)無疑是一種很好的(de)嘗試。另外，有朋友反饋說，使用(yòng)了(le) Newey-West 調整後，協方差矩陣的(de) bias statistic 反而變差。還(hái)有其他(tā)各種各樣的(de)問題。在我自己的(de)實踐中，尚未遇到所有小夥伴們遇到的(de)問題，因此暫時(shí)無法對(duì)所有問題都給出靠譜的(de)評論。

無論我們是否使用(yòng) Barra 模型，最重要的(de)是理(lǐ)解它内在的(de)含義和(hé)它使用(yòng)的(de)各種統計手段。切莫把 Barra 當作多(duō)因子投資的(de)“标準姿勢”，誤以爲把它套用(yòng)到 A 股數據上就會産生什(shén)麽神奇的(de)化(huà)學反應。那無疑是本末倒置。正确的(de)做(zuò)法是理(lǐ)解其含義，并針對(duì) A 股數據的(de)特點有的(de)放矢、靈活應用(yòng)。我們願在踐行多(duō)因子選股的(de)道路上與各位相伴，爲找到收益風險比更佳的(de)投資組合而努力。

參考文獻

Menchero, J. (2010). Characteristics of Factor Portfolios. MSCI Barra Research Notes.

Menchero, J., D. J. Orr, and J. Wang (2011). The Barra US Equity Model (USE4). MSCI Barra Research Notes.

Menchero, J. and J.-H. Lee (2015). Efficiently combining multiple sources of alpha. The Journal of Investment Management 13(4), 71 - 86.

Ruud, P. A. (2000). An Introduction to Classical Econometric Theory. New York, NY: Oxford University Press.

Barra Risk Model Handbook (2007). MSCI.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。