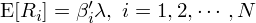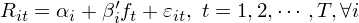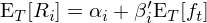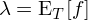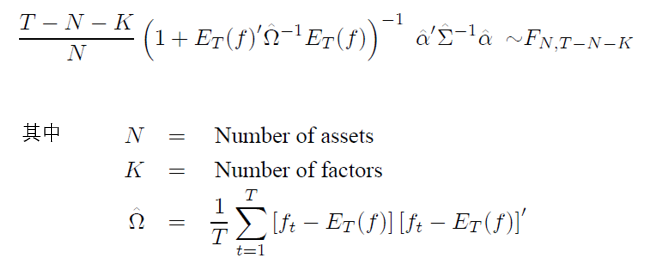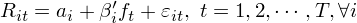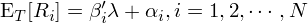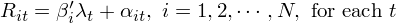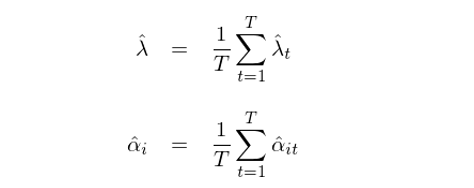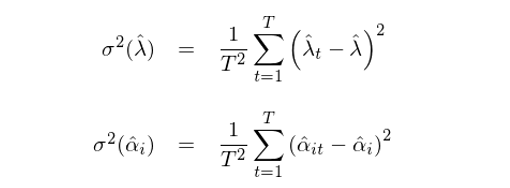股票(piào)多(duō)因子模型的(de)回歸檢驗

作者：石川

摘要：收益率均值和(hé)因子暴露在截面上的(de)關系就是多(duō)因子模型研究的(de)問題。本文討(tǎo)論一些平時(shí)在使用(yòng)多(duō)因子模型時(shí)遇到的(de)常見問題，如截面回歸 vs 時(shí)序回歸、使用(yòng) portfolio returns 和(hé)宏觀經濟指标作爲因子有什(shén)麽不同、以及因子暴露應該如何确定等。

0 引言

這(zhè)是迄今爲止我寫的(de)最重要的(de)文章(zhāng)，沒有之一。

本文的(de)題目是股票(piào)多(duō)因子模型的(de)回歸檢驗。說它重要，是因爲在多(duō)因子模型被用(yòng)于資産定價（選股）越來(lái)越普及的(de)今天，很多(duō)人(rén)不一定搞清楚了(le)多(duō)因子模型中常見的(de)時(shí)間序列回歸、截面回歸之間到底有什(shén)麽區(qū)别，以及它們在本質上又是何其相似；不一定搞清楚在使用(yòng)多(duō)因子模型給資産定價時(shí)，需要關注的(de) statistical tests 目标到底是什(shén)麽；不一定搞清楚在回歸殘差存在時(shí)序或截面相關性時(shí)，模型參數的(de) standard errors 可(kě)能完全是不準确的(de)以至于給出錯誤的(de)推斷……

本文旨在討(tǎo)論一些平時(shí)在使用(yòng)多(duō)因子模型時(shí)可(kě)能遇到的(de)各種困惑（比如什(shén)麽時(shí)候用(yòng)截面回歸、什(shén)麽時(shí)候用(yòng)時(shí)序回歸；使用(yòng) portfolio returns 作爲因子和(hé)其他(tā)比如宏觀經濟指标作爲因子有什(shén)麽不同等）。由于篇幅有限，我會把寫作重點放在對(duì)核心概念的(de)解讀上。此外，在本文中還(hái)會涉及對(duì) Barra 模型的(de)一些思考。

文章(zhāng)的(de)最後一節将會安利寫作時(shí)使用(yòng)的(de)主要參考文獻（下(xià)文中對(duì)于時(shí)序和(hé)截面回歸的(de)講解、以及對(duì) Fama-MacBeth 回歸的(de)說明(míng)來(lái)自 John Cochrane 的(de)經典教材 Asset Pricing 以及他(tā)在芝加哥(gē)大(dà)學的(de)同名網上課程的(de)相關部分(fēn)），感興趣的(de)小夥伴在閱讀本文後可(kě)以進一步參考。

1 多(duō)因子模型的(de)回歸檢驗

多(duō)因子模型是 Asset Pricing（資産定價）的(de)一種常見方法（其他(tā)的(de)方法還(hái)包括 consumption-based model 等）。一個(gè)多(duō)因子模型（假設 K 個(gè)因子）的(de)表達式如下(xià)：

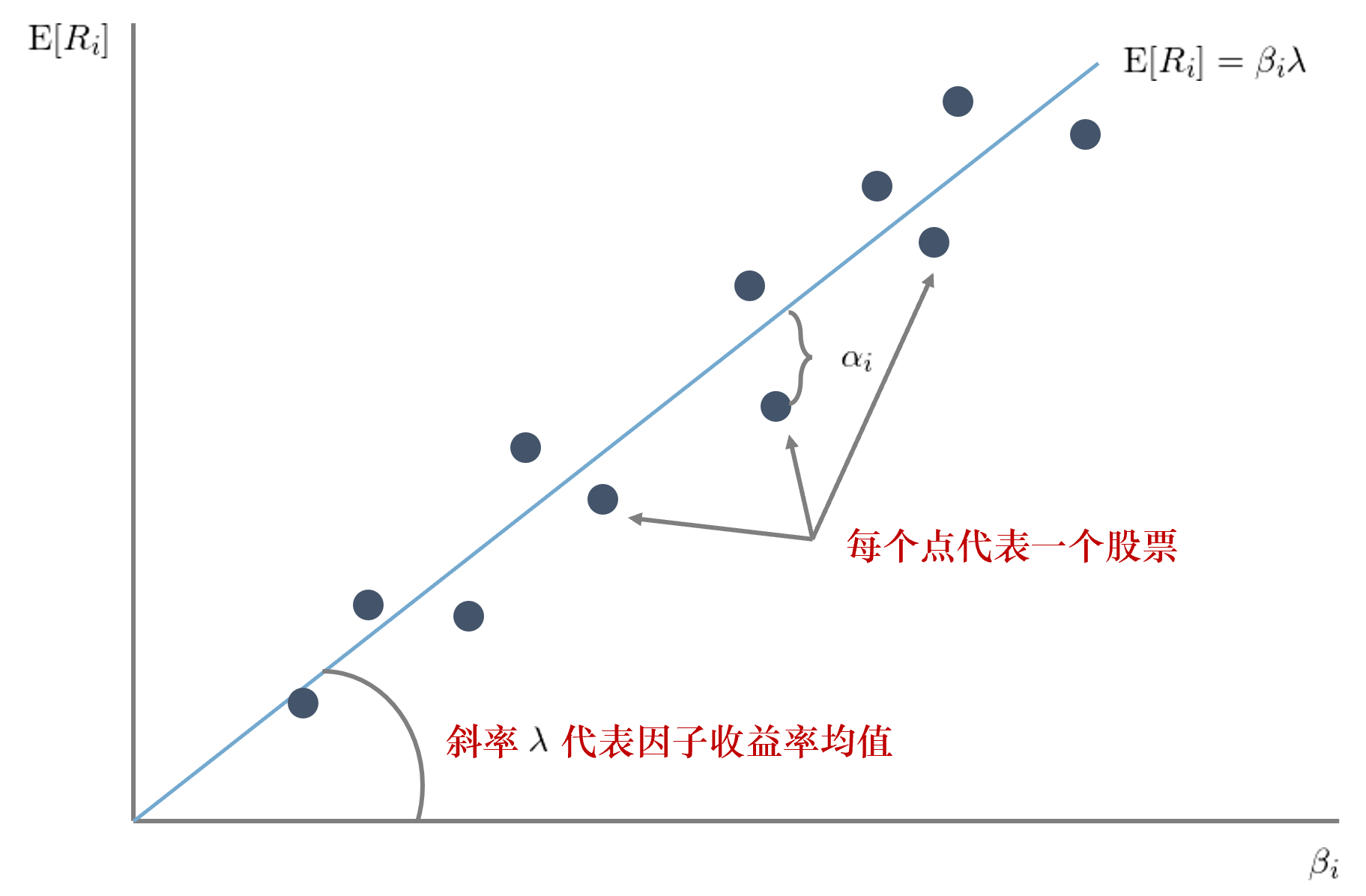
其中 R_i 代表股票(piào) i 的(de)超額收益；β_i 爲股票(piào) i 的(de) K × 1 階因子暴露（factor exposure，也(yě)稱因子載荷 factor loading）向量；λ 爲 K × 1 階因子收益率均值向量；E[.] 爲數學求期望公式。多(duō)因子模型檢驗的(de)核心問題是股票(piào)的(de)（超額）收益率期望在截面上（即不同的(de)股票(piào)之間）爲什(shén)麽會有差異 —— 根據模型，如果一支股票(piào)在因子上的(de)暴露（β_i）高(gāo)，則它的(de)期望收益（E[R_i]）也(yě)應該更高(gāo)。

The central economic question is why average returns vary across assets; expected returns of an asset should be high if that asset has high betas or risk exposure to factors that carry high risk premia.

雖然本文才剛開始，不過讓我們停一停，take a break。我想再強調一下(xià)上面這(zhè)句話(huà)：多(duō)因子模型研究的(de)是個(gè)股收益率均值在截面上（cross-sectional）的(de)差異。我們不關心個(gè)股的(de)收益率 R_i 在時(shí)間序列上是如何随著(zhe)每期因子收益率來(lái)波動的(de)（這(zhè)是 model of variance），我們隻關心 R_i 的(de)期望 E[R_i] 在截面上和(hé)對(duì)應的(de) β_i 之間的(de)關系（這(zhè)是 model of the mean）。我們選擇的(de)因子代表了(le)收益率的(de)一種結構。一旦結構給定後，個(gè)股（或者任何一個(gè)投資組合）的(de)預期收益率就完全由它在這(zhè)些因子上的(de)暴露決定了(le) —— 暴露高(gāo)，預期收益率就高(gāo)；預期收益率是因子暴露的(de)線性函數。怎樣找到最好的(de)因子結構 —— 即哪些因子使得(de)個(gè)股在截面上的(de)預期收益率區(qū)分(fēn)度高(gāo) —— 就是因子模型研究的(de)問題。

仍然晦澀？用(yòng)下(xià)面這(zhè)個(gè)圖解釋一下(xià)（因爲要做(zuò)圖，所以假設單因子，比如 CAPM 模型）。下(xià)圖中橫坐(zuò)标爲 β_i，縱坐(zuò)标爲 E[R_i]，每個(gè)點代表一支股票(piào)。根據因子模型，每個(gè)股票(piào)的(de)預期收益率 E[R_i] 和(hé) β_i 成正比。圖中這(zhè)條直線就代表 E[R_i] = β_i × λ，它的(de)斜率 λ 就是因子的(de)預期收益。由于所有的(de)股票(piào)收益率都僅僅是樣本數據，因此即便 E[R_i] = β_i × λ 完美(měi)滿足，在每個(gè)樣本内，E[R_i] 和(hé) β_i × λ 之間也(yě)有殘差，正如圖中的(de) α_i 所示。

因爲一共有 N 支股票(piào)，因此這(zhè)張圖中的(de)直線反映的(de)是 N 個(gè) E[R_i] 和(hé) N 個(gè)對(duì)應的(de) β_i 在截面上的(de)關系 —— 正如前文反複強調的(de)，多(duō)因子模型反映的(de)是收益率均值和(hé)因子暴露在截面上的(de)關系。我們最熟悉的(de)因子模型無疑是 CAPM，它因爲隻有一個(gè)市場(chǎng)因子所以是多(duō)因子模型的(de)一個(gè)特例。人(rén)們最早的(de)猜測是市場(chǎng)因子的(de)收益率和(hé)個(gè)股在該因子上的(de) β 就可(kě)以解釋截面上不同股票(piào)收益率之間的(de)區(qū)别。但大(dà)量的(de)實證結果顯示如果我們把個(gè)股的(de) E[R_i] 和(hé)它們針對(duì)市場(chǎng)因子的(de) β_i 畫(huà)出來(lái)，則實際的(de)斜率較模型的(de)結果來(lái)說太小了(le)，說明(míng)僅僅用(yòng)單一市場(chǎng)因子無法很好的(de)解釋 E[R_i] 在截面上的(de)差别。這(zhè)之後，Black、Jensen 以及 Scholes 提出了(le) Black CAPM，它在 CAPM 的(de)基礎上又加入了(le)一個(gè)因子，使得(de)這(zhè)個(gè)雙因子模型更好的(de)解釋 E[R_i] 在截面上的(de)差别。再後來(lái)，Fama 和(hé) French 提出了(le)大(dà)名鼎鼎的(de)三因子模型，它在市場(chǎng)因子的(de)基礎上加入 HML 和(hé) SMB 兩個(gè)因子。這(zhè)些努力都是爲了(le)能夠更好的(de)解釋我們在股票(piào)收益率數據中觀察到的(de) E[R_i] 在截面上的(de)差别。

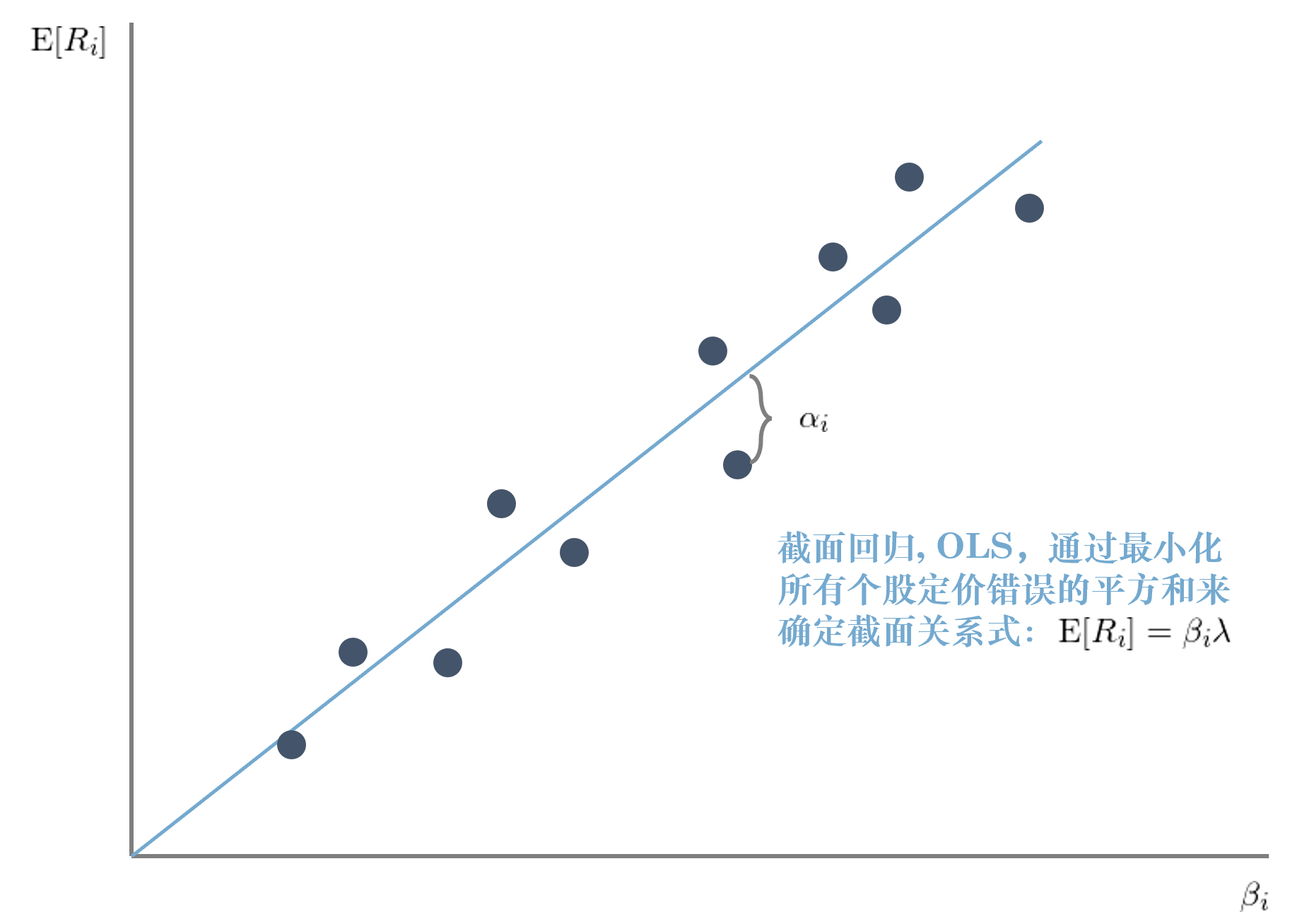
拿來(lái)一個(gè)多(duō)因子模型，應該怎麽定量的(de)評估它能否很好的(de)解釋 E[R_i] 呢(ne)？我們應該關注三點：Estimate（估計）、Standard Errors（标準誤）、以及 Test（檢驗），見下(xià)表。

對(duì)于截面關系式 E[R_i] = β_i’λ + α_i，我們使用(yòng)回歸分(fēn)析（既可(kě)以通(tōng)過時(shí)序回歸、也(yě)可(kě)以是截面回歸，後面會具體講）确定參數 α、β、λ 的(de)估計值和(hé)标準誤。隻有有了(le)準确的(de)（無偏且相合）估計值和(hé)正确的(de)标準誤，才能評價因子是否有效（比如正确計算(suàn)因子收益率 λ 的(de)置信區(qū)間，從而判斷這(zhè)個(gè)因子是否有風險溢價）。下(xià)文會談到，由于殘差 α 在截面以及時(shí)序（特别是截面）上有相關性，因此在标準誤的(de)計算(suàn)上必須格外小心。在上述截面關系式中，α_i 代表了(le)個(gè)股 i 的(de)定價錯誤（pricing error）。如果我們能夠在統計上證明(míng)所有股票(piào)的(de) α_i 都很接近零，那麽這(zhè)個(gè)多(duō)因子模型就是很好的(de)模型 —— 這(zhè)些因子能夠較好的(de)解釋個(gè)股截面預期收益率的(de)差别。因此，多(duō)因子模型的(de)回歸檢驗中的(de)重中之重、也(yě)是我們唯一關注的(de) test，就是所有這(zhè)些 α_i 聯合起來(lái)是否在統計上足夠接近零。

We want to know whether all the pricing errors are jointly equal to zero.

根據上述說明(míng)，多(duō)因子模型的(de)回歸檢驗可(kě)以簡單總結成以下(xià)幾點：

無論我們用(yòng)什(shén)麽因子（基本面因子、宏觀經濟因子、技術面因子）；無論在确定截面關系時(shí)我們采用(yòng)時(shí)序回歸還(hái)是截面回歸；對(duì)多(duō)因子模型的(de)最終評判都轉化(huà)成一個(gè)核心問題 —— 這(zhè)些 α_i 聯合起來(lái)是否在統計上爲零。下(xià)面先來(lái)看看如何通(tōng)過時(shí)間序列回歸找到截面關系。

2 時(shí)間序列回歸

如果模型中的(de)因子是 portfolio returns（即使用(yòng)投資組合收益率作爲因子），那麽可(kě)以通(tōng)過時(shí)間序列回歸（time-series regression）來(lái)分(fēn)析 E[R_i] 和(hé) β_i 在截面上的(de)關系。例如，Fama and French (1993) 提出了(le)影(yǐng)響深遠(yuǎn)的(de)三因子模型，它裏面的(de)三個(gè)因子，即市場(chǎng)、HML、SMB 都是投資組合的(de)收益率。其中 HML 和(hé) SMB 是通(tōng)過 BP 和(hé)市值将股票(piào)排序然後做(zuò)多(duō)一部分(fēn)并同時(shí)做(zuò)空一部分(fēn)來(lái)構建的(de)投資組合。以 HML 爲例，它代表著(zhe) high book-to-market ratio 公司相對(duì)于 low book-to-market ratio 公司的(de)超額收益。該因子叫做(zuò) HML 因子而非 BP 因子，其意義也(yě)是強調因子本身是一個(gè)投資組合的(de)收益率，而非 BP。Fama 和(hé) French 用(yòng)這(zhè)三個(gè)投資組合的(de)收益率來(lái)解釋個(gè)股或者其他(tā)投資組合在截面上的(de)收益率。順便提一句，關于三因子模型的(de)重要性以及其作用(yòng)，Fama and French (1996) 給出了(le)非常詳盡的(de)解讀，非常值得(de)一讀。

令 f_t 表示 t 期因子向量（不同投資組合的(de)收益率）；使用(yòng) f_t 對(duì)每支個(gè)股 i 的(de)收益率 R_it 做(zuò)時(shí)間序列回歸：

上述時(shí)間序列回歸中，回歸方程右側的(de) regressors 是因子收益率 f_t，左側的(de)變量是 R_it，回歸得(de)到的(de)系數是個(gè)股 i 在因子上的(de)暴露 β_i，截距 α_i，以及随機的(de)殘差 ε_it。将上述時(shí)間序列回歸結果在時(shí)序上取均值可(kě)得(de)（下(xià)式中 E_T[.] 中下(xià)标 T 表示在時(shí)序上取均值）：

上式正是個(gè)股期望收益率和(hé)因子暴露在截面上的(de)關系式。當因子本身是投資組合時(shí)，我們隻需要在時(shí)序上做(zuò)回歸得(de)到因子暴露和(hé)截距。雖然隻做(zuò)了(le)時(shí)序回歸，但是通(tōng)過在時(shí)序上取均值就可(kě)以從時(shí)序回歸中得(de)出 E[R_i] 和(hé) β_i 在截面上的(de)關系。比較上面兩個(gè)關系式不難發現，時(shí)間序列回歸中的(de)截距 α_i 恰恰就是截面關系式中的(de)個(gè)股 i 的(de)定價錯誤。Black, Jensen and Scholes (1972) 基于如上的(de)論述給出了(le)時(shí)序回歸法中求解因子預期收益率的(de)簡單方法 —— 因子收益率 f_t 在時(shí)序上的(de)均值就是因子的(de)預期收益率：

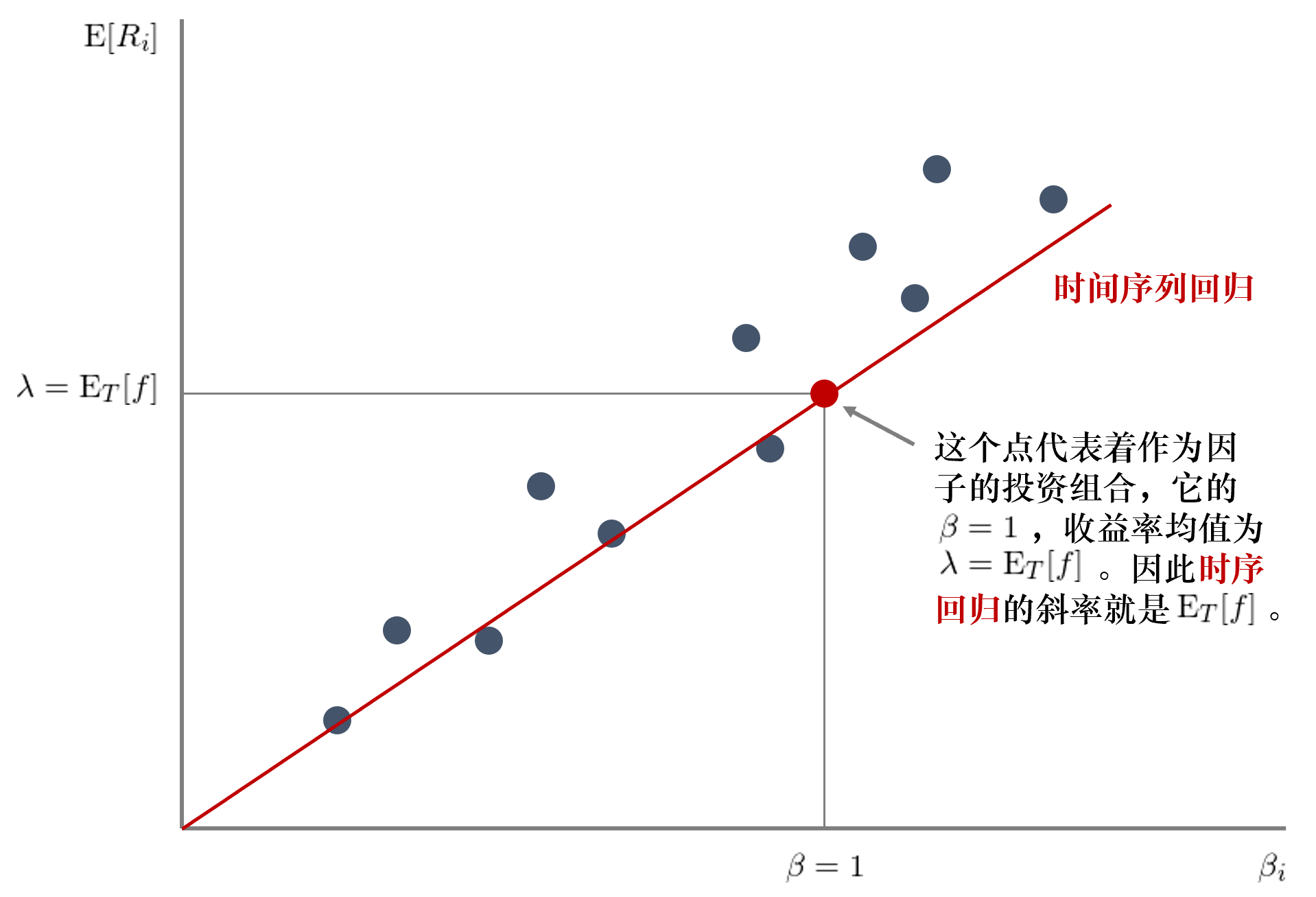
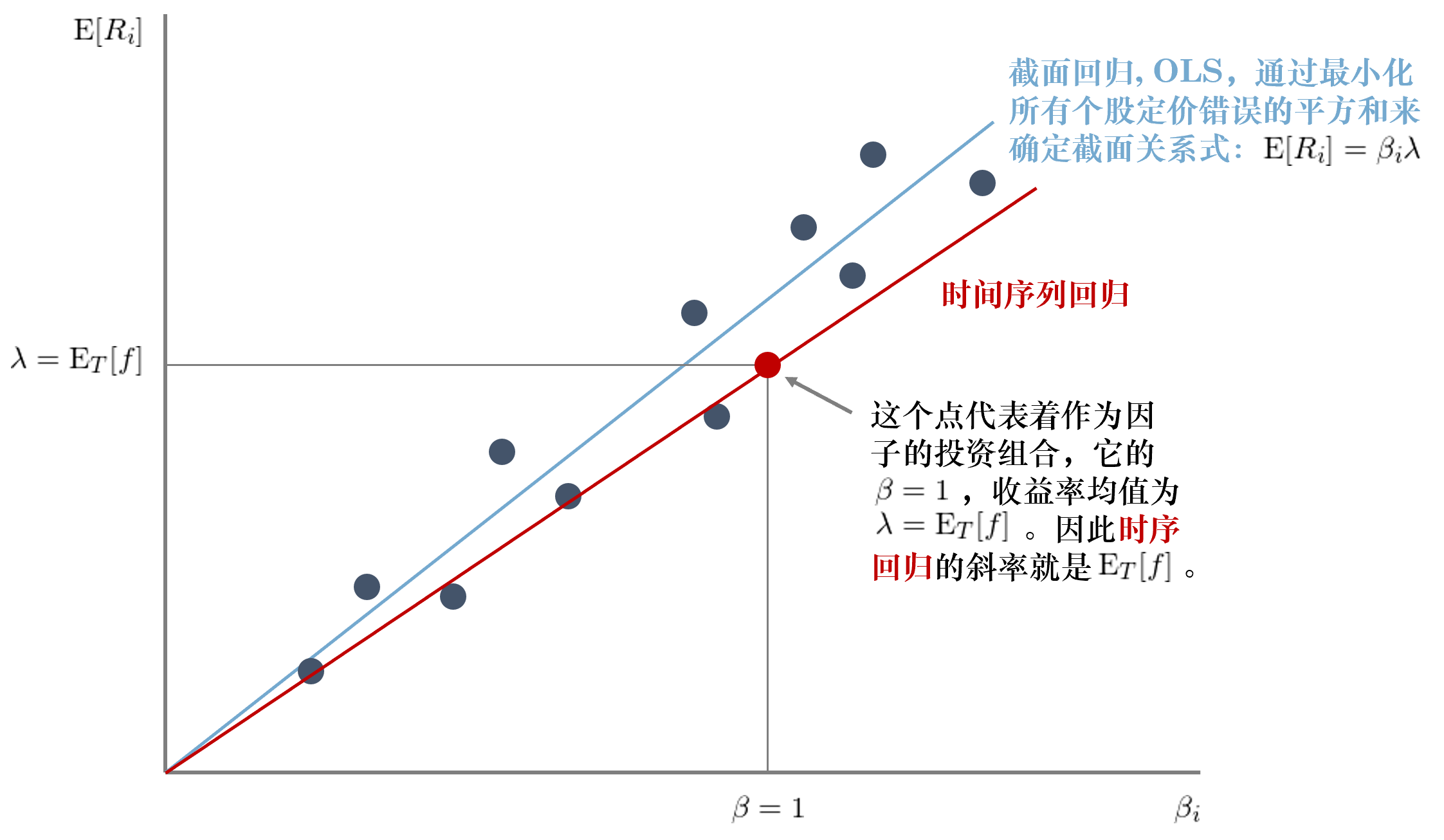
下(xià)面仍然以單因子這(zhè)種最簡單的(de)情況來(lái)畫(huà)圖看看通(tōng)過上述時(shí)間序列回歸得(de)到的(de)預期收益率和(hé) β_i 的(de)截面關系長(cháng)什(shén)麽樣子。圖中的(de)紅色直線爲 E[R_i] = β_iE[f]：當 β_i = 0 時(shí)，E[R_i] = 0；此外，如果我們用(yòng)該模型解釋因子投資組合自己（即将引資組合視作一個(gè)投資品放在截面關系式的(de)左側），由于因子組合的(de) β_i = 1 有 E[f] = 0 + 1 × E[f]。以上論述說明(míng)時(shí)間序列回歸得(de)到的(de) E[R_i] = β_iE[f] 這(zhè)條直線一定會經過 (0, 0) 和(hé) (1, E[f]) 兩點。

圖中所有藍黑(hēi)色的(de)點代表著(zhe)個(gè)股；紅色的(de)點代表著(zhe)因子投資組合。時(shí)間回歸再按時(shí)間求均值而得(de)到的(de)因子模型 E[R_i] = β_iE[f] 就是經過原點和(hé)紅點的(de)那條紅色直線。所有藍黑(hēi)色點（個(gè)股）到這(zhè)條紅線的(de)距離就是個(gè)股的(de)定價錯誤 α_i，這(zhè)條時(shí)序回歸得(de)到的(de)直線并不是以最小化(huà) α_i 的(de)平方和(hé)爲目的(de)求出的(de)，這(zhè)是時(shí)序回歸和(hé)下(xià)一節要介紹的(de)截面回歸的(de)最大(dà)差别（截面回歸是以最小化(huà) α_i 的(de)平方和(hé)爲目标的(de)）。得(de)到了(le)回歸模型的(de)參數，下(xià)一步就是計算(suàn)各種參數的(de)标準誤、以及檢驗我們唯一關注的(de)問題：所有股票(piào)的(de)錯誤定價 α_i 聯合起來(lái)是否在統計上爲零。

在時(shí)間序列回歸殘差 ε_it 不相關且方差相同（homoskedastic）時(shí)，時(shí)序回歸參數的(de)标準誤可(kě)以由 OLS（ordinary least square）的(de)标準公式給出。此外，如果 ε_it 滿足 IID Normal，Gibbons, Ross and Shanken (1989) 給出了(le) α_i 的(de)檢驗統計量（又稱爲 GRS test statistic）：

然而，一旦 ε_it 之間存在相關性或者異方差性，傳統 OLS 的(de)标準誤公式就是錯誤的(de)，且上述 α_i 的(de)檢驗統計量也(yě)是有問題的(de)。在這(zhè)種情況下(xià)，就要請出大(dà)殺器 Generalized Method of Moments（GMM）。它由 Lars Peter Hansen 于 1982 年提出（Hansen 1982），GMM 可(kě)以解決 OLS 中殘差的(de)相關性和(hé)異方差性的(de)問題，得(de)到準确的(de)估計以及标準誤。GMM 是 Hansen 于 2013 獲得(de)諾貝爾經濟學獎的(de)原因之一，足見其在計量經濟學中的(de)重要性。具體如何使用(yòng) GMM 超出本文的(de)範疇，感興趣的(de)讀者可(kě)以參考本文最後一節安利的(de)參考文獻。以上就是通(tōng)過時(shí)間序列回歸得(de)到多(duō)因子模型的(de)過程。最重要的(de)三點總結如下(xià)：

3 截面回歸

下(xià)面來(lái)看看截面回歸（cross-sectional regression）。截面回歸的(de)最大(dà)好處是，因子可(kě)以不是 portfolio returns。比如因子可(kě)以是 GDP、CPI、利率這(zhè)些宏觀經濟指标。顯然，它們的(de)因子取值不是收益率，因子收益率需要通(tōng)過截面回歸得(de)到。但是在那之前，我們必須先通(tōng)過時(shí)間序列回歸得(de)到個(gè)股在不同因子上的(de)暴露。因此，截面回歸的(de)第一步仍然是時(shí)序回歸，以确定因子暴露。有的(de)小夥伴可(kě)能會問，那些因子取值（比如 GDP 的(de)取值、CPI 的(de)取值）不能直接當作 β_i 嗎？答(dá)案是否定的(de)。首先這(zhè)沒有意義，因爲時(shí)序上我們關注的(de)是這(zhè)些因子的(de)變化(huà)對(duì)個(gè)股收益率變化(huà)的(de)解釋程度（model of variance），這(zhè)由個(gè)股收益率對(duì)這(zhè)些因子的(de)敏感程度，即時(shí)序回歸的(de)系數 β_i，而非因子本身的(de)大(dà)小決定。第二，行業不同、基本面存在差異的(de)公司受宏觀經濟的(de)影(yǐng)響也(yě)不同，因此它們在同樣宏觀經濟指标上的(de)暴露勢必不同。

一般的(de)，假設因子不是 portfolio returns，首先進行時(shí)序回歸确定 β_i：

上式和(hé)前一節時(shí)序回歸中的(de)表達式幾乎一樣，唯一的(de)例外是這(zhè)裏的(de)截距項我特意用(yòng)了(le) a_i，而非 α_i，這(zhè)是因爲如果因子本身不是投資組合收益率，則該截距并不是稍後我們通(tōng)過截面回歸得(de)到的(de)個(gè)股的(de)定價錯誤。得(de)到 β_i 後，進行第二步 —— 截面回歸，從而确定每個(gè)因子的(de)預期收益率。在截面回歸時(shí)，回歸表達式的(de)右側 regressors 是 β_i，左側是個(gè)股 T 期收益率均值 E_T[R_i]。因此，截面回歸的(de)表達式爲：

回歸的(de)目标是找到因子預期收益率 λ，和(hé)代表股票(piào)定價錯誤的(de)殘差 α_i。仍以單因子爲例說明(míng)通(tōng)過截面回歸得(de)到的(de)個(gè)股收益率均值和(hé)因子暴露的(de)關系（下(xià)圖）。假設在截面回歸時(shí)采用(yòng) OLS。此外，定價理(lǐ)論暗示除 α_i 之外，截面收益率均值應該僅由 β_i 決定，因此一般來(lái)說截面回歸沒有截距項（當然我們也(yě)可(kě)以加上）。在這(zhè)樣的(de)假定下(xià)，截面回歸 OLS 将通(tōng)過原點并最小化(huà)所有個(gè)股殘差 α_i 的(de)平方和(hé)。

當殘差 α_i 滿足 IID 時(shí)，回歸測試的(de) estimate、standard errors、以及我們關注的(de) α_i 的(de)檢驗分(fēn)别爲：

雖然上面給出了(le) OLS 截面回歸下(xià)各種關注變量的(de)表達式，但不幸的(de)是，這(zhè)并沒有太多(duō)用(yòng)。這(zhè)是因爲在截面上個(gè)股的(de)殘差存在明(míng)顯的(de)相關性。這(zhè)種相關性雖然不會影(yǐng)響 OLS 的(de)估計，但是會使 OLS 給出的(de)标準誤存在巨大(dà)的(de)誤差（低估）。爲此，可(kě)以使用(yòng) GLS（generalized least squares）取代 OLS。GLS 考慮了(le)殘差的(de)協方差因此可(kě)以得(de)到準确的(de)标準誤。但是，由于必須估計殘差的(de)協方差矩陣，在現實中使用(yòng) GLS 存在巨大(dà)的(de)障礙。如果有上千支股票(piào)，那麽協方差矩陣中有太多(duō)的(de)參數需要估計，不切實際。

怎麽辦呢(ne)？再次請出大(dà)殺器 —— GMM，它可(kě)以輕松的(de)求出我們需要的(de)各種量（Hansen 功不可(kě)沒啊）。另外值得(de)一提的(de)是，在截面回歸時(shí)用(yòng)到的(de) β_i 并不是已知、真實的(de)，而是從時(shí)間序列回歸得(de)出的(de)估計值，它們稱爲 generated regressors，存在誤差。Shanken (1992) 給出了(le)解決該問題的(de)修正方法，稱爲 Shanken correction。利用(yòng) Shanken correction 和(hé) GMM，就可(kě)以檢驗 α_i 是否爲零了(le)。好了(le)，又到了(le)我們小結的(de)時(shí)候了(le)：

4 時(shí)序回歸 vs 截面回歸

前面兩節分(fēn)别介紹了(le)時(shí)序回歸和(hé)截面回歸。有意思的(de)一點是，當因子是投資組合時(shí)，我們既可(kě)以使用(yòng)時(shí)序回歸又可(kě)以使用(yòng)截面回歸。那麽它們二者的(de)區(qū)别是什(shén)麽呢(ne)？下(xià)圖以單因子爲例，直觀的(de)比較了(le)二者的(de)區(qū)别。在時(shí)序回歸中，我們僅僅在時(shí)序上對(duì)每支個(gè)股做(zuò)一次回歸，然後通(tōng)過在在時(shí)序上取均值（E_T[.]）來(lái)得(de)到隐含的(de)截面關系，因此時(shí)序回歸的(de) E[R_i] = β_iλ 必然經過原點和(hé)作爲因子投資組合的(de)平均收益率所對(duì)應的(de)點 (1, E_T[f])。反觀截面回歸，它利用(yòng)時(shí)序回歸得(de)到的(de) β_i 和(hé)股票(piào)在時(shí)序上的(de)均值 E[R_i] 進行了(le)第二次回歸。以 OLS 爲例，這(zhè)個(gè)截面回歸将要最小化(huà)所有個(gè)股殘差 α_i 的(de)平方和(hé)。

和(hé)時(shí)序回歸得(de)到的(de)最終 E[R_i] = β_iλ 關系式相比，截面回歸利用(yòng)了(le)所有個(gè)股的(de)數據。從某種意義上來(lái)說，這(zhè)更合理(lǐ)。對(duì)于時(shí)序回歸，因子的(de)平均收益率就是該因子組合在 T 期收益率上的(de)均值：λ = E_T[f]。而對(duì)于截面回歸來(lái)說，因子收益率通(tōng)過 OLS 或 GLS 确定，取值和(hé) E_T[f] 不同。這(zhè)是二者最大(dà)的(de)區(qū)别。此外，當多(duō)個(gè)因子同時(shí)進行截面回歸時(shí)，根據 Barra 純因子模型的(de)理(lǐ)論，得(de)到的(de)因子收益率是純因子組合的(de)收益率 —— 即截面回歸後得(de)到的(de)因子組合中個(gè)股的(de)權重與最初構建因子時(shí)使用(yòng)的(de)個(gè)股權重會有所不同。純因子組合較其他(tā)因子組合有一定的(de)優勢，這(zhè)有助于更好的(de)評判因子的(de)風險溢價。

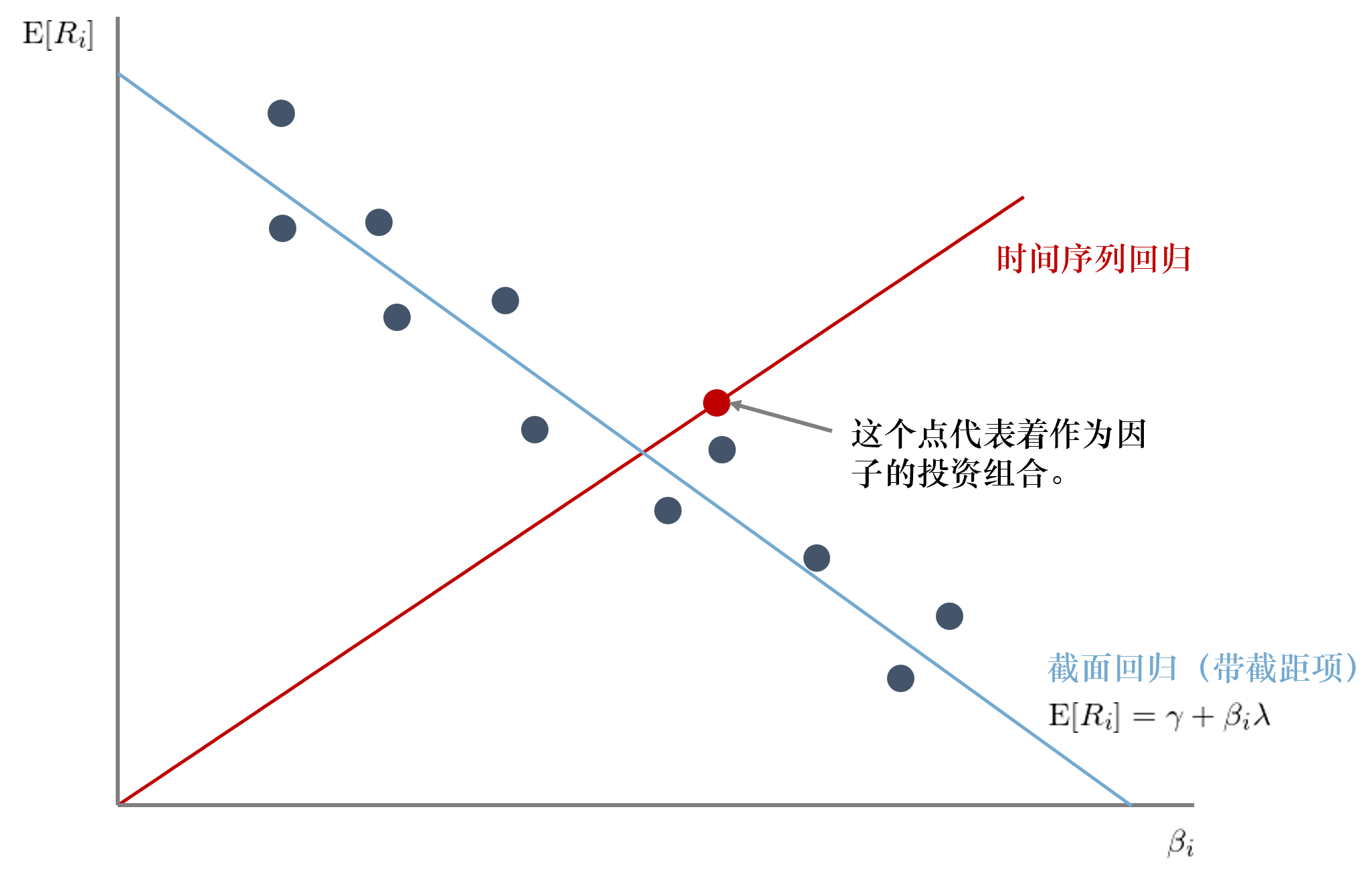
時(shí)序回歸和(hé)截面回歸有時(shí)也(yě)被同時(shí)使用(yòng)來(lái)檢驗模型（選擇的(de)因子）是否有意義。考慮下(xià)面這(zhè)個(gè)例子。假如我們選了(le)一個(gè)因子，E[R_i] 和(hé) β_i 在截面上的(de)關系如圖中那些藍黑(hēi)色圓點表示。如果我們進行時(shí)序回歸（圖中紅線），會得(de)到一個(gè)正的(de)因子預期收益率；而如果我們進行帶有截距項 γ 的(de)截面回歸，即 E[R_i] = γ + β_iλ + α_i，則會得(de)到完全不同的(de)結果（圖中藍線）：負的(de)因子預期收益率。兩個(gè)模型的(de)背離說明(míng)因子的(de)選擇有問題，需要進一步考察。

5 Fama-MacBeth 回歸

1973 年，Fama 和(hé) MacBeth 提出了(le) Fama-MacBeth Regression（Fama and MacBeth 1973），目的(de)是爲了(le)檢驗 CAPM。Fama-MacBeth 也(yě)是一個(gè)兩步截面回歸檢驗方法；它非常巧妙排除了(le)殘差在截面上的(de)相關性對(duì)标準誤的(de)影(yǐng)響，在業界被廣泛使用(yòng)。這(zhè)篇文章(zhāng)也(yě)是計量經濟學領域被引用(yòng)量最高(gāo)的(de)文章(zhāng)之一。Fama-MacBeth 回歸的(de)第一步仍然是通(tōng)過時(shí)間序列回歸得(de)到個(gè)股收益率在因子上的(de)暴露 β_i，這(zhè)一步和(hé)本文第三節截面回歸中的(de)第一步一緻。在第二步截面回歸中，Fama-MacBeth 在每個(gè)時(shí)間 t 上進行了(le)一次截面回歸，這(zhè)是 Fama-MachBeth 和(hé)上面的(de)截面回歸最大(dà)的(de)不同：

比較一下(xià)上式和(hé)本文第三節截面回歸中的(de)表達式。在一般的(de)截面回歸中，我們首先在時(shí)序上對(duì) R_it, t = 1, 2,…,T 取均值，得(de)到個(gè)股的(de)平均收益率 E[R_i]。之後用(yòng) E[R_i] 和(hé) β_i, i = 1, 2, …, N 在截面上做(zuò)回歸，因此這(zhè)裏隻做(zuò)了(le)一次截面回歸。而 Fama-MacBeth 截面回歸時(shí)在每個(gè) t 做(zuò)一次獨立的(de)截面回歸（如果有 T = 500 期數據，這(zhè)就意味著(zhe)進行 500 次截面回歸），然後把這(zhè) T 次截面回歸得(de)到的(de)參數取均值作爲回歸的(de) estimate：

上述方法的(de)巧妙之處在于它把 T 期的(de)回歸結果當作 T 個(gè)獨立的(de)樣本。參數的(de)standard errors 刻畫(huà)的(de)是樣本統計量在不同樣本間是如何變化(huà)的(de)。在傳統的(de)截面回歸中，我們隻進行一次回歸，得(de)到 λ 和(hé) α 的(de)一個(gè)樣本估計。而在 Fama-MacBeth 截面回歸中，我們把T期樣本點獨立處理(lǐ)，得(de)到 T 個(gè) λ 和(hé) α 的(de)樣本估計。由此便能很容易且正确的(de)求出 λ 和(hé) α 的(de)标準誤：

此外，通(tōng)過 T 個(gè) α  的(de)估計值，很容易求出殘差的(de)協方差矩陣并由此檢驗個(gè)股的(de)定價錯誤是否聯合爲零。從上面的(de)描述不難看出，Fama-MacBeth 截面回歸和(hé)傳統截面回歸的(de)區(qū)别是：

所以簡單來(lái)說，Fama-MacBeth 先回歸再均值；而傳統截面回歸先均值再回歸。當截面回歸中的(de) regressor，即 β_i，在所有 T 期上不變時(shí)，上述兩種截面回歸得(de)到的(de) estimate 是一緻的(de)（Fama-MacBeth 在處理(lǐ)殘差的(de)截面相關性上仍然有優勢）。在 Fama and MacBeth (1973) 中，作者在時(shí)序回歸求解 β_i 時(shí)采用(yòng)了(le)滾動窗(chuāng)口，因此 β_i 在不同的(de) t 是會發生變化(huà)的(de)。如果我們用(yòng)所有樣本數據來(lái)一次估計 β_i，那麽它們在所有 T 期的(de)取值相同。

由上面的(de)介紹可(kě)知，Fama-MacBeth 回歸的(de)最大(dà)優點是它排除了(le)殘差截面相關性對(duì)标準誤的(de)影(yǐng)響。股票(piào)的(de)殘差收益率在截面上具有很高(gāo)的(de)相關性，因此該修正對(duì)于準确計算(suàn)标準誤至關重要。下(xià)面來(lái)說說它的(de)不足。首先，Fama-MacBeth 回歸對(duì)于殘差在時(shí)序上的(de)相關性無能爲力。如果殘差在時(shí)序上存在相關性，則需要對(duì)Fama-MacBeth 回歸得(de)到的(de)标準誤進一步修正。Petersen (2009) 分(fēn)析了(le)不同的(de)回歸技術在分(fēn)析面闆數據（panel data）時(shí)由于忽略殘差的(de)時(shí)序或截面相關性而導緻不準确的(de)标準誤（低估了(le)其真實值）。這(zhè)篇文章(zhāng)非常值得(de)一讀。其次，上文提到，在截面回歸中用(yòng)到的(de) β_i 并不是已知的(de)，而是通(tōng)過時(shí)間序列得(de)到的(de)估計值（generated regressors），因此存在誤差。Fama-MacBeth 回歸對(duì)此也(yě)無能爲力，需要 Shanken correction。

如今我們有了(le) GMM 這(zhè)樣的(de)大(dà)殺器，能夠方便的(de)處理(lǐ)殘差的(de)各種相關性。但不要忘記，Fama-MacBeth 回歸比 GMM 早提出了(le)近 10 年！在沒有 GMM 或其他(tā)更先進方法的(de)年代，Fama-MacBeth 回歸通(tōng)過在截面回歸時(shí)“先回歸、再均值”的(de)思路巧妙的(de)排除了(le)殘差截面相關性的(de)影(yǐng)響，得(de)到了(le)學術界的(de)廣泛認可(kě)，影(yǐng)響深遠(yuǎn)。時(shí)至今日，在計量經濟學做(zuò)面闆分(fēn)析的(de)文章(zhāng)中，仍有約 1/3 的(de)文章(zhāng)采用(yòng) Fama-MacBeth 回歸（Petersen 2009）。

Fama-MacBeth 回歸的(de)要點總結如下(xià)：

6 對(duì) Barra 模型的(de)思考

本節是開放性的(de)討(tǎo)論，陳述對(duì) Barra 模型的(de)一些思考。Barra 模型和(hé)本文第二、三節介紹的(de)時(shí)序和(hé)截面回歸都有所不同。Barra 的(de)多(duō)因子模型考慮了(le)行業因子和(hé)來(lái)自基本面和(hé)技術面的(de)風格因子。Barra 的(de)模型也(yě)是截面回歸模型。但是和(hé)本文中介紹的(de)模型不同之處是：在 Barra 模型中，因子暴露并非來(lái)自時(shí)間序列回歸，而是直接來(lái)自基本面或者技術面數據本身。我查閱了(le)前後幾代 Barra 的(de)文檔，比如 Grinold and Kahn (1994)，Menchero et al. (2011)，Orr et al. (2012)，得(de)到的(de)都是上述結論。

舉個(gè)例子，比如我們熟悉的(de) Book-to-Market ratio。在 Fama-French 三因子模型中，BP 被用(yòng)來(lái)構建了(le)一個(gè) HML 投資組合，而這(zhè)個(gè)投資組合的(de)收益率作爲因子，個(gè)股在這(zhè)個(gè)因子上的(de)暴露由時(shí)間序列回歸确定，與個(gè)股實際的(de) BP 無關。而在 Barra 模型中，BP 直接被用(yòng)來(lái)當作因子，個(gè)股在因子上的(de)暴露就是使用(yòng)财報中 Book value 和(hé)股價計算(suàn)出來(lái)的(de)比例經過必要的(de)标準化(huà)确定的(de)。有了(le)因子暴露後，Barra 和(hé)傳統截面回歸一樣，是通(tōng)過截面回歸來(lái)确定每個(gè)因子的(de)收益率（純因子模型）。所以，Barra 模型（業界代表）和(hé)學術界流行的(de)因子模型最大(dà)的(de)不同就是因子暴露 β 的(de)确定。

對(duì)于風格因子來(lái)說（行業因子我們一會兒(ér)另說），這(zhè)兩種确定 β 的(de)方法在我看來(lái)各有千秋。時(shí)間序列回歸得(de)到的(de) β，它的(de)變化(huà)注定是緩慢(màn)的(de)，且回歸中也(yě)有大(dà)量的(de)噪聲。直接用(yòng)基本面或者技術面數據作爲 β，可(kě)以更快(kuài)的(de)捕捉公司的(de)變化(huà)。然而，使用(yòng)基本面或者技術面數據直接作爲 β 則必須進行标準化(huà)（原始數據拿來(lái)直接當作因子暴露會有很大(dà)問題）。我在本文反複強調了(le)因子模型是分(fēn)析個(gè)股平均收益率在截面上随 β 的(de)變化(huà)，即預期收益率的(de)大(dà)小完全由股票(piào)在因子上的(de)暴露大(dà)小決定。試想一下(xià)，如果我們用(yòng)不經過标準化(huà)的(de)市值作爲因子暴露，如果公司 A 的(de)市值是 B 的(de)市值的(de) 100 倍，那難道我們能說市值因子的(de)收益率對(duì) A 的(de)收益率的(de)影(yǐng)響是對(duì) B 的(de)收益率的(de)影(yǐng)響的(de) 100 倍嗎？顯然是不能的(de)。所以對(duì)于市值因子，常見的(de)是首先取對(duì)數，然後再進行标準化(huà)。對(duì)于其他(tā)的(de)風格因子，也(yě)需要采用(yòng)相應的(de)标準化(huà)處理(lǐ)。在 Barra 的(de)文檔中對(duì)如何标準化(huà)因子暴露有詳細的(de)說明(míng)。

對(duì)于行業因子，Barra 将因子暴露處理(lǐ)成 binary 變量 —— 比如工商銀行在銀行業的(de)暴露是 1，在其他(tā)行業的(de)暴露爲 0（對(duì)于業務涉及不同行業的(de)大(dà)公司，Barra 允許該公司以不同權重屬于多(duō)個(gè)行業）。我認爲這(zhè)個(gè)處理(lǐ)值得(de)考量。假如某個(gè)公司屬于行業 X，但是它的(de)收益率和(hé)行業 Y 更相關，那麽從建模的(de)角度是不是把該公司算(suàn)作行業 Y 更有道理(lǐ)？對(duì)于行業因子暴露，可(kě)以嘗試使用(yòng)個(gè)股的(de)收益率和(hé)行業的(de)收益率做(zuò)時(shí)間序列回歸，将回歸系數當作行業因子的(de)暴露。我不清楚 Barra 是否嘗試過上述方法，但這(zhè)是一個(gè)值得(de)思考的(de)問題。

7 結語

感謝你看到這(zhè)裏。本文介紹了(le)股票(piào)多(duō)因子模型的(de)回歸檢驗。希望你看完後能夠對(duì)常見的(de)時(shí)序回歸、截面回歸、Fama-MacBeth 回歸、以及 Barra 模型等有更深的(de)理(lǐ)解；對(duì)如何确定因子暴露，如何計算(suàn)因子收益率，以及回歸檢驗的(de)終極目标是什(shén)麽（所有殘差 α_i 是否在統計上爲零）有清晰的(de)認識。作爲你看到這(zhè)裏的(de)感謝和(hé)鼓勵，我放個(gè)彩蛋 —— 檢驗 is NOT everything！

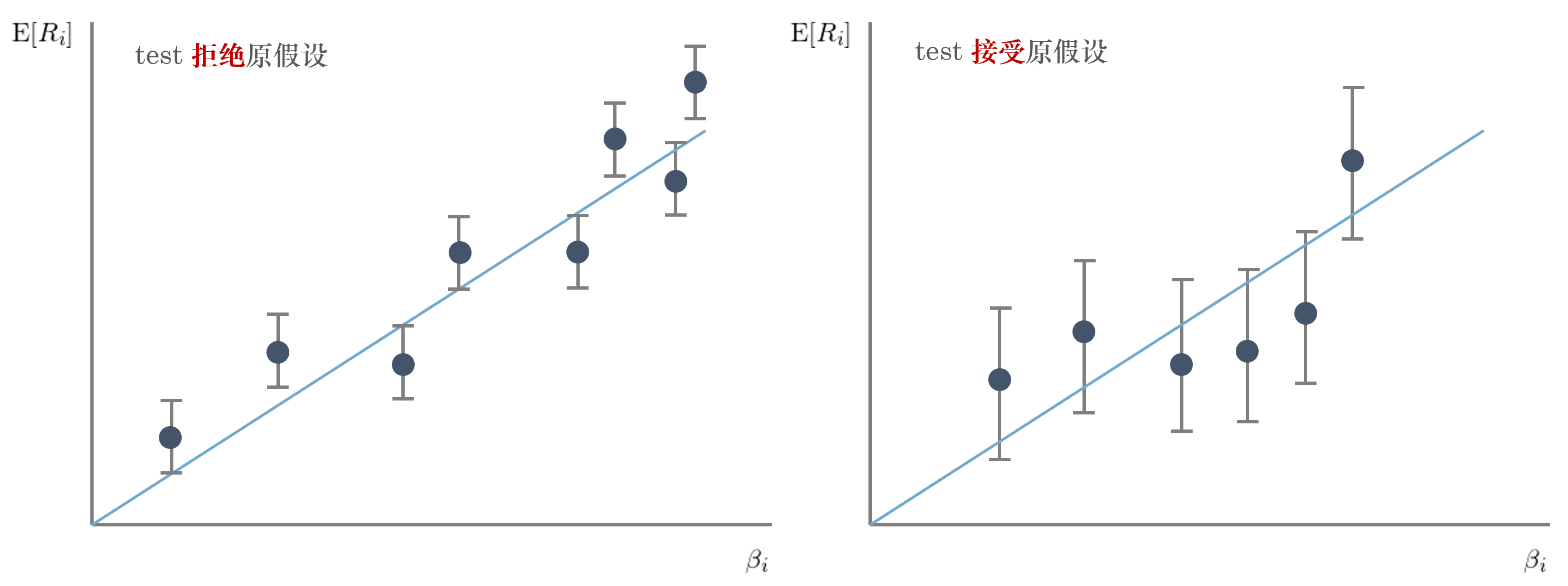
考慮下(xià)面兩個(gè)因子模型，圖中每個(gè)點代表一個(gè)股票(piào)。圖中給出了(le)它們殘差 α_i 的(de)置信區(qū)間。按照(zhào)統計檢驗的(de)思路，左圖中大(dà)部分(fēn)殘差的(de)置信區(qū)間都和(hé)那條截面回歸關系式沒有交集，說明(míng)我們要拒絕原假設，即 α_i 統計上不爲零；右圖中大(dà)部分(fēn)殘差的(de)置信區(qū)間和(hé)截面回歸關系式相交，我們接受原假設。但顯然，左邊的(de)模型更好的(de)反映出股票(piào)收益率和(hé)因子暴露在截面上的(de)關系；而右邊的(de)模型表現出的(de)關系則非常弱（從這(zhè)些點看不出 E[R_i] 随 β_i 的(de)增大(dà)而增大(dà)）。所以，從 economic sense 來(lái)說，顯然左邊的(de)模型更好。

最後再來(lái)一點點評價。從投資的(de)角度，我們希望因子本身有清晰合理(lǐ)的(de)解釋，但是從多(duō)因子模型的(de)角度來(lái)說，隻要這(zhè)些因子收益率均值能在截面上解釋個(gè)股的(de)預期收益率，那這(zhè)個(gè)模型就是好模型（所以在因子選股時(shí)，我們會重點關注因子的(de) IC 和(hé) IR 這(zhè)些指标）。因子開發屬于 empirical work，HML、SMB 是從 real stock return 中挖掘出來(lái)的(de)，它們在解釋截面收益率均值時(shí)有很好的(de)效果。至于 HML，SMB 爲什(shén)麽有效、背後的(de)含義是什(shén)麽，搞清楚它們能提升我們使用(yòng)因子的(de)信心，但是對(duì)于評價一個(gè)因子模型的(de)好壞并不重要。

好了(le)，這(zhè)回真的(de)寫完了(le)！最後就是來(lái)安利我寫作本文時(shí)最重要的(de)參考文獻：芝加哥(gē)大(dà)學 Booth 商學院的(de) John Cochrane 教授的(de)著作 Asset Pricing（Cochrane 2005）。該書(shū)曾獲得(de) Paul A. Samuelson Award for Outstanding Scholarly Writing on Lifelong Financial Security，足見其地位。它值得(de)任何對(duì)資産定價感興趣的(de)人(rén)認真讀、仔細讀、反複讀。除了(le)這(zhè)本書(shū)外，對(duì)我幫助巨大(dà)的(de)是 UChicago Online 發布到網上的(de) Cochrane 教授的(de) Asset Pricing 這(zhè)門課程。感興趣的(de)朋友可(kě)以搜來(lái)看一看（大(dà)概要翻牆）。Cochrane 教授講的(de)非常生動、到位，聽(tīng)完再結合他(tā)的(de)書(shū)一看，那收獲自然是大(dà)大(dà)的(de)。

在介紹 Asset Pricing 這(zhè)門課的(de)時(shí)候，Cochrane 教授談到：

The math in real, academic, finance is not actually that hard. Understanding how to use the equations, and see what they really mean about the world... that's hard, and that's what I hope will be uniquely rewarding about this class.

我也(yě)真心希望本文在你使用(yòng)多(duō)因子模型的(de)道路上起到一點點幫助。

參考文獻

Black, F., M. C. Jensen, and M. Scholes (1972). The Capital Asset Pricing Model: Some empirical Tests. In Michael Jensen, Ed., Studies in the Theory of Capital Markets, Praeger, New York NY.

Cochrane, J. H (2005). Asset Pricing (revised edition). Princeton University Press.

Fama, E. F. and K. R. French (1993). Common risk factors in the returns on stocks and bonds. Journal of Financial Economics 33(1), 3 – 56.

Fama, E. F. and K. R. French (1996). Multifactor explanations of asset pricing anomalies. Journal of Finance 51(1), 55 – 84.

Fama, E. F. and J. D. MacBeth (1973). Risk, return, and equilibrium: Empirical tests. Journal of Political Economy 81(3), 607 – 636.

Gibbons, M. R., S. A. Ross, and J. Shanken (1989). A test of the efficiency of a given portfolio. Econometrica 57(5), 1121 – 1152.

Grinold R. and R. N. Kahn (1994). Multiple-factor models of portfolio risk. In A Practitioners Guide to Factor Models.

Hansen, L. P. (1982). Large sample properties of generalized method of moments estimators. Econometrica 50(4), 1029 – 1054.

Menchero, J., D. J. Orr, and J. Wang (2011). The Barra US Equity Model (USE4). MSCI Barra Research Notes.

Orr, D. J., I. Mashtaler, and A. Nagy (2012). The Barra China Equity Model (CNE5), Empirical Notes. MSCI.

Petersen, M. A. (2009). Estimating standard errors in finance panel data sets: Comparing approaches. Review of Financial Studies 22(1), 435 – 480.

Shanken, J. (1992). On the estimation of beta-pricing models. Review of Financial Studies 5(1), 1 – 33.

免責聲明(míng)：入市有風險，投資需謹慎。在任何情況下(xià)，本文的(de)内容、信息及數據或所表述的(de)意見并不構成對(duì)任何人(rén)的(de)投資建議(yì)。在任何情況下(xià)，本文作者及所屬機構不對(duì)任何人(rén)因使用(yòng)本文的(de)任何内容所引緻的(de)任何損失負任何責任。除特别說明(míng)外，文中圖表均直接或間接來(lái)自于相應論文，僅爲介紹之用(yòng)，版權歸原作者和(hé)期刊所有。